ABSTRACCIÓN INICIAL REVISITADA Victor M. Ponce y Luis Magallon
|
|
Se revisa el concepto de abstracción inicial en el método del número de la curva del NRCS, a la luz de los resultados demostrablemente diferentes obtenidos por los modelos en actual uso (SWMM y HEC-HMS). El método del número de la curva no está distribuido en el tiempo, pero se ha utilizado en la práctica como un modelo distribuido, más allá del alcance de su desarrollo original. Esto ha llevado a varias formas de tomar en cuenta la abstracción inicial. Existe una necesidad urgente de revisar el concepto y desarrollar un nuevo estándar, para que los diversos modelos conduzcan a resultados similares. |
El concepto de abstracción inicial ha evolucionado
desde su introducción en la década de 1950 como
parte del método del número de la curva del NRCS
(Ponce, 2014).
Varias interpretaciones están en uso actual, lo
que ha desafiado la estandarización. Los modelos
hidrológicos como SWMM y HEC-HMS aplican el concepto
de diferentes maneras, lo que da como resultado
diferentes soluciones. Por lo
tanto, se ha vuelto
necesario revisar y aclarar
el concepto de abstracción
inicial en el método del número
de la curva,
con la esperanza de que en el futuro,
cuando el método
se use junto con SWMM y HEC-HMS, el
hidrograma calculado
sea esencialmente el mismo.
El concepto de abstracción inicial se originó con
el método del número de la curva de escorrentía
(RCN) del NRCS, desarrollado por el Servicio
de Conservación de Recursos Naturales del USDA
(anteriormente Servicio de Conservación de Suelos, o SCS)
en la década de 1950, y documentado en
el Manual Nacional
de Ingeniería: Parte 630 - Hidrología.
Para una profundidad de precipitación P y
el número de curva de escorrentía CN,
la abstracción inicial Ia es
la fracción inicial de profundidad de la
precipitación después de la cual comienza la
escorrentía.
Victor Mockus, el desarrollador principal
del método RCN, creía que para cualquier
caso, la cantidad de abstracción inicial
era, para todos los propósitos prácticos,
intratable. Para sortear el problema, Mockus
propuso graficar
Como Mockus le dijo a Ponce en la ahora famosa
entrevista (Ponce, 1996),
sus superiores rechazaron la idea, pues
creían que un componente de abstracción inicial
tenía que ser parte del naciente método RCN.
Entonces, la ecuación numérica de la curva
de escorrentía original desarrollada por Mockus es:
P - Q Q en la cual
S = almacenamiento potencial, con todas
las variables dadas en unidades de profundidad.
La abstracción inicial Ia
se sustrajo de la profundidad de
la tormenta P para obtener:
P - Ia - Q Q
Para simplificar el método, Mockus expresó la
retención potencial S en términos
de un más manejable
1000
en el cual CN es un número adimensional
limitado en el rango 1 ≤ CN ≤ 100,
y todos los demás términos
de la
Para que el método siguiera siendo
práctico, con un solo parámetro (CN),
la abstracción inicial tenía que estar
relacionada con el almacenamiento S.
Después de un análisis detallado, se adoptó la
siguiente relación:
Ia = λ S
en la cual λ = parámetro de abstracción inicial.
Al inicio del método, el valor de
En la actualidad (2020), el NRCS no ha tomado
aún una decisión sobre si mantener o cambiar
el valor de λ. Dado que el
conjunto actual de CN se desarrolló junto con
En el tiempo transcurrido desde su desarrollo original,
el método del número de la curva NRCS se ha
convertido en un estándar
Mockus señaló que el método no
pretendía predecir
la tasa de infiltración,
sino el volumen total de infiltración para un
evento de tormenta dado (Ponce, 1996).
Dados P (en pulgadas) y una estimación
de CN, el volumen de escorrentía Q (en pulgadas) es
(Ponce, 2014):
[ CN ( P + 2 ) - 200 ] 2
Como se propuso originalmente, el método NRCS RCN se agrupa
efectivamente en el tiempo, proporcionando una estimación de
la escorrentía de la tormenta Q (pulgadas),
dada la profundidad
de la tormenta P (pulgadas)
y un valor de CN apropiado, independientemente
de la duración de la tormenta, la cual no se tiene en cuenta de manera
explícita. Mockus afirmó que el dato de apoyo utilizado
en el desarrollo del método fue la precipitación
diaria, debido a que este tipo de datos era el único
disponible en grandes cantidades
(Ponce, 1996).
En la práctica, esto significa que el método
RCN debería
funcionar mejor cuando la duración de la tormenta es
cercana a un (1) día, aunque en repetidas aplicaciones
éste no ha sido necesariamente el caso
(NRCS, 1986).
La definición correcta de abstracción
inicial en el método NRCS RCN
se deriva del desarrollo original del método:
"Para una profundidad de tormenta P
y número de curva CN,
la abstracción inicial Ia
es la fracción de la profundidad de la tormenta
después de la cual comienza la escorrentía".
Hay que tener en cuenta que en
Según el método RCN, la escorrentía Q
es una función de la profundidad de la tormenta P
y el número de curva CN, independientemente de la
duración de la tormenta. Por lo tanto, para
un número de curva CN dado, el
almacenamiento S y la abstracción
inicial Ia son constantes. Al
igual que P, S, y Q, la
abstracción inicial Ia es un volumen,
interpretado como una fracción de la profundidad de la
tormenta, distribuida uniformemente para la duración de
la tormenta dada y la cuenca siendo considerada.
Aquí arguimos que si CN y S
no tienen en cuenta ni la tasa de infiltración ni la
duración de la tormenta, tampoco debería hacerlo
la abstracción inicial Ia. Partiendo de
esta premisa, parece injustificado situar la
abstracción inicial al comienzo de la tormenta.
Observamos que el método RCN está agrupado en
el tiempo, originalmente desarrollado para
tormentas de 24 horas de duración, y posteriormente
extendido a modo de práctica a tormentas de menor
duración.
Dado tr = duración de la tormenta,
tc =
tiempo de concentración,
y Pe = precipitación efectiva,
la distribución de la abstracción total (P - Q)
(es decir, las pérdidas totales) de manera
uniforme en el tiempo produce una intensidad
de lluvia efectiva constante (Ie
= Pe/tr). Para
tr ≥ tc,
este procedimiento conduce a la concentración de
escorrentía, con caudal pico Qp1
(Ponce, 2014):
Qp1 = Ie A
Por el contrario, si la abstracción inicial se contabiliza al
comienzo de la tormenta, la abstracción
total (P - Q) no se distribuye
uniformemente en el tiempo. Por lo tanto, para
conservar la masa a lo largo de la duración de la
tormenta, la concentración de escorrentía debe
alcanzarse en un caudal
máximo Qp2, en el cual:
Qp2 > Qp1
con diferencias significativas entre los dos enfoques.
La Figura 1 muestra un ejemplo típico de la diferencia
en los caudales máximos (Magallon y Ponce, 2015). El
modelo
Queda la pregunta de cuál de los enfoques para
la abstracción de precipitación utilizando
el método del
número de curva de escorrentía es más realista o
más apropiado. Esto da como resultado diferencias
sustanciales en las propiedades hidrográficas
(Magallon and Ponce, 2015).
Fig. 1 Comparación de hidrogramas para
tres modelos de flujo superficial, utilizando
Se revisa el concepto de abstracción inicial
en el método del número de la curva de
escorrentía del NRCS, a la luz de los resultados
demostrablemente diferentes obtenidos por los
modelos hidrológicos en uso actual
(SWMM y
BIBLIOGRAFÍA
Hawkins, R. H., R. Jiang, D. E. Woodward, A. T.
Hjelmfelt, y J. E. VanMullen. 2002.
Runoff curve
number method: Examination of the initial
abstraction ratio. Proceedings of the Second Federal Interagency
Hydrologic Modeling Conference, Las Vegas, Nevada.
Magallon, L., y V. M. Ponce. 2015. Comparison between overland flow models.
Publicación en linea.
Ponce, V. M. 1996. Notas de mi conversación con Vic Mockus. Publicación en linea.
Ponce, V. M. 2014. Engineering Hydrology, Principles and Practices. Publicación en linea.
Ponce, V. M., y R. H. Hawkins. 1996.
Runoff curve number: Has it reached maturity?
ASCE Journal of Hydrologic Engineering, Vol. 1, No. 1, January, 11-19.
USDA Natural Resources Conservation Service. 1986.
Urban Hydrology for Small Watersheds.
USDA Natural Resources Conservation Service. 2015.
National Engineering Handbook: Part 630 - Hydrology.
_______ = ______
S P
(1)
___________ = _________
S P - Ia
(2)
S = _________ - 10
CN
(3) (4)
Q = ___________________________
CN [ CN ( P - 8 ) + 800 ]
(5)
(6) (7)
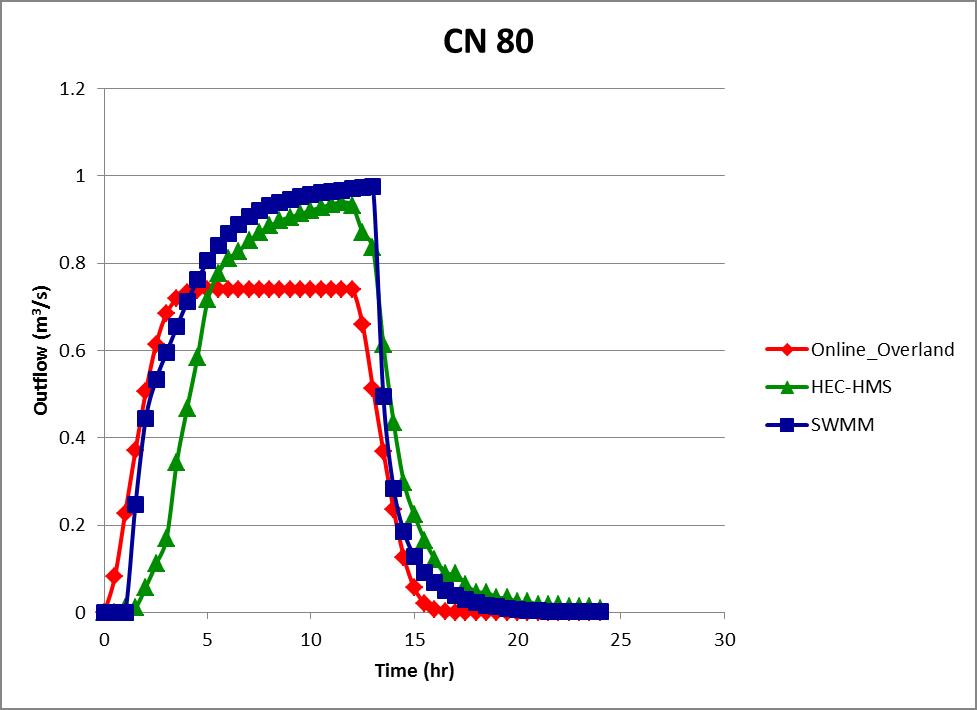
el número de curva de escorrentía NRCS como método de abstracción.