APLICACIÓN DEL HIDROGRAMA UNITARIO ADIMENSIONAL USANDO DATOS DE CUENCAS DE CALIFORNIA
Luis Gustavo Ariza Trelles
1. INTRODUCCIÓN
1.1 Introducción El concepto de hidrograma unitario está bien establecido en la investigación y práctica de la ingeniería hidrológica. El hidrograma unitario se define como el hidrograma producido por una profundidad unitaria de escorrentía uniformemente distribuida sobre toda la cuenca y con una duración unitaria específica. El concepto se ha utilizado desde la década de 1930 para la simulación de flujos de inundación en todo el mundo (Sherman, 1932). El hidrograma unitario adimensional general (HUAG), fue desarrollado por Ponce (2009a, 2009b), es una formulación adimensional del hidrograma unitario. El HUAG asocia efectivamente la técnica de convolución (del hidrograma unitario) con el modelo de cascada de reservorios lineales (CRL), originalmente debido a Nash (1957). El modelo CRL constituye de componente de tránsito de varios modelos hidrológicos que se han desarrollado desde entonces alrededor de todo el mundo, en particular el modelo SSARR (U.S. Army Engineer North Pacific Division, 1972). Este estudio intentó validar el modelo HUAG utilizando información de cuencas de California. La información geográfica y los datos de precipitación-escorrentía del Estado de California están disponibles en la web; esto facilitó la recopilación y análisis. Los mapas de elevación digital (DEM) están disponibles en las plataformas virtuales del USGS como Earth Explorer y Alaska Satellite Facility. La información de precipitación está disponible en la plataforma virtual del NOAA como National Centers for Environmental Information. La información de descargas está disponible en la plataforma virtual del USGS como National Water Information System. Para el estudio se seleccionaron y analizaron diez (10) cuencas de California. Con la finalidad de estudiar la difusión del hidrograma unitario, las cuencas abarcaron un amplio rango de valores de parámetros geomorfológicos (área de drenaje, pendiente promedio superficial del terreno, y pendiente del canal principal). Los análisis conceptuales y estadísticos fueron utilizados para desarrollar una metodología de predicción de hidrogramas unitarios en base a la geomorfología local/regional de la cuenca. Dada la perspectiva del calentamiento global y su efecto de aumento en los flujos de inundación, la oportunidad de este esfuerzo no puede ser exagerado. 1.2 Objectivos Los objetivos del estudio son: General
Específicos:
1.3 Alcances Este estudio abarcó el desarrollo de un modelo predictivo para calcular hidrogramas unitarios en base a la geomorfología local/regional. El esfuerzo enfatizado en esta metodología es conceptual, basada en el tiempo-prueba de la teoría de la cascada de reservorios lineales. El enfoque central del hidrograma unitario adimensional general (HUAG) como teoría unificadora, realza el ejercicio de la validación.
2. TEORÍA
2.1 Hidrograma unitario Durante el siglo pasado, el hidrograma unitario (HU) se ha utilizado como una metodología para generar flujos de inundación para cuencas de tamaño mediano a grande (Ponce, V. M., 1989), (Ponce, V. M., 2014a). En 1930, el Comité de Inundaciones de la Sociedad de Ingenieros Civiles de Boston, después de un estudio de hidrogramas de inundación en Nueva Inglaterra, concluyó en la siguiente referencia (Hoyt, 1936, p. 123):
Esta declaración puede ser interpretada de la siguiente manera: Para una cuenca de determinada área de drenaje A, dándole un simple evento de precipitación de profundidad efectiva d y una duración tr, que cubra su área entera, el volumen de escorrentía Vr y consecuentemente el pico del flujo Qp, son proporcionales a la intensidad de precipitación efectiva d/tr. En otras palabras, la respuesta del hidrograma (Q) es lineal con respecto a la intensidad y, por lo tanto, independiente del tiempo base Tb. Sherman (1932) elaboró sobre este concepto el desarrollo de estudios del hidrograma unitario para inundación en grandes cuencas. Normalmente, se entiende que la palabra unidad se refiere a una profundidad unitaria de lluvia efectiva o escorrentía. Sin embargo, debe observarse que Sherman primero utilizó la palabra para describir una unidad de profundidad de escorrentía (1 cm o 1 in.) durante un incremento de tiempo unitario, es decir, un incremento indivisible. La unidad de incremento de tiempo puede ser 1 h, 3 h, 6 h, 12 h, 24 h, o cualquier otro tipo duración (Ponce, V. M., 2014a).
El hidrograma unitario se define como el hidrograma producido por una unidad de profundidad de escorrentía distribuida uniformemente sobre una cuenca entera y que tiene una duración unitaria de tiempo específico.
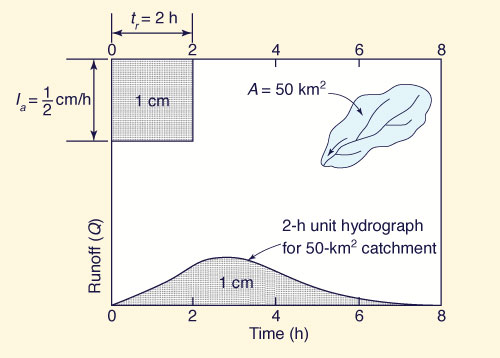
Para ilustrar el concepto del hidrograma unitario, supongamos que cierta tormenta produce 1 cm de escorrentía y cubre una cuenca de 50 km2 durante un periodo de tiempo de 2 h.
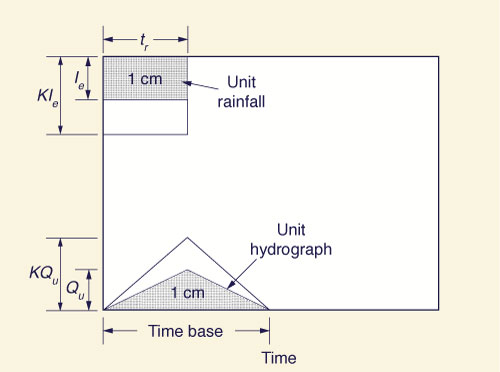
Dado un hidrograma unitario, un hidrograma para otra unidad de profundidad de escorrentía puede obtenerse simplemente multiplicando las ordenadas del hidrograma unitario por la profundidad de escorrentía indicada (linealidad), como se muestra en la Fig. 2.2 (a).
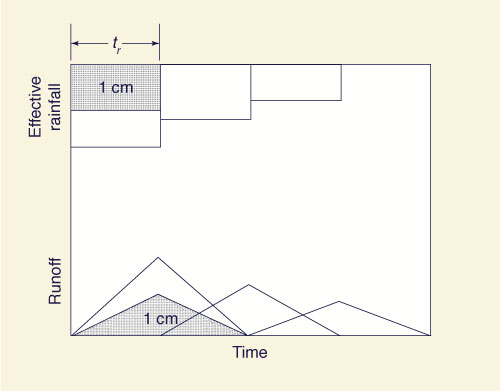
El tiempo base de todos los hidrogramas obtenidos de esta manera es igual a la del hidrograma unitario. Por lo tanto, el procedimiento puede utilizarse para calcular hidrogramas producidos por una tormenta consistente o una serie de profundidades de escorrentía, cada retardo en tiempo incrementa la duración del hidrograma unitario, como se muestra en Fig. 2.2 (b).
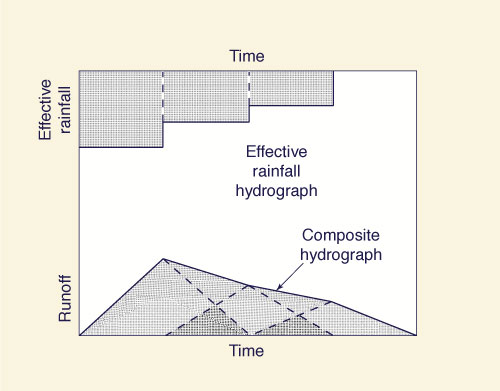
La sumatoria de las ordenadas correspondientes de los hidrogramas (superposición) permite el cálculo del hidrograma compuesto, como se muestra en la Fig. 2.2 (c). El procedimiento mostrado en la Fig. 2.2 es referente a la convolución de un hidrograma unitario con un patrón de tormenta efectiva (hietograma). En esencia, el procedimiento equivale a decir que las ordenadas del hidrograma compuesto son una combinación lineal de las ordenadas del hidrograma unitario.
La asunción de linealidad ha sido largamente considerada como una de las limitaciones de la teoría del hidrograma unitario. En la naturaleza, es improbable que la respuesta de una cuenca siempre sea una función lineal. Por una parte, la descarga y la velocidad media son funciones no lineales de la profundidad de flujo y almacenamiento. En la práctica, sin embargo, la asunción lineal proporciona un medio conveniente para calcular la respuesta de la escorrentía sin asociar complejidades con el análisis no lineal. El límite superior de aplicabilidad del hidrograma unitario no está muy bien definido. (Sherman, 1932) lo utilizó en conexión con cuencas que varían de 1300 a 8000 km2. (Linsley, Kohler, & y Paulhus, 1962) mencionan un límite superior de 5000 km2 para preservar la precisión. Más recientemente, el hidrograma unitario se ha relacionado con el concepto de cuenca media, es decir, mayor a 2.5 km2 y menor de 250 km2. Esto ciertamente no impide que la técnica del hidrograma unitario sea aplicable a cuencas mayores de 250 km2, aunque es probable que la precisión tienda a disminuir con un incremento en el tamaño de la cuenca (Ponce, 2014a). 2.2 Tránsito de almacenamiento y reservorios lineales Como se muestra en la Sección 2.3, los conceptos del hidrograma unitario y la cascada de reservorios lineales están intrínsecamente conectados. La cascada es efectivamente una serie de reservorios lineales, y esta última es una manera de determinar el tránsito de almacenamiento. Por lo tanto, esta sección aborda el tránsito de almacenamiento y reservorios lineales. Las técnicas para tránsito de almacenamiento son invariablemente basadas en la ecuación diferencial de almacenamiento de agua. Esta ecuación es fundamentada sobre el principio de conservación de masa, que establece que el cambio en el flujo por unidad de longitud en un volumen de control es equilibrado por un cambio de área de flujo por unidad de tiempo. En forma diferencialmente parcial se puede expresar de la siguiente manera:
En la cual Q = rango de caudal, A = área de flujo, x = espacio (longitud), y t = tiempo. La ecuación diferencial de almacenamiento se obtiene agrupando variaciones espaciales. Para este propósito, la Ec. 2-1 es expresada en incrementos finitos:
En la cual ΔQ = O - I, donde O = flujo de salida, e I = flujo de ingreso; y ΔS = ΔA Δx , donde
En la cual flujo de ingreso, flujo de salida, y rango de cambio de almacenamiento son expresados en unidades de L3T -1. Además, la Ec. 2-3 puede ser expresado de forma diferencial, originando la ecuación diferencial de almacenamiento.
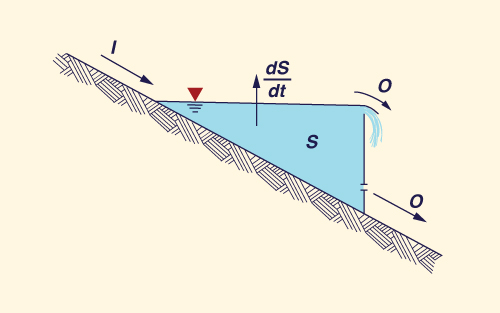
La Ecuación 2-4 implica que cualquier diferencia entre el flujo de ingreso y el flujo de salida este equilibrado por un cambio de almacenamiento en el tiempo (Fig. 2.3). En una típica aplicación de tránsito de reservorios, el hidrograma de flujo de ingreso (condición de borde aguas arriba), el almacenamiento y flujo de salida inicial (condiciones iniciales), y las características físicas y operacionales del reservorio son conocidas. Por lo tanto, el objetivo es calcular el hidrograma del flujo de salida para la condición inicial, la condición de borde aguas arriba, las características del reservorio, y sus reglas operacionales.
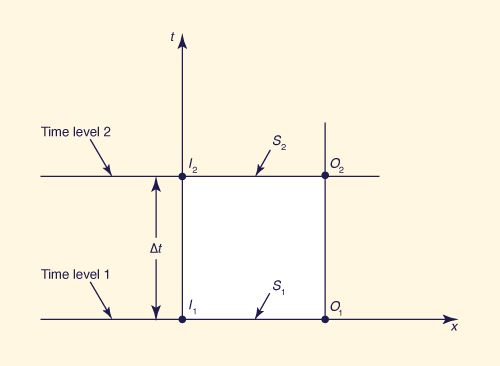
La Ecuación 2-4 puede ser solucionada de manera analítica o numérica. El enfoque numérico es usualmente preferido porque puede calcular un hidrograma de flujo de ingreso arbitrario. La solución se obtiene discretizando la Ec. 2-4 sobre el plano x-t, mostrando un gráfico de valores de una cierta variable en puntos discretos en tiempo y espacio (Fig. 2.4) La Figura 2.4 muestra dos niveles de tiempo consecutivos, 1 y 2, separados por un intervalo Δt, y dos ubicaciones espaciales que representan el flujo de ingreso y flujo de salida, con un reservorio ubicado entre ellos. La discretización de la Ec. 2-4 sobre el plano x-t es:
en la cual I1 = flujo de ingreso en el nivel del tiempo; I2 = flujo de ingreso en el nivel de tiempo 2;
Para reservorios lineales, la relación entre el almacenamiento y el flujo de salida es lineal. Por lo tanto:
y
en la cual K = constante de almacenamiento, en unidades T. Sustituyendo la Ec. 2-6 dentro de la Ec. 2-5, obtenemos para O2:
en la cual C0, C1 y C2 son coeficientes de tránsito definidos a continuación:
Como C0 + C1 + C2 = 1, los coeficientes de tránsito son interpretados como coeficientes de ponderación. Estos coeficientes de tránsito están en función de Δt /K, y el ratio del intervalo de tiempo de almacenamiento es constante. Por lo tanto, los valores de los coeficientes de tránsito son una función de Δt /K dados en la Tabla 2.1.
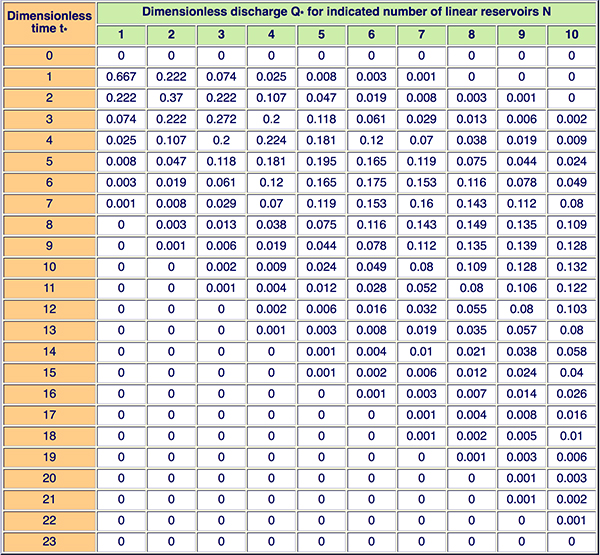
Un reservorio ejerce una acción difusiva sobre el flujo, con el resultado neto de que el pico del flujo es atenuado y, en consecuencia, incrementa el tiempo base. Para el caso de un reservorio lineal, la cantidad de atenuación está en función de Δt/K. Cuando menor es la relación, mayor es la cantidad de atenuación ejercida por el reservorio; inversamente, valores grandes de Δt/K causan menos atenuación. Nótese que los valores de Δt/K > 2 producen atenuaciones negativas (observe los valores negativos de C2 en la Col. 4, Tabla 2.1). Esto equivale a la amplificación; por lo tanto, los valores de Δt/K > 2 no son utilizados en tránsito de reservorios (Ponce, 2014a). 2.3 La cascada de reservorios lineales La cascada de reservorios lineales es un método ampliamente utilizado para tránsito hidrológico de una cuenca. Como su nombre lo indica, el método se basa en la conexión en serie de varios reservorios lineales. Para N reservorios, el flujo de salida del primero debe tomarse como el flujo de ingreso del segundo, el flujo de salida del segundo es el flujo de ingreso del tercero, y así sucesivamente, hasta que el flujo de salida del reservorio (N - 1)th, sea tomado como el flujo de ingreso del reservorio N th. El flujo de salida del reservorio N th es tomado como el flujo de salida de la cascada de reservorios lineales. Cada reservorio de la serie provée de cierta cantidad de difusión y retardo asociado. Para un grupo de parámetros Δt/K y N, el flujo de salida del último reservorio está en función del flujo de entrada del primer reservorio. De esta manera, un primer parámetro del método de reservorio lineal (Δt/K) es extendido para un segundo parámetro del método de tránsito en una cuenca. La adición del segundo parámetro (N) provee de una considerable flexibilidad en simulaciones de rango amplio de difusión y de efectos de retardo asociados. El método ha sido ampliamente utilizado en simulación de cuencas, principalmente en aplicaciones que involucran grandes cuencas hidrográficas. La información de precipitaciónescorrentía puede ser utilizada para calibrar el método, es decir, para determinar el grupo de parámetros Δt/K y N que producen el mejor ajuste a los datos medidos. La solución de la cascada de reservorios lineales puede realizarse de dos maneras: (1) analítica, y (2) numérica. La versión analítica se debe a Nash (1957), quien originó el concepto del hidrograma unitario instantáneo (HUI) (Sección 2.4). Según Nash, el hidrograma unitario instantáneo se obtiene cuando la duración tr de un hidrograma unitario se reduce indefinidamente, es decir, tr ⇒ 0. Nash asumió que el HUI puede representarse como la cascada de reservorios lineales. La versión numérica de la cascada de reservorios lineales se presenta en varios modelos de simulación hidrológica desarrollados en los Estados Unidos y otros países. Entre ellos destaca el modelo de Síntesis de Corriente y Regulación de Reservorios Stream Synthesis and Reservoir Regulation (SSARR), que se utiliza en los módulos de cuenca, tránsito de canal de corriente, y flujo base. El modelo SSARR ha estado en proceso de desarrollo y aplicación desde 1956. El modelo fue desarrollado para satisfacer las necesidades de la División del Pacífico Norte del Cuerpo de Ingenieros del Ejército de los Estados Unidos en el área de simulación matemática hidrológica para la planificación, diseño, y operación de trabajos de control del agua (U.S. Army Engineer North Pacific Division, 1972). El modelo SSARR se aplicó por primera vez para actividades de predicción de caudales de operación y gestión de ríos en el sistema del río Columbia. Posteriormente, fue utilizado por el Cuerpo de Ingenieros de los Estados Unidos, el Servicio Nacional de Meteorología, y la Administración Energética de Bonneville. Numerosos sistemas de ríos en los Estados Unidos y otros países han sido modelados con SSARR. Para derivar la ecuación de tránsito para el método de cascada de reservorios lineales, la Ec. 2-7 es reproducida en la siguiente forma diferencial:
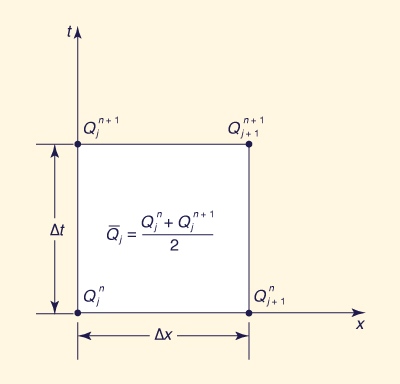
en la cual Q representa la descarga, ya sea flujo de ingreso o flujo de salida. Mientras que, j y n son indicativos de espacio y tiempo, respectivamente (Fig. 2.5).
Como en la Ec. 2-7, los coeficientes de tránsito C0, C1 y C2 son una función de la relación adimensional Δt /K. Esta relación es propiamente el número de Courant (C = Δt /K). En términos del número de Courant, las Ecs. 2-8 pueden expresarse a continuación:
Para la aplicación del tránsito de una cuenca, es conveniente definir el promedio del flujo de entrada como se muestra a continuación:
Sustituyendo las Ec. 2-10b y 2-11 dentro de la Ec. 2-9 se obtiene lo siguiente:
O, alternativamente, a través de una manipulación algebraica:
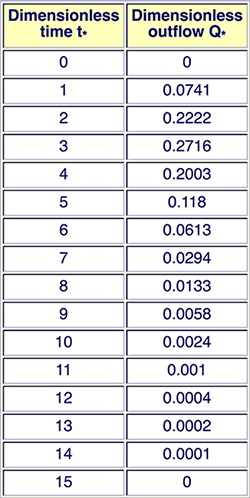
Las Ecuaciones 2-12 y 2-13 son una forma conveniente para el tránsito de cuenca porque el flujo de ingreso es usualmente un hietograma de precipitación, es decir, un valor de promedio constante por intervalo de tiempo. Notando que las Ec. 2-12 y 2-13 son idénticas. La Ec. 2-12 fue presentada por Ponce en su versión de la cascada de reservorios lineales (Ponce, 2014a). Mientras que, la Ec. 2-13 es la ecuación de tránsito del modelo SSARR (U.S. Army Engineer North Pacific Division, 1972). Valores pequeños de C conllevan a grandes cantidades de difusión de la escorrentía. Para valores de C > 2, el comportamiento de la Ec. 2-12 (o Ec. 2-13) depende en gran medida del tipo de entrada. Por ejemplo, en el caso de un impulso unitario (duración de la precipitación igual al intervalo de tiempo), la Ec. 2-12 (o Ec. 2-13) da como resultado valores negativos de flujo de salida, es decir, inestabilidad numérica. En la práctica, la Ec. 2-12 (o Ec. 2-13) están restringidos a C ≤ 2. La cascada de reservorios lineales proporciona un mecanismo conveniente para simular una amplia gama de problemas de tránsito de cuencas. Además, el método puede ser aplicado por separado para cada componente de la escorrentía (escorrentía superficial, escorrentía subsuperficial, y flujo base), y la respuesta de la cuenca puede tomarse como la suma de todas las respuestas de las componentes individuales. Por ejemplo, supongamos que una cuenca tiene 10 cm de escorrentía, de los cuales 7 cm son de escorrentía superficial, 2 cm son de escorrentía subsuperficial y 1 cm es flujo base. Dado que la escorrentía superficial es el proceso de menor difusión, puede ser simulado con un número de Courant alto, digamos C = 1, y un número pequeño de reservorios, digamos N = 3. La escorrentía subsuperficial es mucho más difusiva que la escorrentía superficial; por lo tanto, puede ser simulado con C = 0.4 y N = 5. El flujo base, que es muy difusivo, puede ser simulado con C = 0.1 y N = 7 (Ponce, 2014a). 2.4 Hidrograma unitario instantáneo Nash (1957) definió el hidrograma unitario instantáneo (HUI) como el obtenido cuando la duración tr de la precipitación efectiva disminuye indefinidamente. Además, Nash representó el HUI como una seria de n reservorios lineales, es decir, una cascada de reservorios lineales. Según Nash, la ecuación general para el hidrograma unitario instantáneo es:
en la cual u = ordenada del hidrograma unitario, y t = tiempo. En la ecuación: V = volumen del hidrograma unitario; K = constante de almacenamiento, en unidades de tiempo; n = número de reservorios en serie; y Γ(n) = función gamma. La Ecuación 2-14 es la versión analítica del HUI o de la cascada de reservorios lineales. La versión numérica es representada por el modelo de Ponce (Ec. 2-12) o del modelo SSARR (Ec. 2-13). 2.5 Hidrograma unitario instantáneo geomorfológico Rodríguez-Iturbe and Valdés (1979) son pioneros en establecer la relación del hidrograma unitario instantáneo con las características geomorfológicas de una cuenca; ver también los trabajos complementarios (Valdés et. al. 1979; Rodríguez-Iturbe et. al. 1979). Las características geomorfológicas son expresadas en términos de los siguientes parámetros de la cuenca:
Según Rodríguez-Iturbe y Valdés (1979), las ecuaciones para calcular el hidrograma unitario instantáneo geomorfológico (HUIG) son:
En la cual qp = descarga pico, en unidades T -1; 1 tp = tiempo pico, en unidades T. Los parámetros θ y k están en función de los parámetros de cuenca RA, RB, RL, y LΩ, como se muestra:
Los parámetros θ y k tiene dimensiones de L -1 y L, espectivamente. Las Ecuaciones 2-18 y 2-19 se asumen para una cuenca de orden Ω = 3, y una longitud hidráulica para una subcuenca de primer orden L1 = 1000 m. 2.6 Concepto de difusión de escorrentía El hidrograma unitario busca calcular la difusión de la escorrentía, es decir, la extensión del hidrograma en el tiempo y el espacio. En la práctica, la cantidad de difusión de escorrentía depende de si el flujo está a través de: (a) un reservorio, (b) un corriente principal, o (c) una cuenca. El flujo a través de un reservorio siempre produce difusión en la escorrentía. El flujo en una corriente principal puede o no, producir difusión en la escorrentía, dependiendo de la escala relativa de la onda del flujo, siempre que el número de Vedernikov sea menor a 1. La escala relativa de la onda del flujo está relacionada cuando la onda es: (a) cinemática, (b) difusiva, o (c) mixta cinemática-dinámica. El flujo en cuencas, produce difusión: (1) para todo los tipos de ondas, cuando el tiempo de concentración excede la duración de la precipitación efectiva, o (2) para todas las duraciones de precipitación efectiva, cuando la onda es una onda difusiva (Ponce, 2014b). 2.6.1 Difusión de la escorrentía en reservorios Los reservorios naturales o artificiales son características hidráulicas de superficies de agua que proveen difusión en la escorrentía. La difusión en la escorrentía es representada por una considerable atenuación sobre el hidrograma del flujo de ingreso, como se muestra en la Fig. 2.6.
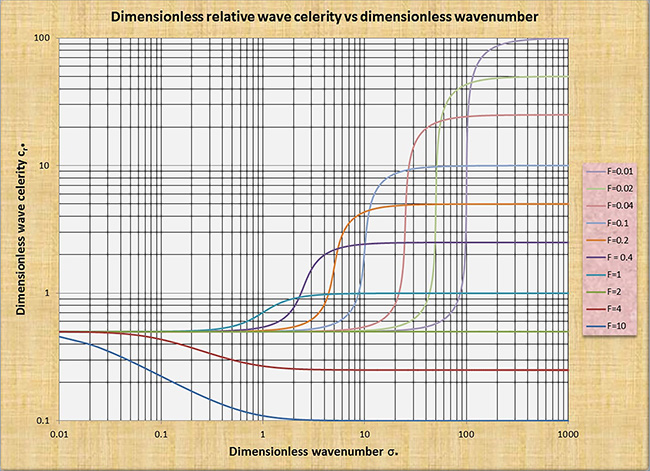
2.6.2 Difusión de la escorrentía en corrientes principales Las corrientes principales, es decir, canales, son características hidráulicas de agua superficial que puede o no, proporcionar difusión de la escorrentía, dependiendo de la escala relativa de la distorsión (onda de flujo). La cantidad de difusión de la onda se caracteriza por el número de adimensional de la onda σ, como se muestra en la Fig. 2.7. El número adimensional de la onda, se define a continuación:
en la cual L = longitud de onda distorsionada, y Lo = la longitud del canal en donde el flujo equilibrado que precipita en la cabecera es igual a su profundidad (Lighthill and Whitham, 1955):
Cuatro tipos de ondas son identificadas:
Las ondas cinemáticas tienden a encontrarse en el lado izquierdo del espectro del número de onda, caracterizado por una constante celeridad de onda relativa adimensional y de cero atenuaciones.
Para cálculos de tránsito de flujo, las ecuaciones que rigen la continuidad y movimiento, comúnmente referidas como las ecuaciones de Saint Venant, pueden ser combinadas y alineadas dentro de una ecuación de conveccióndifusión considerando la descarga Q acomo variable dependiente (Hayami, 1951; Dooge, 1973; Dooge et al., 1982; Ponce, 1991a ; Ponce, 1991b):
en la cual V = número de Vedernikov, definido como la relación entre la celeridad relativa de la onda cinemática y la celeridad relativa de la onda dinámica (Ponce, 1991b):
en la cual β = exponente de la proporción del área del flujo Q = α Aβ, Vo = velocidad media del flujo, do = profundidad media del flujo, g = aceleración de la gravedad. En la Ecuación 2-22, para V = 0, el coeficiente del término de segundo orden reduce la difusividad cinemática hidráulica, originalmente debido a Hayami (1951). Por otro lado, para V = 1, el coeficiente del término de segundo orden se reduce a cero, y el término de difusión se desvanece. Bajo esta última condición de flujo, todas las ondas, independientemente de la escala, viajan con la misma velocidad, fomentando el desarrollo de olas onduladas (Fig. 2.8).
2.6.3 Difusión de la escorrentía en cuencas La escorrentía superficial en cuencas puede ser de tres tipos (Ponce, 1989a; 2014a):
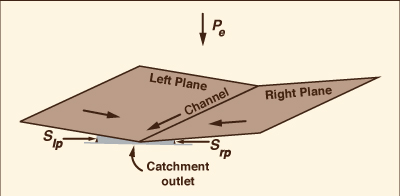
La Figura 2.9 muestra una típica esquematización de un libro abierto para modelar el flujo superficial. La entrada es la precipitación efectiva sobre dos planos adyacentes a un canal. La salida es el hidrograma de descarga de salida de la cuenca.
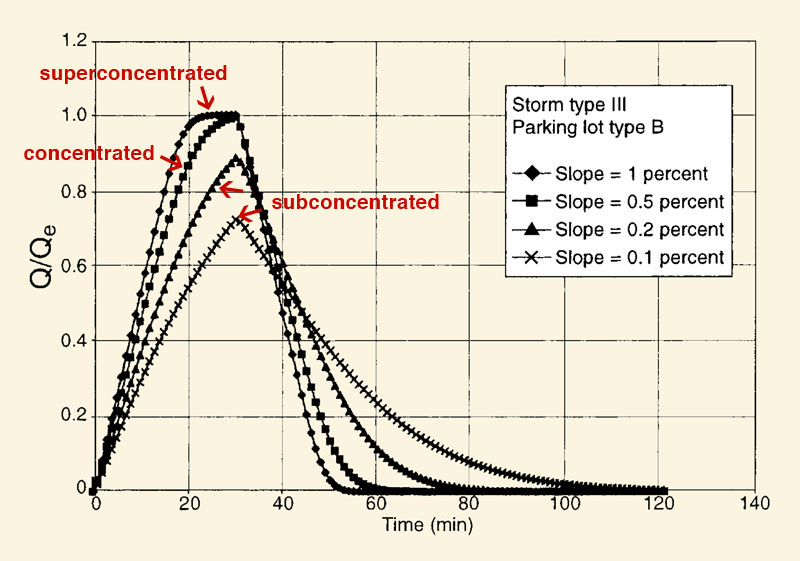
La Figura 2.10 muestra los hidrogramas adimensionales del caudal de salida de la cuenca para tres casos descritos previamente (Ponce y Klabunde, 1999). El pico máximo posible del flujo de salida es: Qp = Ie A, en dónde Ie = intensidad de precipitación efectiva, y A = área de la cuenca. Así, la difusión de la escorrentía es producida por todas las ondas cuando el tiempo de concentración excede la duración de precipitación efectiva. Esto es el caso típico para cuencas medianas y grandes, para cada cuenca la pendiente promedio de la cuenca (a lo largo de su longitud hidráulica) es suficientemente suave (pequeña). El tiempo de concentración está directamente relacionado a la longitud hidráulica de la cuenca, a la fricción de fondo, e inversamente relacionado con la pendiente de fondo y la intensidad de precipitación efectiva (Ponce, 1989b; 2014b).
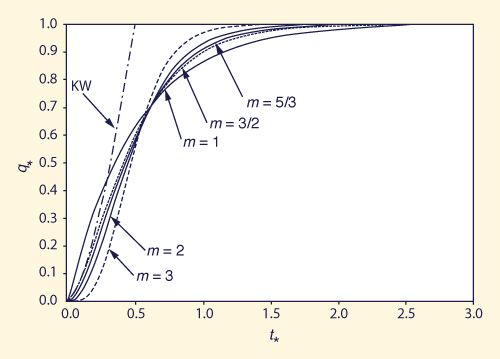
La Figura 2.11, muestra el ascenso de los hidrogramas adimensionales del flujo superficial para un modelo de onda cinemática (denominado KW) y para varios modelos conceptuales de almacenamiento, considerando que el intervalo del exponente de área-descarga m va desde m = 1, que corresponde a un reservorio lineal, para m = 3, corresponde un flujo laminar (Ponce et al., 1997). El tiempo de equilibrio de la onda cinemática, puede ser similar al tiempo de concentración, esto teóricamente es igual a la mitad del tiempo de concentración de los modelos de almacenamiento-base (Ponce, 1989; 2014). Se observó que los modelos de almacenamiento atenúan el hidrograma y, en consecuencia, producen difusión, mientras que el modelo de onda cinemática carece completamente de la difusión de la escorrentía. El tiempo de equilibrio cinemático es el valor más corto posible del tiempo de concentración, resultando, en la agrupación, en los picos de flujo más grandes. Además, bajo un flujo cinemático puro, la difusión de la escorrentía se desvanece.
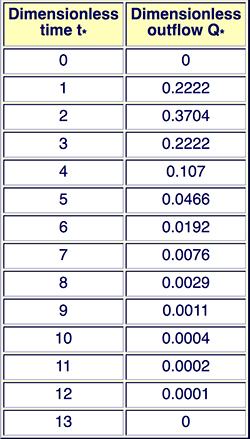
En los cálculos numéricos actuales, un modelo de onda cinemática no puede estar totalmente provisto de difusión, debido a la aparición de la difusión numérica (Cunge, 1969; Ponce, 1991a). 2.7 Hidrograma unitario adimensional general La cascada de reservorios lineales CLR (Sección 2.3) y el hidrograma unitario instantáneo (HUI) (Sección 2.4) son esencialmente lo mismo. Un hidrograma unitario adimensional general (HUAG) puede ser generado utilizando el método de la CRL para una cuenca de área de drenaje A y una duración de hidrograma unitario tr. El hidrograma unitario adimensional resultante muestra que es únicamente una función del número de Courant C y del número de reservorios N, por lo tanto, es independiente del A o tr. Además, para un conjunto de C y N, existe un único HUAG, de aplicabilidad global (Ponce, 2009). El tiempo adimensional t* está definido a continuación:
en la cual t = tiempo, y tr = tiempo de duración del hidrograma unitario.
La descarga adimensional Q* está definido a continuación:
en la cual Q = descarga, y Qmax = descarga máxima, es decir, la obtenida en ausencia de la difusión de la escorrentía (Ponce, 2014):
en la cual: i = intensidad de precipitación efectiva, en unidades L T -1; y A = área de drenaje de la cuenca, en unidades L2. Por lo tanto:
En unidades del SI, para la unidad de profundidad de precipitación de 1 cm:
Entonces:
en la cual Q es en unidades m3/s, tr está en hr y A en km2.
En la práctica, un grupo de C y N son seleccionados de tal manera que las propiedades de difusión de la escorrentía de una cuenca sean representadas en un HUAG. Las cuencas empinadas requieren de un C alto y de un N pequeño; por lo contrario, las cuencas suaves requieren de un C pequeño y de un N alto. El rango práctico de los parámetros es: 0.1 ≤ C ≤ 2; y Una vez seleccionado el HUAG, las ordenadas del hidrograma unitario pueden ser calculadas de la Ec. 2-29 como se muestra:
Del mismo modo, la abscisa (tiempo) puede ser calculada de la Ec. 2-24 como se muestra:
El hidrograma unitario calculado se puede convolucionar con el hietograma de precipitación efectiva para determinar el hidrograma de flujo compuesto (Ponce, 2014). El HUAG tiene las siguientes ventajas significativas:
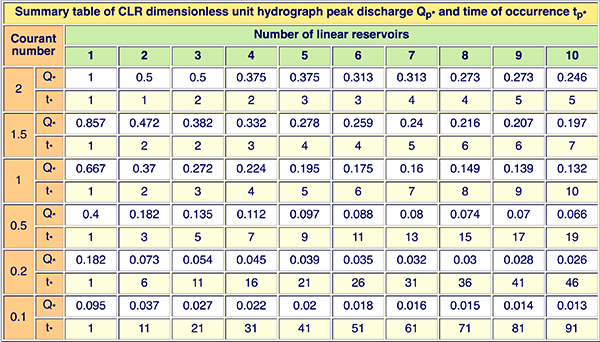
Los parámetros de la cascada del HUAG (C y N) son estimados en base a las propiedades de difusión de la escorrentía de la cuenca en consideración. Las propiedades de difusión de la escorrentía dependen en gran medida de la topografía y geomorfología del terreno en general. En la naturaleza, las cuencas se clasifican de acuerdo a la difusión de la escorrentía basada en su pendiente promedio superficial de terreno. Una clasificación preliminar se muestra en la Tabla 2.2 (Ponce, 2009). Esta tabla muestra la variedad de clases geomorfológicas y su rango asociado de pendiente promedio superficial terrestre, con los parámetros de cascada estimados y los valores pico correspondientes al HUAG Q*p and time t*p). La tabla 2.2 puede utilizarse como referencia para la evaluación preliminar de C y N para una cuenca específica.
3. METODOLOGÍA
3.1 Visión La metodología para el estudio tiene el objetivo de desarrollar una relación entre los parámetros de cascada del HUAG (C y N) y las respectivas características geomorfológicas de la cuenca. Para este propósito, son seleccionadas adecuadamente varias cuencas en California, que reúnen una amplia gama de características geomorfológicas, en particular la pendiente promedio de la superficie del terreno y la pendiente del canal principal. Para los datos diarios, el intervalo de tiempo de análisis es de 1 día (tr = 1 día). La metodología seleccionada depende de las características temporales de la tormenta. Las siguientes dos situaciones son consideradas:
3.1.1 Tormentas simples Para las tormentas simples, los siguientes pasos son requeridos:
3.1.2 Tormentas complejas Para las tormentas complejas, los siguientes pasos son requeridos:
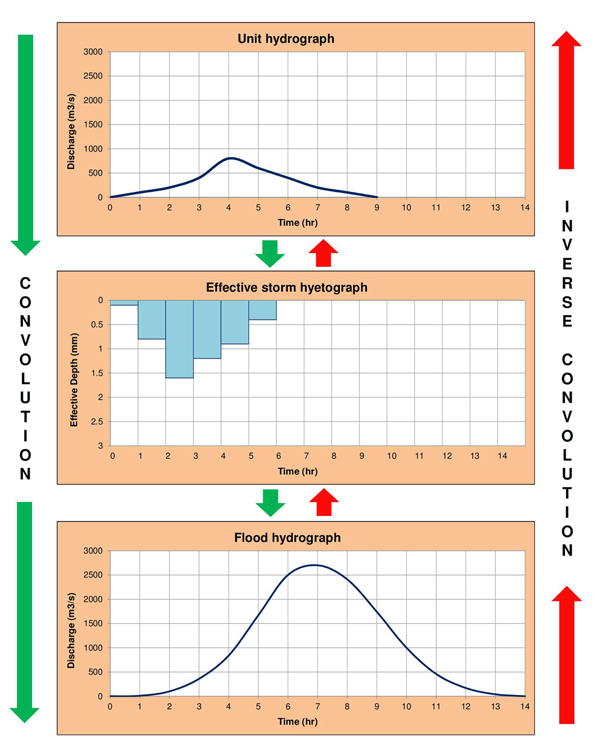
Para cada cuenca analizada, un grupo de pares referente a los parámetros de cascada C y N son relacionados con las características geomorfológicas primarias de la cuenca, como la pendiente del canal principal / superficial. En una aplicación práctica, una vez que se determina la pendiente promedio del canal principal y la pendiente promedio de la superficie del terreno, los valores apropiados de C y N son utilizados para calcular el hidrograma unitario adimensional (HUA). Este último es utilizado, junto con el área de la cuenca A y la duración del hidrograma unitario tr (Ec. 2-30 y 2-31, respectivamente), para calcular el hidrograma unitario (HU). 3.2 Convolución y convolución inversa La convolución es el procedimiento por el cual un cierto hidrograma unitario y un hietograma de precipitación efectiva son utilizados para calcular el hidrograma de inundación. Por el contrario, la convolución inversa es el procedimiento por el cual cierto hidrograma de inundación y una hietograma de precipitación efectiva son utilizados para calcular el hidrograma unitario correspondiente.
Fig. 3.1 Convolución y convolución inversa.
El procedimiento de la convolución está basado en los principios de linealidad y superposición.
El procedimiento de la convolución se ilustra mediante el siguiente ejemplo. Suponga que se ha derivado el siguiente hidrograma unitario de 1 h para una cuenca determinada:
Una tormenta de 6 horas con una precipitación efectiva total de 5 cm que cubre toda una cuenca, tiene una distribución de tiempo como se muestra:
El hidrograma compuesto (inundación) se calcula usando la técnica de convolución, como se muestra (Tabla 3.3):
La suma de la Col. 2 es de 2800 m3/s y equivale a 1 cm de precipitación neta. Se verifica la suma de la Col. 9 que es 14000 m3/s, y, por lo tanto, el equivalente de 5 cm de precipitación efectiva. 3.2.2 Convolución inversa El procedimiento de la convolución inversa permite el cálculo de un hidrograma unitario basado en un hietograma de precipitación efectiva y un hidrograma compuesto (inundación). El procedimiento se denomina método de sustitución directa (Ponce, 2014). El hidrograma unitario puede ser calculado directamente debido a la propiedad con bandas de la matriz de convolución (ver Tabla 3.3). Con m = número de ordenadas no nulas del hidrograma unitario, n = número de intervalos de precipitaciones efectivas, y N = número de ordenadas no nulas del hidrograma de la tormenta, la relación a cumplir es la siguiente:
Por lo tanto:
Por eliminación y sustitución posterior, se desarrolló la siguiente fórmula para las ordenadas del hidrograma unitario ui como una función de las ordenadas del hidrograma de la tormenta qi, y de la profundidad de precipitación efectiva rk, para i que varía de 1 a m:
En la sumatoria del término de la Ec. 3-4, j decrece de j -1 a 1, y k incrementa de 2 hasta un máximo de n. Esta Ecuación 3-3 (recursiva) permite el cálculo directo de un hidrograma unitario basado en un hidrograma de tormenta compleja. En la práctica, sin embargo, no siempre es posible llegar a una solución, ya que puede ser difícil obtener una combinación perfecta entre un hidrograma compuesto (inundación) y un hietograma de precipitación efectiva (debido al ruido de los datos). Nótese que el hidrograma de tormenta (medido) tendría que estar separado de la escorrentía directa y flujo base antes de intentar utilizar la Ec. 3-3. El procedimiento de la convolución inversa está ilustrado por su aplicación en la Ec. 3-4 en el ejemplo de la Tabla 3.3. Usando la Ec. 3-2, con el número no nulo de las ordenadas del hietograma de tormenta N = 13, y el número de intervalos de la precipitación efectiva n = 6, el número de ordenadas no nulas del hidrograma unitario es: m = 8. Por lo tanto:
El resultado confirma las ordenadas del hidrograma unitario mostrado en la Col. 2 de la Tabla 3.3. 3.3 Hidrograma unitario adimensional general
La teoría del hidrograma unitario adimensional general (HUAG) fue desarrollado por Ponce
Ponce (2009).
Un HUAG puede ser generado utilizando (Sección 2.3) el método de cascada de reservorios lineales (CRL) para una cuenca de área de drenaje A y una duración de hidrograma unitario tr.
Una versión Web (en línea) del HUAG como una función de C y N está determinado en el enlace ponce.sdsu.edu/online_general_uh_cascade.
La Figura 3.2 muestra un ejemplo de salida para C = 1 y N = 3. El programa es utilizado en la Sección 5.1 para ajustar los hidrogramas unitarios adimensionales: medido y Predicho.
Fig. 3.2 Hidrograma unitario adimensional para C = 1 y N = 3.
Una versión Web (en línea) del HUAG para series de C (se recomienda un rango 0.1 ≤ C ≤ 2.0) y para todos los valores de N en el rango 1 ≤ N ≤ 10 están dados en el enlace ponce.sdsu.edu/online_series_uh_cascade. La Fig. 3.3 muestra un ejemplo de salida para C = 1. Comparamos los valores de las descargas de la Fig. 3.3 para N = 3 con los valores de la Fig. 3.2.
Fig. 3.3 Hidrograma unitario adimensional para C = 1 y 1 ≤ N ≤ 10.
Una versión Web (en línea) de las series del HUAG para seis (6) valores de C que se encuentren en el rango recomendado (2.0, 1.5, 1.0, 0.5, 0.2, y 0.1), y para todos los valores de N del rango recomendado de 1 ≤ N ≤ 10, se encuentra en el enlace ponce.sdsu.eduonline_all_series_uh_cascade. La Fig. 3.2 muestra un
resumen de la descarga pico adimensional Qp* del tiempo de ocurrencia tp*. Comparar el resultado para el número de Courant de C = 1 y N = 3 en la Fig. 3.4 con el resultado de la Fig. 3.3 (t* = 3; Q* = 0.272).
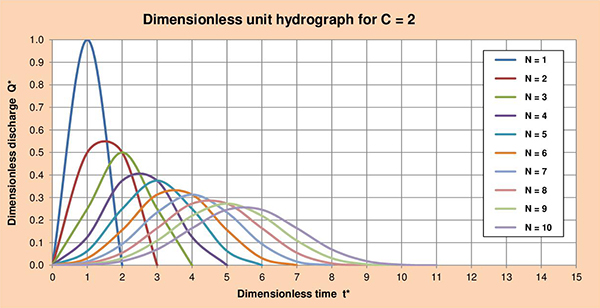
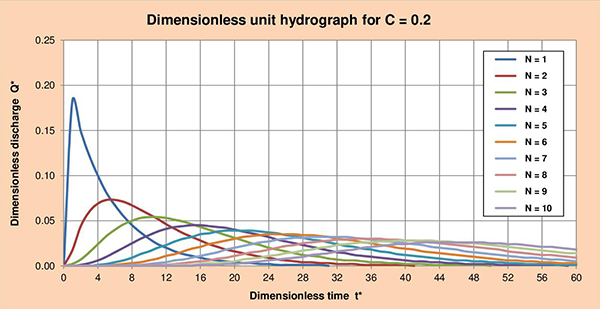
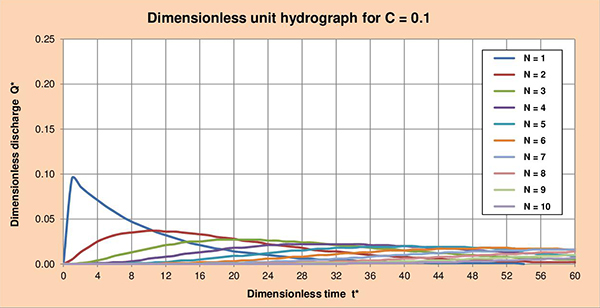
Fig. 3.4 Hidrograma unitario adimensional para 2 < C ≤ 0.1, and 1 ≤ N ≤ 10. 3.4 Series de los hidrogramas unitarios Las Figuras 3.5 (a) hasta la (f), muestran las series de los hidrogramas unitarios adimensionales (HUA) para los parámetros de cascada C con valores de 2, 1.5, 1, 0.5, 0.2 y 0.1; y valores de N que varían entre 1 y 10. La examinación de estas figuras nos permite identificar las siguientes conclusiones:
Fig. 3.5 (a) Hidrograma unitario adimensional para C = 2.
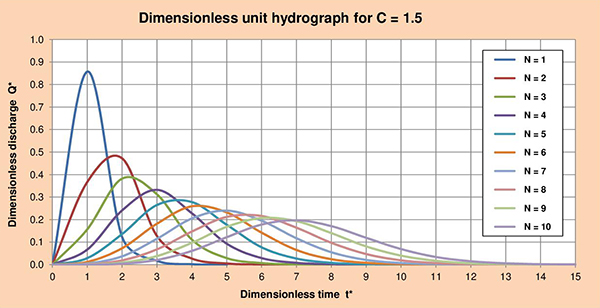
Fig. 3.5 (b) Hidrograma unitario adimensional para C = 1.5.
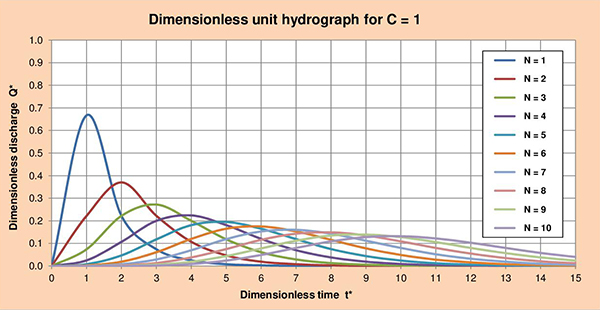
Fig. 3.5 (c) Hidrograma unitario adimensional para C = 1.
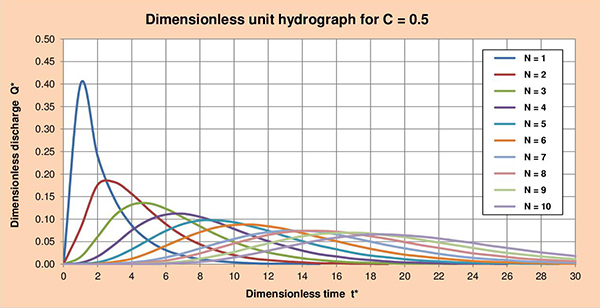
Fig. 3.5 (d) Hidrograma unitario adimensional para C = 0.5.
Fig. 3.5 (e) Hidrograma unitario adimensional para C = 0.2.
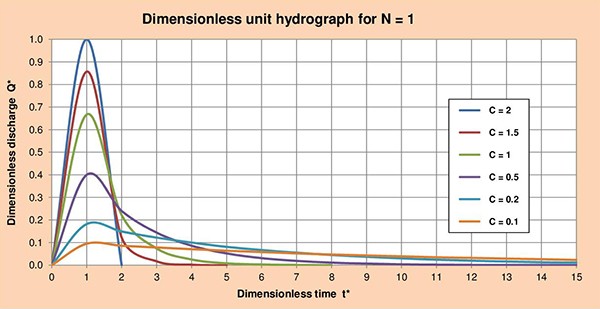
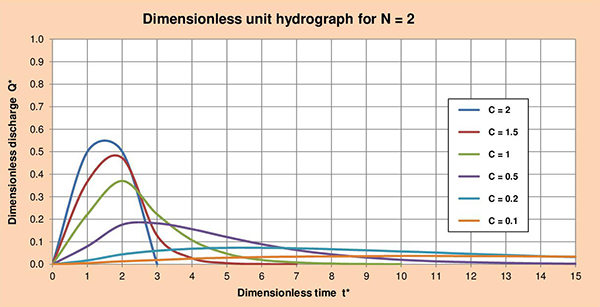
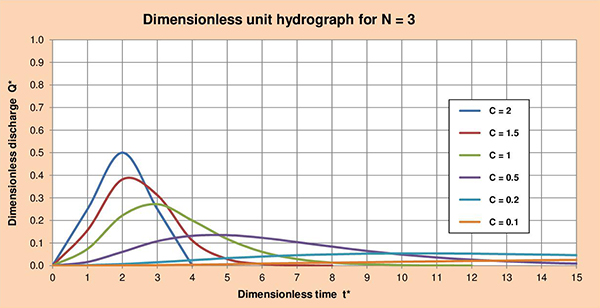
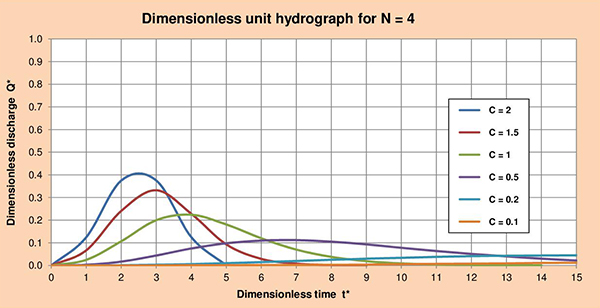
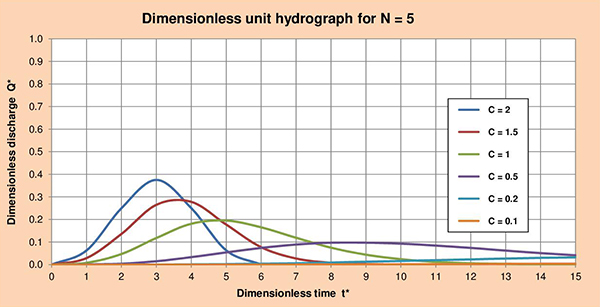
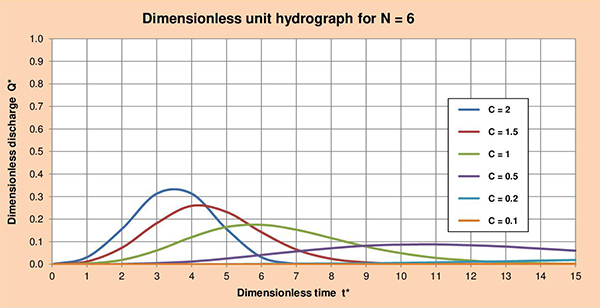
Fig. 3.5 (f) Hidrograma unitario adimensional para C = 0.1. Las Figuras 3.6 (a) hasta (f), muestran las series de hidrogramas unitarios adimensionales (HUA) para los parámetros de cascada N con valores de 1, 2, 3, 4, 5 y 6; y valores de C que varían entre 2 y 0.1. La examinación de estas figuras nos permite identificar las siguientes conclusiones:
Fig. 3.6 (a) Hidrograma unitario adimensional para N = 1.
Fig. 3.6 (b) Hidrograma unitario adimensional para N = 2.
Fig. 3.6 (c) Hidrograma unitario adimensional para N = 3.
Fig. 3.6 (d) Hidrograma unitario adimensional para N = 4.
Fig. 3.6 (e) Hidrograma unitario adimensional para N = 5.
Fig. 3.6 (f) Hidrograma unitario adimensional para N = 6. 3.5 HUAG, CRL y convolución
La cascada de reservorios lineales (CRL) de la Sección 2.3 y la convolución del hidrograma unitario con el hietograma de precipitación efectiva (Sección 3.2.1) conducen al mismo hidrograma compuesto de inundación, provisto de los parámetros de cascada (HUAG) que son utilizados para desarrollar el hidrograma unitario para la convolución. Estas proposiciones son sustentadas con el siguiente ejemplo:
Asumiendo un hietograma de precipitación efectiva de 6 horas mostrado en la Tabla 3.2.
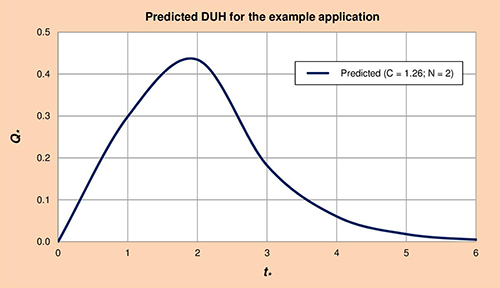
Asumiendo un área de drenaje: A = 432 km2. La duración del hidrograma unitario aplicable tr es la misma que del intervalo de tiempo del hietograma de precipitación efectiva (Tabla 3.2), i.e., tr = Δt = 1 hr. Supongamos que la cuenca tiene un relieve reltivamente empinado, con parámetros de cascada C = 1 y N = 2. Una versión Web (en línea) del HUAG en función de C and N se muestra en el enlace ponce.sdsu.edu/online_general_uh_cascade. El HUA correspondiente se muestra en la Fig. 3.7.
Fig. 3.7 Hidrograma unitario adimensional para C = 1 y N = 2. Dada la constante de almacenamiento del reservorio K:
El tiempo
Y la de descarga:
El calculador en línea ponce.sdsu.edu/online_dimensionless_uh_cascade muestra el hidrograma unitario y el hidrograma unitario adimensional, mostrados en la Fig. 3.8.
Fig. 3.8 Hidrograma unitario e hidrograma unitario adimensional para C = 1 and N = 2.
Con C = 1 (i.e., K = 1), N = 2, y el hietograma de precipitación efectiva de la (Table 3.2), el calculador Web (en línea) ponce.sdsu.edu/online_routing_08
calcula el hidrograma compuesto de inundación por la cascada de reservorios lineales (Ponce 1989).
El hidrograma compuesto de inundación se muestra en la Fig. 3.9.
Fig. 3.9 Hidrograma compuesto de inundación por la cascada de reservorios lineales (CRL).
La convolución del hidrograma unitario (Fig. 3.8, Cols. 2 y 3) con el hietograma de precipitación efectiva (Tabla 3.2) se complementan para utilizar el calculador Web (en línea) del enlace ponce.sdsu.edu/online_convolution. Para este ejemplo, es aplicable el hietograma de precipitación efectiva; por lo tanto, el número de curva es: CN = 100. El hidrograma compuesto de inundación se muestra en la Fig. 3.10. Sorprendentemente, se confirma que los resultados de las Figs. 3.9 y 3.10 son esencialmente los mismos.
Fig. 3.10 Hidrograma compuesto de inundación por convolución.
En resumen, dado un grupo de parámetros de cascada C y N, y un hietograma de precipitación efectiva, el método de cascada de reservorios lineales (CRL) puede utilizarse para calcular el hidrograma compuesto de inundación. Asimismo, la convolución de un hidrograma unitario derivado con el método del HUAG, y utilizando el mismo grupo de parámetros de cascada (C y N), puede utilizarse para calcular el hidrograma compuesto de inundación. Se demuestra que estos dos
hidrogramas de inundación son los mismos.
4. ANÁLISIS DE DATOS
4.1 Antecedentes Se seleccionaron varias cuencas en California, con un rango amplio de características geomorfológicas. Los requerimientos para encontrar las cuencas fueron las siguientes:
4.2 Fuente de información La información geomorfológica e hidrometeorológica se recolectó de los siguientes medios:
4.3 Parámetros geomorfológicos 4.3.1 Área de drenaje El área de drenaje determina el volumen potencial de la escorrentía, provisto por una tormenta que cubre toda la superficie. La división de una cuenca está en los puntos que delimitan dos cuencas adyacentes, es decir, la recolección de puntos altos (picos y depresiones) que separan las cuencas que drenan en diferentes direcciones (salidas). En esta investigación, las áreas de las cuencas se obtuvieron con la ayuda de Sistemas de Información Geográfica (SIG). 4.3.2 Perímetro de drenaje El perímetro del área de drenaje es la suma de la longitud que delimita la cuenca. Los perímetros de las cuencas se obtuvieron con la ayuda de Sistemas de Información Geográfica (SIG). 4.3.3 Longitud hidráulica de la cuenca
La longitud hidráulica es la longitud medida a lo largo del curso de agua principal de la cuenca. 4.3.4 Índice de forma El índice de forma de una cuenca está definido con la siguiente ecuación:
en la cual Kf = índice de forma, A = área de drenaje en unidades, y L = longitud de la cuenca, medida del curso de agua más largo. El área y la longitud se dan en unidades consistentes, como km2 cuadrados y km, respectivamente. 4.3.5 Índice de compacidad Es una alternativa de descripción morfológica que se basa en el perímetro de la cuenca más que en el área. Para este propósito, un círculo equivalente es definido como un círculo de área igual al de la cuenca. El índice de compacidad es la relación entre el perímetro de la cuenca y su círculo equivalente. Esto se puede expresar a continuación:
en la cual Kc = índice de compacidad, P = perímetro de la cuenca, y A = área de la cuenca. 4.3.6 Elevación máxima y mínima La elevación máxima es el punto más alto donde se divide la cuenca, mientras que la elevación mínima es el punto de salida de la cuenca. La diferencia entre estos dos puntos de referencia es relieve de la cuenca. Las elevaciones se obtuvieron con la ayuda de Sistemas de Información Geográfica (SIG). 4.3.7 Pendiente promedio de la superficie del terreno Los métodos de malla (grilla) se utilizan a menudo para obtener medidas de la pendiente de la superficie del terreno para las evaluaciones de escorrentía. Por ejemplo, el Servicio de Conservación de Recursos Naturales (NRCS) del USDA determina la pendiente promedio de la superficie al superponer un patrón de malla sobre el mapa topográfico de la cuenca. Se evalúa la pendiente máxima de la superficie en cada intersección de la malla y se calcula el promedio de todos los valores. Este promedio se toma como el valor representativo de la pendiente de la superficie del terreno. El procedimiento se realizó con la ayuda de GIS, y la pendiente promedio de la superficie del terreno se denominó S0. 4.3.8 Pendiente promedio del canal principal El gradiente del canal de curso de agua principal es un indicador conveniente del relieve de una cuenca. Un perfil longitudinal es definido por sus elevaciones máximas (aguas arriba) y mínimas (aguas abajo), y por la distancia horizontal entre ellas. El gradiente del curso de agua obtenido directamente desde las elevaciones aguas arriba y aguas abajo se denomina pendiente S1. Una alternativa para obtener la pendiente del canal principal es calcular la pendiente entre dos puntos del perfil longitudinal, situados al 10% y 85% del punto de vertido o salida, respectivamente. Este procedimiento es recomendado por el United States Geological Service USGS (Ponce, 2014a). Está pendiente del canal principal se denominó como S2. 4.3.9 Longitud total del canal principal La longitud total del canal principal es la suma de todos los canales naturales definidos en el interior de la cuenca. Este procedimiento se realizó con ayuda de Sistemas de Información Geográfica (SIG). 4.3.10 Densidad de drenaje La densidad de drenaje de la cuenca es la relación entre la longitud total de la corriente y el área de la cuenca. Una densidad de drenaje alta refleja una respuesta de escorrentía rápida y máxima, mientras que una densidad de drenaje baja es característica de una respuesta de escorrentía retardada. 4.3.11 Precipitación media anual Las precipitaciones varían no solo en el tiempo sino también en el espacio, es decir, la misma cantidad de lluvia no cae uniformemente en toda la cuenca. Las isoyetas se utilizan para representar la variación espacial de las precipitaciones. Una isoyeta es una línea de contorno que muestra los lugares de igual profundidad de lluvia. El análisis de isoyetas se realizó con la ayuda de SIG. 4.4 Selección de cuencas Se seleccionaron diez (10) cuencas ubicadas en California para el análisis de la investigación. Las cuencas se enumeran en la 4.1.
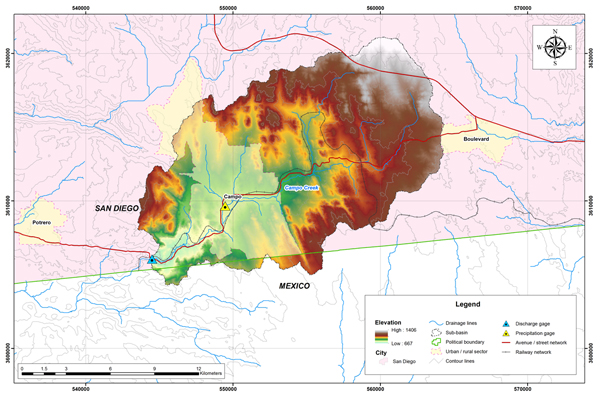
4.4.1 Quebrada Campo en Campo, CA
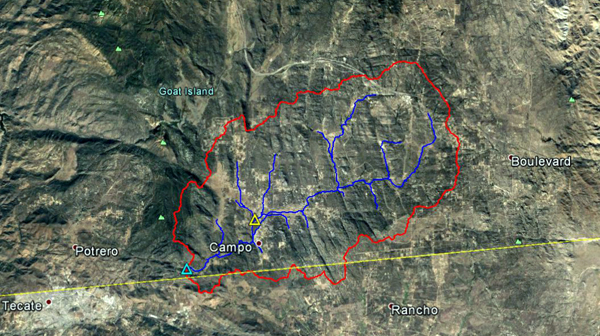
La cabecera de la subcuenca de la quebrada Campo está localizada cerca de la comunidad de Live Oak Springs, en el sureste del condado de San Diego, California (Fotografía 4.1). La corriente fluye en dirección predominante suroeste cruzando la comunidad de Campo (Fotografía 4.2.). La estación meteorológica del National Weather Service (NWS) se localiza en Campo (Fotografía 4.3).
Fig. 4.1 Vista aguas abajo de la quebrada Campo cerca de la cabecera de la subcuenca.
Fig. 4.2 Vista aguas arriba de la quebrada Campo, California.
Fig. 4.3 Estación de precipitación del NOAA NWS en Campo, California.
Fig. 4.4 Estación de hidrométrica del USGS en la intersección de la quebrada Campo con la ruta estatal Nro. 94.
Después de cruzar a México, la quebrada de Campo se renombra como Cañada Joe Bill, que desemboca en la quebrada Tecate en la localidad de Tecate. A su vez, la quebrada Tecate desemboca en el río Tijuana, este último finalmente desemboca en el Océano Pacífico en Imperial Beach, California.
Fig. 4.5 Vista aérea de la subcuenca de la quebrada Campo.
Fig. 4.6 Mapa hidrológico de la subcuenca de la quebrada Campo.
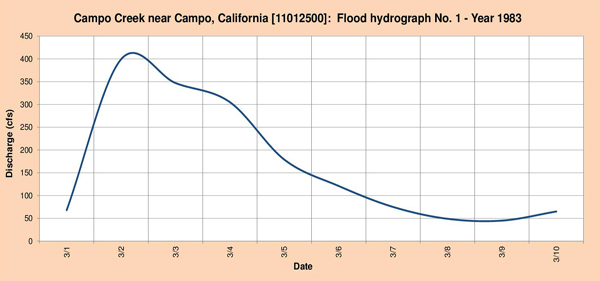
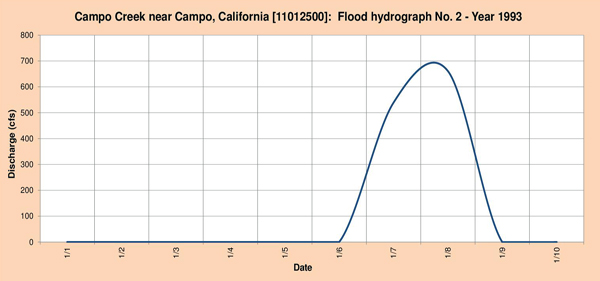
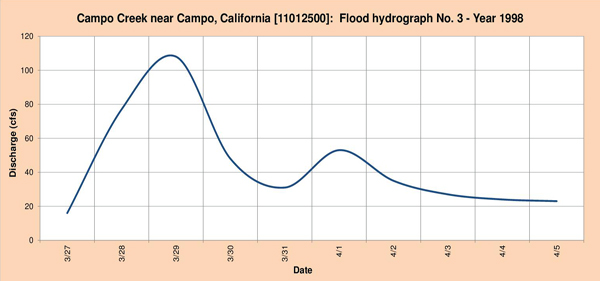
La Figura 4.7 muestra los tres (3) hidrogramas de crecidas seleccionados para el análisis.
Fig. 4.7 (a) Hidrograma de inundación de la quebrada Campo Nro. 1 - Año 1983.
Fig. 4.7 (b) Hidrograma de inundación de la quebrada Campo Nro. 2 - Año 1993.
Fig. 4.7 (c) Hidrograma de inundación de la quebrada Campo No. 3 - Año 1998.
La cabera de la cuenca del río Whitewater está localizada cerca de la montaña San Gorgonio, al sureste de la ciudad de Forest Falls, California. La corriente (Fotografía 4.5), hasta drenar en el mar Saltón (Fotografía 4.6). Las estaciones meteorológicas del National Weather Service (NWS) están localizadas en las ciudades de Palm Springs, Indio y Palm Desert. La estación hidrométrica del United States Geological Service (USGS) está localizada cerca de la entrada del mar Saltón.
Fig. 4.8 Vista del Cañón del río Whitewater.
Fig. 4.9 Ingreso del río Whitewater al mar Saltón.
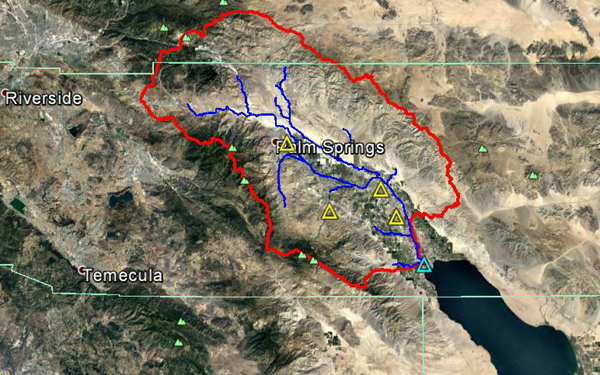
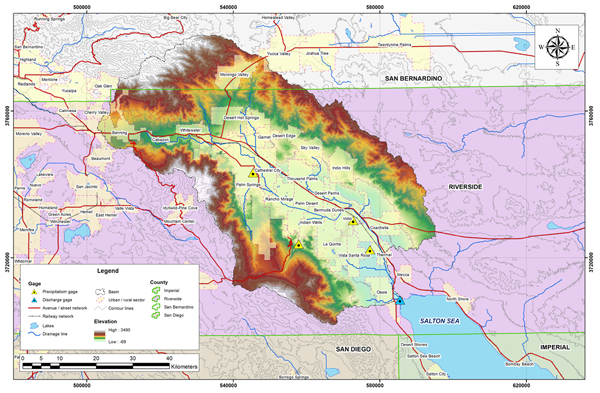
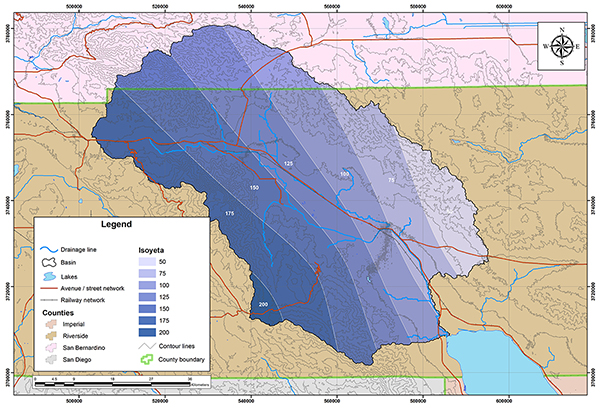
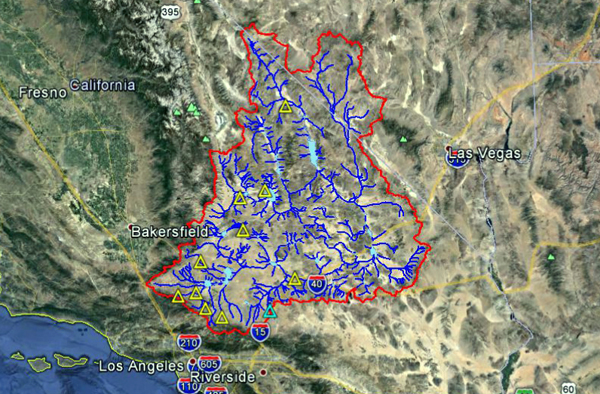
La Figura 4.4 muestra la delimitación de la cuenca del río Whitewater. La mayor parte de la cuenca está localizada en el condado de Riverside. Sin embargo, una pequeña fracción está localizada en el condado de San Bernardino. Esta agrícola desarrollada al sureste de California, cuenta con un clima de verano frío/caliente según la clasificación climática de Koppen. La precipitación media anual es 112 mm (4.41''). Las Figuras 4.5 y 4.6 muestran el mapa hidrológico y el mapa de precipitación media anual de la cuenca del río Whitewater.
Fig. 4.10 Vista aérea de la cuenca del río Whitewater.
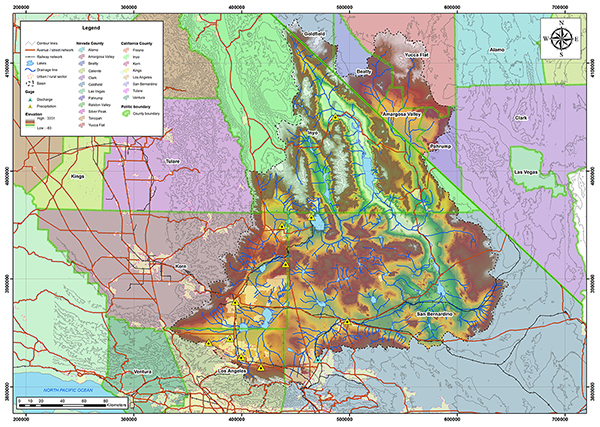
Fig. 4.11 Mapa hidrológico de la cuenca del río Whitewater.
Fig. 4.12 Mapa de precipitación media anual de la cuenca del río Whitewater. La Tabla 4.4 muestra la relación de estaciones de datos de precipitación y descargas para la cuenca del río Whitewater. La Tabla 4.5 muestra los parámetros geomorfológicos e hidrológicos calculados para la cuenca del río Whitewater.
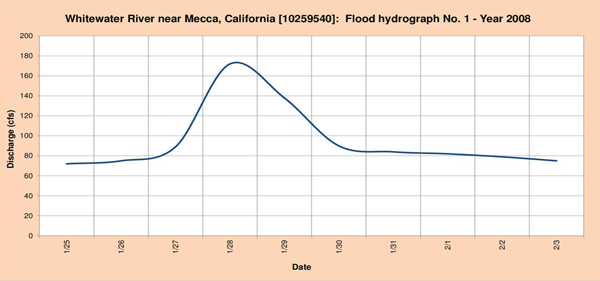
Las Figuras 4.7(a) a 4.7(c), muestran los tres (3) hidrogramas de inundación seleccionados para el análisis.
Fig. 4.13 (a) Hidrograma de inundación del río Whitewater Nro. 1-Año 2008.
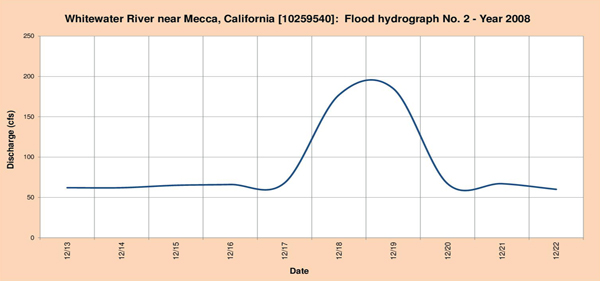
Fig. 4.13 (b) Hidrograma de inundación del río Whitewater Nro. 2-Año 2008.
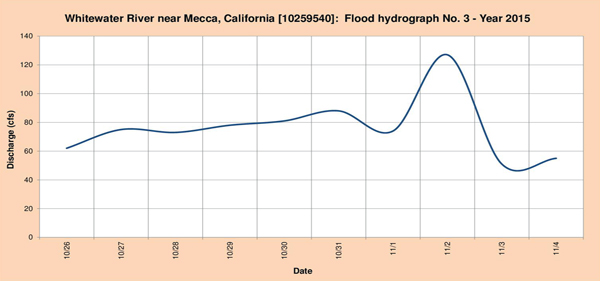
Fig. 4.13 (c) Hidrograma de inundación del río Whitewater Nro. 3-Año 2015.
La cabecera de la cuenca del río Mojave está localizada en las cercanías de las zonas montañosas de Indian Wells, Cantil, Peasonville, Darwin, Cañon Afton (Fotografía 4.7), Montaña Blanco, Montaña Sylvana, Montaña Gold, Montaña Palmer, Beatty, Valle Amargosa, Montaña Clark y Baker.
Fig. 4.14 Cruce del río Mojave en la zona del Cañón Afton, California.
Fig. 4.15 Río Mojave en la zona de Helendale, California.
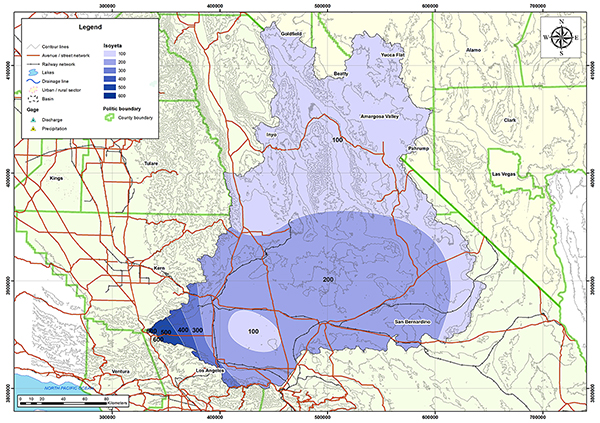
La Figura 4.16 muestra la delimitación de la cuenca del río Mojave. La cuenca está localizada en los condados de Kern, Los ángeles, Inyo y San Bernardino en California; y en los condados de Goldfiel, Beatty, Yucca Flat, Valle Amargosa y Pahrump en Nevada. Según la clasificación climática de Koppen su clima es desértico (BWk). La precipitación media anual es de 109 mm (4.29").
Fig. 4.16 Vista aérea de la cuenca del río Mojave.
Fig. 4.17 Mapa hidrológico de la cuenca del río Mojave.
Fig. 4.18 Mapa de precipitación media anual de la cuenca del río Mojave. La Tabla 4.6 muestra la relación de estaciones de datos de precipitación y descargas para la cuenca del río Mojave. La Tabla 4.7 muestra los parámetros geomorfológicos e hidrológicos calculados para la cuenca del río Mojave.
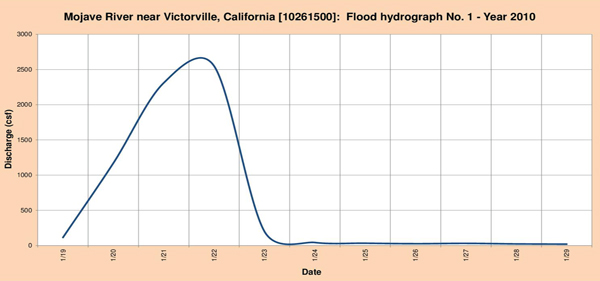
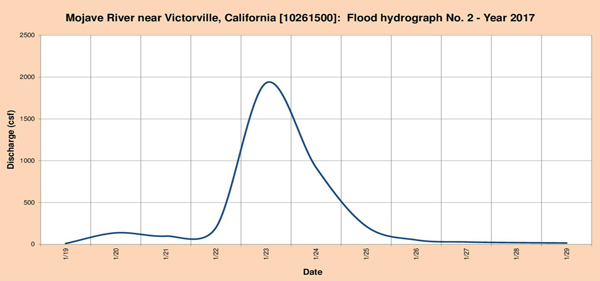
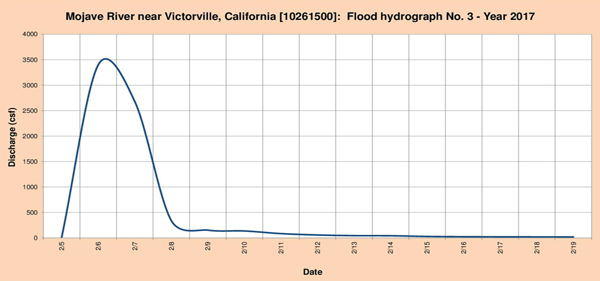
Las Figuras 4.11 de (a) hasta (c), muestran los tres (3) hidrogramas de inundación seleccionados para el análisis.
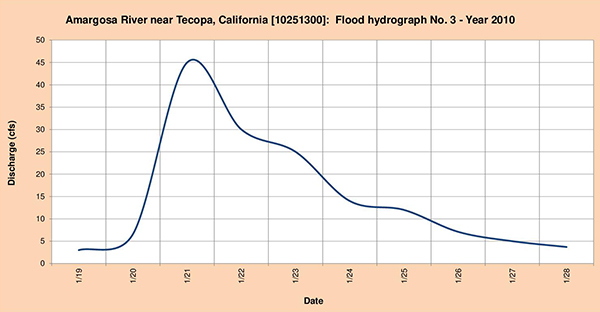
Fig. 4.19 (a) Hidrograma de inundación del río Mojave Nro. 1-Año 2010.
Fig. 4.19 (b) Hidrograma de inundación del río Mojave Nro. 2-Año 2017
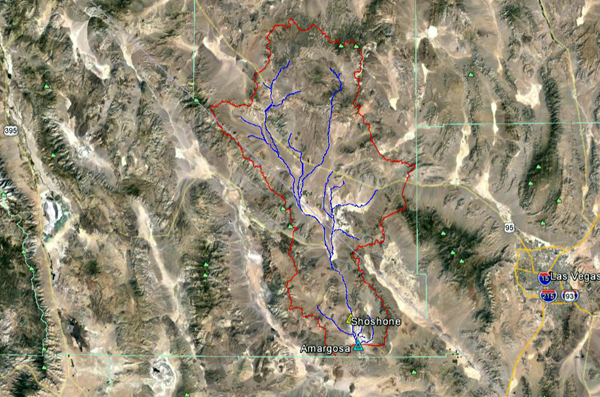
Fig. 4.19 (c) Hidrograma de inundación del río Mojave Nro. 3-Año 2017. La cabecera de cuenca del río Amargosa está localizada en las cercanías de la Montaña Timber, Montaña Negra, la comunidad de Beatty, Shoshone y Valle Amargosa (Fotografía 4.20). La corriente fluye predominantemente en dirección sureste cruzando las comunidades de Beatty, Valle Amargosa, Evelyn, Shoshone y Tecopa (Fotografía 4.21). La estación meteorológica del National Weather Service (NWS) está localizada en Shoshone. La estación hidrométrica del United States Geological Service (USGS) está localizada cerca en Tecopa.
Fig. 4.20 Aguas arriba del río Amargosa, California
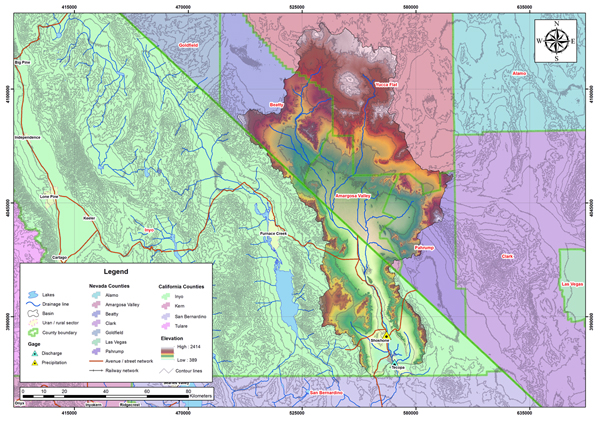
Fig. 4.21 Río Amargosa en Shoshone, California. La Figura 4.22 muestra la delimitación de la cuenca del río Amargosa. La cuenca está ubicada en el condado de Inyo de California; y los condados de Nevada de Beatty, Yucca Flat, Amargosa Valley y Pahrump. El clima corresponde al clima frío del desierto de Koppen (BWk). La precipitación media anual es de 110 mm (4.32 pulgadas). Las Figuras 4.23 y 4.24 muestran el mapa hidrológico y el mapa de precipitación media anual de la cuenca del río Amargosa.
Fig. 4.22 Vista aérea de la cuenca del río Amargosa.
Fig. 4.23 Mapa hidrológico de la cuenca del río Amargosa. La Tabla 4.8 muestra la relación de estaciones de datos de precipitación y descargas para la cuenca del río Mojave. La Tabla 4.9 muestra los parámetros geomorfológicos e hidrológicos calculados para la cuenca del río Mojave.
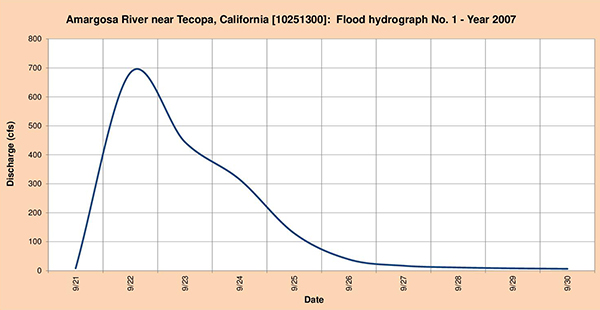
Las Figuras 4.24 de (a) hasta (c), muestran los tres (3) hidrogramas de inundación seleccionados para el análisis.
Fig. 4.24 (a) Hidrograma de inundación del río Amargosa Nro. 1 - Año 2007.
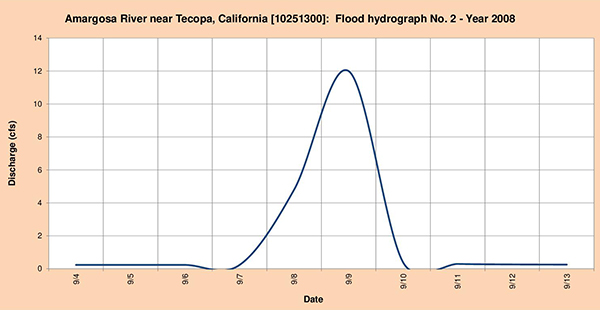
Fig. 4.24 (b) Hidrograma de inundación del río Amargosa No. 2 - Año 2008.
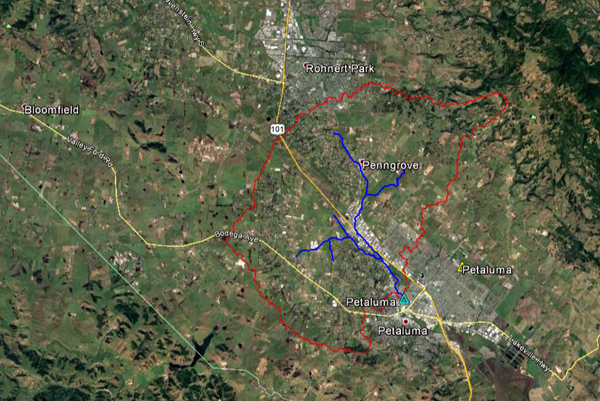
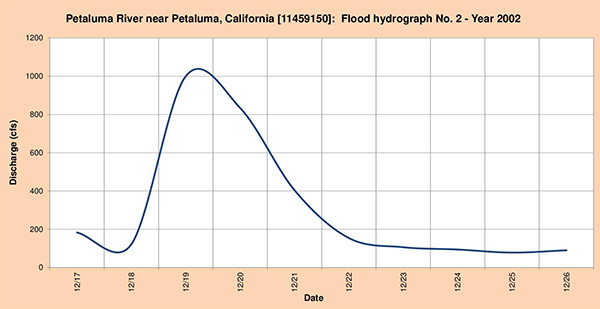
Fig. 4.24 (c) Hidrograma de inundación del río Amargosa No. 3 - Año 2010. 4.4.5 Río Petaluma en Petaluma, CA La cabecera de subcuenca del río Petaluma está localizada en las cercanías de la Montaña Sonoma. La corriente fluye predominantemente en dirección suroeste cruzando las comunidades de Penngrove y Petaluma (Fig. 4.25). La estación meteorológica del National Weather Service (NWS) está localizada en Petaluma (Fig. 4.26). La estación hidrométrica del United States Geological Service (USGS) está localizada en Petaluma.
Fig. 4.25 Río Petaluma en la ciudad de Petaluma, California.
Fig. 4.26 Estación hidrométrica del USGS en el río Petaluma.
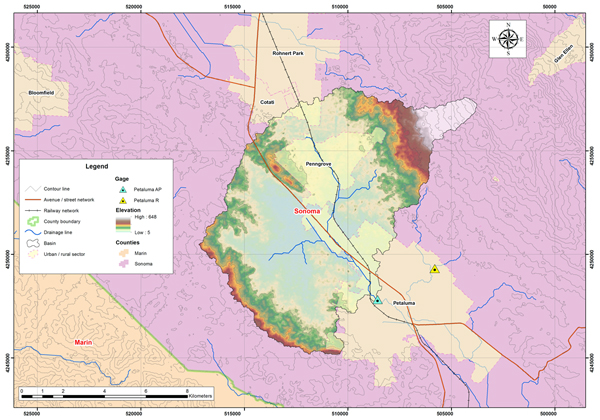
La Figura 4.27 muestra la delimitación de la subcuenca del río Petaluma. La cuenca está localizada en el condado de Sonoma en California. Según la clasificación climática de Koppen el clima es medio mediterráneo. La precipitación media anual es de 624 mm (24.57''). La Fig. 4.28 muestra el mapa hidrológico de la subcuenca del río Petaluma.
Fig. 4.27 Vista aérea de la subcuenca del río Petaluma.
Fig. 4.28 Hydrologic map of the Petaluma river basin. La Tabla 4.10 muestra la relación de estaciones de datos de precipitación y descargas para la subcuenca del río Petaluma. La Tabla 4.11 muestra los parámetros geomorfológicos e hidrológicos calculados para la subcuenca del río Petaluma.
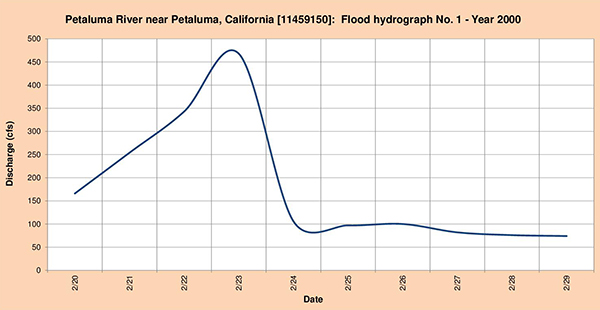
Las Figuras 4.29 de (a) hasta (c), muestran los tres (3) hidrogramas de inundación seleccionados para el análisis.
Fig. 4.29 (a) Hidrograma de inundación del río Petaluma Nro. 1 - Año 2000.
Fig. 4.29 (b) Hidrograma de inundación del río Petaluma No. 2 - Año 2002.
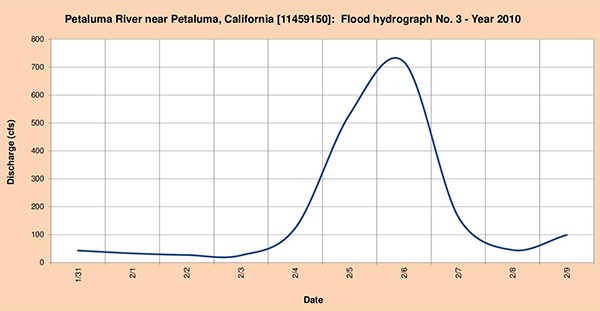
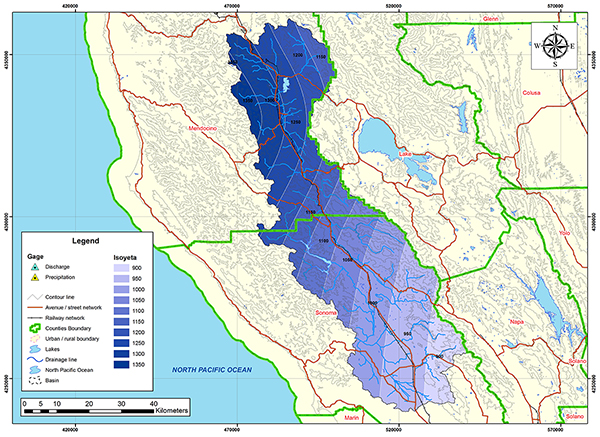
Fig. 4.29 (c) Hidrograma de inundación del río Petaluma No. 3 - Year 2010. 4.4.6 Río Russian en Guerneville, CA La cabecera de la cuenca del río Russian está localizada en las cercanías de la Montaña Santa Helena, Montaña Roja, parte alta de las comunidades de Valle Potter y Valle Redwood. La corriente fluye predominantemente en dirección sureste cruzando las comunidades de Valle Potter, Valle Redwood, Ukiah, El Roble, Largo, Hopland, Pieta, Preston, Cloverdale, Asti, Geyserville (Fig. 4.30), Healdsburg y Guerneville (Fig. 4.31). Las estaciones meteorológicas del National Weather Service (NWS) están localizadas en Valle Potter, Ukiah y Cloverdale. La estación hidrométrica del United States Geological Service (USGS) está localizado en Guerneville.
Fig. 4.30 Russian en la comunidad de Gerseyville.
Fig. 4.31 Río Russian en la comunidad de Guerneville.
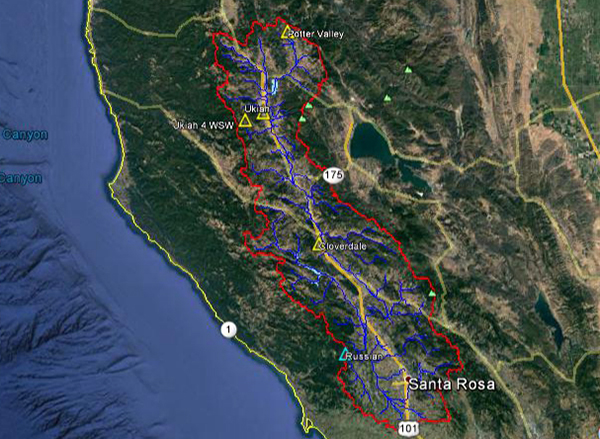
La Figura 4.22 muestra la delimitación de la cuenca del río Russian. La cuenca está localizada en los condados de Mendocino y Sonoma en California. Según la clasificación climática de Koppen se tiene un clima de verano cálido mediterráneo (Csa). La precipitación media anual es 1072 mm (42.20").
Fig. 4.32 Vista aérea de la cuenca del río Russian.
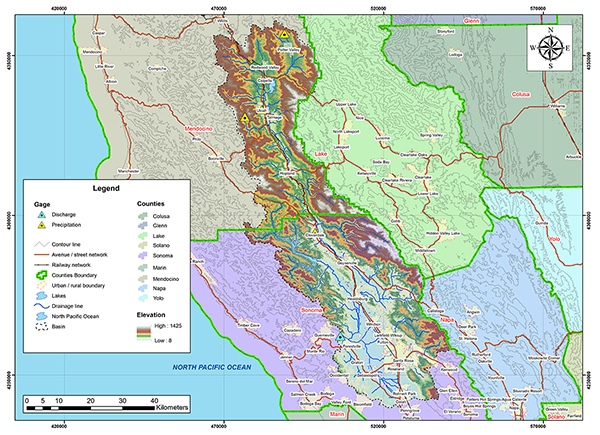
Fig. 4.33 Mapa hidrológico de la cuenca del río Russian.
Fig. 4.34 Mapa de precipitación media anual de la cuenca del río Russian. La Tabla 4.12 muestra la relación de estaciones de datos de precipitación y descargas para la cuenca del río Russian. La Tabla 4.13 muestra los parámetros geomorfológicos e hidrológicos calculados para la cuenca del río Russian.
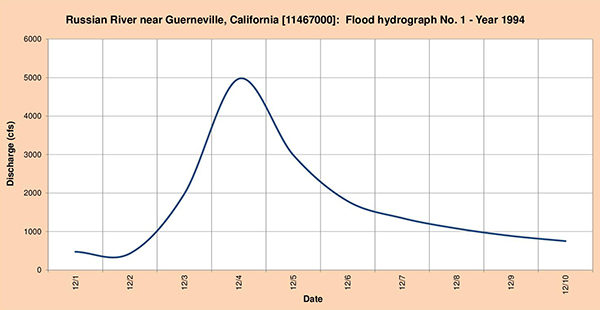
Las Figuras 4.35 (a) a (c) muestran los tres (3) hidrogramas de inundación seleccionados para el análisis.
Fig. 4.35 (a) Hidrograma de inundación del río Russian No. 1 - Año 1994.
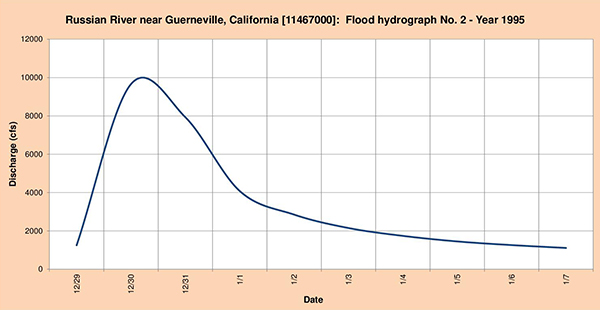
Fig. 4.35 (b) Hidrograma de inundación del río Russian No. 2 - Año 1995.
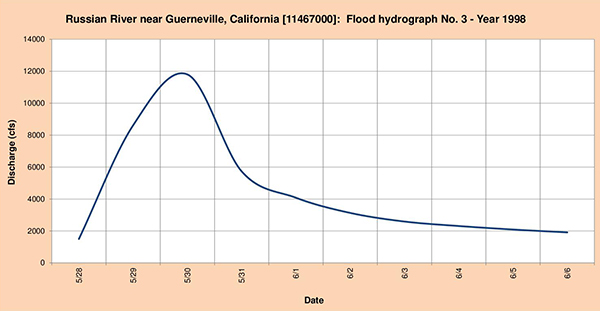
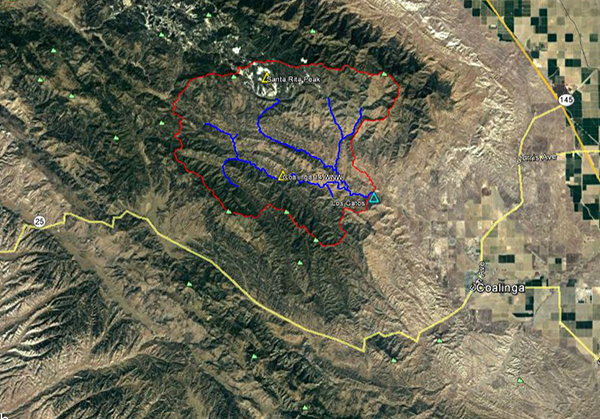
Fig. 4.35 (c) Hidrograma de inundación del río Russian No. 3 - Año 1998. 4.4.7 Quebrada Los Gatos en Coalinga, CA La cabecera de subcuenca de la quebrada Los Gatos está localizada en las cercanías del Monte Santa Rita y Monte Condone. La corriente fluye predominantemente en dirección sureste cruzando la comunidad de Coalinga (Fig. 4.36). La estación meteorológica del National Weather Service (NWS) y la estación hidrométrica del United States Geological Service (USGS) están localizadas en la comunidad de Coalinga (Fig. 4.37).
Fig. 4.36 Quebrada Los Gatos en la comunidad de Coalinga, California.
Fig. 4.37 Quebrada Los Gatos aguas arriba de la comunidad de Coalinga.
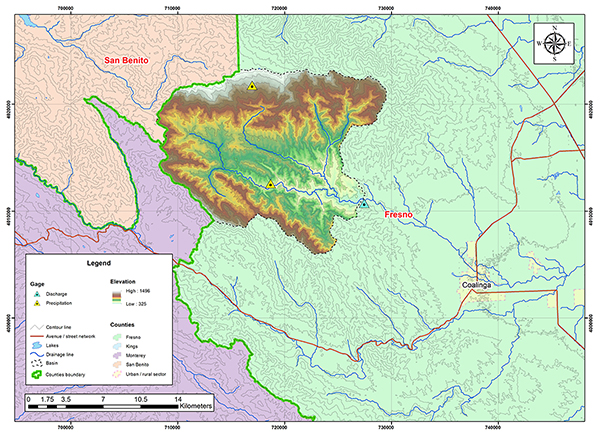
La Figura 4.38 muestra la delimitación de la subcuenca de la quebrada Los Gatos. La subcuenca está localizada en el condado de Fresno en California. Según la clasificación climática de Koppen el clima es un verano frío mediterráneo. La precipitación media anual es 394 mm (15.51").
Fig. 4.38 Vista aérea de la subcuenca de la quebrada Los Gatos.
Fig. 4.39 Mapa hidrológico de la subcuenca de la quebrada Los Gatos. La Tabla 4.14 muestra la relación de las estaciones de datos de precipitación y descarga para la subcuenca de la quebrada Los Gatos. La Tabla 4.15 muestra los parámetros geomorfológicos e hidrológicos calculados para la subcuenca de la quebrada Los Gatos.
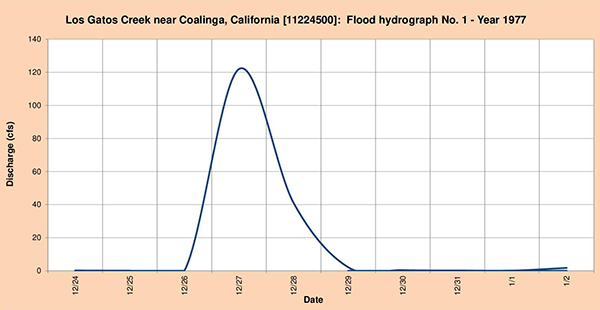
Las Figuras 4.40 (a) a (c) muestran los tres (3) hidrogramas de inundación seleccionados para el análisis
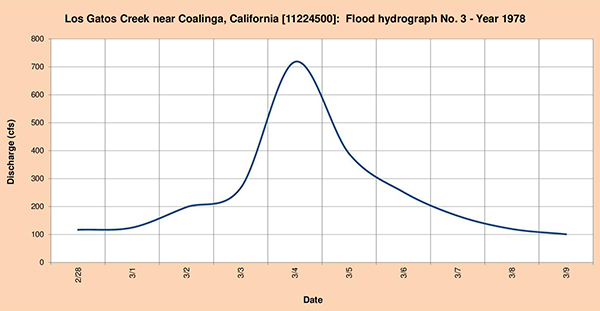
Fig. 4.40 (a) Hidrograma de inundación quebrada Los Gatos Nro. 1 - Año 1977.
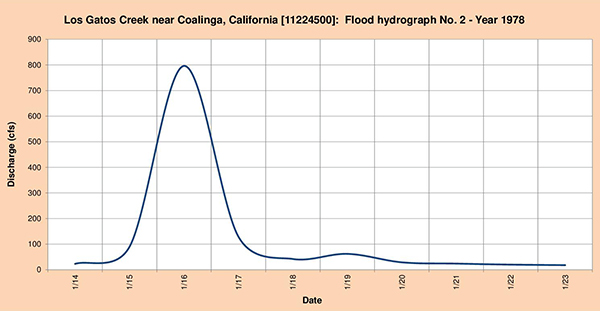
Fig. 4.40 (b) Hidrograma de inundación quebrada Los Gatos Nro. 2 - Año 1978.
Fig. 4.40 (c) Hidrograma de inundación quebrada Los Gatos Nro. 3 - Año 1978. 4.4.8 Quebrada Cottonwood en Cottonwood, CA La cabecera de cuenca de la quebrada Cottonwood está localizada en la cercanía de las zonas montañosas de las comunidades de Lazyman Butte, North Yolla Bolly y Platina. La corriente fluye predominantemente en dirección noreste cruzando las comunidades de Platina, Ono y Cottonwood (Fig. 4.41). La estación meteorológica del National Weather Service (NWS) está localizada en Platina. La estación hidrométrica del United States Geological Service (USGS) está localizado en la comunidad de Cottonwood.
Fig. 4.41 Quebrada Cottonwood en la comunidad de Cottonwood, California.
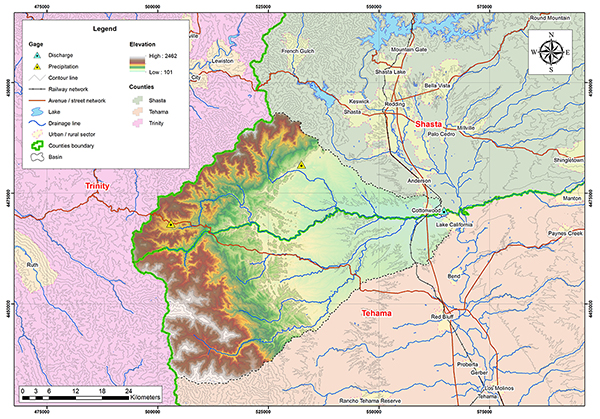
La Figura 4.42 muestra la delimitación de la cuenca de la quebrada Cottonwood. La cuenca está localizada en los condados de Shasta y Tehama en California. Según la clasificación climática de Koppen el clima es un verano templado mediterráneo (Csa). La precipitación media anual es 876 mm (34.49"). La Fig. 4.43 muestra el mapa hidrológico de la cuenca de la quebrada Cottonwood.
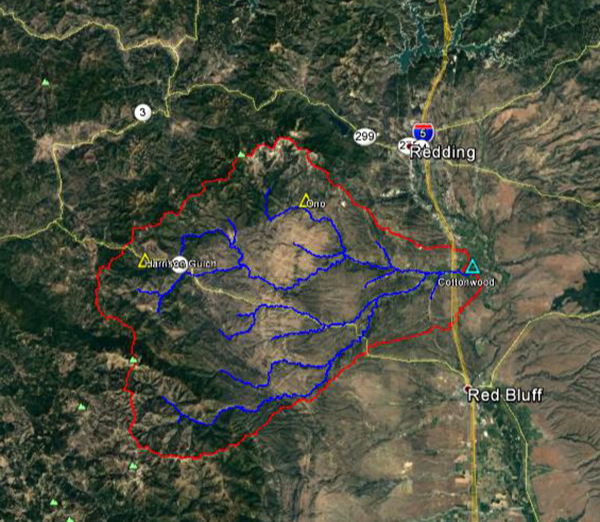
Fig. 4.42 Vista aérea de la cuenca de la quebrada Cottonwood
Fig. 4.43 Mapa hidrológico de la cuenca de la quebrada Cottonwood La Tabla 4.16 muestra la relación de las estaciones de datos de precipitación y descarga para la cuenca de la quebrada Cottonwood. La Tabla 4.17 muestra los parámetros geomorfológicos e hidrológicos calculados para la cuenca de la quebrada Cottonwood.
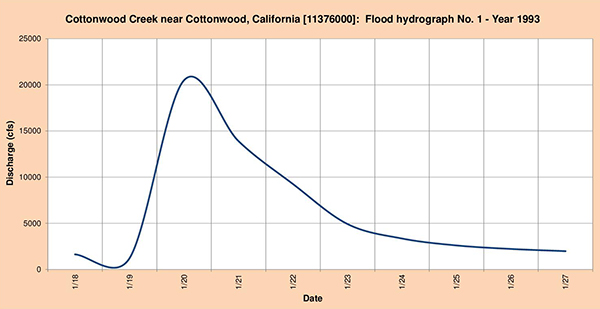
La Figura 4.44 muestra los tres (3) hidrogramas de inundación seleccionados para el análisis.
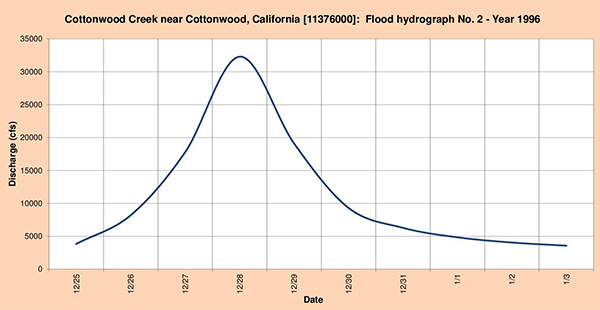
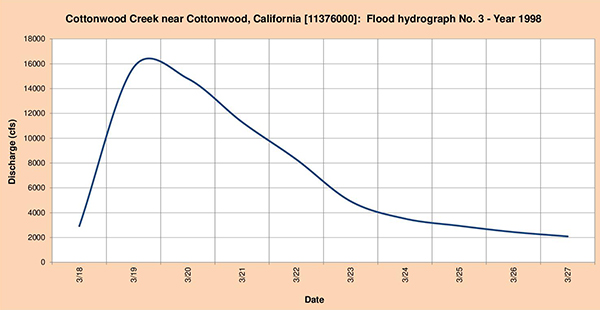
Fig. 4.44 (a) Hidrograma de inundación quebrada Cottonwood Nro. 1 Año 1993.
Fig. 4.44 (b) Hidrograma de inundación quebrada Cottonwood Nro. 2 Año 1996.
Fig. 4.44 (c) Hidrograma de inundación quebrada Cottonwood Nro. 3 Año 1998. 4.4.9 Río Salinas en Spreckels, CA
La cabecera de la cuenca del río Salinas está localizada en las cercanías de la Montaña Machesna, el Pico Tassajera, las zonas montañosas de las comunidades de Atascadero, Paso Robles, King City, Greenfield y Salinas. La corriente fluye predominantemente en dirección noreste cruzando las comunidades de San Ardo (Fotografía 4.12), Shandon, Atascadero, Paso Robles (Fotografía 4.13), San Miguel, Bradley, San Lucas, King City, Greenfield, Soledad, Gonzales, Chualar y Salinas.
Fig. 4.45 Río Salinas en la comunidad de San Ardo, California.
Fig. 4.46 Río Salinas en la comunidad de Paso Robles, California.
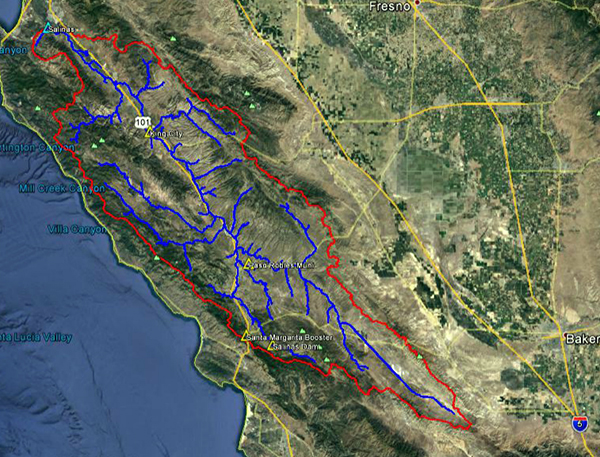
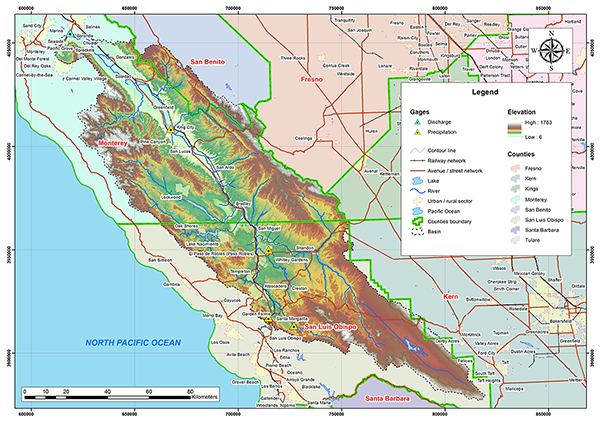
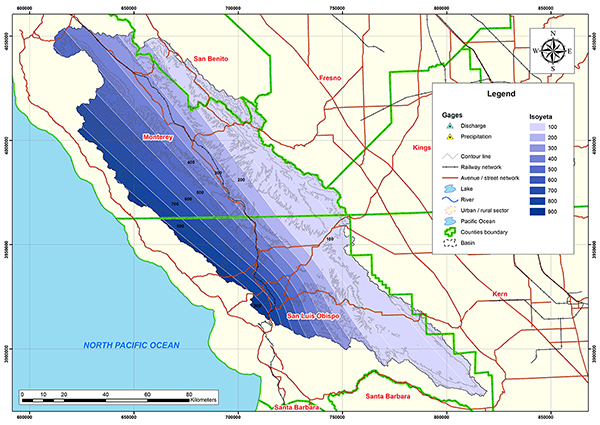
La Figura 4.47 muestra la delimitación de la cuenca del río Salinas. La cuenca está localizada en los condados de San Luis Obispo, Monterrey y San Benito en California. Según la clasificación de Koppen el clima es semiárido y seco mediterráneo (Csb).
La precipitación media anual es 294 mm (11.57''). La Figura 4.48 y 4.49 muestran el mapa hidrológico y el mapa de precipitación media anual de la cuenca del río Salinas.
Fig. 4.47 Vista aérea de la cuenca del río Salinas.
Fig. 4.48 Mapa hidrológico de la cuenca del río Salinas.
Fig. 4.49 Mapa de precipitación media anual de la cuenca del río Salinas. La Tabla 4.18 muestra la relación de las estaciones de datos de precipitación y descarga para la cuenca del río Salinas. La Tabla 4.19 muestra los parámetros geomorfológicos e hidrológicos calculados para la cuenca del río Salinas.
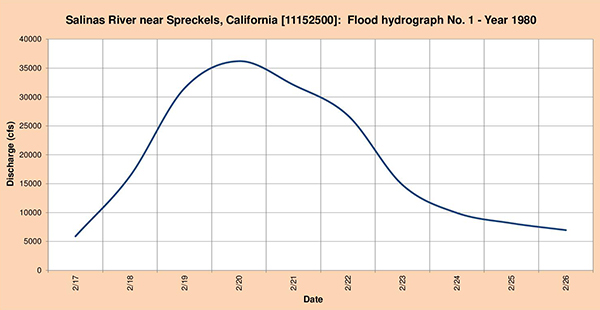
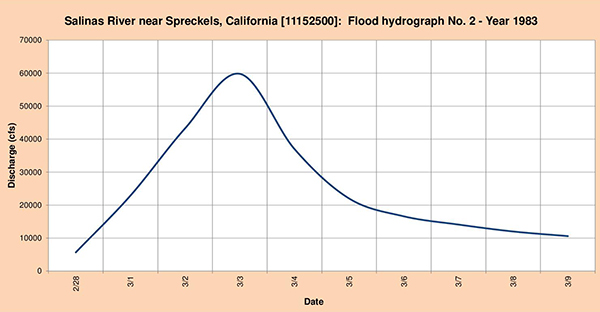
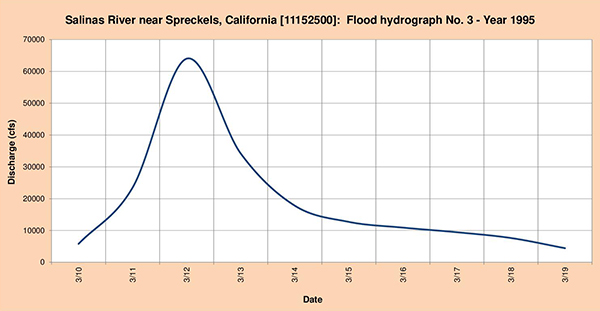
La Figura 4.50 muestra los tres (3) hidrogramas de inundación seleccionados para el análisis.
Fig. 4.50 (a) Hidrograma de inundación del río Salinas Nro. 1 Año 1980.
Fig. 4.50 (b) Hidrograma de inundación del río Salinas Nro. 2 Año 1983.
Fig. 4.50 (c) Hidrograma de inundación del río Salinas Nro. 3 Año 1995. 4.4.10 Río Shasta en Montague, CA
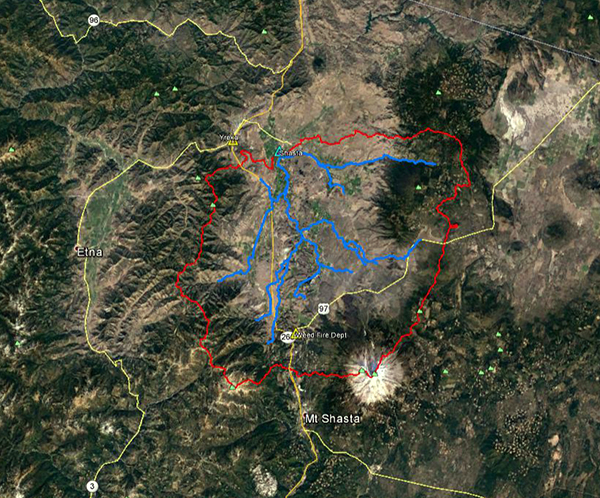
La cabecera de la cuenca del río Shasta está localizada en las cercanías de la Montaña Shasta y de la Montaña China. La corriente fluye predominantemente en dirección noreste cruzando la comunidad de Edgewood (Fig. 4.51), Gazelle, Grenada y Montague (Fig. 4.52).
La estación meteorológica del National Weather Service (NWS) Está localizada en la comunidad de Weed.
Fig. 4.51 Río Shasta cerca de Edgewood, California.
Fig. 4.52 Río Shasta en la comunidad de Montague, California.
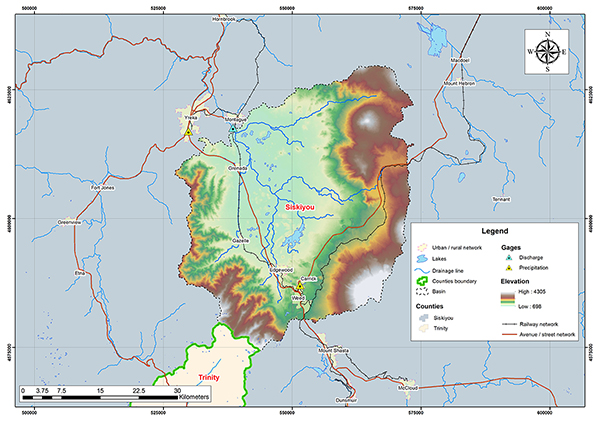
La Figura 4.53 muestra la delimitación de la cuenca del río Shasta. La cuenca está localizada en el condado de Siskiyou en California. Según la clasificación Koppen se tiene un clima verano templado mediterráneo. La precipitación media anual es 478 mm (18.82''). La Fig. 4.40 muestra el mapa hidrológico de la cuenca del río Shasta.
Fig. 4.53 Vista aérea de la cuenca del río Shasta.
Fig. 4.54 Vista aérea de la cuenca del río Shasta. La Tabla 4.20 muestra la relación de las estaciones de datos de precipitación y descarga para la cuenca del río Shasta. la Tabla 4.21 muestra los parámetros geomorfológicos e hidrológicos calculados para la cuenca del río Shasta.
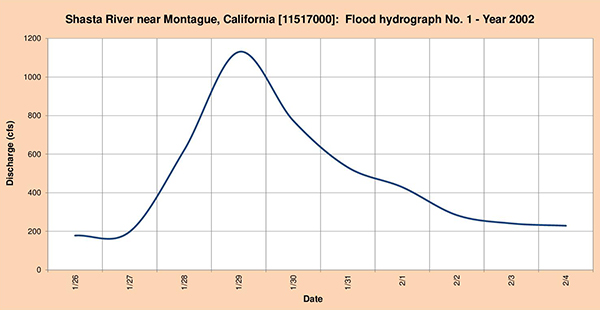
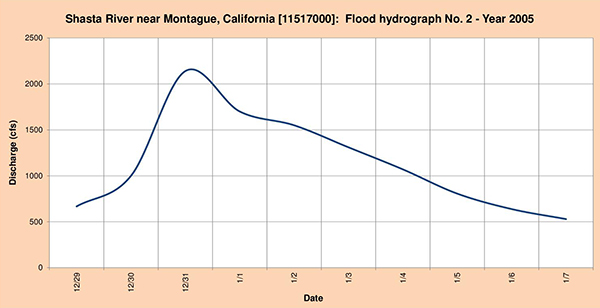
La Figura 4.55 muestran los tres (3) hidrogramas de inundación seleccionados para el análisis.
Fig. 4.55 (a) Hidrograma de inundación del río Shasta Nro. 1 Año 2002.
Fig. 4.55 (b) Hidrograma de inundación del río Shasta Nro. 2 Año 2005.
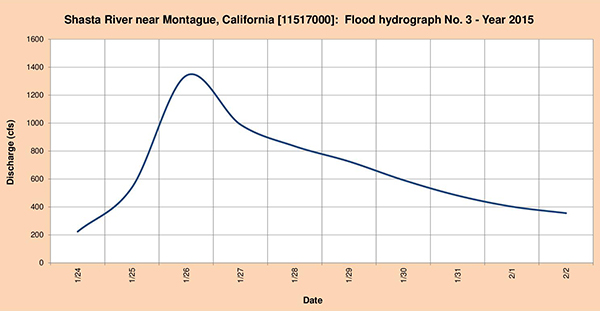
Fig. 4.55 (c) Hidrograma de inundación del río Shasta Nro. 3 Año 2015.
5. APLICACIÓN DEL MODELO HUAG
5.1 Análisis de datos Siguiendo la Sección 3, el análisis de datos puede basarse en: (a) tormentas simples, o (b) tormentas complejas. Para la mayor parte, la calidad de los datos impidió la aplicación del análisis de tormentas complejas. En consecuencia, las tormentas simples fueron elegidas como un compromiso práctico para la aplicación general. Se escogieron tres (3) conjuntos de eventos de datos de precipitación-escorrentía correspondientes a cada cuenca. Los resultados del ejemplo a la quebrada Campo, se muestran en las Tablas 5.1 y 5.2. La Tabla 5.1 muestra lo siguiente:
La Tabla 5.2 muestra lo siguiente:
5.1.1 Quebrada Campo
Siguiendo el procedimiento descrito en la Sección 3.1.1, los tres (3) grupos de eventos correspondientes a la información de precipitación-escorrentía fueron reunidos para la subcuenca de la quebrada Campo. Los resultados se resumen en las Tablas 5.3 y 5.4.
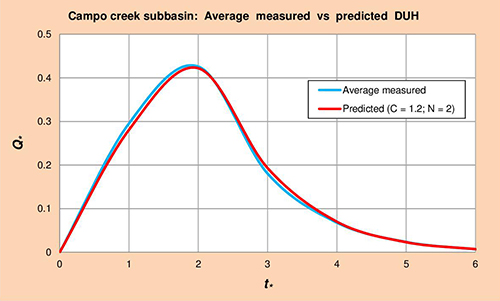
La Figura 5.1 muestra los hidrogramas unitarios promedio medido vs. Predicho (HUA) para la subcuenca de la quebrada Campo, obtenido por método gráfico de la Col. 1 vs. Cols. 5 y 6 de la Tabla 5.4, respectivamente.
Fig. 5.1 Subcuenca de la quebrada Campo: Promedio medido vs. Predicho HUA. 5.1.2 Río Whitewater
Siguiendo el procedimiento descrito en la Sección 3.1.2, los tres (3) grupos de eventos correspondientes a la información de precipitación-escorrentía fueron reunidos para la cuenca del río Whitewater. Los resultados se resumen en las Tablas 5.5 y 5.6.
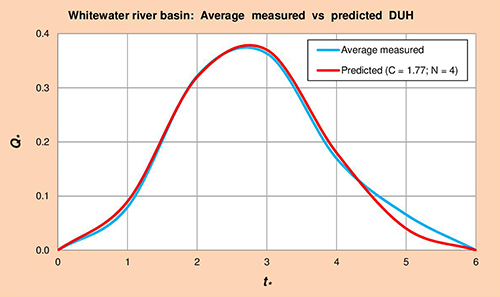
La Figura 5.2 muestra los hidrogramas unitarios promedio medido vs. Predicho (HUA) para la cuenca del río Whitewater, obtenido por método gráfico de la Col. 1 vs. Cols. 5 y 6 de la Tabla 5.6, respectivamente.
Fig. 5.2 Cuenca del río Whitewater: Promedio medido vs. Predicho HUA. 5.1.3 Río Mojave
Siguiendo el procedimiento descrito en la Sección 3.1.3, los tres (3) grupos de eventos correspondientes a la información de precipitación-escorrentía fueron reunidos para la cuenca del río Mojave. Los resultados se resumen en las Tablas 5.7 y 5.8.
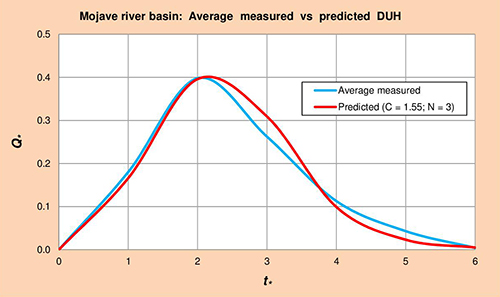
La Figura 5.3 muestra los hidrogramas unitarios promedio medido vs. Predicho (HUA) para la cuenca del río Mojave, obtenido por método gráfico de la Col. 1 vs. Cols. 5 y 6 de la Tabla 5.8, respectivamente.
Fig. 5.3 Cuenca del río Mojave: Promedio medido vs. Predicho HUA. 5.1.4 Río Amargosa
Siguiendo el procedimiento descrito en la Sección 3.1.4, los tres (3) grupos de eventos correspondientes a la información de precipitación-escorrentía fueron reunidos para la cuenca del río Amargosa. Los resultados se resumen en las Tablas 5.9 y 5.10.
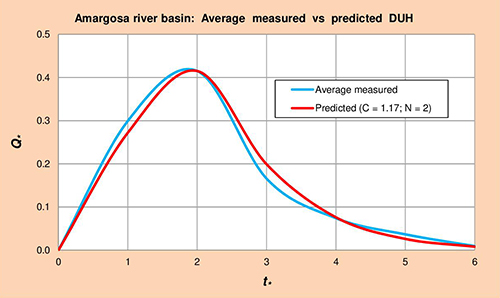
La Figura 5.4 muestra los hidrogramas unitarios promedio medido vs. Predicho (HUA) para la cuenca del río Amargosa, obtenido por método gráfico de la Col. 1 vs. Cols. 5 y 6 de la Tabla 5.10, respectivamente.
Fig. 5.4 Cuenca del río Amargosa: Promedio medido vs. Predicho HUA. 5.1.5 Río Petaluma
Siguiendo el procedimiento descrito en la Sección 3.1.5, los tres (3) grupos de eventos correspondientes a la información de precipitación-escorrentía fueron reunidos para la subcuenca del río Petaluma. Los resultados se resumen en las Tablas 5.11 y 5.12.
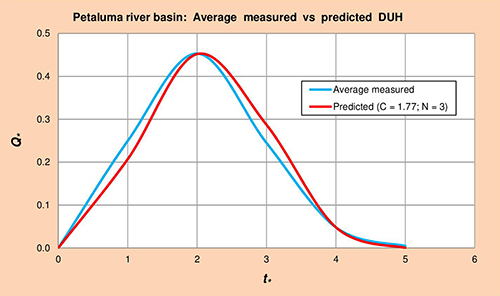
La Figura 5.5 muestra los hidrogramas unitarios promedio medido vs. Predicho (HUA) para la subcuenca del río Petaluma, obtenido por método gráfico de la Col. 1 vs. Cols. 5 y 6 de la Tabla 5.12, respectivamente.
Fig. 5.5 Subcuenca del río Petaluma: Promedio medido vs. Predicho HUA. 5.1.6 Río Russian
Siguiendo el procedimiento descrito en la Sección 3.1.6, los tres (3) grupos de eventos correspondientes a la información de precipitación-escorrentía fueron reunidos para la cuenca del río Russian. Los resultados se resumen en las Tablas 5.13 y 5.14.
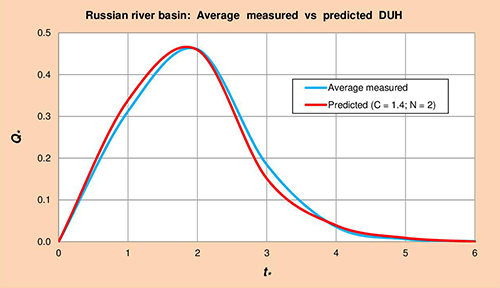
La Figura 5.6 muestra los hidrogramas unitarios promedio medido vs. Predicho (HUA) para la cuenca del río Russian, obtenido por método gráfico de la Col. 1 vs. Cols. 5 y 6 de la Tabla 5.14, respectivamente.
Fig. 5.6 Cuenca del río Russian: Promedio medido vs. Predicho HUA. 5.1.7 Quebrada Los Gatos
Siguiendo el procedimiento descrito en la Sección 3.1.7, los tres (3) grupos de eventos correspondientes a la información de precipitación-escorrentía fueron reunidos para la subcuenca de la quebrada Los Gatos. Los resultados se resumen en las Tablas 5.15 y 5.16.
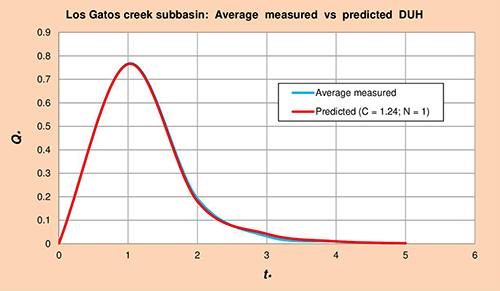
La Figura 5.7 muestra los hidrogramas unitarios promedio medido vs. Predicho (HUA) para la subcuenca de la quebrada Los Gatos, obtenido por método gráfico de la Col. 1 vs. Cols. 5 y 6 de la Tabla 5.16, respectivamente.
Fig. 5.7 Subcuenca de la quebrada Los Gatos: Promedio medido vs. Predicho HUA. 5.1.8 Quebrada Cottonwood
Siguiendo el procedimiento descrito en la Sección 3.1.8, los tres (3) grupos de eventos correspondientes a la información de precipitación-escorrentía fueron reunidos para la cuenca de la quebrada Cottonwood. Los resultados se resumen en las Tablas 5.17 y 5.18.
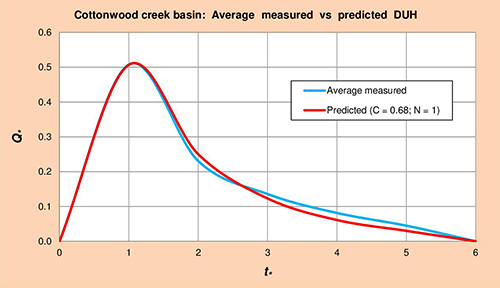
La Figura 5.8 muestra los hidrogramas unitarios promedio medido vs. Predicho (HUA) para la cuenca de la quebrada Cottonwood, obtenido por método gráfico de la Col. 1 vs. Cols. 5 y 6 de la Tabla 5.18, respectivamente.
Fig. 5.8 Cuenca de la quebrada Cottonwood: Promedio medido vs. Predicho HUA. 5.1.9 Río Salinas
Siguiendo el procedimiento descrito en la Sección 3.1.9, los tres (3) grupos de eventos correspondientes a la información de precipitación-escorrentía fueron reunidos para la cuenca del río Salinas. Los resultados se resumen en las Tablas 5.19 y 5.20.
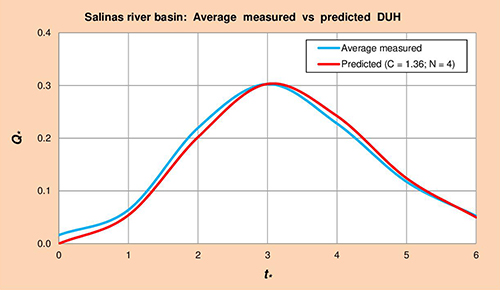
La Figura 5.9 muestra los hidrogramas unitarios promedio medido vs. Predicho (HUA) para la cuenca del río Salinas, obtenido por método gráfico de la Col. 1 vs. Cols. 5 y 6 de la Tabla 5.20, respectivamente.
Fig. 5.9 Cuenca del río Salinas: Promedio medido vs. Predicho HUA. 5.1.10 Río Shasta
Siguiendo el procedimiento descrito en la Sección 3.1.10, los tres (3) grupos de eventos correspondientes a la información de precipitación-escorrentía fueron reunidos para la cuenca del río Shasta. Los resultados se resumen en las Tablas 5.21 y 5.22.
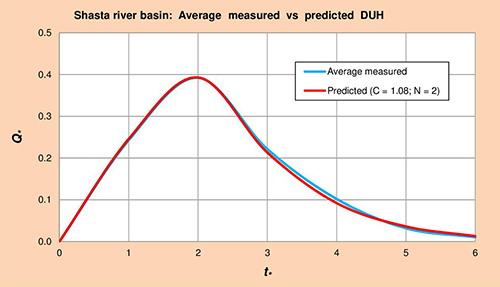
La Figura 5.10 muestra los hidrogramas unitarios promedio medido vs. Predicho (HUA) para la cuenca del río Shasta, obtenido por método gráfico de la Col. 1 vs. Cols. 5 y 6 de la Tabla 5.22, respectivamente.
Fig. 5.10 Cuenca del río Shasta: Promedio medido vs. Predicho HUA. 5.2 Análisis de resultados
Para propósito ilustrativo, la Fig. 5.7 se repite aquí. Dónde se demuestra que los diez (10) casos estudiados (Sección 5.1) tienen una excelente concordancia entre el HUA promedio medido y el HUA Predicho.
Por lo tanto, la metodología presentada en la Sección 3 puede ser utilizada para calcular los parámetros de la CRL con una expectativa razonable de precisión, considerando datos correspondientes a precipitación y escorrentía.
En la práctica, tres eventos de poca frecuencia de precipitación-escorrentía con características de hidrogramas similares pueden ser utilizados para desarrollar el HUA promedio medido, del que se puede obtener el HUA Predicho. No obstante, la incertidumbre puede verse afectada para el caso donde los eventos seleccionados presenten características de hidrogramas muy diferentes.
Fig. 5.7 Subcuenca de la quebrada Los Gatos: Promedio medido vs. Predicho HUA. 5.3 Análisis Geomorfológico En esta sección, los parámetros geomorfológicos medidos descritos en la Sección 4.3, están relacionados con los parámetros de la CRL descritos en la Sección 5.1. En la Tabla 5.23 se muestra lo siguiente:
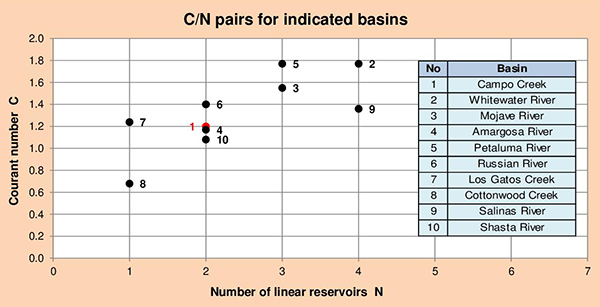
La Figura 5.11 muestra los pares calculados de C/N para las cuencas estudiadas. En general, un valor inferior de N (N = 1) corresponde a una cuenca de pendiente pronunciada (No. 7 y 8), mientras que un valor superior de N (N = 4) corresponde a una cuenca de pendiente más suave (No. 2, 3 y 9). Como se muestra en la Sección 3.4, la difusión del hidrograma incrementa con el número de reservorios lineales.
Fig. 5.11 Pares de C/N para las cuencas estudiadas.
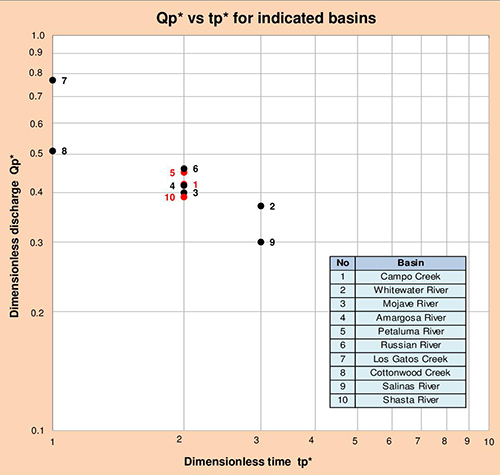
La Figura 5.12 muestra la relación entre la descarga pico Qp* y el tiempo pico tp* del hidrograma unitario adimensional (HUA) para las diez (10) cuencas estudiadas. Este gráfico demuestra que un incremento de la difusión del hidrograma se da con un decrecimiento de la pendiente del canal principal (comparar No. 7 y No. 9).
Fig. 5.12 Qp* vs tp* para las cuencas estudiadas. 5.4 Modelamiento de la Difusión del Hidrograma Unitario
La Sección 3.4 muestra que la difusión del hidrograma incrementa con el aumento del valor de N y el decrecimiento del valor de C. Por lo tanto, un número de difusión D puede ser definido a continuación:
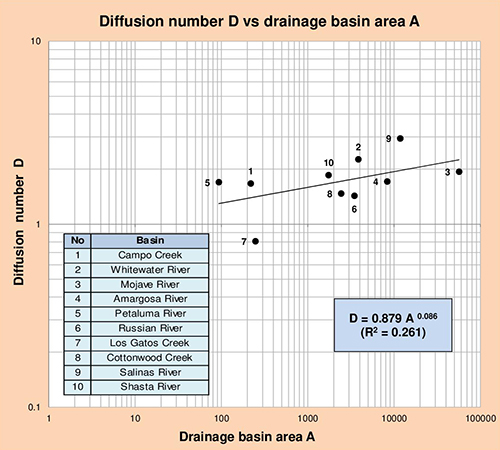
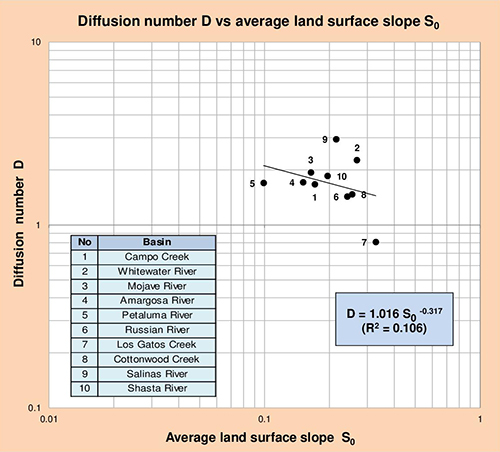
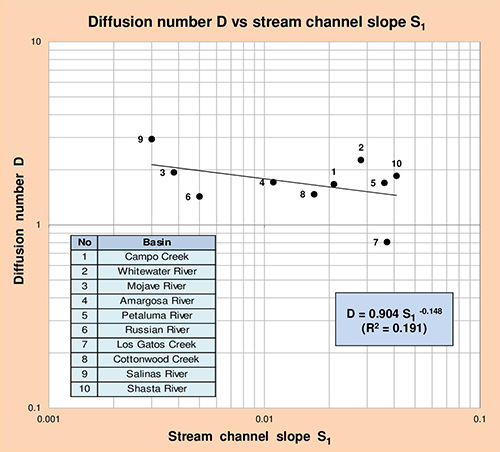
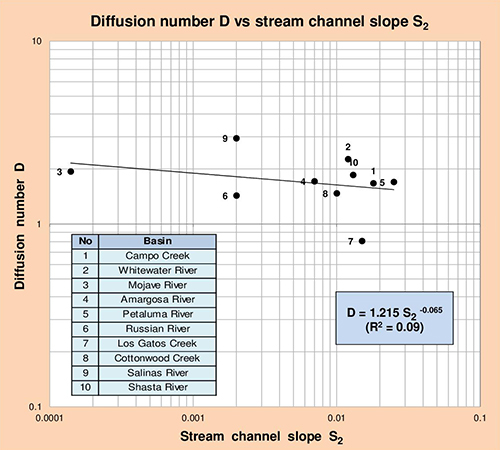
Las Figuras 5.13 a 5.16 muestran la correlación del número de difusión D con los parámetros geomorfológicos pertinentes: (1) área de drenaje de la cuenca A, (2) pendiente promedio de la superficie del terreno S0, (3) pendiente del canal principal S1, y (4) pendiente del canal principal S2 (referido a la Tabla 5.23). Los resultados de estas correlaciones se resumen en la Tabla 5.24.
Fig. 5.13 Número de difusión D vs Área de drenaje de la cuenca A.
Fig. 5.14 Número de difusión D vs Pendiente promedio de la superficie del terreno S0.
Fig. 5.15 Número de difusión D vs Pendiente del canal principal S1.
Fig. 5.16 Número de difusión D vs Pendiente del canal principal S2.
La Tabla 5.24 demuestra que el número de difusión D se correlaciona razonablemente bien con el área de drenaje de la cuenca A, y en menor medida con la pendiente del canal principal S1. En una aplicación práctica, considerando un valor de A o S1, las correlaciones mostradas en esta tabla pueden ser utilizadas para calcular el número de difusión D.
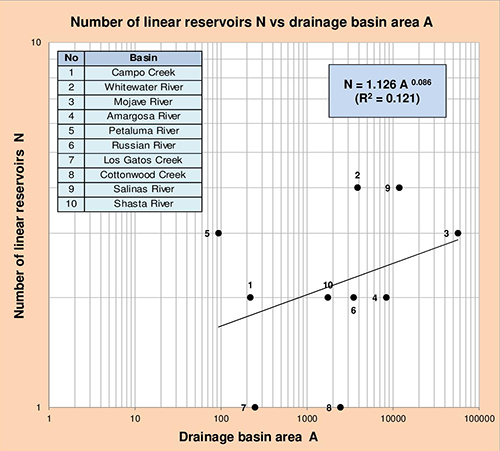
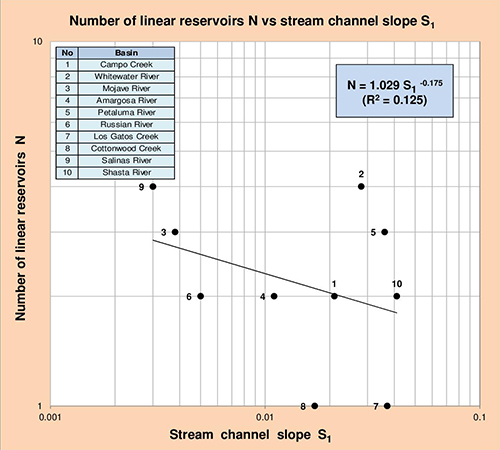
Las Figuras 5.17 y 5.18, muestran la correlación del número de reservorios lineales N con los siguientes parámetros geomorfológicos: (1) área de drenaje de la cuenca A, y (2) canal principal de la cuenca S1. Dado un valor de A o S1, la correlación mostrada puede utilizarse para calcular N.
Fig. 5.17 Número de reservorios lineales N vs Área de drenaje de la cuenca A.
Fig. 5.18 Número de reservorios lineales N vs Pendiente del canal principal S1.
6. CONCLUSIONES Y RECOMENDACIONES
6.1 Resumen La investigación validó la teoría del hidrograma unitario adimensional general (HUAG) utilizando información de cuencas de California. El HUAG es una formulación adimensional del concepto del hidrograma unitario, de aplicabilidad general y de alcance global. Considerando un área de drenaje de cuenca A, para la cual se busca un hidrograma unitario de duración tr, la metodología del HUAG nos proporciona un hidrograma unitario adimensional (HUA) que se basa en los parámetros de la cascada de reservorios lineales (CRL) como C y N, donde C = número de Courant y N = número de reservorios lineales en serie. La metodología está basada en comparar un HUA promedio medido con un HUA Predicho. Se seleccionaron diez (10) cuencas sustentables en California, cubriendo un rango amplio de parámetros geomorfológicos como el área de drenaje, la pendiente promedio de la superficie del terreno, y la pendiente principal del canal. Se escogieron tres (3) eventos de poca frecuencia de inundación, dando lugar a tres (3) hidrogramas unitarios, de los cuales se obtuvo un HUA promedio medido. Utilizando el modelo de la CRL, un HUA Predicho, con parámetros C y N, fue calculado por prueba y error para ser comparado con un HUA promedio medido. Se definió un parámetro de difusión D para ayudar en el modelamiento de la difusión del hidrograma unitario. Dado que este último aumenta con el incremento del valor de N y un decrecimiento en C, una primera aproximación D fue tomada como: D = N /C. Las correlaciones entre D y los parámetros geomorfológicos sustentados indicaron que existe un buen ajuste no lineal razonable entre el parámetro D y: (a) área de drenaje A, y (b) pendiente del canal principal S1. Adicionalmente, se realizó una correlación entre el número de reservorios lineales N y: (a) área de drenaje A, y (b) pendiente del canal principal S1. Estas dos (2) correlaciones permitieron el cálculo de la duración tr del hidrograma unitario para una cuenca definida de área de drenaje A. La metodología desarrollada en esta investigación proporciona una manera de vincular la forma del hidrograma unitario, es decir, la cantidad de la difusión de su escorrentía, con las características geomorfológicas de la cuenca. Es notorio que este objetivo ha sido el centro de la investigación del hidrograma unitario durante muchas décadas. Aplicaciones adicionales en todo el mundo podrían proporcionar más información para fortalecer las correlaciones más allá de este primer intento de validación de la teoría del HUAG. 6.2 Conclusiones Las siguientes conclusiones son derivadas de este estudio:
6.3 Recomendaciones Las siguientes recomendaciones son ofrecidas para futuras investigaciones:
BIBLIOGRAFÍA
Dooge, J. C. I. (1973). Linear theory of hydrologic systems. Technical Bulletin No. 1468, Agricultural Research Service, U.S. Department of Agriculture, Washington, D.C. http://ponce.sdsu.edu/lineartheo232.html
Dooge, J. C. I., W. B. Strupczewski, y J. J. Napiorkowski (1982). Hydrodynamic derivation of storage parameters of the Muskingum model. Journal of Hydrology, Vol. 54, 371-387. http://ponce.sdsu.edu//dooge_hydrodynamic_derivation_1982.pdf
Hayami, S. (1951). On the propagation of flood waves. Bulletin No. 1, Disaster Prevention Research Institute, Kyoto University, Kyoto, Japan, December. http://ponce.sdsu.edu/milestone_hayami_first_page.html
Hoyt, W. G. et. al. (1936). Studies of relations of rainfall and runoff in the United States, Lighthill, M. J., y G. B. Whitham. (1955). On kinematic waves: I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316. http://ponce.sdsu.edu/lighthillandwhitham281.html
Linsley, R. K., M. A. Kohler, y L. H. Paulhus. (1962). Hydrology for Engineers, Third edition, McGraw-Hill, New York.
Nash, J. E. (1957). The form of the instantaneous unit hydrograph, Ponce, V. M., y D. B. Simons (1977). Shallow wave propagation in open channel flow. Ponce, V. M. (1980). Linear reservoirs and numerical diffusion. Journal of the Hydraulics Division, Proceedings of the American Society of Civil Engineers, Vol. 106, No. HY5, 691-699. Ponce, V. M. (1989). Engineering hydrology, principles and practices, Prentice Hall, Englewood Cliffs, New Jersey. http://ponce.sdsu.edu/textbook_hydrology_chapters.html
Ponce, V. M. (1991a). The kinematic wave controversy. Journal of Hydraulic Engineering, ASCE, Vol. 117, No. 4, 511-525, April. http://ponce.sdsu.edu/the_kinematic_wave_controversy.html
Ponce, V. M. (1991b). New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July. http://ponce.sdsu.edu/new_perspective_on_the_vedernikov_number.html
Ponce, V. M., O. I. Cordero-Braña, y S. Y. Hasenin (1997). Generalized conceptual modeling of dimensionless overland flow hydrographs. Journal of Hydrology, 200, 222-227. http://ponce.sdsu.edu/generalized_conceptual_modeling_of_dimensionless_overland_flow_hydrographs.html
Ponce, V. M., y A. C. Klabunde (1999). Parking lot storage modeling using diffusion waves. Journal of Hydrologic Engineering, Vol. 4, No. 4, October, 371-376. http://ponce.sdsu.edu/parkinglot371view.html
Ponce, V. M. (2009a). A general dimensionless unit hydrograph. Online report.
Ponce, V. M. (2009b). Cascade and convolution: One and the same. Online report.
http://ponce.sdsu.edu//cascade_and_convolution.html
Ponce, V. M. (2014a). Engineering hydrology, principles and practices, Second Edition, Online.
http://ponce.sdsu.edu/enghydro/
Ponce, V. M. (2014b). Runoff diffusion reexamined. Online report.
http://ponce.sdsu.edu/runoff_diffusion_reexamined.html
Sherman, L. K. (1932). Streamflow from rainfall by unit-graph method, Rodríguez-Iturbe, I. y J. B. Valdés. (1979). The geomorphologic structure of hydrologic response. Water Resources Research, Vol. 15, No. 6, 1409-1420. Rodríguez-Iturbe, I.; G. Devoto, y J. B. Valdés. (1979). Discharge response analysis and hydrologic similarity: the interrelation between the geomorphologic IUH and the storms characteristics. Water Resources Research, Vol. 15, No. 6, 1435-1444. U.S. Army Engineer North Pacific Division. (1972). Program Description and User Manual for SSARR Model, Streamflow Synthesis and Reservoir Regulation, revised June 1975, Portland, Oregon.
Valdés, J. B., Y. Fiallo, y I. Rodríguez-Iturbe. (1979). A rainfall-runoff analysis of the geomorphologic IUH. Water Resources Research, Vol. 15, No. 6, 1421-1434.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||