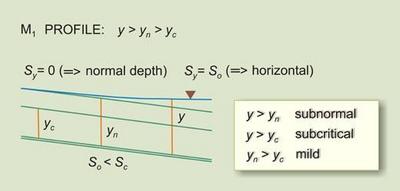
Las curvas de remanso se expresan en términos de la pendiente crítica Sc .
De esta manera, se demuestra que la gradiente de profundidad dy/dx
está físicamente limitada a valores fuera del rango comprendido entre Sc y la
pendiente de fondo So.
Este nueva formulación mejora y completa la definición de rangos de gradiente de profundidad en el análisis de
curvas de remanso. Adicionalmente, se presentan calculadores en línea para las curvas de remanso.
1. INTRODUCCIÓN El cálculo del flujo gradualmente variado es parte de la práctica de la ingeniería hidráulica. La ecuación convencional del flujo gradualmente variado se expresa en función de la pendiente de fondo So, la pendiente de fricción Sf, y el número de Froude F (Chow 1959; Henderson 1966). En este trabajo, la ecuación de flujo gradualmente variado se expresa alternativamente en función de la pendiente de fondo So , la pendiente crítica Sc , y el número de Froude F. El examen de esta ecuación revela que el gradiente de profundidad dy/dx está limitado a valores fuera del rango comprendido entre So y Sc . Este análisis mejora y completa la definición de rangos de gradiente de profundidades en las curvas de remanso. 2. ECUACIÓN DEL FLUJO GRADUALMENTE VARIADO La ecuación de flujo gradualmente variado es (Chow 1959, página 220; Henderson 1966, página 130):
en la cual y = profundidad, x = distancia a lo largo del canal, dy/dx = gradiente de profundidad, Q = caudal o descarga, T = ancho de la superficie libre, A = área de flujo, y g = aceleración de la gravedad. Esta ecuación es válida para pendientes pequeñas (So < 0.1), lo cual es el caso típico. La pendiente de fricción en términos del coeficiente de Chezy C es (Chow 1959):
en la cual R = A/P = radio hidráulico, and P = perímetro mojado, El número de Froude en términos de descarga Q es (Chow 1959):
Combinando las ecuaciones 2 y 3 se obtiene:
En el flujo normal crítico F = 1, y la pendiente de fricción para el flujo crítico, es decir, la pendiente crítica, es:
Combinando las ecuaciones 1, 4, y 5:
la cual es estrictamente válida para la siguiente condición: P /T = Pc /Tc . Esta última condición se satisface en un canal hidráulicamente ancho, para el cual T es asintóticamente igual a P.
Para mayor facilidad de expresión, la gradiente de profundidad se redefine como Sy = dy/dx. Resolviendo la ecuación 6 para el número de Froude:
Tomando en cuenta que F 2 > 0, la gradiente de profundidad debe satisfacer las siguientes desigualdades:
lo cual limita la gradiente de profundidad Sy a valores fuera del rango comprendido entre So y Sc . Además, la ecuación 6 puede ser alternativamente expresada como sigue:
La ecuación 10 es la ecuación de flujo permanente gradualmente variado expresada en términos de la pendiente de fondo So , la pendiente crítica Sc , y el número de Froude F. La pendiente de fondo podría ser positiva (supercrítica, crítica, o subcrítica), cero (horizontal), o negativa (adversa). La pendiente crítica (Ecuación 5) y el número de Froude (Ecuación 3) son siempre positivos. 3. CLASIFICACIÓN DE LAS CURVAS DE REMANSO
La ecuación 10 se utiliza para desarrollar una clasificación de curvas de remanso
basada solamente en los tres parámetros adimensionales:
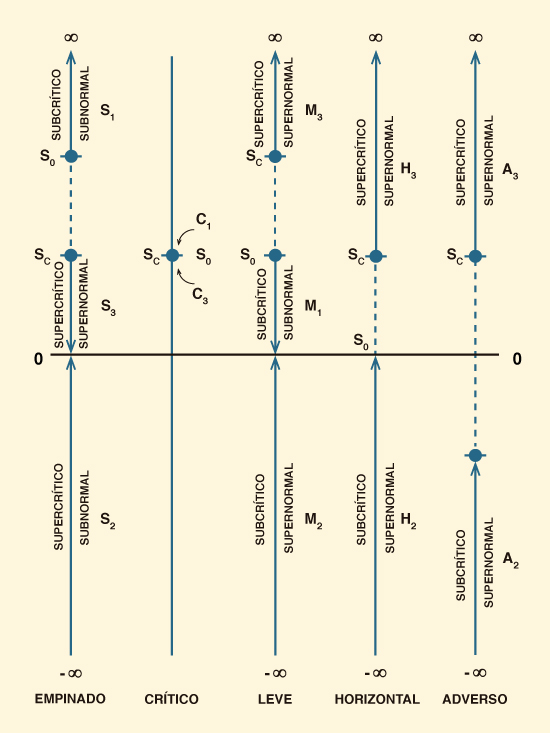
El Cuadro 2 muestra un resumen de los tipos posibles de las curvas de remanso.
La clasificación se obtiene directamente de la ecuación de flujo permanente gradualmente variado (Ecuación 10).
Se observa que el tipo de perfil (Tipo 1, 2, o 3)
determina el signo de
Contrariamente a la información disponible en las referencias tradicionales (Chow 1959; Henderson 1966), los rangos de gradiente de profundidad (Cuadro 2, Columnas 7 y 8) están ahora completos para los doce (12) perfiles de curvas de remanso. En forma significativa, se nota que la gradiente de profundidad Sy está fuera del rango comprendido entre Sc y So . La Figura 1 muestra una representación gráfica de los rangos del gradiente de profundidad. La flecha indica la dirección del cálculo. Por ejemplo, el gradiente de profundidad para el perfil S3 (supercrítico/supernormal) decrece de Sc (un valor finito positivo) a 0 (asintótico al flujo normal). De igual manera, el gradiente de profundidad para los perfiles C1 (subcrítico/subnormal) y C3 (supercrítico/supernormal) es constante e igual a So = Sc . El Cuadro 2 contiene enlaces para accesar los respectivos calculadores en línea para las doce (12) curvas de remanso.
en las curvas de remanso. 4. RESUMEN
La ecuación de flujo permanente gradualmente variado se expresa en función
de la pendiente crítica
Sc . De esta manera, se demuestra que la gradiente de profundidad El Cuadro 3 muestra un resumen de las curvas de remanso. Adicionalmente se provéen calculadores en línea para completar la experiencia [onlinecalc.sdsu.edu].
BIBLIOGRAFÍA Chow, V. T. (1959). Open-channel hydraulics. McGraw-Hill, New York. Henderson, F. M. (1966). Open channel flow. MacMillan, New York. USDA Soil Conservation Service. (1971). Classification system for varied flow in prismatic channels. Technical Release No. 47 (TR-47), Washington, D.C.
1
Estudiante de postgrado en ingeniería civil, Universidad Estatal de San Diego, California, EE.UU.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 130523 15:30 |