| CAPÍTULO 5: FLUJO UNIFORME |
5.1 FLUJO UNIFORME
El flujo uniforme se presenta únicamente en canales prismáticos.
En el flujo uniforme, la profundidad de flujo, el área de flujo, la velocidad media, y la descarga (o caudal) son constantes a lo largo del canal.
El término flujo de equilibrio se utiliza para describir la condición de flujo en canales no prismáticos (naturales) de sección transversal no uniforme, el cual es equivalente al flujo uniforme en canales prismáticos.
En el flujo uniforme, todas las pendientes, la pendiente de fricción Sf, la pendiente de energía Se, la pendiente de la superficie del agua Sw, y la pendiente de fondo So, son constantes e iguales a una pendiente: S.
Sf = Se = Sw = So = S
| (5-1) |
El flujo no permanente no existe; si el flujo es no permanente, entonces no es uniforme.
Sin embargo, para el número de Vedernikov V = 1, el flujo uniforme se convierte en neutralmente estable, lo cual conduce a las ondas de rollo (Sección 1.3).
Esta condición es la "inestabilidad del flujo uniforme" descrita por Chow (1959).
Cuando V < 1, las perturbaciones del flujo se atenúan, y las olas de rodillo no se forman.
Establecimiento del flujo uniforme
Desde un punto de vista mecánico, el flujo uniforme ocurre en un volumen de control cuando la fuerza de fricción es igual a la fuerza gravitacional.
En ausencia de controles de sección (Sección 4.3), todos los flujos en canales tienden a ser uniformes.
En principio, a la naturaleza "le gusta el flujo uniforme."
En el flujo uniforme, la característica única de la curva de gasto (es decir, la singularidad de la relación profundidad-descarga) lo califica como control.
Por lo tanto, el flujo uniforme crítico es un tipo de control muy fuerte.
La profundidad del flujo uniforme se conoce como profundidad normal.
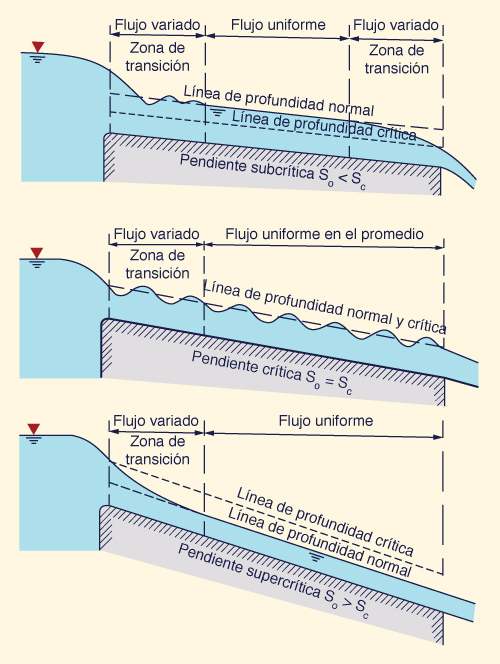
La Figura 5-1 muestra la formación de flujo uniforme en un canal relativamente largo.
La figura superior representa el flujo normal subcrítico, con las secciones de control aguas arriba y aguas abajo.
La figura central representa el flujo crítico, con las secciones de control aguas arriba y aguas abajo.
La figura inferior representa el flujo normal supercrítico, con la sección de control aguas arriba únicamente.
|
Velocidad del flujo uniforme
En general, la velocidad media del flujo uniforme se describe por la siguiente fórmula:
| V = C R x S y | (5-2) |
en la cual C = coeficiente de fricción, R = radio hidráulico, definido como R = A/P, y x e y son los exponentes de R y S, respectivamente.
Los exponentes varían de acuerdo al tipo de rugosidad (laminar, turbulenta, de transición, o mixta laminar-turbulenta) y la forma de la sección transversal (arbitraria, hidráulicamente ancha, rectangular, trapezoidal, triangular, o inherentemente estable).
En la práctica, hay dos fórmulas clásicas para el flujo uniforme:
La fórmula de Chézy, y
La fórmula de Manning.
Actualmente se usan también variaciones de estas fórmulas, como son las fórmulas de Chézy adimensional y Manning-Strickler.
5.2 LA FÓRMULA DE CHÉZY
Para derivar la fórmula de Chézy, el esfuerzo cortante desarrollado a lo largo del fondo del canal se modela con la ley de fricción cuadrática:
| τb = ρ f V 2 | (5-3) |
en la cual ρ = densidad de la masa, f = un tipo de factor de fricción (coeficiente de resistencia), y V = velocidad media.
Esta ecuación es adimensional, por lo tanto, tiene una base teórica.
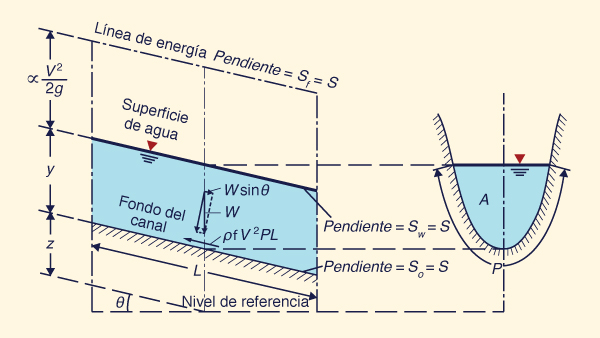
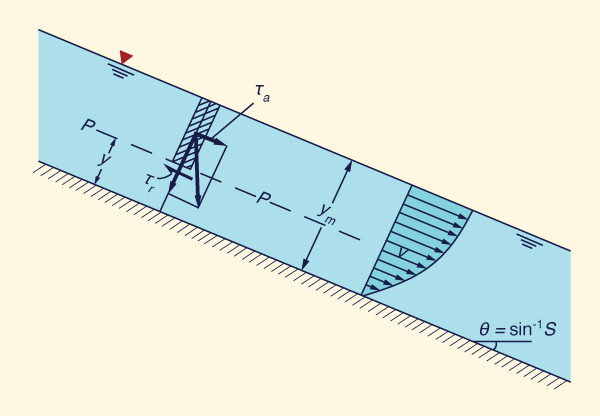
El esfuerzo cortante desarrollado a lo largo del perímetro mojado de un volumen de control de longitud L es (Fig. 5-2):
| Fs = τb PL = ρ f V 2 PL | (5-4) |
|
El peso del agua contenido en el volumen de control es W.
Esta fuerza gravitacional se resuelve a lo largo de la dirección del movimiento de la siguiente manera:
| Fg = W sin θ | (5-5) |
Para un canal de pequeña pendiente: sin θ ≅ tan θ = S. Por lo tanto:
| Fg = W tan θ = W S = γ A L S | (5-6) |
Igualando las fuerzas de fricción (Eq. 5-4) y gravitaional (Eq. 5-6):
| ρ f V 2 P = γ A S | (5-7) |
lo cual se reduce a:
| f V 2 = g (A /P ) S = g R S | (5-8) |
en la que R = radio hidráulico.
Resolviendo para V:
| V = (g/f )1/2 (R S ) 1/2 | (5-9) |
| V = C (R S )1/2 | (5-10) |
en la cual C = coeficiente de Chézy, se define como sigue:
| C = (g/f )1/2 | (5-11) |
Por lo tanto, el factor de fricción f en la Ec. 5-3 es:
| g f = ______ C 2 | (5-12) |
La Ecuación 5-10 es la fórmula de Chézy.
De la Ec. 5-8 se puede derivar una variación de la fórmula de Chézy:
|
V 2 S = f _____ g R | (5-13) |
lo cual equivale a:
|
D V 2 S = f _____ _____ R g D | (5-14) |
Dada la Ec. 4-6, la Ec. 5-14 se reduce a:
|
D S = f _____ F 2 R | (5-15) |
La Ecuación 5-15 es básicamente igual que la Ec. 4-5, la cual se deriva de la ecuación de Darcy-Weisbach aplicada para el flujo en canales abiertos.
Por lo tanto, la ecuación de Chézy adimensional (Ec. 5-15) y la ecuación de Darcy-Weisbach modificada (Ec. 4-5) son esencialmente las mismas.
Para un canal hidráulicamente ancho, D ≅ R, y la Ec. 5-15 se reduce a:
|
S = f F 2 | (5-16) |
lo cual es igual a la Ec. 4-8.
La Tabla 5-1 muestra los valores correspondientes de f, el factor de fricción de Darcy-Weisbach f, y los coeficientes de Chézy.
|
Ver también Video de Laboratorio: Establecimiento del flujo uniforme . |
| ||||||||||||||||||||||||||
| ||||
|
Antoine Chézy nació el 1 de Septiembre de 1718 en Chalon-sur-Marne, Francia, y murió el 4 de Octubre de 1798.
En 1749, trabajando en Amsterdam, Cornelius Velsen declaró:
En 1757, en Hannover, Alemania, Albert Brahms escribió:
"La acción desaceleradora de la fricción de fondo en un flujo uniforme no sólo es igual a la acción aceleradora de la gravedad sino también es proporcional al cuadrado de la velocidad."
Velsen y Brahms estaban trabajando en las leyes generales y teorías de Torricelli y Bernoulli. Chézy usó algunas de estas ideas para desarrollar su fórmula.
A Chézy se le dio la tarea de determinar la sección transversal y la descarga para un canal en el río Yvette, cerca de París, pero a una mayor elevación. Desde 1769, fue recopilando datos experimentales del canal de Courpalet y del río Sena. Sus estudios y conclusiones figuran en un informe al Sr. Perronet con fecha del 21 de octubre de 1775. El documento original, escrito en Francés, se titula "Tesis sobre la velocidad del flujo en un canal," y está firmado por el Sr. Chézy, Inspector General de la Escuela de Puentes y Caminos. El documento se encuentra en el expediente No. 847, manuscrito No. 1915, de la colección que obra en la biblioteca de la escuela.
En 1776, Chézy escribió otro artículo, titulado: "La fórmula para encontrar la velocidad uniforme que el agua tendrá en un canal de pendiente conocida." Este documento, el cual reside en el mismo archivo [No. 847, Ms. No. 1915], contiene la famosa fórmula de Chézy: V = 272 (ah/p)1/2 en la cual h es la pendiente, a es el área, y p es el perímetro mojado. El coeficiente 272 es aplicable al canal de Courpalet en un sistema de unidades antiguo. En el sistema métrico, el valor equivalente es: V = 31 (ah/p)1/2
Para el río Sena, el valor del coeficiente es 44.
Clemens tradujo los dos documentos de Chézy al Inglés. Riche de Prony, uno de los ex-alumnos de Chézy, fue el primero en utilizar su fórmula. Más tarde, en 1801, en Alemania, Eytelwein utilizó las ideas de Chézy y De Prony para popularizar el uso de la fórmula. |
5.3 LA FÓRMULA DE MANNING
|
|
La fórmula de Manning, en unidades SI, es:
| 1 V = ____ R 2/3 S 1/2 n | (5-17) |
en la cual n = coeficiente de fricción de Manning, factor de fricción, o simplemente n de Manning.
En el sistema de unidades acostumbradas en EE.UU. la fórmula de Manning es:
| 1.486 V = ________ R 2/3 S 1/2 n | (5-18) |
La cantidad 1.486 es un factor de conversión que se deriva de la equivalencia:
El factor es requerido para expresar la ecuación original de Manning (Eq. 5-17) en el sistema de unidades acostumbradas en EE.UU.
A fin de comparar con la fórmula de Chézy, la ecuación de Manning se expresa como sigue:
| 1.486 V = ________ R 1/6 R 1/2 S 1/2 n | (5-19) |
La relación entre los coeficientes de Manning y Chézy se encuentra comparando las Ecs. 5-10 y 5-19:
| 1.486 C = ________ R 1/6 n | (5-20) |
La Ecuación 5-20 implica que mientras C varía con el radio hidráulico, el valor de n es constante.
Esto puede ser aproximadamente cierto para los canales prismáticos (artificiales), pero por lo general no lo es para los canales naturales (Barnes, 1967).
En los canales naturales, el valor de n puede variar con el nivel de la superficie del agua y la profundidad del flujo.
Esto es atribuible a:
-
Las variaciones naturales en la rugosidad del canal con el aumento del nivel del agua, incluyendo el efecto de los flujos de desborde (Fig. 2-15), o
-
Los cambios morfológicos en la fricción total de fondo, la cual se compone de fricción de los granos y fricción de forma, a medida que el flujo varía desde un nivel bajo, a través de un nivel intermedio, hasta un nivel alto (Simons y Richardson, 1966).
Fórmulas empíricas para el n de Manning
Se han desarrolado varias correlaciones entre el n de Manning y el tamaño de la partícula (diámetro del grano).
Williamson (1951) ha correlacionado el factor de fricción de Darcy-Weisbach f con la rugosidad relativa, produciendo la siguiente relación (Henderson, 1966):
| ks f = 0.113 ( ____ ) 1/3 R | (5-21) |
en la cual ks = rugosidad de grano, en unidades de longitud, y R = radio hidráulico.
Dado que f = 8 (g /C 2), la Ec. 5-21 se reduce a:
| 8g R C = ( ________ )1/2 ( _____ ) 1/6 0.113 ks | (5-22) |
En unidades acostumbradas en EE.UU., la Ec. 5-22 puede ser reducida a:
|
1.486 R1/6 C = ________________ 0.0311 ks1/6 | (5-23) |
Al comparar la Ec. 5-23 con la Ec. 5-20, se puede expresar n en términos de la rugosidad de fondo de la siguiente manera (ks en pies):
| n = 0.0311 ks1/6 | (5-24) |
En términos de rugosidad relativa y rugosidad absoluta, la expresión general para el n de Manning es (Chow, 1959):
| n = [f (R/ks)] ks1/6 | (5-25) |
lo cual implica que en la Ec. 5-24 la rugosidad relativa es una constante (0.0311).
Suponiendo que la rugosidad límite pueda ser representada por el tamaño d84 de la partícula, es decir, aquél para el cual el 84% de los granos (por peso) son más finos, la Ec. 5-24 se convierte en:
| n = 0.0311 d841/6 | (5-26) |
Strickler utilizó una constante (0.0342) para la rugosidad relativa f(R/ks), y el tamaño medio de la partícula d50 como el diámetro representativo de grano, para producir la ecuación:
| n = 0.0342 d501/6 | (5-27) |
Dado que d84 > d50, se observa que las ecuaciones de Strickler y Williamson son mutuamente consistentes.
La Tabla 5-2 muestra los valores de n de Manning calculados con la fórmula de Strickler (Ec. 5-27).
| ||||||||||||||
| ||||
|
Robert Manning nació en Normandía, Francia, en 1816, y murió en 1897. En 1826, se mudó a Waterford, Irlanda, y trabajó como contador. En 1846, durante el año de la gran carestía, Manning fue reclutado por la División de Drenaje Arterial de la Oficina Irlandesa de Obras Públicas. Después de trabajar como dibujante, fue ascendido a ingeniero asistente. En 1848, llegó a ser ingeniero distrital, cargo que ocupó hasta 1855. Como ingeniero distrital, Manning leyó "Traité d'Hydraulique" de d'Aubisson des Voissons, desarrollando luego un gran interés por la hidráulica. De 1855 a 1869, Manning trabajó para el Marqués de Downshire en la supervisión de la construcción de la Bahía del Puerto de Dundrum, en Irlanda, y el diseño de un sistema de abastecimiento de agua en Belfast. Después de la muerte del marqués en 1869, Manning regresó a la Oficina Irlandesa de Obras Públicas como ingeniero asistente. En 1874 Manning ascendió a ingeniero en jefe, cargo que ocupó hasta su jubilación en 1891. Manning no recibió ningún tipo de educación o capacitación formal en la mecánica de fluidos. Su experiencia en la contabilidad y su naturaleza pragmática influyeron en su trabajo y lo llevaron a simplificar problemas. Manning comparó las siete fórmulas más conocidas de la época: Du Buat (1786), Eytelwein (1814), Weisbach (1845), St. Venant (1851), Neville (1860), Darcy y Bazin (1865), y Ganguillet y Kutter (1869). Calculó la velocidad obtenida con cada fórmula para una pendiente dada, y el radio hidráulico variando entre 0.25 m y 30 m. Para cada condición, Manning encontró el valor medio de las siete velocidades y desarrolló la fórmula de mejor ajuste. La fórmula original fue la siguiente: V = 32 [RS (1 + R1/3)]1/2 la cual más tarde simplificó a: V = C Rx S1/2 En 1885, Manning asignó al exponente x el valor de 2/3 y escribió la fórmula de la siguiente manera: V = C R2/3 S1/2 En una carta a Flamant, Manning declaró: "El recíproco de C corresponde aproximadamente al valor de n, según Ganguillet y Kutter, siendo C y n constantes para el mismo canal." El 4 de Diciembre de 1889, a la edad de 73 años, Manning propuso por primera vez su fórmula a la Institución de Ingenieros Civiles de Irlanda. La fórmula salió a la luz en 1891, en un artículo escrito por él mismo titulado "Sobre el flujo de agua en canales abiertos y tuberías," publicado en las Actas de la Institución de Ingenieros Civiles de Irlanda. A Manning no le gustaba su propia ecuación por dos razones: En primer lugar, en aquellos tiempos resultaba difícil calcular la raíz cúbica de un número y además elevarlo al cuadrado para llegar a la potencia 2/3. En segundo lugar, la ecuación era dimensionalmente incorrecta. Por tales razones, Manning desarrolló la siguiente ecuación, la cual es adimensional: V = C (gS)1/2 [R1/2 + (0.22/m1/2 )(R - 0.15 m)]
en la cual m = "altura de una columna de mercurio que equilibra la atmósfera," y C = un número adimensional "que varía con la naturaleza de la superficie." Sin embargo, en los libros de texto de finales del siglo XIX, la fórmula de Manning fue escrita como sigue:
V = (1/n) R2/3 S1/2
A través de su "Manual de Hidráulica," King (1918) popularizó la fórmula de Manning en la forma como se conoce hoy en día, así como la aceptación de que el coeficiente C de Manning fuera el recíproco de la n de Kutter. En los Estados Unidos, al valor n se le conoce como el factor de fricción de Manning, o simplemente como la n de Manning. En Europa, la K de Strickler es la misma que la C de Manning, es decir, el recíproco de n. Cuando se usa K en lugar de n, la ecuación de Manning se conoce como la ecuación de Manning-Strickler, o simplemente Strickler. |
5.4 LA RUGOSIDAD DE MANNING
|
|
Dada la Ecuación 5-17 (o 5-18), una vez que son conocidas tres variables, la cuarta se puede calcular.
Comúnmente, R y S son conocidas, y n se estima, a partir de lo cual se puede calcular V.
Éste es el método directo, el cual es la forma más común de usar de la ecuación de Manning.
Cuando se requiere mayor precisión, o cuando el varlo de n no puede ser estimado con certeza, se puede calcular n midiendo la velocidad V, el radio hidráulico R, y la pendiente de fondo S.
A este procedimiento se le conoce como el método inverso, o el método de calibración.
En la práctica, la mayoría de las aplicaciones de la fórmula de Manning usan el método directo.
Estimación del n de Manning n
No existe un procedimiento exacto para estimar n de Manning.
A continuación se presentan algunas recomendaciones probadas en la práctica.
Recomendaciones para la estimación del n de Manning
|
Chow (1959) ha presentado una colección ilustrada de veinticuatro (24) canales para los cuales los valores de n han sido establecidos.
El rango de valores documentados por Chow es de n = 0.012 (un canal revestido con placas de concreto), a n = 0.150 (un río natural en suelo de arcilla arenosa, con taludes y fondo irregulares).
Chow documentó valores tan bajos como n = 0.008 (plástico acrílico) y tan altos como n = 0.200 (llanuras de inundación de corrientes naturales, con vegetación densa en el verano) (Tabla 5-4).
Estos valores se aplican al flujo turbulento.
Barnes (1967) ha presentado una colección ilustrada a colores de cincuenta (50) cauces fluviales para los cuales el n de Manning ha sido calculado.
La colección de Barnes se puede ver en línea en Características de Rugosidad de Canales Naturales.
El valor más pequeño de n documentado por Barnes es
El valor más alto es
|
|
Arcement y Schneider (1989) han presentado una colección ilustrada a colores de quince (15) llanuras de inundación en el sureste de los Estados Unidos, para las cuales el valor de n ha sido calculado.
La colección de Arcement y Schneider se puede ver en línea en Los Coeficientes de Rugosidad de Manning para los Canales Naturales y Llanuras de Inundación.
El valor más pequeño de n documentado por Arcement y Schneider
es
El valor más alto es
|
|
Los factores que afectan al n de Manning
En la práctica, el valor de n de Manning varía en forma considerable.
En los cauces naturales puede variar desde aproximadamente 0.020
para algunos ríos muy grandes con fondo liso
La Tabla 5-3 describe los diversos factores que afectan el coeficiente de rugosidad de Manning.
|
|
Cowan (1956) ha desarrollado una metodología racional para la estimación del n de Manning.
La ecuación de Cowan es:
| n = (no + n1 + n2 + n3 + n4 ) m5 | (5-28) |
en la cual:
-
no = valor básico de n para un canal recto, uniforme, y liso
-
n1 = valor adicional para tomar en cuenta irregularidades de la superficie
-
n2 = valor adicional para tomar en cuenta las variaciones en tamaño y forma de la sección transversal
-
n3 = valor adicional para tomar en cuenta las obstrucciones
-
n4 = valor adicional para tomar en cuenta el efecto de la vegetación
-
m5 = factor para tomar en cuenta la sinuosidad del canal (meandros).
La Tabla 5-3 muestra los valores que deben ser usados en la Ec. 5-28.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
La Tabla 5-4 muestra los valores de n de Manning para canales de diversos tipos, documentados por Chow (1959).
Para cada tipo de canal, se muestran los valores mínimos, normales, y máximos de n.
Los valores recomendados para el diseño se indican en negrita.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Haga click -aquí- para mostrar completa la Tabla 5-4. |
5.5 CÁLCULO DEL FLUJO UNIFORME
|
|
La descarga del flujo en canales es (Ec. 5-2):
| Q = V A = C R x S y A | (5-29) |
La Ecuación 5-29 se puede expresar como sigue:
| Q = K S y = K S 1/2 | (5-30) |
en la cual K = conducción, definida así:
| K = C R x A | (5-31) |
O, alternativamente:
| Q K = ______ S 1/2 | (5-32) |
De acuerdo a la ecuación de Chézy:
| K = C A R 1/2 | (5-33) |
De acuerdo a la ecuación de Manning, en unidades SI:
| 1 K = ____ A R 2/3 n | (5-34) |
En el sistema de unidades acostumbradas en EE.UU:
| 1.486 K = ________ A R 2/3 n | (5-35) |
La conducción K contiene información sobre la rugosidad y el tamaño y forma de la sección transversal, y no varía con la pendiente del canal.
Canales de rugosidad compuesta
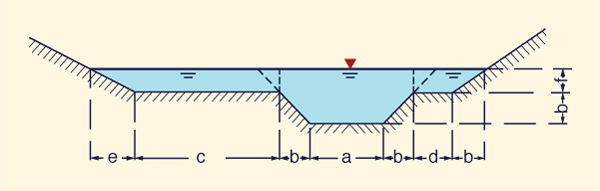
Por lo general, un canal que desborda sus bancos tiene más de un valor de n de Manning: uno dentro del banco, otro fuera del banco izquierdo, y otro fuera del banco derecho (Fig. 5-9).
Se puede calcular un valor compuesto de n bajo el supuesto de que las velocidades en las tres subsecciones son iguales.
Esta suposición es conveniente, pero evade la situación de la posible falta de uniformidad del flujo en una sección transversal compuesta.
Supóngase un canal de rugosidad variable a lo largo de su perímetro mojado, siendo N el número de subsecciones.
Los perímetros húmedos son: P1, P2, P3, ..., PN.
Los valores correspondientes de rugosidad son: n1, n2, n3, ..., nN.
Suponiendo que todas las velocidades son iguales:
|
V1 = V2 = V3 = VN = V | (5-36) |
Para cualquier subsección
| 1 Vi = ____ Ri 2/3 S 1/2 ni | (5-37) |
| 1 Vi = ____ (Ai / Pi ) 2/3 S 1/2 ni | (5-38) |
El área de flujo para la subsección i es:
|
Vi 3/2 ni 3/2 Pi Ai = _________________ S 3/4 | (5-39) |
El área total de flujo es:
|
V 3/2 n 3/2 P A = _________________ S 3/4 | (5-40) |
El área total de flujo es igual a la suma de las subáreas.
Por lo tanto:
| V 3/2 n 3/2 P = ∑ (Vi 3/2 ni 3/2 Pi ) | (5-41) |
| N |
De acuerdo a la Ecuación 5-36, todas las velocidades son iguales.
Por lo tanto, la Ec. 5-41 se reduce a:
| n 3/2 P = ∑ (ni 3/2 Pi ) | (5-42) |
| N |
Por lo tanto, el valor del n de Manning para un canal de sección transversal compuesta es:
| ∑ (ni 3/2 Pi ) N n = [ _________________ ] 2/3 P | (5-43) |
|
La sección transversal de un canal puede estar compuesta de varias subsecciones distintas, cada una con rugosidad diferente.
Por ejemplo, un canal aluvial sujeto a inundaciones estacionales generalmente consiste de un canal principal y dos canales laterales (Fig. 5-9).
Los canales laterales son generalmente más rugosos que el canal principal.
Por lo tanto, la velocidad media en el canal principal es generalmente mayor que las de los canales laterales.
La ecuación de Manning puede aplicarse por separado a cada subsección, y la descarga total es igual a la suma de las descargas de las subsecciones.
Para el canal en su conjunto, la velocidad media es igual a la descarga total dividida entre el área total.
El coeficiente de distribución de velocidades aplicable a todo el canal es diferente de los coeficientes de distribución de velocidades aplicables a cada subsección.
El coeficiente total de distribución de velocidad puede calcularse como se detalla a continuación.
Asumir un número total de subsecciones N y varias subsecciones i, en la cuali varía de 1 a N. De acuerdo a la ecuación de continuidad (Ec. 2-4):
| Qi = Vi Ai | (5-44) |
en la cual Qi = conducción a través de la subsección i, y Vi = velocidad media a través la subsección i, con área de flujo Ai. Además, a partir de la Ec. 5-30:
| Qi = Ki S 1/2 | (5-45) |
en la cual Ki = conducción a través de la subsección i (Ec. 5-33 o 5-34).
Combinando las Ec. 5-44 y 5-45:
| Vi = (Ki / Ai) S 1/2 | (5-46) |
La descarga total es:
| N Q = ∑ Q i i = 1 | (5-47) |
Usando la Ec. 5-45 en la Ec. 5-47:
| N Q = ( Σ Ki ) S 1/2 i = 1 | (5-48) |
De la Ec. 2-4, Q = V A. Por lo tanto:
| N V = ( Σ Ki ) ( S 1/2 / A ) i = 1 | (5-49) |
De la Ec. 2-24, el coeficiente de energía se define como sigue:
|
N Σ Vi 3 Ai i = 1 α = _____________ V 3A | (5-50) |
Asimismo, a partir de la Ec. 2-31, el coeficiente de cantidad de movimiento es:
| N Σ Vi 2 Ai i = 1 β = _____________ V 2A | (5-51) |
Sustituyendo las Ecs. 5-46 y 5-49 en la Ec. 5-50, el coeficiente compuesto de energía α, aplicable a toda la sección transversal es:
N A2 [ Σ (αi Ki 3 / Ai 2 ) ] i = 1 α = ____________________________ N ( Σ Ki ) 3 i = 1 | (5-52) |
Asimismo, sustituyendo las Ecs. 5-46 y 5-49 en la Ec. 5-51, el valor compuesto de β es:
N A [ Σ (βi Ki 2 / Ai ) ] i = 1 β = ____________________________ N ( Σ Ki ) 2 i = 1 | (5-53) |
Cálculo del flujo uniforme
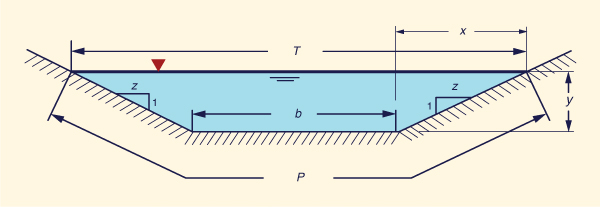
De acuerdo a la Fig. 5-10, se deduce la siguiente proporción: z /1 = x /y.
Por lo tanto, el ancho de superficie T es:
|
T = b + 2x = b + 2zy | (5-54) |
El área de flujo A es:
|
A = (b + x ) y = (b + zy ) y | (5-55) |
|
El perímetro mojado P es:
|
P = b + 2 (y 2 + z 2y 2 )1/2 | (5-56) |
Simplificando:
|
P = b + 2 y ( 1 + z 2 )1/2 | (5-57) |
A partir de la ecuación de Manning, la descarga Q es:
| k Q = _____ A R 2/3 S 1/2 n | (5-58) |
en la cual k = 1 en unidades SI, y k = 1.486 en el sistema acostumbradas en EE.UU.
Dado que R = A /P, la Ec. 5-58 se reduce a:
| Q n A 5/3 _________ = _______ k S 1/2 P 2/3 | (5-59) |
Sustituyendo las Ecs. 5-55 y 5-57 en la Ec. 5-59:
| Q n [ (b + zy ) y ] 5/3 _________ = _____________________________ k S 1/2 [b + 2 y ( 1 + z 2 )1/2] 2/3 | (5-60) |
Simplificando:
| Q n Q n [ (b + zy ) y ] 5/2 - ( ________ ) 3/2 [ 2 y ( 1 + z 2 )1/2 ] - ( ________ ) 3/2 b = 0 k S 1/2 k S 1/2 | (5-61) |
La profundidad normal y se calcula por medio de la Ec. 5-61 con los siguientes datos de entrada:
Descarga Q,
Ancho de fondo b,
Talud z [z: H a 1: V, Fig. 5-10],
Pendiente de fondo S, y (5) n de Manning.
Por lo tanto, con las Ecs. 5-54 y 5-55:
|
A D = ______ T | (5-62) |
|
Q V = ______ A | (5-63) |
La Ecuación 5-61 es la fórmula general para el flujo uniforme o normal, aplicable a los canales prismáticos de sección transversal trapezoidal.
Para un canal rectangular: z = 0.
Asimismo, para un canal triangular de sección simétrica: b = 0.
Para resolver la Ec. 5-61 se expresa:
| Q n Q n f (y) = [ (b + zy ) y ] 5/2 - ( ________ ) 3/2 [ 2 y ( 1 + z 2 )1/2 ] - ( ________ ) 3/2 b k S 1/2 k S 1/2 | (5-64) |
Sustituyendo la variable x = y:
| Q n Q n f (x) = [ (b + zx ) x ] 5/2 - ( ________ ) 3/2 [ 2 x ( 1 + z 2 )1/2 ] - ( ________ ) 3/2 b k S 1/2 k S 1/2 | (5-65) |
La Ecuación 5-65 se resuelve mediante un procedimiento de prueba y error.
A continuación se describe un algoritmo basado en el valor de la función.
La Figura 5-11 es un ejemplo del flujo normal.
Algoritmo para calcular la profundidad normal basado en el
valor de la función
|
|
La aproximación de Newton
El algoritmo anteriormente descrito utiliza únicamente el valor de la función para aproximarse a la raíz.
La aproximación de Newton basada en la tangente converge más rápidamente.
Para que el método de Newton funcione correctamente, es necesario primero acercarse a la raíz usando la iteración basada en el valor de la función.
De lo contrario, es probable que el método de Newton no converja.
Con referencia a la Fig. 5-12, el valor de la tangente en xo es:
|
f(xo) f '(xo) = _________ xo - xr | (5-66) |
en la cual xo = valor de prueba de x, f(xo) = valor de la función en xo, xr = nuevo valor de x, que se aproxima más a la raíz.
|
Resolviendo para xr de la Ec. 5-66:
|
f (xo) xr = xo - ________ f '(xo) | (5-67) |
Como se muestra en la Fig. 5-12, cuando f (xo) aumenta con xo (como es el caso de la Ec. 5-65) al pasar por la raíz, el valor de la función y el valor de la tangente son positivos; por lo tanto, el denominador de la Ec. 5-66 también es positivo, y xr se encuentra a la izquierda de xo.
Con cada iteración subsecuente, la raíz es aproximada en forma de zig-zag, hasta que la tolerancia especificada sea satisfecha.
Se puede mostrar fácilmente que la Ec. 5-67 también se aplica cuando f (xo) disminuye a medida que xo aumenta, como en el caso del flujo crítico, ver la Sección 4.2.
El valor de f '(x) es:
|
Q n f ' (x) = x 5/2 (5/2) (b + zx ) 3/2 z + (b + zx ) 5/2 (5/2) x 3/2 - ( ________ ) 3/2 [ 2 ( 1 + z 2 )1/2 ] k S 1/2 |
| (5-68) |
Simplificando la Ec. 5-68:
|
Q n f ' (x) = 5 z x 5/2 (b + zx ) 3/2 + 5 x 3/2 (b + zx ) 5/2 - ( ________ ) 3/2 ( 1 + z 2 )1/2 k S 1/2 | (5-69) |
El procedimiento para la aproximación de Newton se describe a continuación.
Algoritmo para calcular la profundidad normal: Aproximación de Newton
|
Ejemplo 5-1.
Usando
CANAL EN LÍNEA 01, calcular la profundidad
de flujo crítico para las siguientes condiciones:
ONLINE CALCULATION. Usando
CANAL EN LÍNEA 01,
la profundidad normal es |
Ejemplo 5-2.
Usando CANAL EN
LÍNEA 01, calcular la profundidad de flujo
crítico para las siguientes condiciones:
CÁLCULO EN LÍNEA.
Usando
CANAL EN LÍNEA 01,
la profundidad normal es |
5.6 CÁLCULO DEL CAUDAL DE AVENIDA
|
|
La combinación de velocidades y profundidades altas que predominan durante una inundación aumenta el riesgo de accidentes y lesiones corporales (Fig. 5-13).
Por lo tanto, generalmente no es posible medir la descarga durante una inundación.
Sin embargo, se puede obtener un estimado de la descarga máxima de forma indirecta, por medio del uso de fórmulas de flujo en canales.
Esta es el principio del método de pendiente-área.
|
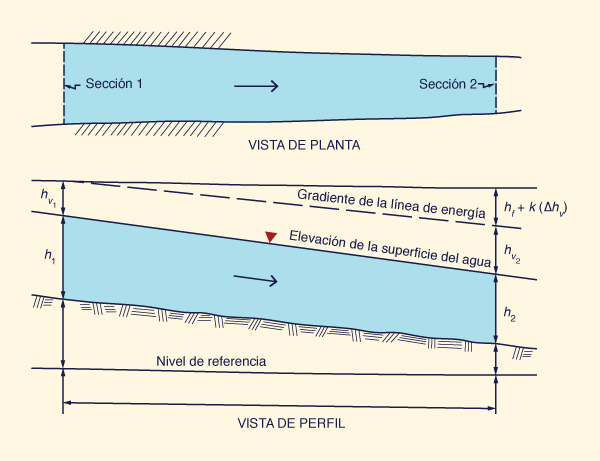
Para aplicar el método de pendiente-área en un tramo de río, se requieren los siguientes datos:
-
La longitud del tramo,
-
La caída, es decir, el cambio de elevación en la superficie del agua a través del tramo,
-
El área de flujo, el perímetro mojado, y los coeficientes de carga de velocidad en las secciones aguas arriba y aguas abajo, y
-
El valor medio del n de Manning para el tramo.
La selección de un tramo adecuado está basada en los siguientes criterios:
-
Las marcas que indican la elevación del agua se deben ser fácilmente identificables(Fig. 5-14).
-
El tramo debe ser lo suficientemente largo para que la caída pueda ser medida con precisión.
-
La forma de la sección transversal y las dimensiones del canal deben ser relativamente constantes.
-
El tramo debe ser relativamente recto, aunque es preferible un tramo con contracción a un tramo con expansión.
-
Se deben evitar puentes, curvas, cascadas y otras características que provoquen una falta de uniformidad del flujo.
|
La precisión del método de pendiente-área mejora a
medida que aumenta la longitud del tramo
Un tramo adecuado debe satisfacer uno o más de los siguientes criterios:
-
La relación de la longitud del tramo a la profundidad hidráulica debe ser mayor que 75,
-
La caída debe ser mayor que o igual a 0.15 m: F ≥ 0.15 m, y
-
La caída debe ser mayor que cualquiera de las cargas de velocidad calculadas en las secciones aguas arriba y aguas abajo.
|
El procedimiento consta de los siguientes pasos:
-
Calcular la conducción K en las secciones aguas arriba y aguas abajo:
1
K1 = ( __ ) A1 R1 2/3
n
(5-70a) 1
K2 = ( __ ) A2 R2 2/3
n
(5-70b) en las cuales K = conducción, A = área de flujo, R = radio hidráulico, n = valor de Manning promedio en el tramo, y 1 y 2 indican los secciones aguas arriba y aguas abajo, respectivamente (La Ec. 5-70 esta dada en unidades SI).
-
Calcular la conducción equivalente del tramo, igual a la media geométrica de las conducciones aguas arriba y aguas abajo:
K = ( K1 K2 )1/2 (5-71) en la cual K = conducción del tramo.
-
Calcular la primera aproximación a la pendiente de energía:
F
S = ___
L
(5-72) en la cual S = primera aproximación a la pendiente de energía, F = caída, y L = longitud del tramo.
-
Calcular la primera aproximación a la descarga pico:
Qi = K S 1/2 (5-73) en la cual Qi = primera aproximación a la descarga pico.
-
Calcular las cargas de velocidad:
α1 ( Qi /A1 ) 2
hv1 = ______________
2g
(5-74a) α2 ( Qi /A2 ) 2
hv2 = ______________
2g
(5-74b) en las cuales hv1 y hv2 = cargas de velocidad en las secciones aguas arriba y aguas abajo respectivamente, α1 y α2 = coeficientes de carga de velocidad aguas arriba y aguas abajo respectivamente, y
g = aceleración de la gravedad. -
Calcular un valor actualizado de la pendiente de energía:
F + k ( hv1 - hv2 )
Si = ___________________
L
(5-75) en la cual Si = valor actualizado de la pendiente de energía, y k = coeficiente de pérdida de carga.
Para el caso de expansión de flujo, es decir,
A2 > A1, k = 0.5; para la contracción de flujo, es decir,A1 > A2, k = 1. -
Calcular un valor actualizado de la descarga pico
Qi = K Si 1/2 (5-76) -
Regresar al paso 5 y repetir los pasos 5 a 7.
El procedimiento termina cuando la diferencia entre dos valores sucesivos de la descarga pico Q obtenida en el paso 7 es despreciable.
En la práctica, generalmente se requieren por lo menos tres iteraciones.
5.7 FLUJO SUPERFICIAL UNIFORME
|
|
El flujo sobre una cuenca o superficie de captación se conoce como flujo superficial.
Generalmente en el flujo superficial, la profundidad de flujo es muy pequeña comparada con el ancho.
Bajo estas condiciones, el flujo puede ser laminar o turbulento, dependiendo de las rugosidades absoluta y relativa.
Si las velocidades y profundidades de flujo son suficientemente pequeñas, el flujo puede ser laminar; de lo contrario, el flujo puede ser transitorio o turbulento, dependiendo del número de Reynolds (Sección 1.4).
En el flujo superficial, suele presentarse un régimen mixto laminar-turbulento.
Este tipo de flujo se caracteriza por cambios de régimen bajo las condiciones de flujo espacialmente variado que normalmente se encuentran en el flujo de superficie.
Cuando el flujo es laminar, el exponente de la curva de gasto es β = 3.
En condiciones de flujo turbulento, el exponente es
Los regímenes mixtos de flujo laminar-turbulento presentan valores de β que varían entre laminar y turbulento.
Flujo superficial laminar
Con referencia a la Fig. 5-16, el esfuerzo de corte que actúa en el nivel P es:
| τa = γ (ym - y ) S | (5-77) |
De acuerdo a la ley de viscosidad de Newton, el esfuerzo de corte en P es proporcional al gradiente vertical de velocidades:
|
dv τr = μ _____ dy | (5-78) |
en la cual μ = una constante de proporcionalidad conocida como viscosidad dinámica.
|
Igualando los esfuerzos actuantes y resistentes:
|
dv μ _____ = γ (ym - y ) S dy | (5-79) |
En forma diferencial:
|
μ dv = γ (ym - y ) S dy | (5-80) |
El peso específico γ = ρg, y la viscosidad dinámica μ = ρν, en la cual ν = viscosidad cinemática.
Por lo tanto, la Ec. 5-80 se reduce a:
| gS dv = _____ (ym - y ) dy ν | (5-81) |
Integrando la Ec. 5-81:
| gS v = ∫ _____ (ym - y ) dy ν | (5-82) |
| gS y 2 v = _____ [ ym y - _____ ] + C ν 2 | (5-83) |
en la cual C es una constante de integración.
Para v = 0, y = 0, por lo tanto: C = 0, y la relación velocidad media/ profundidad de flujo es:
| gS y 2 v = _____ [ ym y - _____ ] ν 2 | (5-84) |
La Ecuación 5-84 indica que el perfil de velocidades en el flujo superficial uniforme tiene una distribución parabólica.
La curva de descarga-profundidad se obtiene integrando la Ec. 5-84 entre los límites de 0 y ym, es decir, desde el fondo hasta la superficie, lo cual resulta en:
| gS y 2 q = ∫ v dy = _____ ∫ [ ym y - _____ ] dy ν 2 | (5-85) |
| gS ym 2 ym 3 q = _____ [ _____ - _____ ] ν 2 6 | (5-86) |
la cual se reduce a:
| gS q = ______ ym 3 3ν | (5-87) |
O a:
|
q = CL ym 3 | (5-88) |
en la cual CL = coeficiente de la curva de gasto correspondiente al flujo laminar, definido como sigue:
| gS CL = ______ 3ν | (5-89) |
En el flujo laminar, el exponente de la curva de gasto es β = 3 (Ec. 5-88), y la curva de gasto es una función de la fricción interna, o viscosidad interna, representada por la viscosidad cinemática ν.
Por lo tanto, el flujo laminar es una función de la temperatura.
Dada la Ec. 5-77, la velocidad media en el flujo laminar, v = q /ym, es:
|
v = CL ym 2 | (5-90) |
La curva de gasto correspondiente al flujo turbulento de acuerdo a Chézy es:
|
q = C S 1/2 ym 3/2 | (5-91) |
La curva de gasto correspondiente al flujo turbulento de acuerdo a Manning, en unidades SI es:
|
q = (1/n) S 1/2 ym 5/3 | (5-92) |
De igual manera, en las unidades acostumbradas en EE.UU.:
|
q = (1.486 / n) S 1/2 ym 5/3 | (5-93) |
Puede observarse que el exponente de la curva de gasto varía
de β = 3 para el flujo laminar
En el flujo superficial uniforme, los valores de β comprendidos en el intervalo entre flujo laminar y turbulento representan la condición mixta laminar-turbulenta (Sección 1.3).
El número de Vedernikov es:
| (β - 1) v V = ____________ (g y )1/2 | (5-94) |
En el caso de V = 1, el flujo es neutralmente estable, lo cual lleva al desarrollo de ondas de rollo (Fig. 5-17).
A continuación se describe la relación entre el exponente β
y el número de Vedernikov
La relación entre el exponente β y el número de Vedernikov
|
|
PREGUNTAS
|
|
¿Cuándo el flujo uniforme se convierte en inestable?
-
¿En qué se basa la fórmula de Chézy?
-
¿Cuál es la diferencia entre las fórmulas de Manning y Chézy?
-
¿Cuál es el valor mínimo del n de Manning que se puede lograr en la práctica?
-
¿Cuál es el rango de valores del n de Manning medido por Barnes?
-
¿Cuál es el rango de valores del n de Manning medido por Arcement y Schneider en llanuras de inundación?
-
¿Por qué el cálculo de rugosidad compuesta utilizando la Ec. 5-43 es sólo una aproximación?
-
¿Cuáles son las cinco variables que se utilizan en el cálculo del flujo uniforme en un canal trapezoidal?
-
¿Por qué es mejor usar la aproximación de Newton en lugar de usar únicamente la aproximación que usa el valor de la función para calcular la profundidad normal?
-
¿Cuál es la relación mínima de la longitud del tramo a la profundidad hidráulica en el método de pendiente-área?
-
¿Cuál es el exponente de la curva de gasto en condiciones de flujo laminar?
-
¿Cuál es el exponente de la curva de gasto en condiciones de flujo turbulento de acuerdo a Chézy en los canales hidráulicamente anchos?
-
¿Cuál es el exponente de la curva de gasto en condiciones de flujo turbulento de acuerdo a Manning en los canales hidráulicamente anchos?
-
¿Bajo qué valor del número de Froude es probable que el flujo llegue a ser inestable en condiciones de flujo laminar?
PROBLEMAS
|
|
-
Demostrar que el factor de fricción de Darcy-Weisbach y la n de Manning se relacionan por medio de la siguiente ecuación:
fD = 8 g n 2 / (k 2 R 1/3)
en la cual el factor de fricción fD = Darcy-Weisbach, g = aceleración de la gravedad, R = radio hidráulico, y k = una constante para el sistema de unidades, igual a 1 en unidades SI y 1.486 en unidades acostumbradas en EE.UU. Expresar la relación en unidades SI y en unidades acostumbradas en EE.UU .
-
Calcular la descarga Q usando la ecuación de Manning, con los siguientes datos: área de flujo A = 23.5 pies2, radio hidráulico R = 5.6 pies, pendiente de fondo S = 0.0025, y n de Manning = 0.035.
-
Calcular la descarga Q usando la ecuación de Manning, con los siguientes datos: área del flujo A = 45 m2; radio hidráulico R = 6 m; pendiente de fondo S = 0.003; n de Manning = 0.04.
-
Dado f = 0.0025, calcular la descarga Q para un área de flujo A = 12.4 m2, radio hidráulico
R = 2.1 m; y pendiente de fondo S = 0.0015. -
Dado f = 0.0035, calcular la descarga Q para un área de flujo A = 18 pies2, radio hidráulico
R = 4.5 pies, y la pendiente de fondo S = 0.0018. -
Usar CANAL EN LÍNEA 01 para calcular la profundidad normal, la velocidad y el número de Froude con los siguientes datos: Q = 150 m3/s, b = 10 m, z = 2, So = 0.0005, n = 0.025.
-
Usar el CANAL EN LÍNEA 01 para calcular la profundidad normal, la velocidad y número de Froude con los siguientes datos: Q = 250 pies cúbicos por segundo, b = 20 pies, z = 1, So = 0.001, n = 0.030.
-
Usando CANAL EN LÍNEA 15, calcular la descarga para un canal prismático, con: b = 20 pies,
y = 3 pies, z = 2, n = 0.025, S = 0.0016.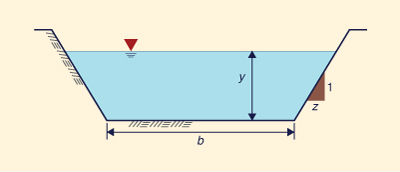
Fig. 5-18 Esquema para un canal trapezoidal.
-
Usando el CANAL EN LÍNEA 15, calcular la descarga para un canal prismático con b = 6 m,
y = 1 m, z = 1.5, n = 0.015, S = 0.0002. -
Una inundación en Clearwater Creek ha dejado marcas de agua observables en un determinado tramo del río. Los datos hidráulicos se han medido en dos secciones transversales A y B, a una distancia de 1,850 pies. La caída del tramo entre las secciones transversales es de 9.1 pies y el n de Manning promedio es 0.035. Aguas arriba, el área de flujo, perímetro mojado, y coeficiente α de Coriolis son 550 pies2, 55 pies, y 1.17, respectivamente. Aguas abajo, el área de flujo, perímetro mojado, y coeficiente α son 620 pies2, 52 pies, y 1.10, respectivamente. Usar PENDIENTE-ÁREA para calcular la descarga de avenida.
-
Calcular la descarga por unidad de ancho en un plano de flujo superficial, bajo flujo laminar y con una profundidad media de 1.5 cm y pendiente de fondo de 0.001. Asumir que la temperatura del agua es T = 20oC. Expresar la descarga en L/s/m.
BIBLIOGRAFÍA
|
|
Arcement, G. J. y V. R. Schneider. 1989. Guide for selecting Manning's roughness coefficients for natural channels and flood plains. U.S. Geological Survey Water-Supply Paper 2339, Washington, D.C.
Barnes, H. A. 1967. Roughness characteristics of natural channels. U.S. Geological Survey Water-Supply Paper 1849, Washington, D.C.
Cowan, W. L. 1956. Estimating hydraulic roughness coefficients. Agricultural Engineering, Vol. 37, No. 7, pp. 473-475, Julio.
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, Nueva York.
Henderson, M. H. 1966. Open-channel flow. Macmillan, Nueva York.
Simons, D. B., y E. V. Richardson. 1966. Resistance to flow in alluvial channels. U.S. Geological Survey Professional Paper 422-J, Washington, D.C.
Williamson, J. 1951. The laws of flow in rough pipes. La Houille Blanche, Vol. 6, No. 5, Septiembre-Octubre, p. 738.
| http://openchannelhydraulics.sdsu.edu |
|
150714 11:00 |