Harley et al. (3) incorporó de manera efectiva el seguimiento de ondas de choque en su modelo de captación basado en el método de características. Trataron las ondas de choque como perturbaciones menores en el campo de flujo regular y simularon características normales y frentes de choque en igualdad de condiciones.

Más recientemente, Borah et al. (1) han presentado una solución analítica a la aproximación de onda cinemática para enrutamiento de flujo no permanente. El modelo permite un flujo de entrada lateral dependiente del tiempo con uniformidad espacial, y está diseñado para su uso en la simulación de flujo de cuencas hidrográficas. Una característica significativa del modelo de Borah et al. es su capacidad explícita para enrutar discontinuidades que puedan desarrollarse durante el curso del cálculo. Una solución basada en el método de las características y un esquema aproximado de amortiguación preserva el efecto del choque y permite el enrutamiento de una variedad de flujos no permanentes, que van desde simples cascadas hasta cuencas naturales complejas.

Otras referencias al cálculo de choques cinemáticos se encuentran dispersas en la literatura. Por ejemplo, Smith (11) desarrolló un método para predecir la tasa de movimiento y atenuación del flujo cinemático sobre un plano permeable. Usando un procedimiento numérico, pudo documentar ciertas características de tipo choque del movimiento de la onda de avenida bajo condiciones iniciales y de contorno específicas. Anteriormente, Tinney y Bassett (12) habían informado sobre trabajos analíticos y experimentales para predecir la forma terminal de un frente de onda poco profundo. Para el caso de flujo turbulento, sus hallazgos confirman la importancia de la longitud del canal de referencia, L_o (Ec. 1), en estudios adimensionales de fenómenos de flujo no permanente en canales.

Aunque el concepto de choque cinemático está bien establecido en el campo del modelado de cuencas hidrográficas, su transposición al enrutamiento de avenidas en corrientes fluviales continua siendo un tema controversial. Algunos investigadores, sobre todo Cunge (2), han llegado a cuestionar por completo su existencia. No hay duda de que la tendencia a empinarse es real. Queda por determinar si las ecuaciones de flujo no permanente gradualmente variado pueden continuar describiendo los fenómenos en las proximidades del choque. Desde un punto de vista práctico, sería interesante determinar las características del flujo y del canal que tenderán a promover o inhibir el desarrollo del choque. En este artículo se sigue esa línea de investigación.

3.  METODOLOGÍA

El enfoque utilizado en este documento para estudiar el potencial de desarrollo de un choque cinemático consiste en lo siguiente: (1) Identificación de los parámetros del flujo y sección transversal del canal; (2) selección del rango de variabilidad de parámetros; (3) selección de un modelo de enrutamiento del flujo; y (4) desarrollo de una estrategia para probar la sensibilidad de los parámetros elegidos al desarrollo de un choque bajo una amplia gama de condiciones.

Identificación de parámetros. En la teoría de flujo no permanente en canales, dos parámetros caracterizan el movimiento de una onda en canales hidraulicamente anchos (6): (1) el número de Froude, F_o = u_o / (g d_o)^1/2; y (2) número de onda adimensional σ = 2π (L_o / L), en las cuales u_o, y d_o = velocidad media y profundidad del flujo, respectivamente; g = aceleración de la gravedad; y L = longitud de onda. El número de Froude contiene información sobre la pendiente del lecho del canal y las características de fricción, mientras que el número de onda adimensional relaciona las escalas de longitud de la onda, L, y la longitud de referencia, L_o. Se necesitan parámetros adicionales en aplicaciones prácticas para tener en cuenta la altura relativa de las ondas y permitir la especificación de cualquier forma de sección transversal. Para tener en cuenta la altura de las ondas (así como la forma general del hidrograma), es necesario seleccionar un tipo de hidrograma de entrada. En este artículo se elige una función gamma como la forma estándar del hidrograma de flujo de entrada. La ecuación para la función gamma tiene la siguiente forma (9):

t                tp - t      Qt  = Qb + (Qp - Qb) ( ____)r exp( ______ )                                      tp              tg - tp

(2)

en las cuales Q_t = flujo de entrada en el momento t; Q_b = flujo base; Q_p = flujo de entrada pico; t_p = tiempo pico del hidrograma de entrada; t_g = tiempo hasta el centro de gravedad del hidrograma de entrada; y r = t_p / (t_g - t_p).

Dado lo anterior, la relación de entrada flujo base a flujo pico, Q_b / Q_p, fue elegido como un indicador de la altura relativa de las ondas, y el tiempo hasta el pico t_p fue elegido para representar la escala de tiempo del hidrograma.

Con respecto a los parámetros de forma de la sección transversal, los elegidos aquí son los que se utilizan normalmente en aplicaciones de enrutamiento de ondas cinemáticas: el coeficiente α y el exponente β en la relación caudal-área de flujo:

Q = α A β

(3)

en la cual Q = caudal; y A = área de flujo.

Rangos de parámetros. El programa de prueba fue diseñado para variar los parámetros elegidos dentro de rangos adecuados. Para tener en cuenta la variación del número de Froude, se estableció una matriz de cinco pendientes del lecho, S_o , y cinco valores de Manning n, dando lugar a un total de 25 canales, cada uno con un conjunto único de S_o y n. Los valores adoptados de S_o son: 0.01, 0.004, 0.001, 0.0004, y 0.0001; los valores de n son: 0.01, 0.02, 0.04, 0.08, y 0.10. Las pendientes suaves con valores altos de Manning n condujeron a flujos de bajo número de Froude, mientras que las pendientes empinadas con valores bajos de Manning n resultaron en flujos de alto número de Froude, inclusive mayores que 1.

En las ondas de avenida no lineales, la inclinación de la curva ascendente tiende a ser contrarrestada por los efectos de difusión provocados por el componente dinámico. Como lo muestran Ponce y Simons (6), el número de onda adimensional, σ, es un indicador del tamaño relativo del componente dinámico. En consecuencia, para garantizar una cantidad suficiente de empinamiento de onda, sin ser efectada por el efecto dinámico, las ondas simuladas se eligieron para permanecer dentro del ámbito de las ondas cinemáticas y difusivas (generalmente, valores bajos de σ). Para este propósito, el tiempo pico t_p, del hidrograma de flujo de entrada, un indicador del tiempo total de la onda, se utilizó para probar la satisfacción del criterio de onda de difusión desarrollado por Ponce et al. (7) y posteriormente modificado (10) para su aplicación a los hidrogramas gamma:

g N = tp So (___ )1/2  ≥ 15                   do

(4)

en las cuales N = número adimensional; g = aceleración gravitacional; y todas las demás variables han sido definidas previamente. Para cada condición de flujo, la satisfacción de la Ec. 4 garantiza que la onda probada es propiamente una onda cinemática/difusiva y, por lo tanto, en gran parte libre de efectos difusivos muy marcados, los cuales tienden a contrarrestar el desarrollo del choque.

Fig. 1  Secciones transversales rectangulares/trapezoidales/triangulares utilizadas en este estudio

El efecto de la altura relativa de las ondas se tuvo en cuenta variando la relación entre el flujo base y el flujo pico. Se eligieron dos relaciones para este estudio: (1) Un valor bajo, Q_b /Q_p = 0.05 (etiquetado L); y (2) un valor alto, Q_b /Q_p = 0.50 (etiquetado H).

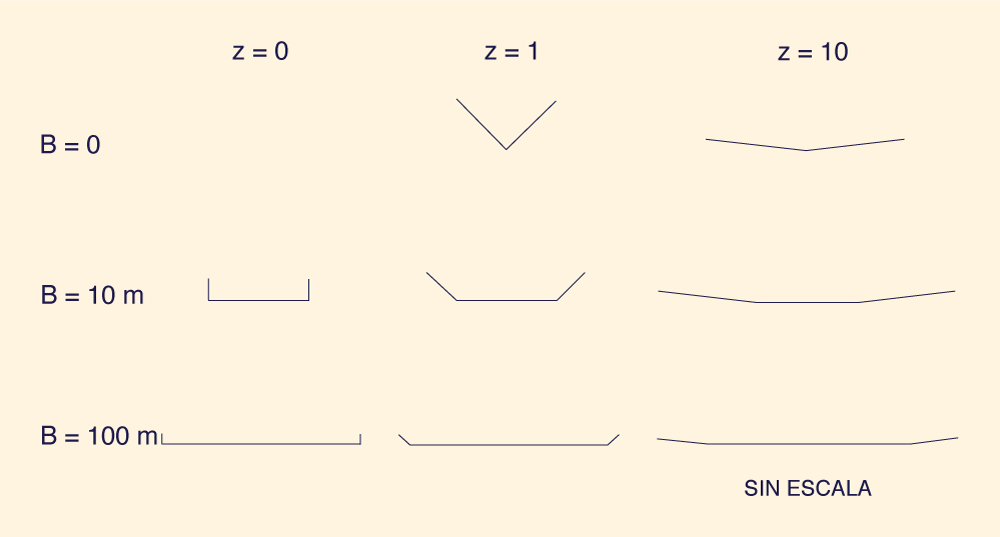
Una cuantificación completa de la variación de los parámetros de forma de la sección transversal, α y β, se consideró demasiado ambiciosa. Se diseñó un programa limitado, pero significativo, mediante la selección de una familia de secciones transversales rectangulares/trapezoidales/triangulares, utilizando tres anchos de fondo y tres pendientes laterales (Fig. 1). Los anchos inferiores elegidos son B = 0, 10, y 100 m; las pendientes laterales son z = 0, 1, y 10 (0 = horizontal: 1 = vertical). Esto conduce a ocho canales (el caso de B = 0 y z = 0 es trivial), lo cual abarca una amplia gama de formas de sección transversal. En general, el valor de β varía del valor teórico (fricción de Manning) β = 1.667 para canales anchos de sección rectangular (B = 100 y z = 0), a β = 1.333 para canales triangulares (B = 0 y z = 1). La excepción es el caso de canales angostos y rectangulares (B = 10, z = 0), asociados con números de Froude bajos (grandes profundidades de flujo), para los cuales el valor de β se aproxima a 1. Se considera que los ocho canales mencionados proporcionan una amplia gama de valores de β para el análisis de sensibilidad.

Selección del modelo. Se seleccionó el modelo SYS75 como modelo numérico para realizar el presente estudio. Este modelo es un programa de computadora desarrollado por el primer autor, el cual presenta un módulo de enrutamiento de coeficientes basado físicamente en el que los parámetros de enrutamiento pueden variar en el tiempo y el espacio (8). Esto le da la capacidad de enrutar ondas de avenida no lineales y, por lo tanto, la capacidad de estudiar el empinamiento de las ondas causada por la no linealidad. El modelo puede calcular el caudal, el área de flujo y el tirante de manera discreta en el espacio y el tiempo, cuando se le presenta las condiciones iniciales y de contorno apropiadas. La precisión del modelo SYS75 ha sido ampliamente documentada (10) y se considera adecuado para el enrutamiento de ondas cinemáticas y difusivas. Los detalles del modelo SYS75 se incluyen en la referencia (10).

Estrategia del estudio. La estrategia general para lograr los objetivos del estudio consiste en los siguientes pasos: (1) establecer una longitud de canal estandarizada, basada en el volumen total de entrada y el área de flujo máximo por encima del flujo base, para permitir el análisis de los choques en niveles comparables de desarrollo; (2) enrutar los hidrogramas desde aguas arriba hasta el extremo aguas abajo del canal, utilizando el modelo SYS75; y (3) comparar la pendiente de la curva ascendente del hidrograma de salida, S_ro, con el de la curva ascendente del hidrograma de entrada, S_ri (La pendiente se toma como un cambio en el caudal por unidad de tiempo, aproximadamente en el punto medio de la curva ascendente). El radio S_ro/S_ri se interpreta como una medida del potencial de desarrollo de la onda de choque.

Además, otras manifestaciones de la presencia del choque, tales como inestabilidades numéricas, se documentan como parte del estudio.

4.  PROGRAMAS DE PRUEBAS

Como parte de este estudio, se seleccionaron siete canales, cada uno con un conjunto único de pendiente de fondo, S_o y n de Manning. Para fines de identificación, se les asignaron nombres alfabéticos de la A a la G, seguidos de una L o una H, que representan una relación de caudal de entrada base-a-pico baja o alta. El canal F se probó en condiciones L y H, y el canal G se probó en tres relaciones diferentes de t_p, para un total de diez series (Tabla 1). Cada serie se probó con ocho formas de sección transversal (Fig. 1), lo que hace un total de 80 simulaciones.

Tabla 1.  Serie de pruebas. Pendiente de fondo, So (1) Coeficiente de fricción de Manning, n (Fpi, número de Froude del caudal máximo de entrada) 0.01 (2) 0.02 (3) 0.04 (4) 0.08 (5) 0.10 (6) 0.01 DH (2.45) AL (0.26) 0.004 FL, FH (0.70, 0.87) 0.001 BH (0.26) 0.0004 GL, GL1, GL2 (0.10) 0.0001 CL (0.34) EH (0.04)

Para cada serie, la longitud total del canal está estandarizada con respecto al volumen de entrada. El volumen del hidrograma de flujo de entrada V_I, por encima del flujo base, se calcula mediante la siguiente fórmula (10):

m! VI = ______ em (Qp - Qb )tp          mm+1

(5)

en la cual m = t_p /(t_g - t_p) es un entero. La longitud del canal L_c, se estima mediante la siguiente fórmula (10):

VI Lc = ______           Apr

(6)

en la cual A_pr = área de flujo correspondiente a Q_pr = Q_s - Q_b. La Ecuación 6 garantiza que la longitud de enrutamiento L_c está relacionada con el volumen del hidrograma de entrada y, por lo tanto, sigue siendo físicamente significativa para los estudios comparativos de choque cinemático.

La Tabla 2 muestra las características del hidrograma de caudal de entrada y del canal para las diez series probadas aquí.

Tabla 2.  Características del hidrograma de entrada y del canal. Canal (1) Qb, caudal base, (m3/s) (2) Qp , caudal pico, (m3/s) (3) tp, tiempo hasta el pico del hidrograma de caudal de entrada, (s) (4) tg, tiempo hasta el centro de gravedad de los hidrogramas de entrada, (s) (5) VI, volumen del hidrograma de entrada por encima del caudal base, (m3/s) (6) Lc, longitud del canal, (m) (7) AL 1.25 25 900 1,200 31,802 1,000 BH 100 200 14,400 21,600 2,660,060 45,000 CL 25 500 172,800 345,600 223,116,572 1,000,000 DH 50 100 3,600 5,400 332,508 45,000 EH 250 500 172,800 259,200 79,801,806 200,000 FL 2.5 50 3,600 5,400 315,882 12,000 FH 50 100 3,600 5,400 332,508 20,000 GL 125 2,500 57,600 86,400 252,705,719 160,000 GL1 125 2,500 115,200 172,800 505,411,438 320,000 GL2 125 2,500 230,400 345,600 1,010,822,876 640,000

5.  RESULTADOS

Los resultados de las ochenta (80) simulaciones se resumen en las Tablas 3 y 4. Para mayor claridad, a continuación se hace referencia a todas las simulaciones por su identificación de fila y columna tal como se muestra en estas tablas. Por ejemplo, la simulación 34 correspondería a la fila 3 (canal con B = 10 y z = 0) y la columna 4 (series EH).

Tabla 3.  Parámetro de la curva de gasto, α y β. Pará- metro (1) Fila (2) B (3) z (4) Columna 0 1 2 3 4 5 6 7 Canal AL (5) BH (6) CL (7) DH (8) EH (9) FL (10) FH (11) GLa (12) α 1 0 1 0.500 0.395 0.500 5.000 0.050 1.581 1.581 0.125 2 0 10 0.291 0.230 0.291 2.913 0.029 0.921 0.921 0.073 3 10 0 0.239 0.564 0.603 2.933 0.236 0.722 0.935 0.529 4 10 1 0.239 0.342 0.398 2.419 0.053 0.725 0.910 0.132 5 10 10 0.231 0.222 0.276 2.365 0.029 0.702 0.815 0.072 6 100 0 0.047 0.039 0.049 0.467 0.008 0.147 0.149 0.020 7 100 1 0.047 0.041 0.051 0.467 0.009 0.147 0.150 0.021 8 100 10 0.049 0.060 0.071 0.488 0.018 0.152 0.167 0.041 β 1 0 1 1.333 1.333 1.333 1.333 1.333 1.333 1.333 1.333 2 0 10 1.333 1.333 1.333 1.333 1.333 1.333 1.333 1.333 3 10 0 1.563 1.247 1.278 1.567 1.025 1.586 1.486 1.040 4 10 1 1.548 1.369 1.385 1.549 1.326 1.570 1.482 1.328 5 10 10 1.397 1.339 1.342 1.392 1.333 1.415 1.361 1.334 6 100 0 1.664 1.648 1.649 1.664 1.562 1.664 1.661 1.571 7 100 1 1.663 1.640 1.643 1.663 1.544 1.663 1.658 1.555 8 100 10 1.640 1.537 1.548 1.641 1.390 1.646 1.618 1.403 a Los canales (GL, GL1, y GL2) tiene el mismo valor de α y β Nota: B = ancho de fondo (m); z = talud (zH:1V)

Tabla 4.  Relaciones de pendiente final y pendiente inicial, Sro / Sri. Fila (1) B (2) z (3) Columna 0 1 2 3 4 5 6 7 8 9 Canal AL (4) BH (5) CL (6) DH (7) EH (8) FL (9) FH (10) GL (11) GL1 (12) GL2 (13) 1 0 1 1.02 0.61 1.18 1.32 0.31 2.73 1.27 0.42 0.73 1.17 2 0 10 1.24 0.72 1.80 1.45 0.25 3.95 1.40 0.52 1.08 1.98 3 10 0 2.15 0.46 0.59 1.45 0.88 4.00 1.40 0.26 0.04 0.05 4 10 1 2.15 0.69 1.71 1.61 0.31 3.75 1.40 0.45 0.77 1.22 5 10 10 1.47 0.76 2.32 1.71 0.25 4.00 1.47 0.52 1.09 1.77 6 100 0 3.96 0.90 2.95 2.24 0.34 4.90 2.00 0.81 1.70 2.92 7 100 1 3.73 0.91 2.76 2.42 0.35 5.00 2.00 0.94 1.85 2.79 8 100 10 3.20 0.91 2.97 2.64 0.26 6.00 2.33 0.67 1.35 2.79 Nota: B = ancho de fondo (m); z = talud (z H : 1 V)

La Tabla 3 muestra los parámetros de la curva de gasto α y β para todas las simulaciones. El valor de α explica en gran medida la pendiente de fondo del canal y la fricción de fondo y, en menor medida, el efecto del perímetro mojado en la forma de la sección transversal. El valor de β tiene en cuenta la forma de la sección transversal y el tipo de fricción de fondo (ya sea Manning o Chézy). Los valores de α varían de α = 0.008 (simulación 64) a α = 5.000 (simulación 13); los valores de β varían de β = 1.025 (simulación 34) a β = 1.664 (simulación 60). La Tabla 3 muestra que β varía generalmente del valor teórico β = 1.333 para canales triangulares (β = 0) con fricción de Manning, a valores cercanos a los teóricos (β = 1.667 para canales rectangulares anchos, B = 100 y z = 0, con la fricción de Manning). Valores de β fuera del rango anterior se calculan para canales estrechos con profundidades de flujo relativamente grandes (flujos de bajos números de Froude); ver, por ejemplo, valores de β para las simulaciones 34 y 37.

La Tabla 4 muestra las relaciones de pendiente final y pendiente inicial S_ro /S_ri para las ochenta (80) simulaciones. Estas son relaciones de pendientes de la curva ascendente de los hidrogramas de flujo de salida y de entrada, respectivamente. Por lo tanto, cuanto mayor sea la relación, más marcada será la tendencia al desarrollo del choque dentro de la longitud estandarizada del canal. Estos resultados conducen a las siguientes conclusiones:

1. Todos los parámetros tienen un efecto marcado sobre el desarrollo del choque. La relación de pendiente, S_ro/S_ri, es directamente proporcional al número de Froude correspondiente al pico de caudal de entrada (fricción del canal y pendiente de fondo), tiempo hasta el pico t_p, (escala de tiempo de la onda), y β valor (forma de la sección transversal y, en menor medida, tipo de fricción del canal); e inversamente proporcional a la relación Q_b/Q_p (altura relativa de la onda).

2. La escala de tiempo (y por lo tanto, la escala de longitud) de la onda está directamente relacionada con el empinamiento de la onda, como lo muestran los resultados de los canales GL, GL1 y GL2. A medida que t_p aumenta de GL a GL1 y GL2, la onda se vuelve más cinemática y, por lo tanto, más propensa al desarrollo del choque (ver, por ejemplo, la columna 9, en comparación con la columna 8). La excepción a este patrón viene dada por los tramos 37-39, lo que confirma el comportamiento extraño de este canal particularmente estrecho con un valor β cercano a 1. Valores de la relación de pendiente menores que 1 (ver columna 7) indican la atenuación de la onda, en vez de su empinamiento, lo que indica la ausencia del choque.

3. El número de Froude tiene un efecto marcado sobre la pendiente de la onda, como se muestra al comparar los resultados de las columnas 5 (canal FL, número de Froude = 0.7) y 9 (canal CL2, número de Froude = 0.1), las cuales tienen la misma relación Q_b/Q_p, (Q_b = 0.05) y aproximadamente el mismo valor de N (Ec. 4). Por ejemplo, la simulación 85 muestra una relación de pendiente de 6.0, en comparación con 2.79 para la simulación 89.

4. La forma de la sección transversal incorporada en el valor de β también tiene una influencia marcada en la pendiente de la onda. Los canales anchos, (filas 6-8) con valores de β que se acercan a 1.667 muestran una tendencia mucho más fuerte al empinamiento que las ondas de lso canales triangulares (filas 1 y 2, β = 1.333) o estrechos (filas 3-5, β generalmente entre 1.333 y 1.667). La excepción está dada por las simulaciones 37-39, las cuales muestran una difusión muy fuerte debido a los bajos valores de β (β = 1.04).

5. La relación de base-caudal pico de entrada, Q_b/Q_p tiene un efecto marcado sobre la pendiente de la onda, mostrado por los resultados de las columnas 5 y 6 de la Tabla 4. La condición de flujo L consistentemente produjo una relación de pendiente mayor que la condición de flujo H (ver, por ejemplo, la simulación 75, que tiene una relación de pendiente igual a 5.0, en comparación con la simulación 76, que muestra una relación de pendiente de 2.0).

Fig. 2   Hidrograma de caudal de salida típico: (a) simulación 45, mostrando un marcado empinamiento e inestabilidad numérica asociada; (b) simulación 69, mostrando un leve empinamiento de ondas; (c) simulación 47, mostrando la difusión en lugar del empinamiento de la onda.

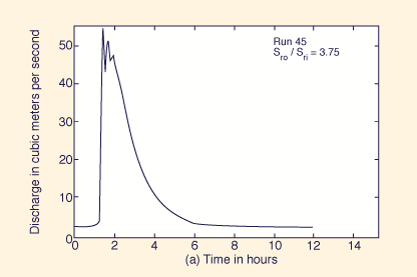
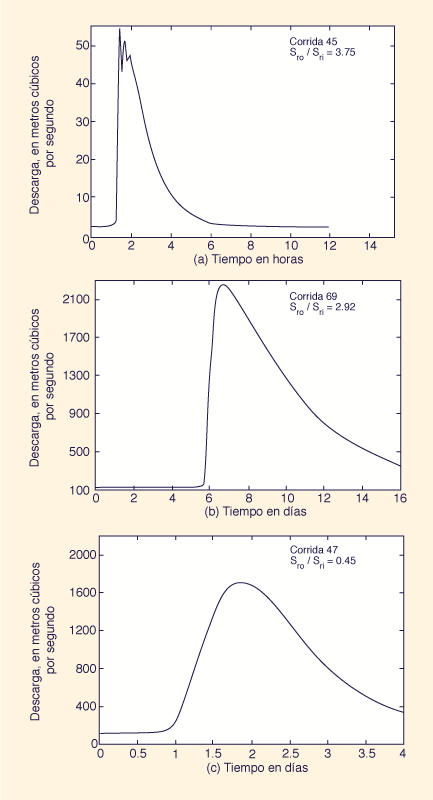
La Figura 2 muestra hidrogramas típicos de caudal de salida: La simulación 45 muestra un pronunciado empinamiento de la onda, y la asociada inestabilidad numérica [Fig. 2(a)]; la simulación 69 es un caso intermedio que muestra un leve empinamiento de la onda [Fig. 2(b)]; y la simulación 47 muestra la difusión en lugar del empinamiento de la onda [Fig. 2(c)].

---

6.  RESUMEN Y CONCLUSIONES

Se ha realizado una serie de experimentos numéricos para determinar el caudal y las características del canal que son más propicias para el empinamiento de la onda cinemática y el fenómeno de choque cinemático asociado. Las características más importantes de flujo y canal se identifican al principio, y se completa un programa de ochenta (80) simulaciones, variando el número de Froude pico del hidrograma de caudal de entrada, el tiempo-al-pico, la relación de caudal base-al-pico y la forma de la sección transversal del canal. Se calculan las longitudes estandarizadas de los canales para permitir el análisis del choque en etapas comparables de desarrollo. Los flujos de entrada del hidrograma gamma se enrutan utilizando un modelo físico de enrutamiento de hidrogramas.

Se encuentra que el número de Froude del pico del hidrograma de entrada, F_pi , tiempo-al-pico, t_p, y relación de caudal base-a-pico, Q_b/Q_p y el parámetro de forma de la sección transversal, β, todos tienen un efecto marcado sobre el desarrollo del choque cinemático. El tamaño de la onda es quizás el principal responsable de la ocurrencia o no ocurrencia del choque. A diferencia de las ondas difusivas, las ondas cinemáticas son más propensas al desarrollo del choque, al igual que las ondas con una relación Q_b/Q_p baja. Los flujos con número de Froude alto son algo más propicios para el desarrollo del choque que los flujos de número de Froude bajo. Los canales rectangulares anchos muestran una tendencia mucho más fuerte al empinamiento que los canales triangulares o angostos. Los valores bajos de β (β próximos a 1.0) aumentan la difusión de la onda e inhiben el desarrollo del choque.

Dados los resultados anteriores, se concluye que es más probable que ocurra un choque cinemático en las siguientes condiciones: (1) Una onda cinemática; (2) una relación baja de caudal base-a-pico; (3) un flujo de alto número de Froude; y (4) un canal ancho y suficientemente largo. Queda por evaluar si se cumplen todas estas condiciones para casos individuales. Por ejemplo, una onda de inundación que se propaga en un canal empinado, inicialmente seco, satisface la mayoría de estas condiciones, por lo que es un caso muy probable para el desarrollo de un choque. Como otro ejemplo, cuando se utiliza un método de enrutamiento de ondas cinemáticas, la primera condición anterior se cumple automáticamente. Por lo tanto, en este caso sólo es necesario satisfacer las otras tres condiciones para el desarrollo del choque.

Los conclusiones anteriores explican la demostrada ausencia del choque cinemático en los cálculos de enrutamiento en llanuras aluviales. A medida que los niveles de agua se elevan por encima del nivel de los bancos, el perímetro mojado aumenta a un ritmo más rápido que para los flujos dentro del banco, lo cual provoca una disminución en el valor de β. Esto contrarresta eficazmente la tendencia al empinamiento y restringe el desarrollo del choque cinemático.

---

APÉNDICE I.  BIBLIOGRAFÍA

1. Borah, D. K., "S". N. Prasad, y C. Alonso. 1980. "Kinematic wave routing incorporating shock fitting," Water Resources Research, Vol. 16, No. 3, June, 529-541.

2. Cunge, J. A. 1969. "On the subject of a flood propagation computation method (Muskingum method)," Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.

3. Harley, B. M., F. E. Perkins, y P. S. Eagleson. 1970. "A modular distributed model of catchment dynamics," Report No. 133, Ralph M. Parsons Laboratory for Water Resources and Hydrodynamics, Massachusetts Institute of Technology, Cambridge, Mass., Dec.

4. Kibler, D.F, y D. A. Woolhiser. "The kinematic cascade as a hydrologic model, "Hydrology Paper No. 39, Colorado State University, Fort Collins, Colo.

5. Lighthill, M. J., G. B. Whitham. 1955. "On kinematic waves. I. Flood movement in long rivers," Proceedings, Royal Society of London, Vol. 4229, May, 281-316.

6. Ponce, V. M., y D. B. Simons. "Shallow wave propagation in open channel flow," Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, Dec., 0977, "pp. 1461-1976".

7. Ponce, V. M., R. M. Li, y D. B. Simons. 1978. "Applicability of kinematic and diffusion models," Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY3, Mar., 353-360.

8. Ponce, V. M., y V. Yevyevich. 1978. "Muskingum-Cunge method with variable parameters," Journal of the Hydraulic Division, ASCE, Vol. 104, No. HY12, Dec., 1663-1667.

9. Ponce, V.M., y F. D. Theurer. 1982. "Accuracy criteria in diffusion routing," Journal of the Hydraulics Division, ASCE, Vol. 108, No. HY6, June, 747-757.

10. Ponce, V. M. 1983. "Accuracy of physically based coefficient methods of flood routing," San Diego State University Civil Engineering Series, No. 83150, Aug.

11. Smith, R.E. "Border irrigation advance and ephemeral flood waves," Journal of the irrigation and Drainage Division, ASCE, Vol. 98, No. IR2, June, 5922, pp. 289-307.

12. Tinney, E.R., y D. L Bassett, "Terminal shape of a shallow liquid Front," Journal of the Hydraulics Division, ASCE, Vol. 87, No. HY5, Sept, 1951, 117-133.

---

APÉNDICE II.  SIMBOLOGÍA

En este artículo se utilizan los siguientes símbolos:

A = área de flujo;

A_pr = área de flujo correspondiente a Q_pr;

B = ancho de fondo;

d_o = profundidad de flujo de referencia;

F = número de Fronde;

F_o = número de Froude del flujo de referencia;

F = número de Froude del flujo pico de entrada;

g = aceleración de la gravedad;

L = longitud de onda;

L_c, = longitud del canal, Ec. 6;

L_o, = longitud de referencia del canal, Ec. 1;

m = t_p / (t_g - t_p), número entero;

N = número adimensional, Ec. 9;

n = coeficiente de fricción de Manning;

P_s = parámetros del choque;

Q = caudal;

Q_b = caudal base;

Q_p = caudal de intrada pico;

Q_pr = Q_p - Q_b;

Q_t = flujo de entrada en el tiempo t;

r = relación t_p /(t_g - t_p );

S_o = pendiente de fondo del canal;

S_ri = pendiente de la curva ascendente del hidrograma de entrada, en unidades L³ / T ²;

S_ro = pendiente de la curva ascendente del hidrograma de salida, en unidades L³ / T ²;

t = tiempo;

t_g = tiempo hasta el centro de gravedad del hidrograma de entrada;

t_p = tiempo hasta el pico del hidrograma de caudal de entrada;

μ_o = velocidad media del flujo de referencia;

V_I = Volumen del hidrograma de entrada por encima del caudal base, Eq. 5;

z = pendiente lateral del canal (z horizontal - 1 vertical);

α = coeficiente en la relación Q-A, Ec. 3;

β = exponente en la relación Q-A, Ec. 3; y

σ = número de onda adimensional, σ = 2π (L_o / L).

---