1. Diffusion Diffusion produces normalcy; lack of diffusion results in chaos. Mother Nature engineered diffusion into every physical process to create stability and make life possible. Diffusion is present in floods. Typical flood waves diffuse, i.e., attenuate or dissipate, albeit ever so slightly most of the time. The essence of flood hydrology is to calculate the amount of diffusion in a flood wave. Thus, flood diffusion is of paramount importance in hydrologic engineering practice. 2. Flood diffusion Flood diffusion exists in all flows with Vedernikov number less than 1 (Ponce 1991). For hydraulically wide channels with Chezy friction, the condition V = 1 is equivalent to Froude number F = 2; for hydraulically wide channels with Manning friction, the condition V = 1 is equivalent to Froude number F = 1.5. Thus, in practice, all [turbulent] flood flows diffuse for Froude numbers F < 1.5. Under natural conditions, it is extremely rare to find flows with Froude numbers greater than 1 (Jarrett 1984). Thus, it may be reasonably argued that given enough time and space, all flood flows will diffuse, i.e., attenuate until they eventually become part of the normal flow (Lighthill and Whitham 1955). Diffusion is a natural law and flood flows follow this natural law. 2. Amount of flood diffusion The amount of flood diffusion is directly controlled by the hydraulic diffusivity of the diffusion wave equation (Ponce 1989). The diffusion wave equation is an extension to the kinematic wave equation to add a diffusion term, i.e., a second-order term. The diffusion coefficient, or kinematic hydraulic diffusivity, originally due to Hayami (1951), is:
in which qo = unit-width discharge, and So = equilibrium channel slope. Ponce (1990) extended the diffusion wave equation into the realm of dynamic waves. Following on the work of Dooge and his collaborators (Dooge et al. 1982), Ponce (1991) expressed the hydraulic diffusivity in terms of the Vedernikov number, effectively creating a dynamic hydraulic diffusivity:
Thus, flood wave diffusion occurs only for Vedernikov numbers V < 1. Note that flood wave diffusion is directly proportional to unit-width discharge and inversely proportional to channel slope. For steep slopes, typically greater than 0.01, diffusion is small and almost negligible; conversely, for mild slopes, typically smaller than 0.0001, diffusion is large. Theoretically, as channel slope approaches zero (0), diffusion approaches infinity (∞). 3. Flood diffusion and drainage area In engineering hydrology, flood wave diffusion increases with drainage area. This observation is supported by Eqs. 1 and 2. The greater the drainage area, the smaller the prevailing overall channel slope and, thus, the greater the wave diffusion. For comparison purposes, Table 1 lists the characteristics of the world's longest/largest rivers, showing mean channel slopes varying between 0.00027 and 0.00087. As expected, local values exhibit a wider range in channel slopes, from greater than 0.10 for certain steep mountain streams (Fig. 2), to around 0.00001 for large rivers in tropical and subtropical regions (Fig. 3).
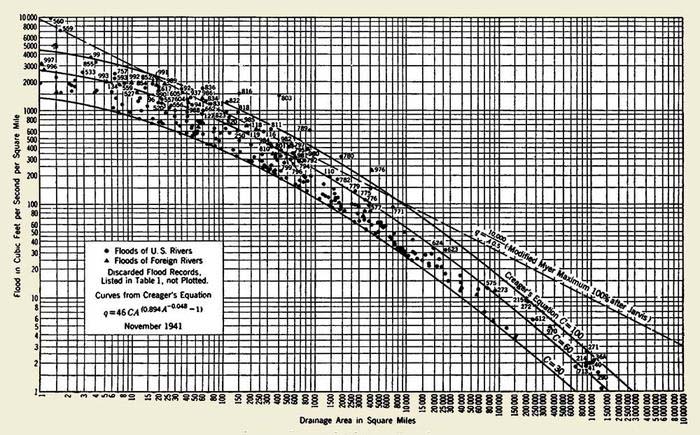
4. The Creager curves An increase in flood wave diffusion with drainage area effectively means that the peak discharge per unit of drainage area will be inversely related to the drainage area. This factual observation was discovered early by Jarvis and Creager, as quoted in Creager et al. (1945). Despite the passage of time, the Creager curves, shown in Fig. 4, remain one of the most comprehensive collections to date of flood peak data vs. drainage area. Diffusion is explicit in the Creager curves; only by diffusion can the reduction of peak discharge [per unit of drainage area] be explained.
According to the Creager formula, the flood peak discharge Q is:
in which C = a coefficient that varies in the range 30 ≤ C ≤ 100. As shown in Fig. 4, the indicated range of C envelopes most of the data compiled by Creager. The C = 100 value includes all maximum, i.e., infrequent floods, while C = 30 value corresponds to the more frequent floods. While Creager did not estimate flood frequency in his formula, the lower value of C may be loosely associated with 2- to 5-yr return periods, while the higher value of C may be tied to the 50- to 100-yr return periods and higher. An online calculator for the Creager formula is given in CREAGER. 4. Summary The Creager curves are reinterpreted and clarified in light of the theory of flood wave diffusion. Experience shows that greater flood wave diffusion corresponds with larger drainage areas. Thus, the trend of the Creager curves admirably reflects the flood wave diffusion that is likely to be present in the real world. Dooge, J. C. I., W. B. Strupczewski, and J. J. Napiorkowski. 1982. Hydrodynamic derivation of storage parameters of the Muskingum model. Journal of Hydrology, 54, 381-387. Hayami, S. 1951. On the propagation of flood waves. Disaster Prevention Research Institute, Kyoto University, Bulletin No. 1, December. Jarrett, R. D. 1984. Hydraulics of high-gradient streams. Journal of Hydraulic Engineering, 110(11), 1519-1539, November. Lighthill, M. J., and G. B. Whitham. 1955. On kinematic waves. I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, Vol. 229, 281-316. Ponce, V. M. 1990. Generalized diffusion wave equation wiuth inertial effects. Water Resources Research, 26(5), 1099-1101, May. Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, 27(7), 1777-1779, July. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 130821 |