En 1975, mientras trabajaba en mi tesis doctoral, me tropecé con el método de estabilidad lineal, por el cual una ecuación diferencial puede ser reemplazada por una ecuación algebraica, y luego ser resuelta para un caso particular. Me di cuenta que este método no había sido aplicado a las ecuaciones de flujo unidimensional no permanente gradualmente variado, las conocidas ecuaciones de Saint Venant. Le pedí permiso a mi profesor consejero para investigar el asunto, dado que el tópico no estaba dentro del tema de mi tesis. Mi consejero preguntó si el problema estaba relacionado con sedimentos, pues nuestro proyecto trataba de hidráulica fluvial. Le dije que este tema no era hidráulica fluvial, sino flujo no permanente en canales. Siguiendo su consejo, dejé el tema a un lado y me apresuré a terminar la tesis, la cual completé en julio de 1976.

Inmediatamente después, fui nombrado profesor asistente de ingeniería civil en mi alma mater, Colorado State University. Vi la oportunidad de descubrir algo de gran importancia, así que estuve los tres meses siguientes, durante tres horas cada noche, aplicando el método de estabilidad lineal a las ecuaciones de Saint Venant. El esfuerzo requirió una habilidad matemática fuera de lo común. Los resultados fueron publicados en diciembre de 1977 en la revista Journal of the Hydraulics Division de la Sociedad Americana de Ingeneros Civiles.¹ Dos años después, en 1979, mi coautor, Dr. Daryl B. Simons y yo recibimos el prestigioso premio Karl Emil Hilgard, de la Sociedad Americana. Este premio se otorga a los autores del mejor artículo publicado en la revista de la División de Hidráulica en el año previo a la competencia.

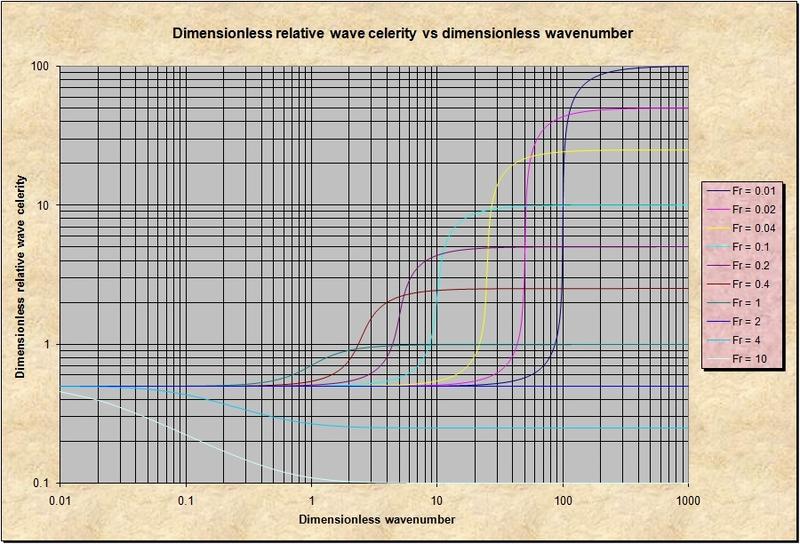
Nuestros resultados se resumen en la famosa serie de curvas S, las cuales muestran la variación de la celeridad relativa adimensional de ondas poco profundas en canales, en función del número de onda adimensional, para un rango apropiado de números de Froude. Las curvas S muestran la progresión, de izquierda a derecha, de ondas cinemáticas (ondas de Seddon) a ondas dinámicas (ondas de Lagrange), a través de una escala espacial adimensional apropiada.

¹ Ponce, V. M., y D. B. Simons. 1977. Shallow wave propagation in open channel flow. ASCE Journal of the Hydraulics Division, Vol. 103, HY12, Diciembre, 1461-1476.