CURVAS DE GASTO REVISADAS
Universidad Estatal de San Diego, San Diego, California
1. INTRODUCCIÓN
Una curva de gasto es una herramienta fundamental en la ingeniería hidráulica e hidrológica. La curva representa la relación entre el caudal y el tirante en un punto determinado de un arroyo, río, canal o conducto de superficie libre. Bajo flujo permanente, la curva de gasto es única, es decir, hay un valor de caudal para cada valor de tirante. Sin embargo, la situación se complica en condiciones de flujo no permanente. Dependiendo del flujo, la clasificación puede no ser única y mostrar una histéresis o una curva de gasto con bucle, es decir, un valor no singular de caudal en función del tirante, y viceversa.
Surgen más complicaciones si el flujo realmente puede mover su lecho, como suele ser el caso en canales y/o ríos aluviales en ausencia de controles geológicos, tales como afloramientos rocosos. En ríos de tamaño mediano a grande, el flujo actúa para minimizar los cambios de nivel de agua, reduciendo efectivamente la variabilidad de cambios entre caudales bajos y altos (Kennedy, 1983). La Naturaleza logra esta hazaña aumentando la fricción de forma durante flujos bajos (mediante el desarrollo de formas de lecho, como ondulaciones y dunas) y borrando estas formas de lecho durante flujos altos, reduciendo así la fricción de forma a cantidades insignificantes, dejando la fricción de grano como la única fricción.
Además, el transporte de sedimentos inestable o en desequilibrio también puede provocar alteraciones o modificaciones en las curvas de gasto previamente establecidas. Los ríos suelen someter sus fronteras a ciclos recurrentes de erosión y deposición, dependiendo de fenómenos naturales vecinos y/o actividades antropogénicas. Algunos ríos activos pueden estar degradando; en cambio, otros pueden estar agradando. Los ríos muy activos pueden cambiar sustancialmente su sección transversal y/o curso/alineación durante inundaciones severas. Invariablemente, los cambios en la curva de gasto son el resultado neto de estos procesos geomórficos.
2. CURVA DE GASTO DE FLUJO UNIFORME PERMANENTE
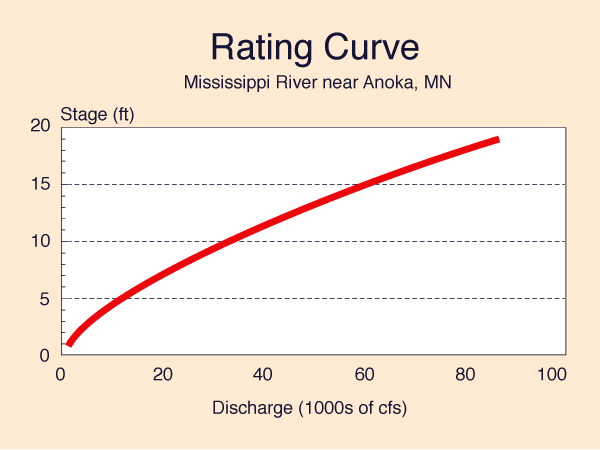
La clasificación de flujo uniforme permanente es una relación única entre el caudal y el tirante en una estación de aforo determinada (Fig. 2). La curva se desarrolla mediante la medición simultánea de caudal y tirante en una estación y ajustando posteriormente la curva a los datos. Para una mayor precisión, la ubicación del sitio de medición debe estar libre de las siguientes condiciones: (1) efectos de remanso, (2) características de flujo inestable (olas) y/o (3) otras irregularidades que tenderían a enmascarar la reproducibilidad de la curva de gasto única.
En la ingeniería práctica, la curva de gasto se utiliza junto con una regla de medición (Fig. 3). Esta última mide la elevación de la superficie del agua, y este valor se ingresa a la curva de gasto para obtener el caudal de interés. Téngase en cuenta que los registradores digitales modernos con capacidades de transferencia electrónica de datos están cada vez más disponibles para la automatización de mediciones.
La permanencia de la curva de gasto normalmente está sujeta a verificación mediante mediciones periódicas de caudal. La frecuencia del proceso de verificación dependerá de si el sitio de interés es óptimo cuando se consideran todos los factores hidráulicos importantes.
3. CURVA DE GASTO EN FLUJO NO PERMANENTE
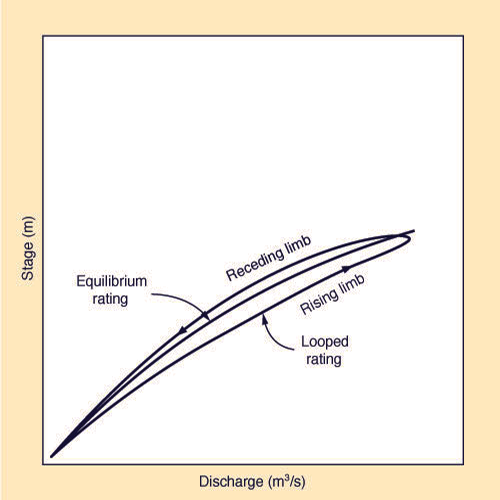
La curva de gasto de un flujo no permanente es un gráfico que muestra una histéresis, mediante la cual la curva de gasto real gira alrededor de la curva de gasto uniforme establecida (Fig. 4). La forma de la curva depende en gran medida del grado de inestabilidad del flujo; cuanto mayor sea la inestabilidad, mayor será el ancho del bucle. El bucle típico es tal que la rama ascendente
4. EFECTOS DE LA SEDIMENTACIÓN A CORTO PLAZO
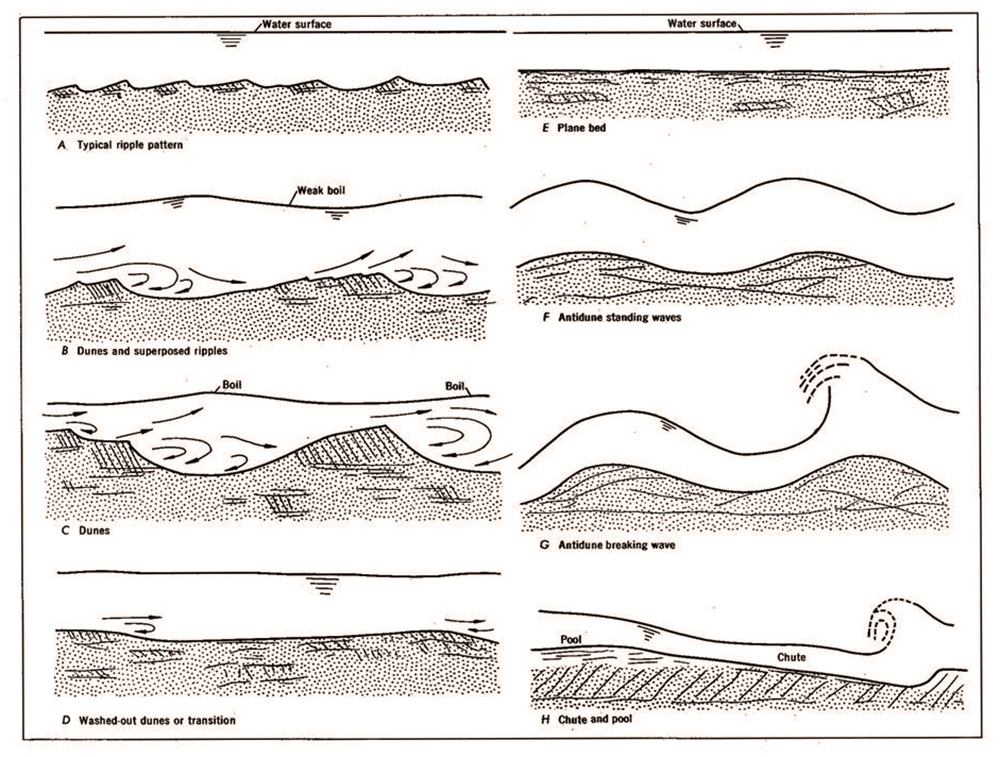
El efecto de sedimentación a corto plazo surge en situaciones donde el esfuerzo cortante de fondo producido por el flujo (debido a la condición de no deslizamiento en la superficie del canal) puede mover su lecho libremente. Éste suele ser el caso de canales/ríos aluviales, en los que el fondo está formado principalmente por partículas de arena y limo. En el régimen inferior, con números de Froude F < 0.5, el esfuerzo de corte de fondo producirá primero ondulaciones y luego dunas, aumentando efectivamente la fricción total, que consiste en fricción de grano y fricción de forma, esta última debida a las formas del lecho. Bajo el régimen superior, los números de Froude F ≥
0.5, el impulso comparativamente grande del flujo actuará para borrar las formas de lecho (ondulaciones y dunas), reduciendo efectivamente la fricción total únicamente a fricción de grano (ver Fig. 5: E Cama plana) (Simons y Richardson, 1966). Así, para caudales bajos, el nivel es más alto de lo normal; por el contrario, para caudales altos, el nivel es más bajo de lo normal. Este fenómeno actúa para reducir la variabilidad entre los tirantes de flujo bajo y alto en corrientes aluviales (Kennedy, 1983). El efecto consiguiente sobre el gasto real puede preveerse fácilmente.
Un ejemplo práctico del efecto de sedimentación a corto plazo lo representa el llamado fenómeno de autodragado, que está bien documentado en el río Alto Paraguay, en Mato Grosso, Brasil (Ponce, 1995). Este fenómeno inusual, que debe interpretarse libremente como el proceso natural de autolimpieza del río, es una autoprofundización del cauce principal del Alto Paraguay hasta una profundidad mínima de 1,2 m (4 pies), excepto en casos aislados en los cuales los afloramientos rocosos no permiten que se realice el autodragado. No debe escapar a nuestra atención que el mantenimiento de una profundidad/nivel de flujo mínimo apreciable mejora tanto la pesca, un componente deseable para la sociedad, como la navegación, una actividad antropogénica.
5. EFECTOS DE LA SEDIMENTACIÓN A LARGO PLAZO
Los ríos tienden a someter sus fronteras a ciclos recurrentes de erosión y deposición, en diversas escalas espaciales. Los mecanismos desencadenantes típicos pueden estar representados por deslizamientos de tierra (Fig. 5) o actividades antropogénicas cercanas (Fig. 6). Normalmente, las estaciones de medición ubicadas adecuadamente no se ven afectadas por los efectos de la sedimentación a largo plazo; sin embargo, esto no se puede garantizar en el futuro. La posibilidad de cambios en la curva de aforos debido a la agradación/degradación a largo plazo o, alternativamente, cambios en el curso del río (Fig. 7) debe ser parte de un programa adecuado de gestión del sitio de medición.
6. CÁLCULO EN LÍNEA
Habiendo explicado con cierto detalle los conceptos básicos de la hidráulica de curvas de aforo, procedemos ahora a calcular esta curva de aforo de una sección transversal de canal trapezoidal. Para lograr este objetivo utilizamos la calculadora online ONLINECHANNEL15B con los siguientes datos de entrada:
Datos de entrada.
Ancho del fondo b = 10 m; profundidad de flujo y = 2 m;
pendiente lateral z = 1; n de Manning n = 0.015; y y pendiente inferior
En la Fig. 8 se muestra un resumen de los resultados de la calculadora en línea.
La ecuación de la curva de aforo es
Q = α A β,
en la cual α = 0.251, y β =
1.585.
7. RESUMEN
Se realiza una revisión de conceptos de curvas de aforo en ingeniería hidráulica e hidrológica.
La curva de aforo del flujo inestable presenta una histéresis o bucle, la cual refleja directamente la cantidad de difusión de onda del flujo inestable (la onda de difusión). El tamaño del bucle está directamente relacionado con la cantidad de difusión.
El efecto de sedimentación a corto plazo se basa en la tendencia de un río aluvial a minimizar los cambios de tirante. Esto se logra modificando la rugosidad del lecho del canal por el propio flujo para aumentar/disminuir la fricción durante flujos bajos/altos. Esta modificación tiene el efecto de reducir la fluctuación del tirante a medida que el flujo cambia de bajo a alto.
El efecto de sedimentación a largo plazo reconoce que los ríos son autores de su propia geometría y que están sometidos recurrentemente a ciclos incesantes de erosión y deposición, tanto de causas naturales como aquéllas inducidas por acciones humanas. Por lo tanto, la cuestión de la permanencia de una curva de aforo debe abordarse teniendo en cuenta posibles cambios geomórficos incidentales.
BIBLIOGRAFÍA
Kennedy, J. F. 1983.
Reflections on rivers, research, y Rouse.
Journal of Hydraulic Engineering ASCE, 109(10), 1257-1260.
Ponce, V. M. y D. B. Simons. 1977.
Shallow wave propagation in open channel flow.
Journal of Hydraulic Engineering ASCE, 103(12), 1461-1476.
Ponce, V. M. 1995. Hydrologic y environmental impact of the Parana-Paraguay Waterway on the Pantanal of Mato
Grosso, Brazil: A reference study. San Diego State University, San Diego, California, August.
Simons, D. B., y E. V. Richardson. 1966.
Resistance to flow in alluvial channels. Geological Survey Professional Paper 422-J,
U.S. Government Printing Office, Washington, D.C.
|
| 240313 |