|
Resumen. Se describe y explica el diseño hidráulico de una transición de canal. El cálculo de una transición de entrada entre un canal y una canaleta se muestra con un ejemplo, presentado originalmente por Hinds (1928) y posteriormente citado por Chow (1959). El ejemplo se reproduce con una explicación detallada y correcciones menores para aumentar la precisión del redondeo. Se proporciona una calculadora en línea.
|
1. INTRODUCCIÓN
Una transición es una estructura del flujo en canales cuyo propósito es cambiar el área de la sección transversal del flujo. El objetivo del diseño es evitar pérdidas excesivas de energía y reducir al mínimo ondas de superficie y otras turbulencias. Cuando la transición está diseñada para mantener las líneas de corriente aproximadamente paralelas, la teoría del flujo gradualmente variado es aplicable. En la práctica, el diseño de transiciones se basa
en el principio de conservación de la energía.
La forma de una transición puede variar desde simples diseños en línea recta hasta complejos diseños en curva. Los diseños en línea recta suelen ser satisfactorios para estructuras pequeñas o cuando existe suficiente carga hidráulica disponible (Fig. 1). Otras simplificaciones son aplicables
siempre y cuando no causen oleaje excesivo o turbulencia (Fig. 2).
Fig. 1 Un ejemplo de transición simple.
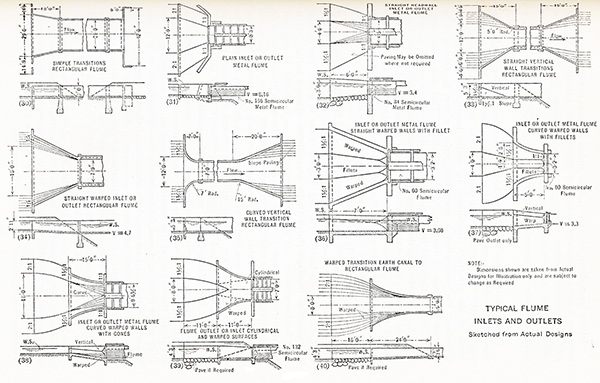
Los tipos más comunes son las transiciones de entrada y salida entre: (1) canal y canaleta, (2) canal y túnel, y (3) canal y sifón invertido. Los cambios bruscos en la profundidad de flujo pueden dar lugar a un flujo rápidamente variado y propiciar la generación de ondas estacionarias.
| [Haga click en la figura para desplegar] |
Fig. 2 Entradas y salidas típicas de canaletas (Hinds, 1928).
2. PROCEDIMENTO DE DISEÑO
Debe prestarse la debida atención a las dimensiones de la transición a lo largo de toda su longitud. El perfil de la superficie del agua debe ser una curva continua, tangente al perfil de la superficie del agua aguas arriba y aguas abajo. En general, deben evitarse
el flujo crítico o salto hidráulico dentro de una transición. Sin embargo, la Seccion 3.6
muestra un ejemplo de una transicion de flujo supercrítico a subcrítico,
con y sin salto hidráulico dentro de la transición.
Se recomienda el uso de una transición con curva en todos los diseños importantes. El procedimiento más apropiado es seleccionar primero la forma de la superficie del agua y luego calcular las dimensiones de las secciones transversales, ajustándose al principio de conservación de la energía.
Transición entre canal y canaleta, o canal y túnel
Las consideraciones de diseño son las siguientes (Hinds, 1928; Chow, 1959):
Longitud y ángulo. Una transición bien diseñada debe seguir las siguientes reglas:
Deben evitarse las esquinas para reducir al mínimo la posibilidad de ondas estacionarias.
El ángulo óptimo subtendido entre el eje del canal y una línea que une los lados del canal entre las secciones de entrada
y salida debe ser aproximadamente 12.5°.
Pérdidas. La pérdida de energía a través de una transición tiene dos componentes:
Pérdida de conversión, la cual se expresa en términos de la diferencia de carga de velocidad entre las secciones de entrada y salida. La Tabla 7-8 muestra los coeficientes de pérdida de conversión.
Pérdida por fricción, la cual se estima con el uso de una fórmula de flujo uniforme.
Esta pérdida es usualmente muy pequeña y puede ser despreciada en un diseño preliminar.
Tabla 7-8 Factores de conversión para evaluar pérdidas de carga
en transiciones.
|
|
Tipo de transición |
Coeficiente de entrada ci |
Coeficiente de salida co |
| Curva |
0.10 |
0.20 |
| Cuadrante cilíndrico |
0.15 |
0.25 |
| Línea recta simplificada |
0.20 |
0.30 |
|
Línea recta |
0.30 |
0.50 |
| Ángulo recto |
≥ 0.30 |
0.75 |
|
Perfil de la superficie del agua. La caída del nivel de la superficie del agua, desde el comienzo de la transición
hasta la mitad, debe ser igual a la mitad de la caída total en toda su longitud. En la primera mitad, las caídas
de cada tramo deben ser proporcionales al cuadrado de la distancia (una parábola hacia adelante). En la segunda mitad,
las caídas deben reflejar aquéllas de la primera mitad, pero en orden inverso (una parábola hacia atrás).
Este procedimiento asegura una curva progresiva para el perfil de la superficie del agua.
-
Bordo Libre. Pueden utilizarse las normas acostumbradas para la estimación de bordo libre en canales revestidos y no revestidos. Cuando la profundidad de flujo excede 12 pies (4 m), el bordo libre debe ser examinado cuidadosamente.
Pérdida de carga en transiciones
En el caso de estructuras de entrada, la velocidad en la sección de entrada es menor que aquélla en la salida. Por lo tanto, la superficie del agua debe caer la diferencia entre las cargas de velocidad, más una pérdida de conversión conocida como la pérdida de entrada. Por lo tanto, la caída Δy' en la elevación de la superficie del agua para la estructura de entrada es:
Δy' = Δhv + ci Δhv = ( 1 + ci ) Δhv
| (7-63) |
en la cual Δhv es la diferencia de carga de velocidad entre las secciones de entrada y salida.
En el caso de estructuras de salida, la velocidad en la sección de entrada es mayor que aquélla en la salida. Por lo tanto, la superficie del agua debe elevarse para recuperar esta diferencia. La subida es igual a la diferencia entre las cargas de velocidad, menos una pérdida de conversión conocida como la pérdida de salida.
Por lo tanto, la subida Δy' en la elevación de la superficie del agua para la estructura de salida es:
Δy' = Δhv - co Δhv = ( 1 - co ) Δhv
| (7-64) |
La Figura 3 muestra los siguientes diseños típicos: (a) una transición de entrada de canal a canaleta, y (b) una transición de salida de canaleta a canal.
La siguiente sección describe en detalle el diseño de una transición de entrada entre canal y canaleta.
|
[Haga click en la figura para desplegar] |
Fig. 3 (a) Diseño de una transición de entrada (Modificado de
Chow, 1959).
|
[Haga click en la figura para desplegar] |
Fig. 3 (b) Diseño de una transición de salida (Chow, 1959).
El diseño de una transición de salida es similar al de una transición de entrada. Sin embargo, a veces la transición de salida se complica debido a la
presencia de una distribución de velocidades no uniforme.
En este caso, es posible que
los coeficientes de distribución de velocidades sean bastante
mayores que uno (1) y, por lo tanto, deben considerarse en el diseño.
Ejemplo del diseño de una transición de entrada
El siguiente ejemplo fue presentado originalmente por Hinds (1928), y posteriormente citado por Chow (1959).
El ejemplo se reproduce aquí con una explicación detallada y correcciones menores de redondeo.
|
Diseñar una transición de entrada para conectar un canal no revestido de ancho de fondo b = 18 pies y talud lateral z = 2 H: 1 V, con un canal rectangular de concreto, de ancho b = 12.5 pies.
Las condiciones hidráulicas son:
Descarga de diseño: Q = 314.5 pies cúbicos por segundo
Pendiente de fondo del canal: S = 0.000246
n de Manning del canal: n = 0.018
Pendiente de fondo de la canaleta: S = 0.0009
n de Manning de la canaleta: n = 0.014
Elevación de la superficie del agua inmediatamente aguas arriba de la transición, en la Estación 0 + 00: Zw,0 = 57.41 pies.
La Tabla 7-9 muestra las propiedades hidráulicas del canal y de la canaleta, correspondiente al flujo normal: profundidad yn (pies),
velocidad Vn (pies por segundo),
área de flujo An (pies cuadrados),
perímetro mojado Pn (pies),
ancho de la superficie, o espejo de agua Tn (pies),
radio hidráulico Rn (pies), y
profundidad hidráulica Dn (pies).
Las propiedades hidráulicas se calcularon utilizando
canalenlinea01.
Tabla 7-9 Propiedades hidráulicas del canal y de la canaleta.
|
| Tipo |
b |
z |
S |
n |
yn |
Vn |
An |
Pn |
Tn |
Rn |
Dn |
| Canal |
18.0 |
2 |
0.000246 |
0.018 |
4.311 |
2.74 |
114.77 |
37.28 |
35.244 |
3.079 |
3.256 |
| Canaleta |
12.5 |
0 |
0.0009 |
0.014 |
4.254 |
5.914 |
53.18 |
21.008 |
12.5 |
2.531 |
4.254 |
|
Solución.
-
Longitud de la transición. Para determinar la longitud de la transición, una línea recta que une la línea de flujo en las paredes en los dos extremos de la transición debe hacer un ángulo θ = 12.5° con la alineación longitudinal. La longitud de la transición es igual a la mitad de la diferencia entre los anchos de superficie en el canal y canaleta, dividido por tan θ:
L =
0.5 ( Tn canal - Tn canaleta ) / tan θ
| (7-65a) |
L =
0.5 (35.244 - 12.5) / 0.2217 = 51.3 pies
| (7-65b) |
Se supone L = 50 pies como un número redondeado a usar para el diseño.
-
Diferencia en la carga de velocidad. La carga de velocidad en la sección transversal inmediatamente aguas arriba de la transición es:
hv = (2.74)2 / (2 × 32.17) = 0.117 pies
| (7-66b) |
De igual manera, la carga de velocidad en la sección transversal inmediatamente aguas abajo de la transición es: hv = 0.544 pies. La diferencia en la carga de velocidad es:
Δhv =
0.544 - 0.117 = 0.427 pies
| (7-67) |
-
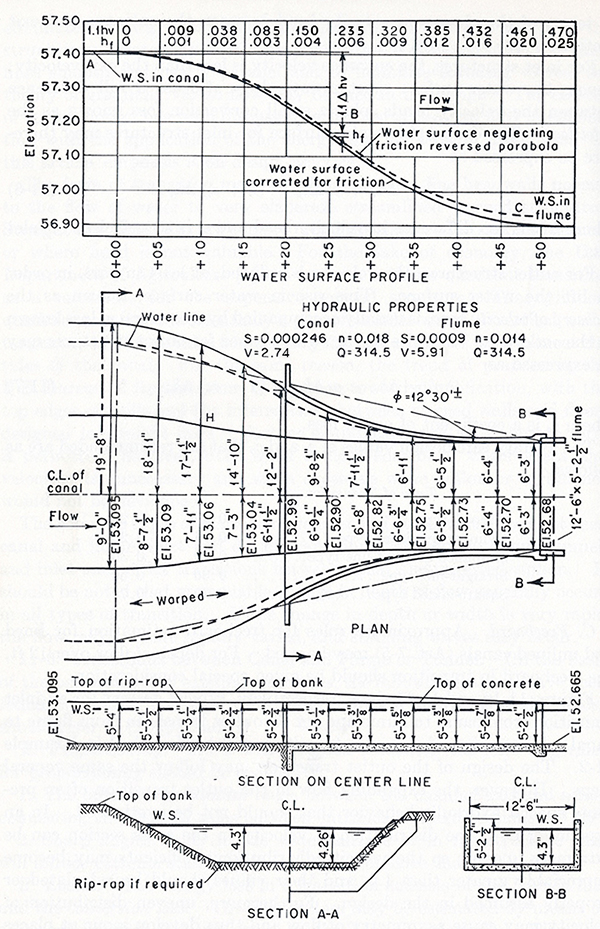
Pérdida de carga, despreciando la fricción. Para la transición en curva mostrada en la Fig. 7-24 (a), el
coeficiente de pérdida de entrada es ci = 0.1 (Tabla 7-8). Por lo tanto, la caída total en el perfil de la superficie del agua, despreciando las pérdidas por fricción, es (Ec. 7-63):
Δy' =
1.1 × 0.427 = 0.470 pies
| (7-68) |
-
Cálculo de la elevación de la superficie del agua. La elevación de la superficie del agua (perfil de la superficie del agua) se
puede aproximar en la forma de dos parábolas tangentes a sí mismas en el punto medio de la transición, y posicionadas de tal manera que la parábola de
aguas arriba es tangente al flujo en el inicio de la transición, y la parábola aguas abajo es tangente al flujo al final de la transición. Las dos
parábolas son tangentes entre sí en el punto medio de la transición (Hinds, 1928). Las siguientes caídas están fijas:
En la sección de aguas arriba, Estación 0 + 00, la caída es Δy'0 = 0.000 pies (inicio);
En el medio de la transición, Estación 0 + 25, la caída es la mitad de la caída total, es decir, Δy'5 = 0.235 pies; y
En la sección de aguas abajo, Estación 0 + 50, la caída es la caída total: Δy'10 = 0.470 pies.
Suponga que la longitud L de la transición se divide en m = 10 subtramos iguales, haciendo un total de once (11) estaciones
o secciones transversales, a una distancia de 5 pies de separación. Para el cálculo de las caídas, se define a
como la mitad de la longitud de la transición; por lo tanto, a = 25 pies. Además, se define b como la
mitad de la caída total en la elevación de la superficie del agua Δy'. Por lo tanto, b = 0.235 pies.
Para cada estación i, la parábola de aguas arriba se define variando i de 1 a 4 como sigue:
Δy'i =
(b /a 2) xi 2
| (7-69a) |
Por ejemplo, para i = 1:
Δy'1 =
(0.235 / 25 2) 5 2 = 0.0094 ≅ 0.009
| (7-69b) |
La parábola de aguas abajo se define variando i de 9 a 6 como sigue:
Δy'i =
Δy'10 -
Δy'10 - i
| (7-69c) |
Por ejemplo, para i = 9:
Δy'9 =
Δy'10 -
Δy'1 = 0.470 - 0.009 = 0.461
| (7-69d) |
Del mismo modo, para i = 8:
Δy'8 =
Δy'10 -
Δy'2 = 0.470 - 0.038 = 0.432
| (7-69e) |
La Tabla 7-10 muestra la caída parcial en la elevación de la superficie del agua Δy'i correspondiente a cada estación i, calculada utilizando la Ec. 7-69. Estos valores se insertan en la Col. 2 de la Tabla 7-11.
Tabla 7-10 Cálculo de la caída en la elevación de la superficie del agua.
|
| Estación |
0+00 |
0+05 |
0+10 |
0+15 |
0+20 |
0+25 |
0+30 |
0+35 |
0+40 |
0+45 |
0+50 |
| i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| xi (pies) |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
| Δy'i (pies) |
0.000 |
0.009 |
0.038 |
0.085 |
0.150 |
0.235 |
0.320 |
0.385 |
0.432 |
0.461 |
0.470 |
|
El procedimiento de cálculo se detalla a continuación, y los resultados se muestran en Tabla 7-11.
-
La Columna 1 muestra las once (11) estaciones, de la Estación 0 + 00 a la Estación 0 + 50.
La Columna 2 muestra las caídas parciales en la elevación de la superficie del agua Δy'.
-
La Columna 3 muestra el cambio en la carga de velocidad Δhv, igual al valor de la Col. 2 dividido por 1.1 (Ec. 7-68).
-
La Columna 4 muestra las cargas de velocidad en cada sección transversal, comenzando con 0.117 pies en el extremo de aguas arriba (Estación 0 + 00), a 0.544 pies en el extremo de aguas abajo (Estación 0 + 50). Para calcular los valores de la Col. 4, para cada estación, se añaden los valores de la Col. 3 al valor de la Col. 4 correspondiente a la Estación 0 + 00 (0.117).
-
La Columna 5 muestra la velocidad V correspondiente a la carga de velocidad hv mostrada en la Col. 4:
V = (2 × 32.17 × hv)1/2
| (7-70b) |
-
La Columna 6 muestra el área de flujo A, la cual se obtiene dividiendo la descarga (Q = 314.5 pies cúbicos por segundo) entre la velocidad correspondiente de la Col. 5.
-
La Columna 7 muestra la mitad del ancho superior 0.5 T, obtenido a partir del plan esbozado [(Fig. 7-24 (a)]. El plan se pueden elegir de manera arbitraria o por tanteos, hasta obtener resultados satisfactorios (Chow, 1959). Los valores mostrados en esta columna son los del ejemplo inicial (Hinds, 1928).
-
La Columna 8 muestra la mitad del ancho inferior 0.5 b, obtenido a partir del plan esbozado [(Fig. 24.7 (a)]. Los valores mostrados en esta columna son los del ejemplo inicial (Hinds, 1928).
-
La Columna 9 muestra la profundidad de flujo y, calculada como sigue:
y = A / (0.5 T + 0.5 b).
| (7-71) |
Cabe indicar que en el extremo de aguas abajo, la profundidad de flujo en la Estación 0 + 50 ha sido ajustada a 4.254 pies.
-
La Columna 10 muestra el perímetro mojado P, calculado como sigue:
P = 2 { 0.5 b + [ ( 0.5 T - 0.5 b )2 + y 2 ] 0.5 }
| (7-72) |
-
La Columna 11 muestra el radio hidráulico R:
-
La Columna 12 muestra la pendiente de fricción Sf, calculada utilizando la ecuación de Manning:
V = ( 1.486 / n ) R 2/3 Sf 1/2
| (7-74) |
Por lo tanto:
Sf = 0.45286 V 2 n 2 R - 4/3
| (7-75) |
en la cual n = 0.014 (el valor de la canaleta) es utilizada para todas las secciones en la transición.
-
La Columna 13 muestra la pérdida de carga por
fricción Δhf entre dos secciones adyacentes,
calculada como la distancia entre éstas
(5 pies) multiplicada por la pendiente de fricción promedio:
Δhf = 5 Sfpromedio
| (7-76) |
-
La Columna 14 muestra la pérdida de carga por fricción, acumulada ∑ Δhf.
|
Tabla 7-11 (a)
Cálculos para el diseño de una transición de entrada.
|
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
(10) |
(11) |
(12) |
(13) |
(14) |
| Variable |
Δy' |
Δhv |
hv |
V |
A |
0.5 T |
0.5 b |
y |
P |
R |
Sf |
Δhf |
∑ Δhf |
| Estación |
(ft) |
(ft) |
(ft) |
(fps) |
(ft2) |
(ft) |
(ft) |
(ft) |
(ft) |
(ft) |
|
(ft) |
(ft) |
| 0 + 00 |
0.000 |
0.000 |
0.117 |
2.740 |
114.771 |
17.600 |
9.000 |
4.315 |
37.243 |
3.082 |
0.000150 |
- |
- |
| 0 + 05 |
0.009 |
0.009 |
0.125 |
2.839 |
110.790 |
17.000 |
8.625 |
4.324 |
36.100 |
3.069 |
0.000160 |
0.000773 |
0.000773 |
| 0 + 10 |
0.038 |
0.034 |
0.151 |
3.116 |
100.947 |
15.427 |
7.917 |
4.324 |
33.166 |
3.044 |
0.000200 |
0.000889 |
0.001662 |
| 0 + 15 |
0.085 |
0.0777 |
0.194 |
3.529 |
89.120 |
13.460 |
7.250 |
4.303 |
29.611 |
3.010 |
0.000250 |
0.001124 |
0.002786 |
| 0 + 20 |
0.150 |
0.137 |
0.253 |
4.037 |
77.900 |
11.228 |
6.958 |
4.284 |
26.013 |
2.995 |
0.000340 |
0.001474 |
0.004260 |
| 0 + 25 |
0.235 |
0.213 |
0.330 |
4.609 |
68.235 |
9.139 |
6.771 |
4.289 |
23.340 |
2.923 |
0.000450 |
0.001966 |
0.006226 |
| 0 + 30 |
0.319 |
0.290 |
0.407 |
5.117 |
61.457 |
7.717 |
6.667 |
4.273 |
22.133 |
2.777 |
0.000600 |
0.002617 |
0.008842 |
| 0 + 35 |
0.385 |
0.350 |
0.467 |
5.480 |
57.387 |
6.847 |
6.563 |
4.279 |
21.704 |
2.644 |
0.000730 |
0.003312 |
0.012154 |
| 0 + 40 |
0.432 |
0.393 |
0.509 |
5.725 |
54.930 |
6.458 |
6.458 |
4.253 |
21.422 |
2.564 |
0.000830 |
0.003895 |
0.016050 |
| 0 + 45 |
0.460 |
0.418 |
0.535 |
5.868 |
53.599 |
6.315 |
6.315 |
4.244 |
21.118 |
2.538 |
0.000880 |
0.004279 |
0.020329 |
| 0 + 50 |
0.470 |
0.427 |
0.544 |
5.914 |
53.177 |
6.250 |
6.250 |
4.254 |
21.008 |
2.531 |
0.000900 |
0.004457 |
0.024786 |
|
-
La Columna 15 [Tabla 7-11 (b)] muestra la elevación de la superficie del agua. En la Estación 0 + 00: Zw,0 = 57.410 pies. Para cada sección transversal i, la elevación de la superficie del agua es:
Zw,i = Zw,0 -
Δy'i - ∑ Δhf,i
| (7-77) |
-
La Columna 16 muestra la elevación del fondo de la transición. Para cada sección transversal i, la elevación del fondo es:
-
La Columna 17 muestra el talud z, calculado como sigue:
z = (0.5 T - 0.5 b) / y
| (7-79) |
-
La Columna 18 muestra la elevación de la parte superior del revestimiento ZL. Para facilitar la construcción del revestimiento, la elevación ZL hace una línea recta a través de la transición. La altura recomendada de revestimiento por encima de la superficie del agua para Q = 314.5 pies cúbicos por segundo es de aproximadamente 1 pie. De acuerdo con esto, el valor de ZL en el punto medio de la transición (Estación 0 + 25) debe ser:
ZL (Estación 0 + 25) = Zw (Estación 0 + 25) + 1
| (7-80a) |
ZL (Estación 0 + 25) = 57.169 + 1 =
58.169
| (7-80b) |
La caída total en la elevación de la superficie del agua a través de la transición es [Tabla 7-11 (b), Col. 15]:
ΔZw = 57.410 - 56.915 = 0.495
| (7-81) |
Para dos secciones transversales adyacentes, la caída en la elevación de la superficie del agua es: 0.495 / 10 = 0.0495. Por lo tanto, la elevación de la parte superior de revestimiento aguas arriba de la transición es:
ZL (Estación 0 + 00) = 58.169 + (5 × 0.0495) = 58.416
| (7-82) |
Del mismo modo, la elevación de la parte superior del revestimiento aguas abajo de la transición es:
ZL (Estación 0 + 50) = 58.169 - (5 × 0.0495) = 57.922
| (7-83) |
Los valores de ZL para las secciones transversales restantes se obtienen por interpolación lineal.
-
La Columna 19 muestra la altura del revestimiento HL, calculada como sigue:
-
La Columna 20 muestra el valor calculado de la mitad del ancho 0.5 W, medido en la parte superior del revestimiento:
0.5 W = z HL + 0.5 b
| (7-85) |
-
La Columna 21 muestra el valor adoptado de la mitad del ancho 0.5 W, medido en la parte superior del revestimiento. Los valores de Col. 21 se indican en la vista en planta mostrada en la Fig. 7-24 (a).
|
Tabla 7-11 (b) Cálculos para el diseño de una transición de entrada (continuación).
|
| (1) |
(15) |
(16) |
(17) |
(18) |
(19) |
(20) |
(21) |
| Variable |
Zw |
Zb |
z |
ZL |
HL |
0.5 W
(calculado) |
0.5 W
(adoptado) |
| Estación |
(ft) |
(ft) |
z H: 1 V |
(ft) |
(ft) |
(ft) |
(ft-in) |
| 0 + 00 |
57.410 |
53.095 |
1.993 ≅ 2 |
58.416 |
5.321 |
19.605 |
19'-8" |
| 0 + 05 |
57.400 |
53.076 |
1.937 |
58.367 |
5.290 |
18.873 |
18'-11" |
| 0 + 10 |
57.371 |
53.046 |
1.737 |
58.317 |
5.271 |
17.071 |
17'-1.5" |
| 0 + 15 |
57.323 |
53.019 |
1.443 |
58.268 |
5.248 |
14.824 |
14'-10" |
| 0 + 20 |
57.255 |
52.972 |
0.997 |
58.218 |
5.246 |
12.188 |
12'-2" |
| 0 + 25 |
57.169 |
52.880 |
0.552 |
58.169 |
5.289 |
9.691 |
9'-8.5" |
| 0 + 30 |
57.082 |
52.809 |
0.246 |
58.120 |
5.310 |
7.972 |
7'-11.5" |
| 0 + 35 |
57.013 |
52.733 |
0.066 |
58.070 |
5.337 |
6.917 |
6'-11" |
| 0 + 40 |
56.962 |
52.709 |
0 |
58.021 |
5.312 |
6.458 |
6'-5.5" |
| 0 + 45 |
56.929/td>
| 52.686 |
0 |
57.971 |
5.286 |
6.315 |
6'-4" |
| 0 + 50 |
56.916 |
52.661 |
0 |
57.922 |
5.260 |
6.250 |
6'-3" |
|
El diseño de una transición puede ser efectuada con la ayuda de la calculadora en línea
onlinetransitiondesign.php
contenido en onlinecalc.sdsu.edu.
3. RESUMEN
Se describe y explica el diseño hidráulico de una transición de canal.
El cálculo de una transición de entrada entre un canal y una canaleta
se muestra mediante un ejemplo, presentado originalmente por Hinds
(1928) y posteriormente citado por Chow (1959). El ejemplo
se reproduce con una explicación detallada y correcciones menores
para aumentar la precisión del redondeo. Se proporciona una calculadora en línea.
BIBLIOGRAFÍA
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, New York.
Hinds, J. 1928. The hydraulic design of flume and siphon transitions. Transactions,
American Society of Civil Engineers, Vol. 92, 14-23-1459.
|