Distribución espacial del flujo permanente alrededor del desplazamiento por gravedad de una partícula esférica dentro de un matraz lleno de agua, Dr. Victor M. Ponce y Jhonath W. Mejía, 2021.

Distribución espacial del flujo permanente
alrededor del desplazamiento por gravedad
de una partícula esférica dentro de
un matraz lleno de agua

Víctor M. Ponce y Jhonath W. Mejía

210308

RESUMEN

El presente artículo tiene por objeto responder la pregunta hecha por el profesor Daryl B. Simons en la Universidad Estatal de Colorado, Fort Collins, a mediados de la década de los años 1970. El problema consiste en determinar la distribución espacial del flujo permanente alrededor de una partícula esférica que cae dentro de un matraz lleno de agua. Para obtener la respuesta a esta pregunta, dados los diámetros de la partícula y el matraz, se parte de la ley fundamental de la conservación de la masa, usando integrales de volúmen y el teorema del valor medio.

1. INTRODUCCIÓN

El presente artículo tiene por objeto responder la pregunta hecha por el profesor Daryl B. Simons en la Universidad Estatal de Colorado, Fort Collins, a mediados de la década de los años 1970. El problema consiste en determinar la distribución espacial del flujo permanente alrededor de una partícula esférica que cae dentro de un matraz lleno de agua. Dados los diámetros de la partícula y el matraz, se parte de la ley fundamental de la conservación de la masa, usando integrales de volúmen y el teorema del valor medio.

2. VELOCIDAD DE CAÍDA

La velocidad de caída de una partícula de sedimento es su tasa terminal de sedimentación en agua estática. La velocidad de caída es función del tamaño, la forma y el peso específico de la partícula, y del peso específico y la viscosidad del agua. Para partículas pequeñas, su forma se puede aproximar al de una esfera; entonces, la velocidad de caída se expresa de la siguiente manera (Ponce, 1989):

             4      g d     γ_s  -  γ
w  =  [ ^___  ^______  ^________ ]^1/2
             3      C_{_D}          γ

(1)

en la cual w = velocidad de caída; g = aceleración de la gravedad; d = diámetro de la partícula; γ = peso específico del agua; γ_{_s} = peso específico de las partículas de sedimentos, y C_{_D} = es el coeficiente de resistencia (al rozamiento). Esta ecuación se puede resolver en forma iterativa con el procedimiento utilizado por enlineavelocidadcaida.

3. DISTRIBUCIÓN DE VELOCIDADES

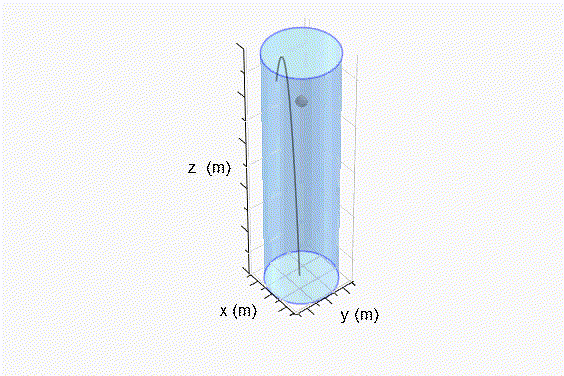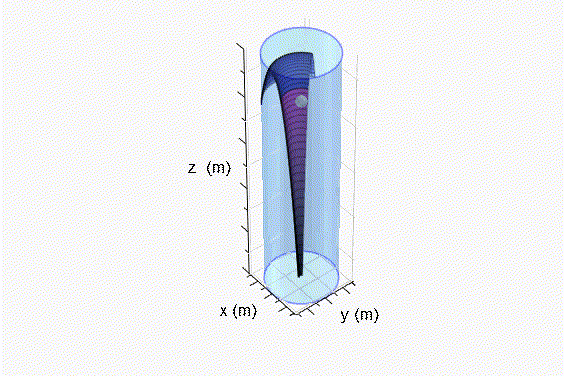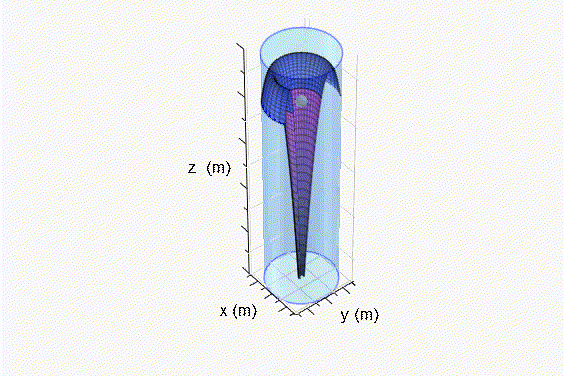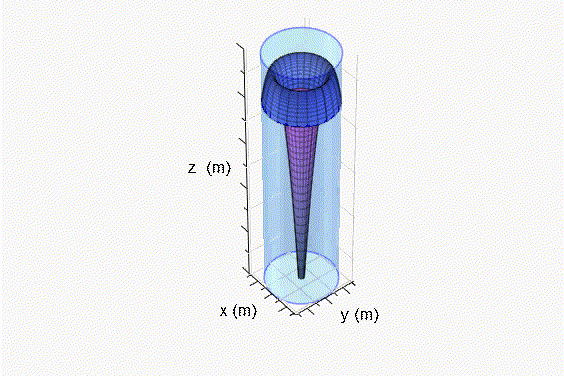
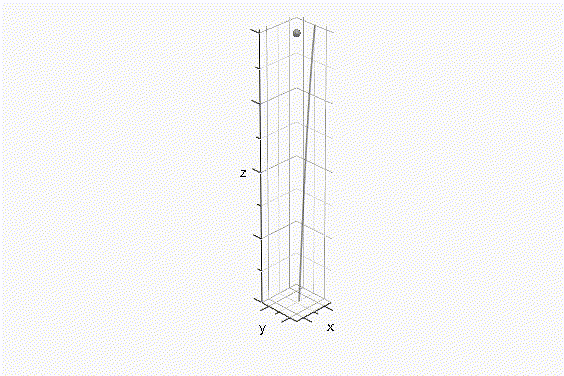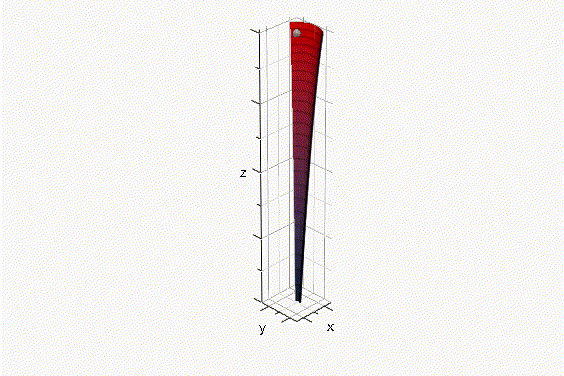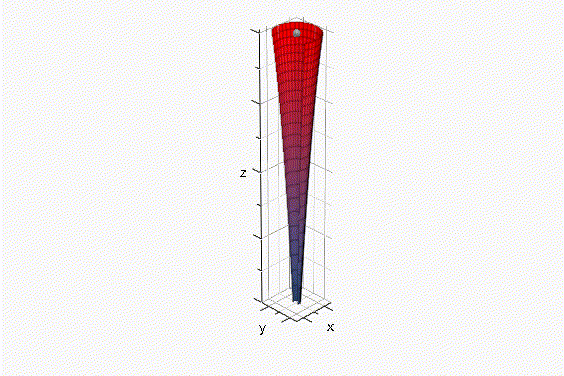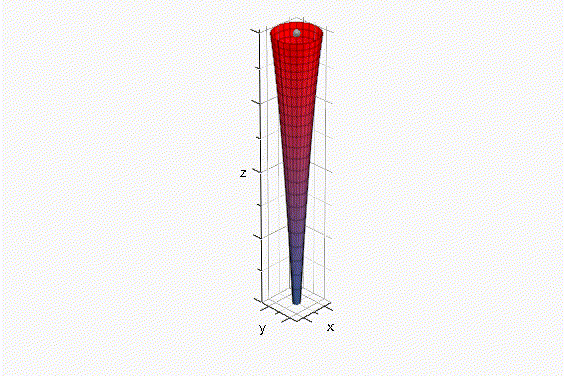
La distribución de velocidades en el espacio entre la partícula y la pared interior del matraz tiene las siguientes características (Fig. 1):

El origen de coordenadas es el centro de la partícula.
El flujo próximo a la partícula está dado por Q_₁, mientras que el flujo próximo a la pared interior del matraz está dado por Q_₂; estos flujos son iguales debido a la ley de la conservación de la masa.
El valor V_₁ es la velocidad de caída de la partícula.
El valor V_₂ es la velocidad máxima del flujo ascendente.
La condición de frontera en la pared interior del matraz es la condición de no deslizamiento, es decir V_{_o} = 0.
El valor c es el punto de intersección entre la distribución de velocidades con el eje de las abscisas, y es donde se establece el equilibrio de los dos flujos Q_₁ y Q_₂.

Fig. 1 Distribución de velocidades en el espacio entre la partícula y la pared interior del matraz.

De la Figura 1 se pueden establecer las siguientes relaciones. La ecuación canónica de una parábola con vértice en (k,V_₂) se define como sigue:

(y - V_₂) = 4P (x - k)^²

(2)

De la Ecuación 2, resolviendo para x, se obtiene:

( y - V_₂)
x_₁ = k + [ ^________ ]^{^1/2}
4P

(3)

(y - V_₂)
x_₂ = k - [ ^________ ]^{^1/2}
4P

(4)

Evaluando la Ec. 2 en p1:(0.5d, -V_₁) y resolviendo para 4P :

- (V_₁ + V_₂)
4P = ^____________
(0.5d - k)^²

(5)

Evaluando la Ec. 2 en p2:(c, 0) y resolviendo para c :

-V_₂
c = k - [ ^____ ]^{^1/2}
4P

(6)

Evaluando la Ec. 2 en p3:(0.5D, 0) y resolviendo para 4P :

-V_₂
4P = ^___________
(0.5D - k)^²

(7)

Igualando las Ecs. 5 y 7:

- (V_₁ + V_₂) - V_₂
^____________ = ^____________
(0.5d - k)^² (0.5D - k)^²

(8)

(V_₁ + V_₂) (0.5d - k)^²
^__________ = ^___________
V_₂ (0.5D - k)^²

(9)

De la Ec. 9, resolviendo para V_₁:

(0.5d - k)^²
V_₁ = V_₂ [ ^___________ - 1 ]
(0.5D - k)^²

(10)

Para R_{_v} = (V_₁ + V_₂) /V_₂ y R_{_D} = (0.5d - k)^²/(0.5D - k)^², las Ecs. 9 y 10 quedan redefinidas como sigue:

R_{_v} = R_{_D}

(11)

V_₁ = V_₂ ( R_{_D} - 1 )

(12)

Sustituyendo la Ec. 7 en las Ecs. 3 y 4, y simplificando:

y
x_₁ = k + (0.5D - k) [ 1 - ^____ ]^{^1/2}
V_₂

(13)

y
x_₂ = k - (0.5D - k) [ 1 - ^____ ]^{^1/2}
V_₂

(14)

4. CONSERVACIÓN DE LA MASA

Al aplicar el principio de conservación de la masa en la Fig. 1, se establece lo siguiente:

Q_₁ - Q_₂ = 0

(15)

Reescribiendo la Ec. 15 en términos de área y velocidad media:

V_{_m1} A_₁ = V_{_m2} A_₂

(16)

en la cual A_₁ = π [c^² - (0.5d)^²] /4, área de flujo del anillo interior; y A_₂ = π [(0.5D)^² - c^²] /4, área de flujo del anillo exterior. A partir de la Fig. 1 y el teorema del valor medio para integrales de volumen definimos la velocidad media V_{_m1} como sigue:

             ∀_{_v1}
V_{_m1}  =  ^_____
              A_₁

(17)

en la cual ∀_{_v1} = Volumen 1. La velocidad media V_{_m2} queda definida como sigue:

             ∀_{_v2}
V_{_m2}  =  ^_____
              A_₂

(18)

en la cual ∀_{_v2} = Volumen 2. Reemplazando las Ecs. 17 y 18 en la Ec. 16:

∀_{_v1}                ∀_{_v2}
^_____  A_₁  =  ^_____  A_₂
  A_₁                 A_₂

(19)

y simplificando se obtiene:

∀_{_v1} = ∀_{_v2}

(20)

La Ecuación 20 representa la condición de equilibrio que existe entre los caudales Q_₁ y Q_₂ según la definición de la Ec. 15 en términos de volúmenes.

Resolviendo ∀_{_v1} usando la integral del volúmen de un sólido de revolución generado por la curva x_₂, dada la Ec. 14:

                _₀                                            y
∀_{_v1}  =  π  ∫ { [ k  -  (0.5D - k) ( 1  -  ^____ )^{^1/2} ]^²  -  (0.5D)^² } dy
                  ^{^-V_₁}                                           V_₂

(21)

                            (0.5D - k)^²           y                      4k (0.5D - k) V_₂       y                                       _₀
∀_{_v1}  =  π [ k^²y  -  ^_________ V_₂ ( ^____  -  1 )^²  +  ^{_______________} ( ^____  -  1 )^{^3/2}  -  (0.5D)^²y ]
                                   2                   V_₂                                3                  V_₂                                     ^{^-V_₁}

(22)

Tomando θ_₁ = (0.5D - k) y θ_₂ = (0.5D), y reemplazando en la Ec. 22:

                            (θ_₁)^²             y                       4k (θ_₁) V_₂         y                                    _₀
∀_{_v1}  =  π [ k^²y  -  ^_____ V_₂ ( ^____  -  1 )^²  +  ^___________ ( ^____  -  1 )^{^3/2}  -  (θ_₂)^²y ]
                               2               V_₂                              3              V_₂                                  ^{^-V_₁}

(23)

Reemplazando los límites (0, -V_₁) para y en la Ec. 23, y simplificando se obtiene:

                  -θ_₁^²V_₂        4k θ_₁V_₂                     θ_₁^²V_₂       V_₁ + V_₂             4k θ_₁V_₂       V_₁ + V_₂
∀_{_v1}  =  π [ ^_______  +  ^________  +  V_₁k^²  +  ^______ ( ^________ )^²  -  ^________ ( ^________ )^{^3/2}  +  (θ_₂)^²V_₁ ]
                      2                 3                             2              V_₂                       3              V_₂

(24)

Tomando R_{_v} = (V_₁ + V_₂) /V_₂ y reemplazando en la Ec. 24:

                  -θ_₁^²V_₂         4k θ_₁V_₂                      θ_₁^²V_₂             4k θ_₁V_₂
∀_{_v1}  =  π [ ^_______  +  ^________  +  V_₁k^²  +  ^______ R_{_v}^²  -  ^________ R_{_v}^{^3/2}  +  (θ_₂)^²V_₁ ]
                      2                 3                               2                     3

(25)

Simplificando:

                  -θ_₁^²V_₂                              4k θ_₁V_₂
∀_{_v1}  =  π [ ^_______ ( 1  -  R_{_v}^² )  +  ^__________ ( 1  -  R_{_v}^{^3/2} )  +  V_₁ (k^²  +  θ_₂^² ) ]
                      2                                      3

(26)

Reemplazando las Ecs. 11 y 12 en la Ec. 26:

                  -θ_₁^²V_₂                               4k θ_₁V_₂
∀_{_v1}  =  π [ ^_________ ( 1  -  R_{_D}^² )  +  ^_________ ( 1  -  R_{_D}^{^3/2} )  +  V_₂ ( R_{_D} - 1 ) (k^²  +  θ_₂^² ) ]
                       2                                        3

(27)

                       -θ_₁^²                            4k θ_₁
∀_{_v1}  =  π V_₂ [ ^_____ ( 1  -  R_{_D}^² )  +  ^______ ( 1  -  R_{_D}^{^3/2} )  -  ( 1 - R_{_D} ) (k^²  +  θ_₂^² ) ]
                         2                                 3

(28)

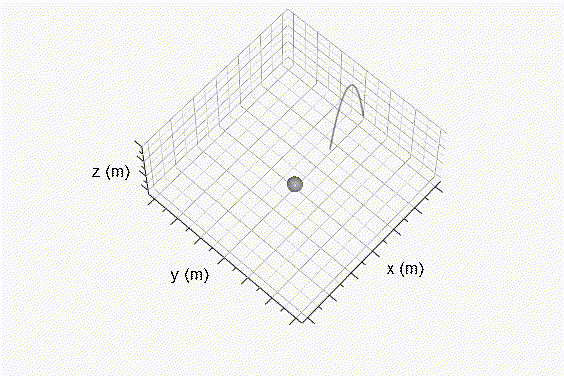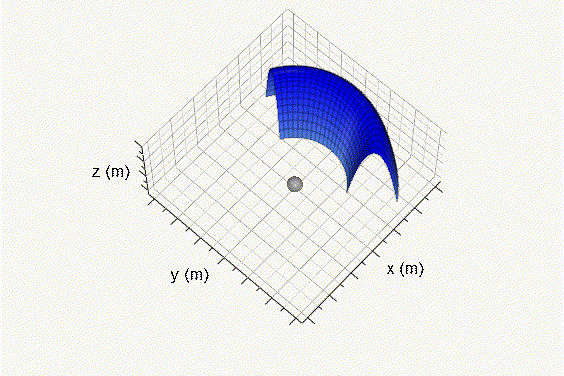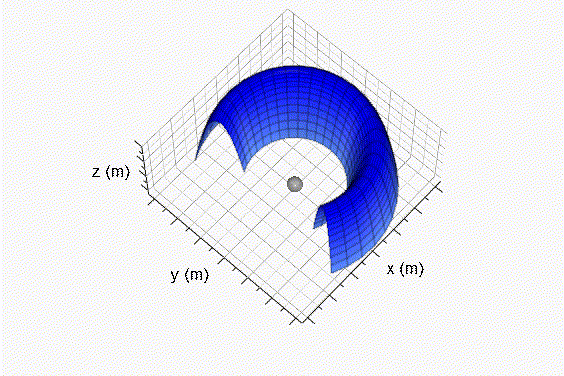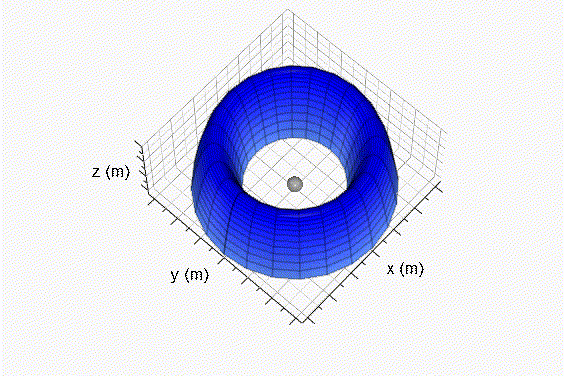
Fig. 2 Superficie de revolución generada debajo del origen de coordenadas.

Resolviendo ∀_{_v2} usando la integral del volúmen de un sólido de revolución generado por las curvas x_₁ y x_₂, dadas las Ecs. 13 y 14, respectivamente:

∀_{_v2} = π ∫ { [ x_₁(y) ]^² - [ x_₂(y) ]^² } dy

(29)

Resolviendo la integral para x_₁(y):

                            _{_{V_₂}}                                       y
∫ [ x_₁(y) ]^²dy  =   ∫ [ k  +  (0.5D - k) ( 1  -  ^____ )^{^1/2} ] dy
                            ^⁰                                        V_₂

(30)

                                             (0.5D - k)^²            y                       4k (0.5D - k) V_₂       y                     _{_V2}
∫ [ x_₁(y) ]^²dy  =   [ k^²y  -  ^___________ V_₂ ( ^____  -  1 )^²  -  ^{_______________} ( ^____  -  1 )^{^3/2} ]
                                                    2                   V_₂                               3                     V_₂                    ^⁰

(31)

Reemplazando los límites (V_₂, 0) para y en la Ec. 31 y simplificando, se obtiene:

                                              (0.5D - k)^²        4k (0.5D - k)
∫ [ x_₁(y) ]^²dy  =  V_₂ [ k^²  +  ^___________  +  ^{_____________} ]
                                                     2                       3

(32)

Resolviendo la integral para x_₂(y):

                             _{_V2}                                       y
∫ [ x_₂(y) ]^²dy  =  ∫ [ k  -  (0.5D - k) ( 1  -  ^____ )^{^1/2} ] dy
                             ^⁰                                        V_₂

(33)

                                            (0.5D - k)^²           y                      4k (0.5D - k) V_₂        y                     _{_{V_₂}}
∫ [ x_₂(y) ]^²dy  =  [ k^²y  -  ^__________ V_₂ ( ^____  -  1 )^²  +  ^{________________} ( ^____  -  1 )^{^3/2} ]
                                                  2                   V_₂                                 3                  V_₂                      ^⁰

(34)

Reemplazando los límites (V_₂, 0) para y en la Ec. 34 y simplificando, se obtiene:

                                                  (0.5D - k)^²        4k (0.5D - k)
∫ [ x_₂(y) ]^²dy  =  - V_₂ [ k^²  +  ^___________  -  ^{_____________} ]
                                                          2                        3

(35)

Reemplazando las Ecs. 32 y 35 en la Ec. 29:

                                 (0.5D - k)^²       4k (0.5D - k)                             (0.5D - k)^²       4k (0.5D - k)
∀_{_v2}  =  π V_₂ [ k^²  +  ^_________  +  ^{______________} ] -  π V_₂ [ k^²  +  ^_________  -  ^{______________} ]
                                      2                        3                                               2                       3

(36)

                         8k (0.5D - k)
∀_{_v2}  =  π V_₂ [  ^{______________} ]
                                  2

(37)

Tomando θ_₁ = (0.5D - k), y reemplazando en la Ec. 37:

                        8k θ_₁
∀_{_v2}  =  π V_₂ [  ^_______ ]
                           2

(38)

Fig. 3 Superficie de revolución generada encima del origen de coordenadas.

Reemplazando las Ecs. 28 y 38 en la Ec. 20:

           -θ_₁^²                             4k θ_₁                                                                                          8k θ_₁
π V_₂ [ ^____ ( 1  -  R_{_D}^² )  +  ^________ ( 1  -  R_{_D}^{^3/2} )  -  ( 1 - R_{_D} ) (k^²  +  θ_₂^² ) ]  =  π V_₂ [  ^_______ ]
             2                                  3                                                                                                 2

(39)

Simplificando la Ec. 39:

    -θ_₁^²                            4k θ_₁
[ ^____ ( 1  -  R_{_D}^² )  +  ^______ ( 1  -  R_{_D}^{^3/2} )  -  ( 1 - R_{_D} ) (k^²  +  θ_₂^² ) ]  =  4k θ_₁
       2                                 3

(40)

Reescribiendo la Ec. 40 en términos de d, D, y k:

  -(0.5D - k)^²       (0.5d - k)^⁴       4k (0.5D - k)     (0.5d - k)^³              (0.5d - k)^²
^__________ (1 - ^_______ )  +  ^___________ (1 - ^________ )  -  (1 - ^________ ) (k^² + (0.5D)^²)  =  4k (0.5D - k)
        2               (0.5D - k)^⁴               3               (0.5D - k)^³              (0.5D - k)^²

(41)

La Ecuación 41 tiene como parámetros de entrada: d = diámetro de la partícula, D = diámetro interno del matraz, y como parámetro de salida k = vértice de la parábola en el perfil de velocidades (Fig. 1). Como esta ecuación es implícita para k, se utiliza un método iterativo para resolverlo. Una vez que se obtiene k se utliza la Ec. 10 para calcular V_₂:

(0.5d - k)^²
V_₂ = V_₁ [ ^____________ - 1 ]^{^-1}
(0.5D - k)^²

(42)

5. EJEMPLO

Calcular la distribución de velocidades de flujo alrededor de una partícula esférica de diámetro d = 1.0 mm, la cual cae en agua en un matraz de diámetro interno D = 6.5 cm. Considerar: T = 20 °C; γ_{_s} = 2.65 gr/cm^³; γ = 1.0 gr/cm^³, y g = 9.81 m/s^².

1. Calcular la velocidad de caída de la partícula esférica, usando el programa enlineavelocidadcaida:

V_₁ = 0.155 m/s

2. Calcular k, usando la Ec. 41:

k = 0.02438 m

3. Calcular V_₂, usando la Ec. 42:

                                 [(0.001/2) - 0.02438]^²
        V_₂  =  0.155 [ ^{________________________} - 1 ]^{^-1}
                                 [(0.065/2) - 0.02438]^²

        V_₂  =  0.0203 m/s

4. Calcular 4P, usando la Ec. 7:

                           - 0.0203
        4P  =  ^{_______________________}
                    [(0.065/2) - 0.02438]^²

        4P  =  - 3.0732

5. Calcular c, usando la Ec. 6:

                                     - 0.0203
        c  =  0.02438 - [ ^___________ ]^{^1/2}
                                     - 3.0732

        c  =  0.01626 m

6. CONCLUSIONES

Se ha calculado la distribución espacial del flujo permanente alrededor de una partícula esférica que cae dentro de un matraz lleno de agua. Dados los diámetros de la partícula y el matraz, y utilizando la ley fundamental de la conservación de la masa, integrales de volúmen y el teorema del valor medio, se calcula las coordenadas del punto P_₂, el cual separa el flujo ascendente, próximo a la pared interior del matraz, del flujo descendente, adyacente a la partícula.

BIBLIOGRAFÍA

Ponce, V. M. 2014. Engineering Hydrology, Principles and Practices, Segunda Edición online.

Piskunov, N. 1977. Cálculo Diferencial e Integral, Tercera Edición, Editorial Moscú.

210425 11:11

Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader.