1. INTRODUCTION The computation of sediment transport is fraught with difficulties, including the role of friction (grain and form), armoring, flow unsteadiness, and so on. Despite these difficulties, it is usually possible in practice to develop a sediment rating curve for a given site based on an appropriate sediment transport relation and/or measured field data. The sediment rating curve is a plot of bed-material discharge (tons/day) vs water discharge (cfs), usually on a log-log scale. At high water discharges, the rating curve has a tendency to asymptotically approach a maximum sediment concentration (American Society of Civil Engineers 1975, p. 476), i.e., asymptotic to a 45° line. Ponce (1988) examined this feature of the sediment rating and referred to the maximum value as the ultimate sediment concentration. The nature of the sediment rating, where the concentration (a) increases with discharge at low discharges, and (b) is asymptotic to a maximum value at sufficiently high discharges, suggests that there is a mechanism acting to reduce the sediment concentration at low discharges. It is surmised here that this mechanism is form friction. The objective of this study is to show, using high-quality field data sets, that form friction is primarily responsible for the documented curvature and shape of the sediment rating at low discharges. Specifically, it will be confirmed that at high discharges, the sediment rating curve has a tendency to asymptotically approach a maximum sediment concentration (American Society of Civil Engineers 1975). At low discharges, form friction reduces the sediment concentration below that which could be attained if form friction were to be negligible. The net effect of form friction is to produce a drawdown of the sediment concentration below the ultimate value (Colby 1964; Ponce 1988), substantially increasing the complexity of sediment transport computations at low discharges. Einstein (1950) was apparently the first to separate total alluvial channel friction into its components: (a) grain friction, and (b) form friction. He argued that the part of the energy spent on form friction does not contribute to the bedload motion; therefore, it could be neglected in the calculation of the sediment load (op. cit., page 9). This fits admirably with our conclusion that the effect of form friction is to reduce sediment load below that which could be attained solely with grain friction. 2. THE FIELD DATA SET In this study, we used the data assembled by Williams (1995), who produced a digital database comprising data used by Ackers and White (1973), Brownlie (1981 a,b), Engelund and Hansen (1967), and Yang (1973) in the development of their sediment transport relations. In particular, the Brownlie data set included approximately 7000 sets of field and laboratory data. Williams (1995) filtered the data to include only points with the following features:
The following six sets of Brownlie's data (Brownlie 1981a, 1981b) were used for the present analysis:
Within each data set, each data unit consisted of the following:
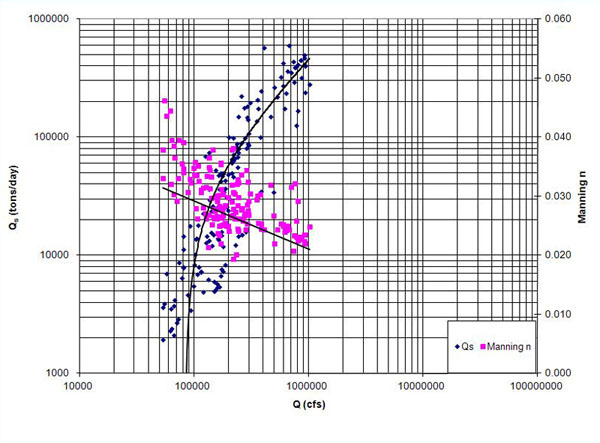
The Niobrara River data set also included bedform type. 3. METHODOLOGY AND RESULTS Measured sediment rating curves, including a graphical best fit, are shown in Figs. 1 (a) to 1 (f). In addition, for each data unit, the water discharge, channel width, hydraulic depth, and bottom slope were used to calculate Manning's n (Chow 1959). For simplicity, channel shape was assumed to be rectangular. For each data set, the calculated values of Manning's n were plotted on a secondary y-axis, so that the trend in sediment rating could be readily compared with the trend in Manning's n. In all cases, it is clearly seen that Manning n decreases as the water (and sediment) discharge increase.
4. CONCLUSIONS Using high-quality field data sets, it has been shown that form friction is largely responsible for the documented curvature and shape of typical sediment rating curves. Specifically, we have confirmed that at high discharges, sediment rating curves have a tendency to asymptotically approach a maximum sediment concentration. Conversely, at low discharges, form friction acts to reduce the sediment concentration below that which could be attained if form friction were to be negligible. Measured sediment rating curves were plotted for six high-quality data sets. In addition, for each data unit, water discharge, channel width, hydraulic depth, and bottom slope were used to calculate Manning's n. Data was plotted in such a way that the trend in sediment rating could be readily compared with the trend of Manning's n. In all cases, Manning's n decreased as the water and sediment discharge increased. It is concluded that at low discharges, form friction has a significant role in reducing sediment transport, effectively decreasing the sediment concentration substantially below the ultimate value. At high discharges, form friction is reduced, total friction tends to a constant value, and sediment concentration approaches asymptotically the ultimate value. These findings clarify current understanding of sediment rating curves in particular, and sediment transport in general.
REFERENCES
Ackers, P., and W. R. White (1973). "Sediment transport: New approach and analysis," Journal of Hydraulic Engineering, ASCE, 99(11), 2041-2060.
American Society of Civil Engineers. (1975). Sedimentation Engineering. ASCE Manuals and Reports on Engineering Practice - No. 54, New York, NY.
Brownlie, W. L. (1981a). "Prediction of flow depth and sediment discharge in open channels," Report KH-R-43A, W.M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology, Pasadena, California.
Brownlie, W. L. (1981b). "Compilation of alluvial channel data: Laboratory and field," Report KH-R-43B, W.M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology, Pasadena, California.
Chow, V. T. (1959). Open-channel Hydraulics. McGraw-Hill, New York.
Colby, B. R. and C. H. Hembree (1955). "Computations of total sediment discharge, Niobrara river near Cody, Nebraska." U.S. Geological Survey Water Supply Paper No. 1351, Washington, D.C.
Colby, B. R. (1964). "Discharge of sands and mean-velocity relations in sand-bed streams," U.S. Geological Survey Professional Paper 462-A, Washington, D.C.
Einstein, H. A. (1950). "The bed-load function for sediment transportation in open channel flows,"
Technical Bulletin No. 1026,
U. S. Dept. of Agriculture, Soil Conservation Service, Washington, D.C., September.
Engelund, F., and E. Hansen. (1967). "A monograph on sediment transport in alluvial streams," Teknisk Vorlag, Copenhagen, Denmark.
Hubbell, D. W. and D. Q. Matejka (1959). "Investigations of sediment transportation, Middle Loup river at Dunning, Nebraska." U. S. Geological Survey Water Supply Paper No. 1416, Washington, D.C.
Nordin, C. F., Jr. and J. P. Beverage (1965). "Sediment transport in the Rio Grande, New Mexico." U. S. Geological Survey Professional Paper No. 462-F, Washington,
D.C.
Ponce, V. M. (1988). "Ultimate sediment concentration." Proceedings, 1988 National Conference of Hydraulic Engineering, American Society of Civil Engineers Hydraulics Division,
New York, 311-315.
Toffaleti, F. B. (1968). "A Procedure for computation of the total river sand discharge and detailed distribution, bed to surface." Technical Report No. 5, Committee on Channel Stabilization, Corps of Engineers, United States Army, Vicksburg, Mississippi.
Williams, D. T. (1995). "Selection and predictability of sand transport relations based upon a numerical index," Ph.D. dissertation, Department of Civil Engineering, Colorado State University, Fort Collins, Colorado.
Yang, C. T. (1973). "Incipient motion and sediment transport." Journal of the Hydraulics Division, ASCE, 99(10), 1679-1704.
1
Professor, Department of Civil, Construction, and Environmental Engineering,
San Diego State University, San Diego, California 92182-1324.
|
| 150226 21:45 |