El método Muskingum-Cunge

El Método Muskingum-Cunge

Victor M. Ponce

17 Febrero 2021

Resumen. El método Muskingum-Cunge es revisado con el objetivo de fomentar su mayor aceptación en la práctica de la ingeniería hidráulica. Se revisan y aclaran sus antecedentes teóricos y su precisión computacional. El método constituye el único modelo numérico de la ecuación de la onda difusiva basado en un cálculo directo, sencillo y explícito, en el cual la solución es independente del tamaño de la malla. Ningún otro método de enrutamiento de flujo puede reclamar este conjunto de propiedades.

1. MÉTODO MUSKINGUM-CUNGE

El método Muskingum-Cunge es un método de enrutamiento del flujo de avenidas el cual mejora el método clásico de Muskingum mediante el uso de principios físicos y numéricos establecidos por Cunge (1969). A modo de comparación, se puede afirmar que si bien el método de Muskingum clásico es de naturaleza hidrológica, el método Muskingum-Cunge tiene un claro sentido hidráulico. La Tabla 1 compara ambos métodos, describiendo sus diferencias.

Tabla 1. Comparación entre los métodos de Muskingum y Muskingum-Cunge.

Criterio Muskingum Muskingum-Cunge

Año de origen 1938 1969

Referencia original
McCarthy, G. T. 1938. "The unit hydrograph and flood routing," manuscrito presentado en la Conferencia de la División Nor-Atlántica del Cuerpo de Ingenieros del Ejército de los Estados Unidos, 24 de junio.

Cunge, J. A. 1969. "On the subject of a flood propagation computation method (Muskingum Method)," Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.

Referencia
Chow, V. T. 1994. Hidráulica de Canales Abiertos. Mc-Graw Hill Interamericana S.A., página 596.

Ponce, V. M. 2014. "Método Muskingum-Cunge," Sección 10.6 del libro Fundamentos de la Hidráulica de Canales.

Naturaleza
del cálculo
Método hidrológico de enrutamiento de flujo, en el cual los parámetros K y X se calculan mediante calibración, usando aforos de hidrogramas de flujo de entrada y de salida en un tramo seleccionado del río o corriente.

Método hidráulico de enrutamiento de flujo, en el cual los parámetros K y X se calculan en base al caudal unitario, la pendiente del río o corriente, la celeridad de la onda de flujo, y la longitud del tramo siendo analizado.

La facilidad
de uso
depende de
La existencia de mediciones de hidrogramas de avenida en el tramo seleccionado, lo cual hace posible la calibración de los parámetros.

La disponibilidad de datos geométricos e hidráulicos en el tramo siendo analizado, y de la medida en que éstos son representativos del tramo.

Facilidad
de cálculo
Puede usarse con cualquier herramienta computacional, incluida hoja de cálculo, programación digital, y software comercial y gubernamental disponible.

Puede usarse con cualquier herramienta computacional, incluida hoja de cálculo, programación digital, y software comercial y gubernamental disponible.

Precisión
Apropiada para el tramo y evento de avenida utilizados en la calibración de los parámetros; reducida para cualquier otro tramo y/o evento.

Apropiada para cualquier evento en el tramo en consideración; sólo limitado en la medida en que los datos geométricos e hidráulicos son representativos del tramo.

Enrutamiento
no lineal
Muy limitado; usualmente no disponible debido a la necesidad de gran cantidad de datos.

Disponible si se considera necesario, pero a costo de una mayor complejidad en el cálculo.

Conclusiones
Método anticuado; precisión muy limitada en los casos de extensos enrutamientos en aplicaciones a escala de cuenca.

Método moderno, que está de acuerdo con los desarrollos más recientes en modelado numérico; apropiado para extensos enrutamientos en aplicaciones a escala de cuenca.

Dados los conceptos descritos en la Tabla 1, se concluye que el método Muskingum-Cunge es teóricamente más apropiado que el método Muskingum, particularmente para extensas aplicaciones de enrutamiento a escala de cuenca. Por lo tanto, se recomienda su uso en la práctica del modelado de ingeniería hidráulica e hidrológica, con alcance a nivel global.

2. MUSKINGUM-CUNGE Y FLUJOS DE AVENIDA

La clave para comprender el fundamento teórico del método Muskingum-Cunge es el reconocimiento de que la onda difusiva es aplicable a través de un rango más amplio que los correspondientes a las ondas cinemáticas y dinámicas, respectivamente (Ponce y Simons, 1977). Las ondas cinemáticas no se atenúan, mientras que la mayoría de las ondas de inundación se atenúan al menos un poco; por otro lado, las ondas dinámicas se atenúan demasiado y, por lo tanto, no representan ondas de inundación en los casos típicos. La onda difusiva se encuentra en el rango medio de atenuación; por lo tanto, es la onda más aplicable desde el punto de vista práctico.

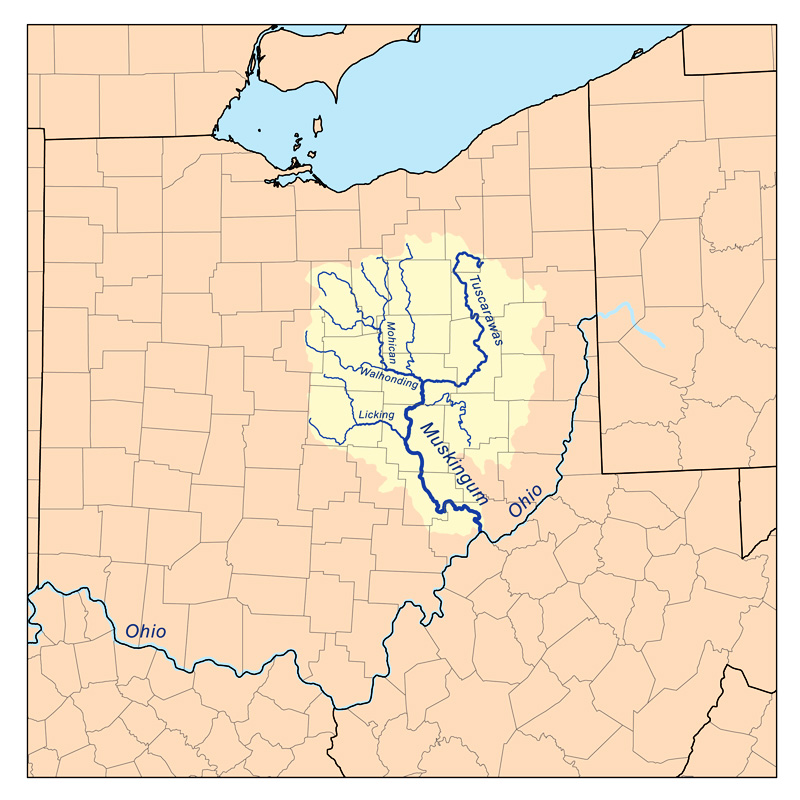
Este hecho fue reconocido por McCarthy en 1938 (Fig. 1) (Chow, 1959), y posteriormente por Cunge en 1969. Sin embargo, a diferencia de McCarthy, Cunge vinculó el método Muskingum a las propiedades de la onda difusiva. De esta manera, Cunge hizo posible relacionar los parámetros de enrutamiento del método a las características geométricas e hidráulicas del tramo en consideración.

Fig. 1 El río Muskingum cerca de Marietta, Ohio, EE.UU.

Dada la simplicidad del método Muskingum-Cunge (M-C), particularmente cuando se compara con métodos alternativos de enrutamiento hidráulico, el método M-C sigue siendo un fuerte candidato entre la gama de modelos de enrutamiento. Éste es particularmente el caso en vista de que los métodos de enrutamiento hidráulico son decididamente inadecuados para aplicaciones hidrológicas a escala de cuenca. Por lo tanto, el método M-C es el único modelo de enrutamiento de ondas difusivas lo suficientemente simple y preciso como para prestarse al modelado hidrológico a gran escala. En este trabajo se explican en detalle los argumentos que justifican esta afirmación.

3. MUSKINGUM-CUNGE Y PRECISIÓN COMPUTACIONAL

La ventaja del método Muskingum-Cunge es su directa relación con la onda difusiva. Cunge demostró fehacientemente que el método Muskingum y un esquema numérico similar de la onda cinemática tienen la misma base teórica. Además, Cunge calculó el error del esquema numérico de primer orden (es decir, el método de Muskingum), eventualmente vinculando este error al coeficiente de difusividad de la onda difusiva (Hayami, 1951). Este logro propició el camino para el cálculo de los parámetros de enrutamiento en función de variables geométricas e hidráulicas, evitando así la necesidad de las costosas y poco prácticas mediciones de caudal.

El método Muskingum-Cunge tiene una alta precision debido a su sólida base teórica. Sus propiedades numéricas, incluidas estabilidad y convergencia, han sido ampliamente documentadas tanto en la teoría como en la práctica (Ponce y Vuppalapati, 2016). El método es fuertemente estable y con excelentes propiedades de convergencia para valores del número de Courant C ≅ 1. Estas propiedades singulares de fuerte estabilidad y excelente convergencia aseguran su independencia de la malla, es decir, la propiedad de un esquema numérico de reproducir el mismo resultado para cualquier tamaño de la malla. Los métodos competitivos (numéricos), incluida el de la onda cinemática, carecen de esta propiedad, lo que pone en duda su corrección teórica (Ponce, 1986).

En resumen, el método Muskingum-Cunge es el único modelo numérico de la ecuación de la onda difusiva basado en un cálculo sencillo, explícito, y con el resultado siendo independente del tamaño de la malla. Ningún otro método de enrutamiento de flujo (de avenidas) posée este conjunto de propiedades.

4. ECUACIONES DE ENRUTAMIENTO

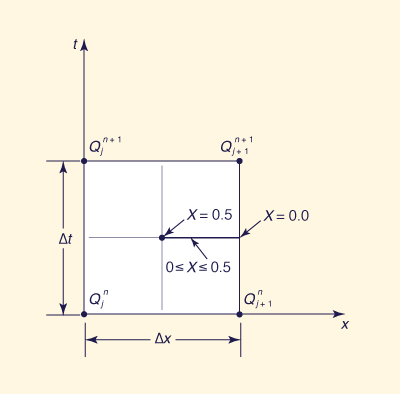
La ecuación básica del método Muskingum-Cunge es la siguiente (Fig. 2):

Fig. 2 Definition sketch.

_{_{n + 1}} _{_{n + 1}} _{_n} _{_n}
Q _{_{j + 1}} = C_₀Q_{_j} + C_₁Q_{_j} + C_₂Q_{_{j + 1}}

(1)

en la cual j = índice espacial, n = índice temporal, y C₀, C₁ y C₂ se calculan de la siguiente manera:

Δt - 2KX
C_₀ = ^{__________________}
2K (1 - X ) + Δt

(2)

Δt + 2KX
C_₁ = ^{_____________________}
2K (1 - X ) + Δt

(3)

2K (1 - X ) - Δt
C_₂ = ^{_____________________}
2K (1 - X ) + Δt

(4)

Los parámetros K and X se calculan con las siguientes formulas (Cunge, 1969; Ponce, 2014):

Δx
K = ^____
c

(5)

1 q
X = ^___ ( 1 - ^__________ )
2 S_{_o} c Δx

(6)

en las cuales: Δx = longitud de tramo (intervalo de espacio); c = celeridad de la onda difusiva; q = caudal unitario; y S_{_o} = pendiente del río o corriente.

5. ENRUTAMIENTO LINEAL VS NO LINEAL

En la naturaleza, las ondas de avenida generalmente exhiben un comportamiento no lineal, es decir, su propiedades de celeridad y atenuación tienden a variar con el flujo. La magnitud de este efecto varía con la forma de la sección transversal de manera predecible. Al respecto, se reconocen tres formas asintóticas de sección transversal (Ponce, 2014):

Hidráulicamente ancha,

Triangular, e

Inherentemente estable.

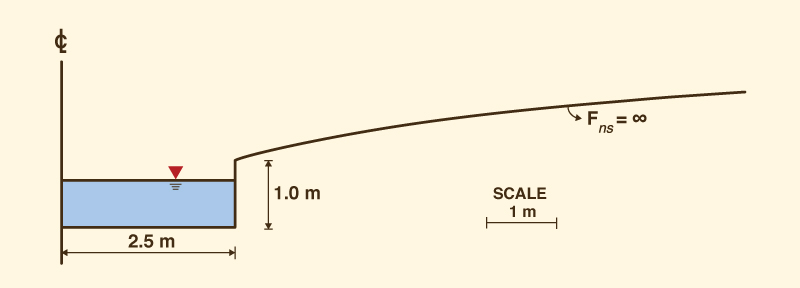
El canal inherentemente estable es aquél en el cual el radio hidráulico es una constante en la zona de desborde (Fig. 3). La forma del canal inherentemente estable ha sido establecida por Ponce y Porras (1995).

Fig. 3 Sección transversal típica de un canal inherentemente estable.

Se puede demostrar que el efecto no lineal de empinamiento es más fuerte para canales hidráulicamente anchos, débil para canales triangulares y totalmente inexistente para canales inherentemente estables. En la práctica, es probable que la mayoría de las sección transversales estén cerca de ser hidráulicamente anchas. Por lo tanto, el efecto no lineal puede ser bastante marcado en algunos casos.

Existen dos formas de calcular los parámetros en el enrutamiento Muskingum-Cunge (Ponce y Yevjevich, 1978):

Método lineal, y
Método no lineal.

En el método lineal, los parámetros de enrutamiento K y X se basan en variables hidráulicas promedio (o representativas) (c y q) y se mantienen constantes durante todo el cálculo. En el método no lineal, se permite que los parámetros de enrutamiento varíen con el flujo, es decir, que varíen para cada celda computacional en función de las variables de flujo locales. La Tabla 2 describe la comparacion entre los enrutamientos lineal y no lineal del método Muskingum-Cunge.

Tabla 2. Comparacion entre los enrutamientos lineal y no lineal
del método Muskingum-Cunge.

Criterio Método lineal Método no lineal

General
Los parámetros de enrutamiento se mantienen constantes.

Los parámetros de enrutamiento varían con el flujo.

Conservación de masa
No hay pérdida de masa (volumen).

Pequeña pérdida perceptible de masa, usualmente menor del 1%.

Grado de dificultad
Fácil.

Comparativamente más difícil.

Campo de aplicación
En la ingeniería práctica.

En la investigación y otras aplicaciones especializadas.

6. RECOMENDACIONES

El método Muskingum-Cunge representa una mejora considerable en la precisión computacional, en comparación con el método Muskingum convencional. La única salvedad es que el cálculo de los parámetros (Ecuaciones 5 y 6) debe basarse en valores de celeridad de la ola de crecida c y descarga unitaria q que sean lo suficientemente representativos del tramo en consideración. Para lograr este objetivo, se recomienda que se utilicen datos geométricos e hidráulicos respaldados por SIG para estimar mejor las variables en las cuales se base el cálculo de los parámetros de enrutamiento.

7. RESUMEN

El método Muskingum-Cunge es revisado con el objetivo de fomentar su mayor aceptación en la práctica de la ingeniería hidráulica. Se revisan y aclaran sus antecedentes teóricos y su precisión computacional. El método constituye el único modelo numérico de la ecuación de la onda difusiva basado en un cálculo directo, sencillo y explícito, en el cual la solución es independente del tamaño de la malla. Ningún otro método de enrutamiento de flujo puede reclamar este conjunto de propiedades.

REFERENCIAS BIBLIOGRÁFICAS

Chow, V. T. 1959. Open-channel Hydraulics. Mc-Graw Hill, New York.

Cunge, J. A. 1969. On the Subject of a Flood Propagation Computation Method (Muskingum Method), Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.

Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, December.

McCarthy, G. T. 1938. The Unit Hydrograph and Flood Routing. Unpublished manuscript, presented at a Conference of the North Atlantic Division, U.S. Army Corps of Engineers, June 24.

Natural Environment Research Council. 1975. Flood Studies Report. Vol. 3: Flood Routing. London. England.

Ponce, V, M., and D. B. Simons. 1977. Shallow wave propagation in open-channel flow. Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, December, 1461-1476.

Ponce, V. M., and V. Yevjevich. 1978. Muskingum-Cunge method with variable parameters. Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY12, December, 1663-1667.

Ponce, V. M. 1986. Diffusion Wave Modeling of Catchment Dynamics. Journal of Hydraulic Engineering, ASCE, Vol. 112, No. 8, August, 716-727.

Ponce, V. M., and P. J. Porras. 1995. Effect of cross-sectional shape on free-surface instability. Journal of Hydraulic Engineering, ASCE, Vol. 121, No. 4, April, 376-380.

Ponce, V. M. 2014. Fundamentals of open-channel hydraulics. Online textbook.

Ponce, V. M., and B. Vuppalapati. 2016. Muskingum-Cunge amplitude and phase portraits with online computation. Online article.

APÉNDICE: Origen del érmino Muskingum-Cunge

En un contexto hidrológico, la palabra "Muskingum" se toma del río Muskingum, en el este del estado de Ohio, EE.UU. La palabra proviene del idioma nativo americano de Delaware que suena similar, que algunos afirman que se traduce como "Ojo de alce". El término "método Muskingum" fue utilizado por primera vez por G. T. McCarthy en un manuscrito fechado en 1938 y posteriormente referido por Chow (1959). McCarthy probó su nuevo método hidrológico de enrutamiento de inundaciones usando datos del río Muskingum; de ahí el nombre.

Jean A. Cunge

La palabra "Cunge" reconoce a Jean A. Cunge, ingeniero polaco-francés que, en 1969, publicó las ecuaciones utilizadas en el nuevo método. El nombre compuesto Muskingum-Cunge aparentemente se utilizó por primera vez en 1975 en el Informe de Estudios de Inundaciones, publicado por el Consejo de Investigación del Medio Ambiente Natural, Londres, Inglaterra. En 1990, el método Muskingum-Cunge fue incorporado al modelo HEC-1 del Cuerpo de Ingenieros del Ejército de los EE.UU., Versión 4. En 1998, HEC-1 fue la base del modelo HEC-HMS, hoy ampliamente usado en la práctica.

210216 23:15