El modelo de flujo de base de Rorabaugh (1963) se utiliza para estimar parámetros regionales de acuíferos
en la cuenca del río Papaloapan, ubicada en el sur de México.
Ésta es una cuenca tropical extensa, con un área de 46,527 km2,
una gran diversidad de condiciones climáticas, y una importante interacción
entre la hidrología superficial y la hidrología subterránea. Se han utilizado curvas de recesión de caudales
para calcular el tiempo
de almacenamiento, la constante de la cuenca, y la difusividad hidráulica del acuífero, en diez (10) puntos localizados
a lo largo y ancho de la cuenca. Los resultados preliminares muestran un acuerdo razonable entre los parámetros calculados
y los correspondientes parámetros hidrogeológicos
obtenidos del bombeo y la cartografía.
1. INTRODUCCIÓN En la hidrología de agua subterránea hay necesidad de estimar los parámetros del acuífero, tales como el tiempo de almacenamiento (Hall 1968; Ponce 1989), la constante de la cuenca (Rorabaugh y Simons 1966), y la difusividad hidráulica (Freeze y Cherry 1979). Es posible estimar estos parámetros utilizando la recesión del flujo de base, mediante el uso de la fórmula de Rorabaugh y Simons (1966). Rorabaugh (1963) convirtió la ecuación de difusión de calor a unidades de flujo de agua subterránea, haciendo posible de esta manera relacionar el flujo de base con los parámetros del acuífero. En este trabajo hemos aplicado el modelo de Rorabaugh a la recesión del hidrograma en la cuenca del río Papaloapan, en el sur de México. El objetivo es mostrar que se pueden utilizar datos de aforos de alta calidad para estimar parámetros del acuífero, ligando de esta manera los procesos de agua superficial y agua subterránea. Estas estimaciones complementan aquéllas obtenidas mediante pruebas de bombeo, pudiendo eventualmente ser usadas en ausencia de éstas (Moore 1992). 2. EL MODELO DE RORABAUGH Rorabagh (1963) desarrolló un modelo teórico del flujo de agua subterránea a una corriente, asumiendo una cuenca homogénea, isotrópica, y uniforme, es decir, con conductividad hidráulica, coeficiente de almacenamiento, y espesor del acuífero constantes. La ecuación es:
en la cual q = descarga de agua subterránea,
por unidad de longitud de la corriente,
de un lado solamente;
Utilizando la ecuación de Darcy, se puede demostrar que la cantidad
en la cual Q = flujo de base en el tiempo t; y Qo = flujo de base en el tiempo t = 0. Trainer y Watkins (1974) han usado el modelo de Rorabaugh para estimar transmisibilidades en la cuenca del río Alto Potomac. Estudios más recientes han aplicado el modelo de Rorabaugh para estimar la recarga de agua subterránea en varios escenarios hidrogeólogicos (Rutledge y Daniel 1994; Mau y Winter 1997; Sanz 1997). En este estudio aplicamos el modelo de Rorabaugh para estimar las características del acuífero en una cuenca tropical grande, caracterizada por una gran diversidad de escenarios hidrogeológicos y climáticos. 3. CARACTERÍSTICAS DEL ACUÍFERO Boussinesq (1877) linearizó la ecuación de flujo de agua subterránea, expresándola en forma de una ecuación de difusión, la cual puede ser resuelta en forma más conveniente (Hall 1968). Con la analogía de difusión, una cuenca de agua subterránea (manto acuífero) puede ser caracterizada en términos de los siguientes parámetros: 1. Tiempo de almacenamiento ts (Hall 1968; Ponce 1989; Tallaksen 1995), una constante de recesión igual a:
El tiempo de almacenamiento es tal que cuando t = ts, la descarga se ha reducido al 37% del valor correspondiente a t = 0, es decir, es una medida de la velocidad relativa de la recesión del hidrograma. 2. Constante de cuenca Kb (Rorabaugh y Simons 1966):
La constante de cuenca Kb (en unidades de T -1) combina la propiedades geométricas e hidrogeológicas del acuífero. 3. Difusividad hidráulica D (Freeze y Cherry 1979):
La difusividad hidráulica (en unidades L2 T -1) combina las propiedades hidrogeológicas del acuífero en un parámetro que caracteriza el proceso de difusión.
4. APLICACIÓN A LA CUENCA DEL RÍO PAPALOAPAN
El modelo de Rorabaugh fue aplicado a la recesión del hidrograma en la cuenca del río Papaloapan,
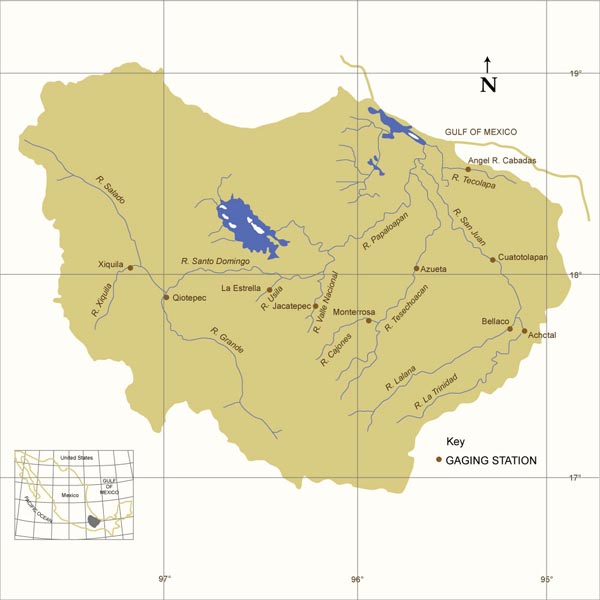
en los estados de Veracruz y Oaxaca, México (Fig. 1).
Esta cuenca es extensa, de 46,517 km2, con una gran variedad
de escenarios hidrogeológicos y climáticos.
El Cuadro 1 muestra diez (10) estaciones de aforo seleccionadas, nombre de la corriente o río,
localización geográfica,
precipitación media anual y propiedades geométricas de la cuenca.
La longitud hidráulica, es decir, la longitud medida a lo largo de la corriente principal, se obtuvo de mapas
topográficos.
El ancho del acuífero se estimó como la relación de área de drenaje dividida por la longitud
hidráulica. Las condiciones climáticas varían de hiperhúmedo a árido; por ejemplo,
río Usila en La Estrella, con 4,805 mm de precipitación media anual,
al río Xiquila en Xiquila, con 354 mm.
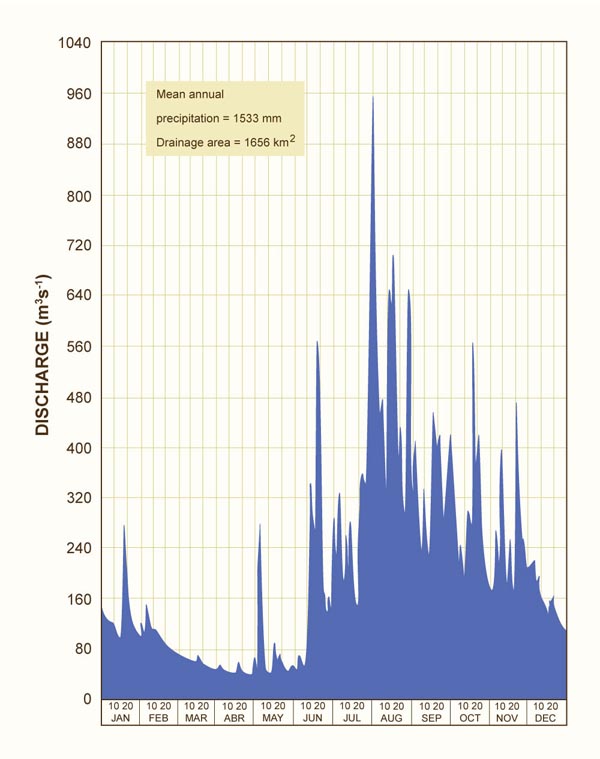
La Figura 2 muestra un hidrograma típico
de la cuenca del río Papaloapan, el del río Tesechoacán en Azueta
(Comisión del Papaloapan 1972).
Para las diez estaciones seleccionadas, se coleccionaron los datos de recesión del hidrograma para el período de dos años 1971-72. Para cada estación, se seleccionaron varios períodos de recesión del hidrograma, con duraciones de 5 a 18 días. Para cada período, se calcularon valores medios diarios de: (a) tiempo de almacenamiento, (b) constante de la cuenca, y (c) difusividad hidráulica. Para cada estación, los valores medios de cada período se utilizaron para calcular un valor promedio correspondiente a la estación.
El Cuadro 2 muestra los parámeteros de acuífero calculados
para las diez (10) estaciones
seleccionadas, las cuales comprenden una gran diversidad de escenarios hidrogeológicos
y climáticos. El tiempo de almacenamiento varía entre
23.49 and 116.64 días; la constante de la cuenca varía entre
0.00347 and 0.01725 días -1; la difusividad hidráulica
varía entre 0.058 and 15.619 km2 día -1.
El Cuadro 3 muestra las rocas predominantes, las cuales varían desde rocas ígneas
(basaltos) a sedimentarias (areniscas, calizas)
a metamórficas (esquisto) (Mapa Geológico de México, escala
1:250,000, publicado por INEGI).
El Cuadro 4 muestra los tipos de roca predominantes
agrupados en base al tiempo de almacenamiento.
El Grupo I Grupo I (Jacatepec, La Estrella, Monterrosa, y Quiotepec) consiste de subcuencas con un tiempo de almacenamiento relativamente corto (23 a 35 días). Estas subcuencas están localizadas lejos de la costa, en dirección sur a sureste (Fig. 1), a través de las montañas, con climas que varían de hiperhúmedo a árido, y consistiendo primeramente de rocas metamórficas, con la presencia de algunas rocas sedimentarias. Estos acuíferos drenan en forma relativamente rápida. El Grupo II (Angel R. Cabadas) consiste de una cuenca con tiempo de almacenamiento intermedio (46 días). Esta subcuenca está localizada en la costa, hacia el noreste, presentando un clima húmedo y rocas basálticas. El Grupo III (Achotal, Azueta, Bellaco, y Cuatotolapan) consiste de subcuencas con un tiempo de almacenamiento relativamente largo (51 a 69 días). Estas subcuencas están localizadas en las llanuras del este, con clima húmedo y mayormente rocas sedimentarias y algunas metamórficas. El Grupo IV (Xiquila) consiste de una cuenca con un tiempo de almacenamiento muy largo (116 días). Esta subcuenca está localizada lejos de la costa, en dirección suroeste, drenando la Sierra Madre, con un clima árido, y mayormente rocas sedimentarias y algunas rocas volcánicas. Los acuíferos del Grupo I, donde predomina el esquisto, son incapaces de mantener flujos de base por períodos largos. Contrariamente a esto, en el Grupo IV, donde predomina la caliza, el acuífero es capaz de mantener flujos de base por períodos relativamente largos. 5. VERIFICACIÓN DE CAMPO El Cuadro 5 muestra datos geográficos e hidrogeológicos en siete (7) pozos localizados en la cuenca del río Papaloapan. Los valores de difusividad hidráulica, aunque restringidos a la parte norte-centro de la cuenca, se comparan favorablemente en forma preliminar con aquéllos mostrados en el Cuadro 2. La ausencia de datos en otras partes de la cuenca no permite una comparación más exhaustiva.
6. CONCLUSIONES El modelo de Rorabaugh se ha utilizado para estimar parámetros regionales de acuíferos en la cuenca del río Papaloapan, localizada en los estados de Veracruz y Oaxaca, en el sur de México. Se han calculado el tiempo de almacenamiento, la constante de la cuenca, y la difusividad hidráulica para diez (10) subcuencas. Los resultados muestran un acuerdo razonable con la geología local (extraída de mapas geológicos) y las pruebas de bombeo disponibles. Esta experiencia subraya la promesa de este método para estimar parámetros regionales de acuíferos utilizando los datos de recesión del hidrograma. BIBLIOGRAFÍA Boussinesq, J. 1877. Essai sur la theories des eaux courantes. Memoires presentes par divers savants a l'Academic des Sciences de l'Institut National de France, Tome XXIII,No. 1. Comisión del Papaloapan. 1972. Boletín Hidrométrico No. 19: 1971-1972. Secretaría de Recursos Hidráulicos, Mexico City, Mexico. Freeze, R. A., and Cherry. J. A. 1979. Groundwater. Prentice Hall, Englewood Clis, New Jersey. Hall, F. R. 1968. Base-flow recessions - A review. Water Resources Research, 4(5), 973-983. Mau, D. P., and Winter, T. C. 1997. Estimating groundwater recharge from streamflow hydrographs for a small mountain watershed in a temperate humid climate, New Hampshire, USA. Ground Water, 35(2), March-April, 291-304. Moore, G. K. 1992. Hydrograph analysis in a fractured rock terrain. Ground Water, 30(3), May-June, 390-395. Ponce, V. M. 1989. Engineering Hydrology: Principles and Practices. Prentice Hall, Englewood Cliffs, New Jersey. Rorabaugh, M. I. 1963. Estimating changes in bank storage in groundwater contributions to streamflow. International Association of Scientic Hydrology, Publication No. 63, 432-441. Rorabaugh, M. I., and Simons, W. D. 1966. Exploration of methods of relating groundwater to surface water, Columbia river basin - second phase. U.S. Geological Survey Open-file Report, March. Rutledge, A. T., and Daniel, III, C. C. 1994 Testing an automated method to estimate groundwater recharge from streamflow records. Ground Water, 32(2), March-April, 180-189. Sanz Pérez, E. 1997. Estimation of basinwide recharge rates using springflow, precipitation,and temperature data. Ground Water, 35(6), November-December, 1958-1965. Tallaksen, L. M. 1995. A review of baseflow recession analysis. Journal of Hydrology, 165,349-370. Trainer, F. W., and Watkins Jr., F. A. 1974. Use of base-runoff recession curves to determine real transmissivities in the Upper Potomac River Basin. U.S. Geological Survey Journal of Research, 2(1), 125-131.
1
Profesor de Ingeniería Civil y Ambiental,
Universidad Estatal de San Diego, California.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 130515 18:15 |