XXVII CONGRESO LATINOAMERICANO DE HIDRAULICA

Lima, Perú



COMPARACIÓN ENTRE MODELOS DE FLUJO
DE AGUA SUPERFICIAL


Luis A. Magallón y Victor M. Ponce

28 Septiembre 2016


1

INTRODUCCIÓN

El flujo de agua superficial de lámina es la escorrentía que se produce en la superficie de la Tierra sin haberse concentrado aún en canales de flujo unidimensional.

Este tipo de flujo es la primera manifestación de la escorrentía superficial, ya que esta última se produce primero como flujo superficial de lámina, para eventualmente concentrarse en corrientes unidimensionales bien definidas.

La teoría de flujo superficial de lámina utiliza un enfoque determinístico para describir el flujo superficial de lámina.

La teoría está basada en principios de la mecánica de fluidos, tales como flujo laminar y turbulento, conservación de la masa y cantidad de movimiento, y flujo no permanente.

La descripción espacial y temporal conduce a ecuaciones diferenciales y a su solución por métodos numéricos.

En este trabajo se comparan tres modelos de flujo de agua superficial:

  1. ONLINEOVERLAND, desarrollado por el Dr. Victor Miguel Ponce, de la Universidad Estatal de San Diego, California.

  2. SWMM, de la Agencia de Protección del Medio Ambiente de los EE.UU. (EPA).

  3. HEC-HMS, del Centro de Ingeniería Hidrológica del Cuerpo de Ingenieros del Ejército de los EE.UU., Davis, California (HEC).

Los modelos se compararon mediante corridas de prueba, especificando los mismos datos de entrada:

  1. Características de la tormenta,

  2. Características de la cuenca,

  3. Abstracciones hidrológicas, y

  4. Parámetros hidráulicos.

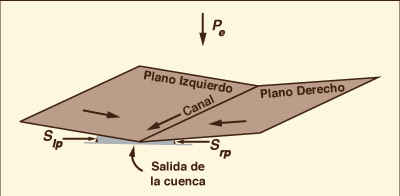
La cuenca se modela como un libro abierto, en el cual la escorrentía de uno o dos planos rectangulares drena lateralmente hacia un canal central, y éste drena finalmente hacia la boca, es decir, hacia el lugar de salida de la cuenca.

esquema de libro abierto

 Fig. 1  Esquema de libro abierto.

ONLINEOVERLAND es un modelo de flujo superficial de lámina el cual simula la dinámica de la escorrentía usando el concepto de onda difusiva (Ponce, 1986).

SWMM fue desarrollado en 1971 por la Agencia de Protección Ambiental de los EE.UU. (EPA), Metcalf and Eddy, y la Universidad de Florida.

HEC-HMS fue desarrollado y es mantenido por el Centro de Ingeniería Hidrológica del Cuerpo de Ingenieros de los EE.UU., con sede en Davis, California.

2

CORRIDAS DE COMPARACIÓN

Los modelos se corrieron bajo tres casos:

  1. Impermeable: Número de la curva CN = 100, y precipitación total P = 24 cm.

  2. Permeable: CN = 80, P = 24 cm, y, por consiguiente, precipitación efectiva Pe = 17.7666 cm (Ponce, 2010).

  3. Impermeable modificado: CN = 100, y P = 17.7666 cm.

El área de la cuenca es A = 18 ha y la duración de la tormenta es tr = 12 hr.

A.   Caso Impermeable

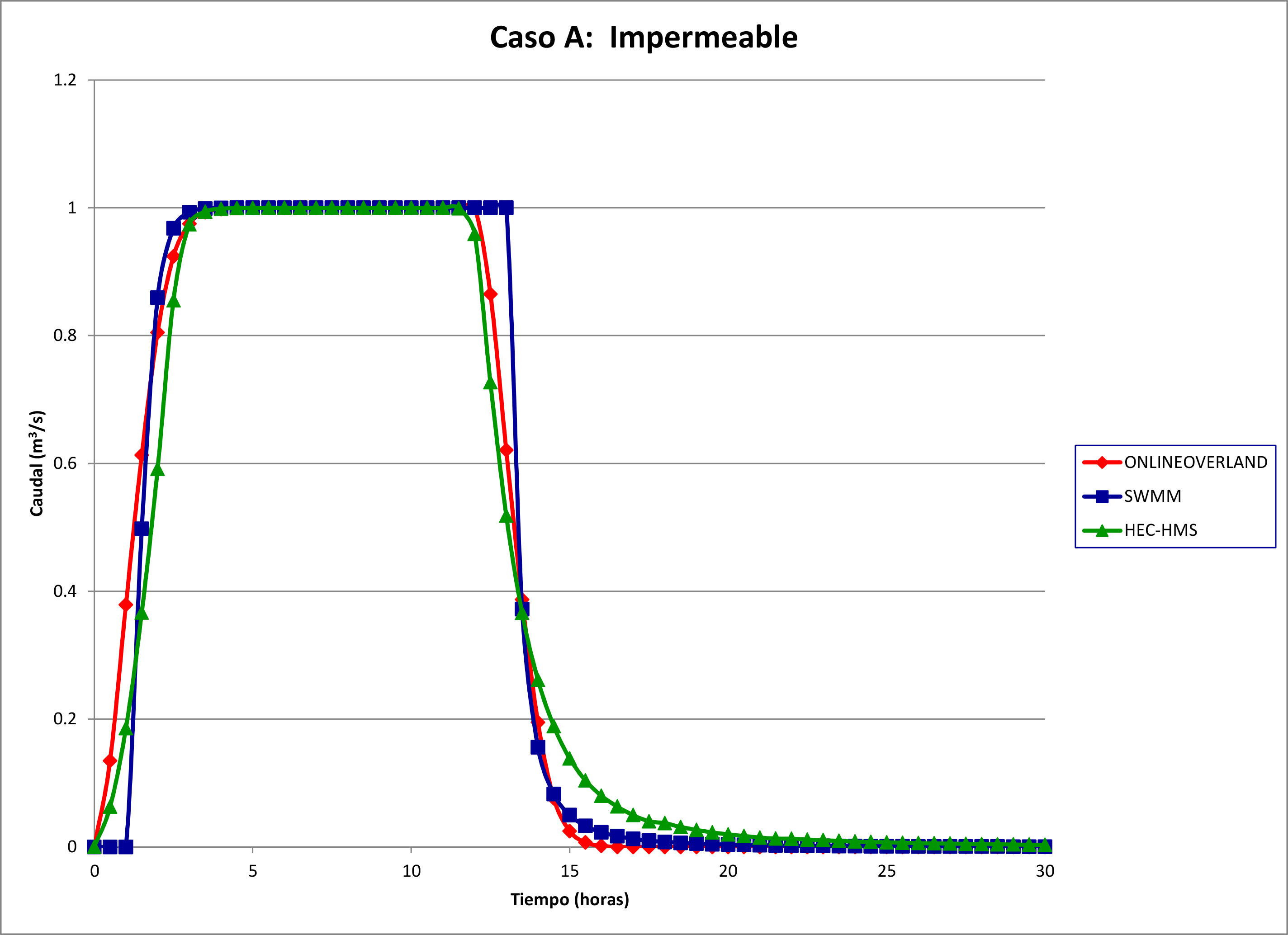
La Figura 2 muestra los hidrogramas de salida para este caso. Se elaboran las siguientes conclusiones:

  1. Caudal pico:  Los tres hidrogramas alcanzaron el caudal pico esperado, el cual, utilizando el concepto de concentración de escorrentía, es (Ponce, 2014):

    Qp = I A = (P / tr) A

    en el cual I = intensidad de precipitación total, A = área de la cuenca, P = precipitación total, and tr = duración de la tormenta. En este caso:

    Qp = (24 cm / 12 hr) × 18 ha × 0.01 m/cm × 10,000 m2/ha / (3600 s/hr) = 1 m3/s.

  2. Duración al pico:  Los tres hidrogramas mostraron pequeñas variaciones en la duración al pico. Se observó lo siguiente:

    • ONLINEOVERLAND se comportó tal como era esperado.

      El inicio de la subida del hidrograma y el inicio del receso coincidieron exactamente con el inicio y fin de la tormenta, respectivamente; vé.

    • En SWMM, la subida del hidrograma mostró un desfazamiento (es decir, una demora) finito y apreciable.

      Además, el receso del hidrograma comenzó un tiempo apreciable después de terminar la tormenta (tr = 12 hr).

      Cabe anotar que en este caso (impermeable), el inicio de la subida del hidrograma debe coincidir con el comienzo de la tormenta, y el inicio del receso con el fin de la tormenta.

    • HEC-HMS fue algo lento en la subida del hidrograma, por lo tanto, para conservar masa, fue también lento al final del receso.

      Además, el receso del hidrograma comenzó un poco antes de terminar la tormenta (tr = 12 hr).

      Cabe anotar que en este caso (impermeable), el inicio del receso debe coincidir exactamente con el fin de la tormenta.

  3. Conservación de la masa:   El volumen subtendido por el hidrograma es:

    V = P A

    En este caso:

    V = 24 cm × 18 ha × 0.01 m/cm × 10,000 m2/ha = 43,200 m3

    Para cada modelo, el volumen del hidrograma se calculó utilizando la regla de Simpson. Los volúmenes son:

    • ONLINEOVERLAND:  43,200 m3, lo cual es exactamente igual al volumen esperado.

    • SWMM:  43,376 m3, es decir, un poco más del volumen esperado, con una relación volumen calculado/volumen esperado igual a 1.0041.

    • HEC-HMS:  43,305 m3, es decir, un poco más del volumen esperado, con una relación 1.0024.

    Se concluye que sólo ONLINEOVERLAND conserva la masa exactamente, mientras que SWMM y HEC-HMS no lo hacen en forma exacta.

Outflow Hydrographs CN 100

 Fig. 2  Caso A: Impermeable.

B:  Caso Permeable

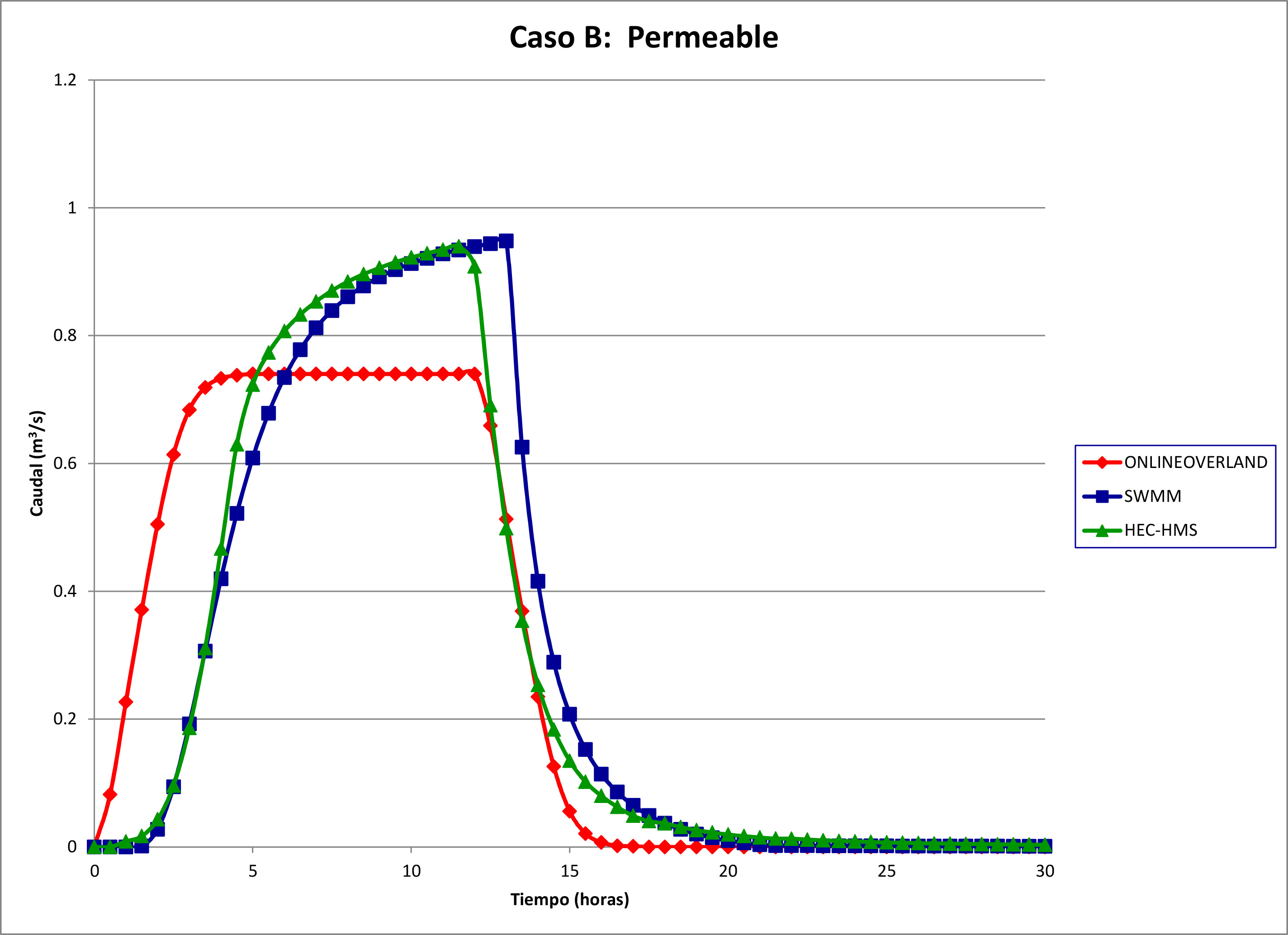
La Figura 3 muestra los hidrogramas de salida para este caso. Se elaboran las siguientes conclusiones:

  1. Caudal pico: El caudal pico, asumiendo una abstracción constante en el tiempo, es:

    Qp = Ie A = (Pe / tr) A

    en la cual Ie = intensidad de precipitación efectiva , A = área de la cuenca, Pe = precipitación efectiva, and tr = duración de la tormenta. En este caso:

    Qp = (17.7666 cm / 12 hr) × 18 ha × 0.01 m/cm × 10,000 m2/ha / (3600 s/hr) = 0.740 m3/s.

    ONLINEOVERLAND: se comportó tal como se esperaba para este caso permeable.

    Sin embargo, SWMM y HEC-HMS excedieron el caudal pico esperado de acuerdo al concepto de concentración de la escorrentía.

    Esto se debe a que ambos modelos simulan una abstracción inicial, la cual debe ser satisfecha antes de que comience la escorrentía.

    Para conservar la masa, el caudal pico debe por fuerza exceder el caudal pico esperado asumiendo una abstracción constante en el tiempo.

  2. Duración al pico:  Los tres hidrogramas mostraron diferencias en la duración al pico. Se hacen las siguientes observaciones:

    • ONLINEOVERLAND se comportó como se esperaba, asumiendo abstracción constante.

    • Como en el Caso A, SWMM mostró un desfazamiento del hidrograma en la subida y en el receso. Cabe notar que el inicio del receso debe coincidir con el fin de la tormenta, lo cual claramente no sucede con SWMM.

    • HEC-HMS mostró un desfazamiento en la subida del hidrograma, pero no en el receso. Esto último está de acuerdo con la mecánica del problema.

  3. Conservación de la masa:  El volumen subtendido por el hidrograma es:

    Ve = Pe A

    En este caso:

    Ve = 17.7666 cm × 18 ha × 0.01 m/cm × 10,000 m2/ha = 31,980 m3

    Para cada modelo el volumen del hidrograma se calculó utilizando la regla de Simpson. Los volúmenes son:

    • ONLINEOVERLAND:  31,979 m3, lo cual es 0.99997 ≅ 1.0000 del volumen esperado.

    • SWMM:  32,084 m3, es decir, un poco más del volumen esperado, con una relación 1.0033.

    • HEC-HMS:  31,749 m3, es decir, un poco menos del volumen esperado, con una relación 0.9928.

    Se concluye que sólo ONLINEOVERLAND conserva la masa exactamente, mientras que SWMM y HEC-HMS no conservan exactamente la masa.

    Outflow Hydrographs CN 80

    Fig. 3  Caso B: Permeable.

C:  Caso impermeable modificado

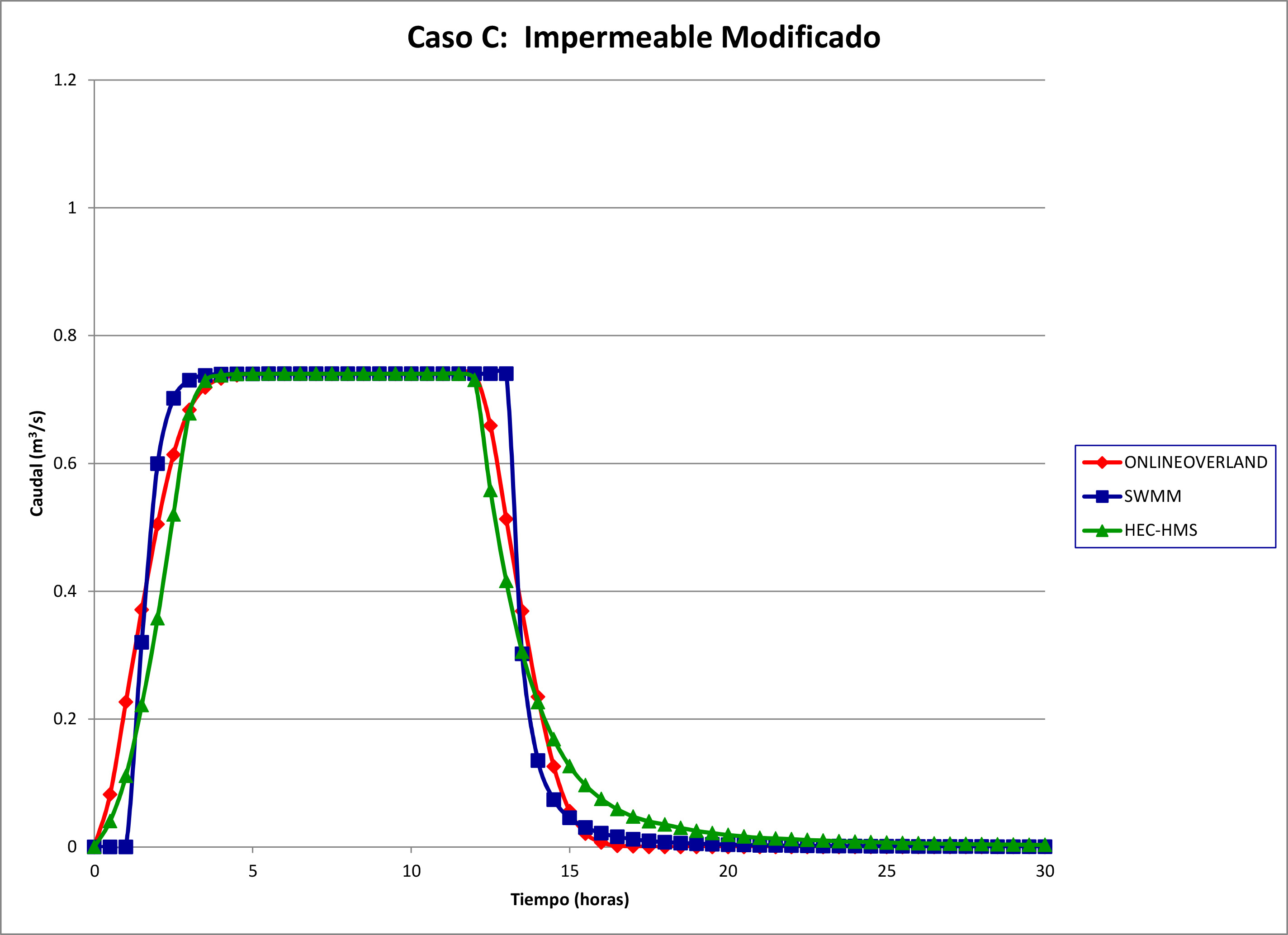
La Figura 4 muestra los hidrogramas de salida para este caso. Se elaboran las siguientes conclusiones:

  1. Caudal pico:  Los tres hidrogramas alcanzaron el caudal pico esperado, el cual, utilizando el concepto de concentración de escorrentía, es (Ponce, 2014):

    Qp = I A = (P / tr) A

    en la cual I = intensidad de precipitación total, A = área de la cuenca, P = precipitación total, and tr = duración de la tormenta. En este caso:

    Qp = (17.7666 cm / 12 hr) × 18 ha × 0.01 m/cm × 10,000 m2/ha / (3600 s/hr) = 0.740 m3/s.

  2. Duración al pico:  Los tres hidrogramas mostraron pequeñas variaciones en la duración al pico. Se hacen las siguientes observaciones:

    • ONLINEOVERLAND se comportó tal como se esperaba. El inicio de la subida del hidrograma y el inicio del receso coincidieron exactamente con el inicio y fin de la tormenta, respectivamente; véase la Fig. 4.

    • En SWMM, la subida del hidrograma mostró un desfazamiento finito y apreciable. Además, el receso del hidrograma comenzó un poco tiempo después de terminar la tormenta (tr = 12 hr); véase la Fig. 4. Cabe anotar que en este caso (impermeable), el inicio de la subida del hidrograma debe coincidir con el comienzo de la tormenta, y el inicio del receso con el fin de la tormenta.

    • HEC-HMS fue algo lento en la subida del hidrograma, por lo tanto, con el fin de conservar masa, fue también lento al final del receso; véase la Fig. 4.

  3. Conservación de la masa:   El volumen subtendido por el hidrograma es:

    V = P A

    En este caso:

    V = 17.7666 cm × 18 ha × 0.01 m/cm × 10,000 m2/ha = 31,980 m3

    Para cada modelo, el volumen del hidrograma se calculó utilizando la regla de Simpson. Los volúmenes son:

    • ONLINEOVERLAND:  31,979 m3, lo cual es 0.99997 ≅ 1.0000 del volumen esperado.

    • SWMM:  32,094 m3, es decir, un poco más del volumen esperado, con una relación 1.0036.

    • HEC-HMS:  31,809 m3, es decir, un poco menos del volumen esperado, con una relación 0.9947.

    Se concluye que sólo ONLINEOVERLAND conserva la masa exactamente, mientras que SWMM y HEC-HMS no lo hacen. Las diferencias, sin embargo, son pequeñas y pueden ser desestimables en la práctica.

Curve Number 80 Adjusted Outflow Hydrograph

Fig. 4  Caso C: Impermeable modificado.

3

RESUMEN

La Tabla 1 resume los resultados de los caudales pico calculados. Se presentan las siguientes conclusiones:

  1. Para el caso A (impermeable), los tres modelos obtuvieron el caudal pico teórico (1 m3/s).

  2. Para el caso B (permeable), sólo ONLINEOVERLAND obtuvo el caudal pico teórico (0.74 m3/s). SWMM y HEC-HMS excedieron el caudal pico teórico, debido al efecto de la simulación de abstracción inicial.

  3. Para el caso C (impermeable modificado), los tres modelos obtuvieron el caudal pico teórico (0.74 m3/s).

Tabla 1.  Caudales pico calculados.
Caso Descripción CN Precipitación efectiva (cm) Caudal pico teórico (m3/s) Caudal pico calculado (m3/s)
ONLINE OVERLAND SWMM HEC-HMS
A Impermeable 100 24.0000 1.0000 1.0000 1.0000 1.0000
B Permeable 80 17.7666 0.7400 0.7400 0.9480 0.9396
C Impermeable modificado 100 17.7666 0.7400 0.7400 0.7400 0.7400

La Tabla 2 resume los resultados de conservación de la masa. Se presentan las siguientes conclusiones:

  1. ONLINEOVERLAND conserva exactamente la masa del hidrograma.

  2. SWMM y HEC-HMS no conservan exactamente la masa del hidrograma, aunque el error no es muy significativo.

Tabla 2.  Conservación de la masa.
Caso Descripción CN Precipitación efectiva
(cm)		 Volumen real
(m3)		 Volumen calculado/Volumen real
ONLINE OVERLAND SWMM HEC-HMS
A Impermeable 100 24.0000 43,200 1.00000 1.0041 1.0024
B Permeable 80 17.7666 31,980 0.99997 1.0033 1.0028
C Impermeable modificado 100 17.7666 31,980 0.99997 1.0036 0.9947

4

CONCLUSIONES

Se han comparado tres modelos de flujo de agua superficial, ONLINEOVERLAND, SWMM, y HEC-HMS mediante corridas de prueba, especificando los mismos datos de entrada:

  1. Características de la tormenta,

  2. Características de la cuenca,

  3. Abstracciones hidrológicas, y

  4. Parámetros hidráulicos.

Se consideraron tres casos:

  • Impermeable, con CN = 100, y precipitación total P = 24 cm.

  • Permeable, con CN = 80, P = 24 cm, y, por consiguiente, precipitación efectiva Pe = 17.7666 cm (Ponce, 2010);

  • Impermeable modificado, con CN = 100, y P = 17.7666 cm.

Se obtuvieron las siguientes conclusiones:

  1. ONLINEOVERLAND se comportó adecuadamente para los tres casos (a, b, y c). Los resultados de caudal pico, duración al pico, y conservación de la masa fueron los esperados.

  2. SWMM y HEC-HMS se comportaron más o menos adecuadamente para los casos impermeables (a y c).

    Se observaron algunas inconsistencias en referencia a la duración al pico y la conservación de la masa.

    Para el caso permeable (b), el caudal pico excedió el valor teórico (Tabla 1).

    Esto se debe a que ambos modelos utilizan una abstracción inicial finita, la cual produce un aumento efectivo en el caudal pico.

Cabe mencionar que la abstracción total del método del número de la curva es válida para toda la tormenta, teniendo la abstracción inicial solamente el propósito de aumentar la abstracción total (Ponce y Hawkins, 1996; Ponce, 2000).

No está bien definido aún si la abstracción inicial debe aplicarse, en forma temporal, es decir, distribuida, a una fracción inicial de la tormenta.

La diferencias mostradas entre los hidrogramas calculados por SWMM y HEC-HMS son atribuibles a las diferentes formulaciones de los modelos, incluyendo la abstracción inicial.

Los resultados de este trabajo revelan algunas inconsistencias en la formulación de SWMM y HEC-HMS, particularmente en la duración al pico de SWMM.

Referencias bibliográficas

National Risk Management Research Laboratory. 2009. "Stormwater Management Model." Application Manual, United States Environmental Protection Agency, julio.

Ponce, V. M. 1986. Diffusion wave modeling of catchment dynamics. Journal of Hydraulic Engineering, Vol. 112, No. 8, agosto, 716-727.

Ponce, V. M., y R. H. Hawkins. 1996. Runoff curve number: Has it reached maturity? Journal of Hydrologic Engineering, Vol. 1, No. 1, enero, 11-19.

Ponce, V. M. 2000. Notas de mi conversación con Vic Mockus. Articulo en línea.
http://ponce.sdsu.edu/mockus_conversacion.html

Ponce, V. M. 2010. Onlinecurvenumber: Runoff based on NRCS runoff curve number. Online program.
http://onlinecalc.sdsu.edu/onlinecurvenumber.php

Ponce, V. M. 2014. Engineering Hydrology, Principles and Practices. Online edition, http://ponce.sdsu.edu/enghydro

U.S. Army Corps of Engineers. 2000. Hydrologic Model System HEC-HMS, Technical Reference Manual. Hydrologic Engineering Center, Davis, California.

160914 13:20