|
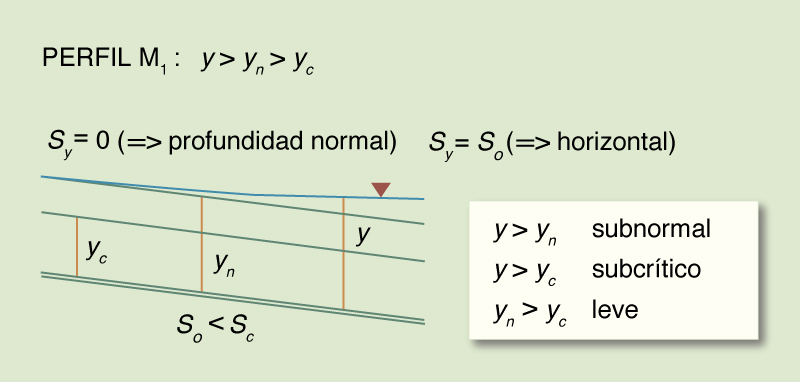
La curva de remanso M1.
Profesor de Ingeniería Civil y Ambiental
Universidad Estatal de San Diego,
California
1. INTRODUCCIÓN
Un perfil de la superficie del agua (curva de remanso) es una característica de la hidráulica
de canales la cual describe la variación de la elevación de la superficie
del agua en la dirección longitudinal
En este artículo describimos el perfil de la superficie del agua M1, un perfil subcrítico/subnormal retardado, el cual puede ser considerado el perfil más común en la práctica. El perfil M1 representa el flujo en un canal de pendiente suave, aguas arriba de un embalse (Fig. 1). Presentamos dos ejemplos y mostramos los respectivos cálculos en línea.
Fig. 1 La curva de remanso M1.
2. ECUACIÓN DE GOBIERNO
Chow (1959) ha presentado la forma clásica de la ecuación de gobierno del
flujo permanente gradualmente variado. Ponce (2015) ha propuesto una forma adimensional de esta ecuación,
basada en la pendiente crítica, como se detalla a continuación.
en la cual So = pendiente de fondo, Sc = pendiente crítica,
P = perímetro mojado,
T = ancho de la superficie,
Para (P / T ) = (Pc / Tc ), la Ec. 1 se reduce a:
Por simplicidad, el gradiente de profundidad de flujo puede escribirse de la siguiente
manera:
Substituyendo la Ec. 3 en la Ec. 2, el gradiente de profundidad de flujo es:
La Ecuación 2, o su forma reducida, la Ec. 4,
es la ecuación de flujo permanente gradualmente variado (Fig. 2).
Fig. 2 Definición de variables en el flujo en canal abierto.
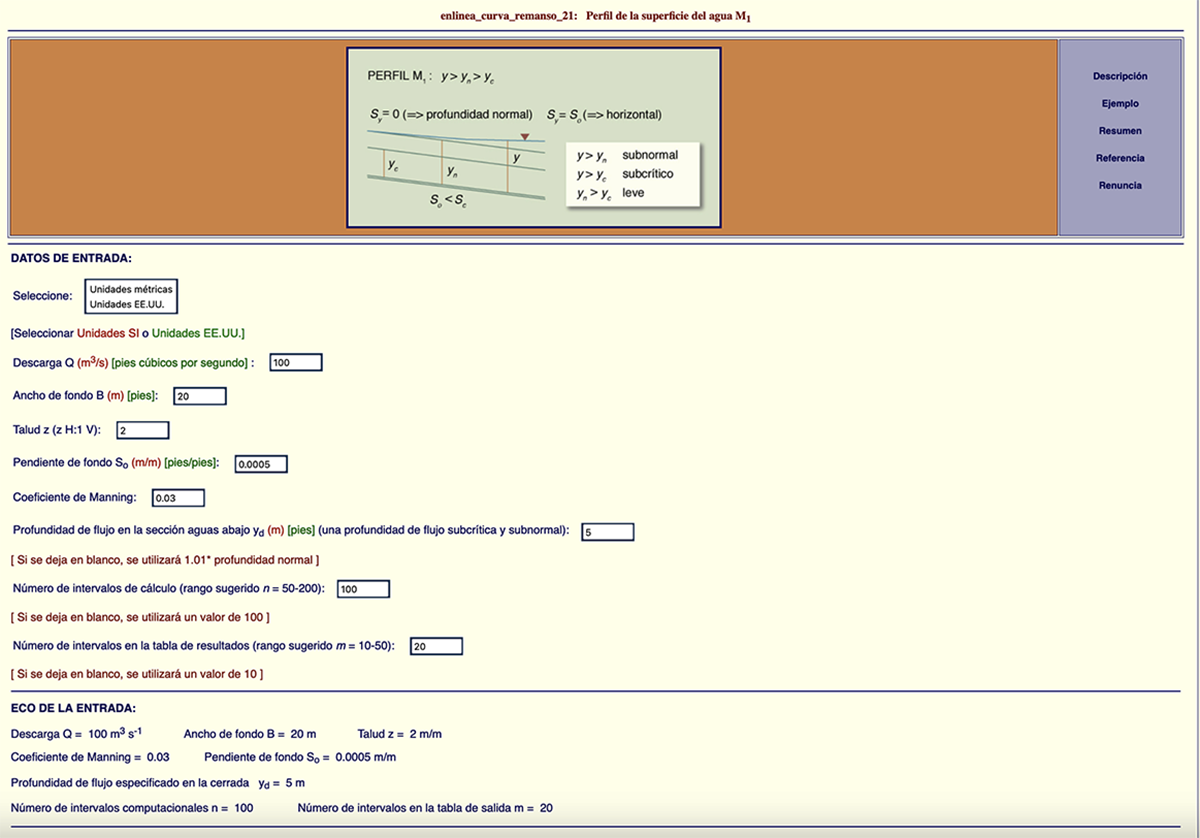
3. CÁLCULO EN LÍNEA: EJEMPLO 1
En esta sección y la siguiente (Sección 4) mostramos dos ejemplos del cálculo de una curva de remanso
M1 en un canal natural
usando la calculadora
ENLINEA_CURVA_REMANSO_21.
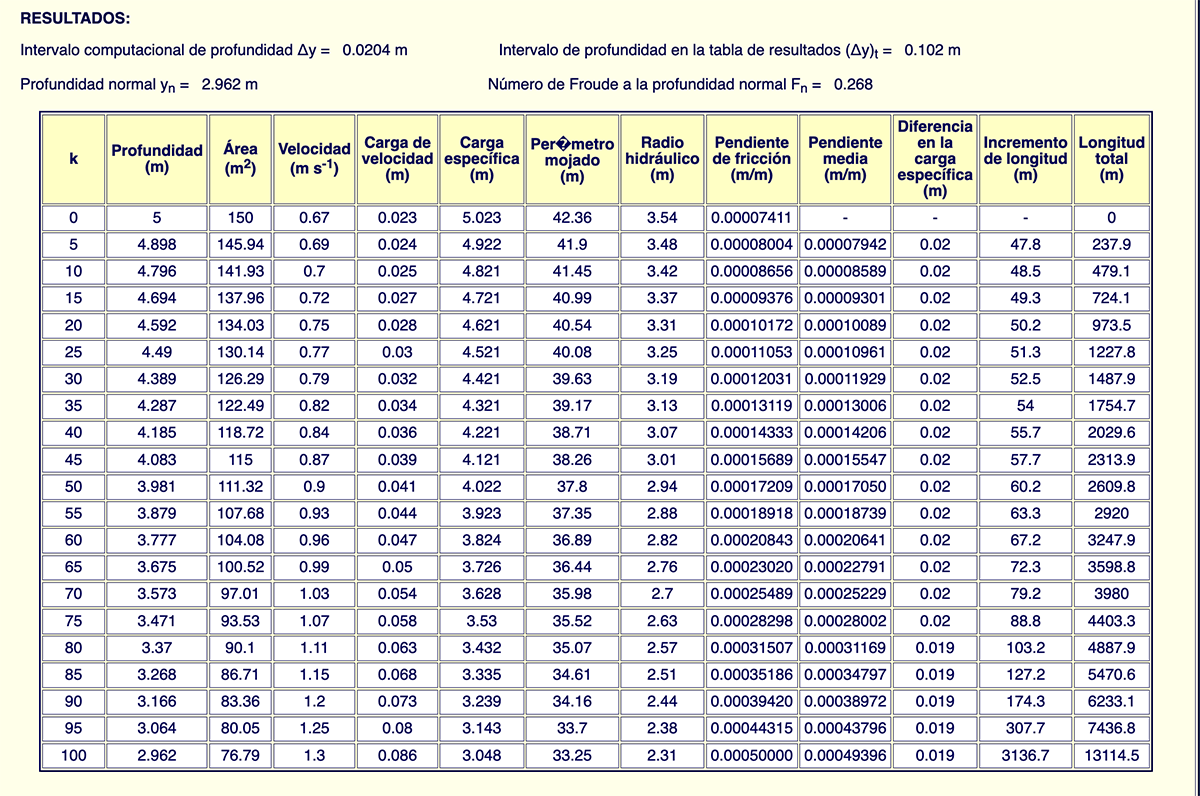
Resultados. Los resultados muestran que la profundidad de flujo en la sección
aguas abajo (yd = 5 m) disminuirá gradualmente
hasta alcanzar la profundidad normal
4. CÁLCULO EN LÍNEA: EJEMPLO 2
En esta sección mostramos el segundo ejemplo del cálculo de una curva de remanso
M1 en un canal revestido
usando la calculadora
ENLINEA_CURVA_REMANSO_21.
El siguiente cuadro muestra los datos de entrada del Ejemplo 2.
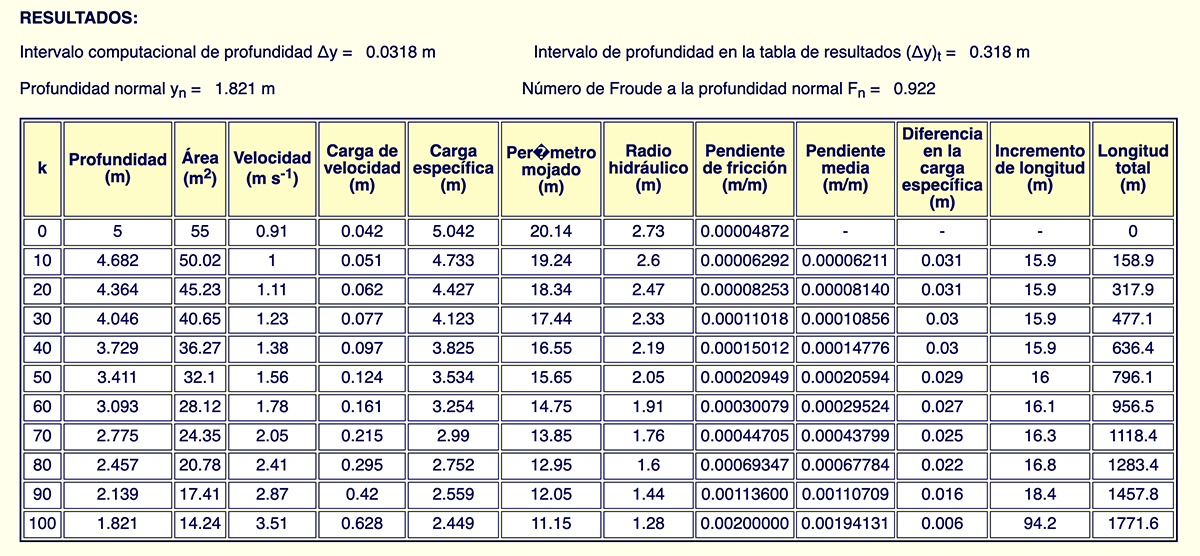
Resultados. Los resultados muestran que la profundidad de flujo en la sección
aguas abajo (yd = 5 m) disminuirá gradualmente hasta alcanzar la profundidad normal
5. RESUMEN
Se muestra en detalle un cálculo en línea de un perfil
de la superficie de agua (curva de remanso M1) de un flujo en canal abierto.
Dos ejemplos utilizando el programa
ENLINEA_CURVA_REMANSO_21
demuestran fehacientemente la utilidad de esta herramienta
para el cálculo preciso y efectivo de un perfil de la superficie del agua M1.
BIBLIOGRAFÍA
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, Inc, New York, NY.
Ponce, V. M. 2015.
Fundamentos de la Hidráulica de Canales.
Libro de texto. https://ponce.sdsu.edu/canales/index.html
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 231211 |