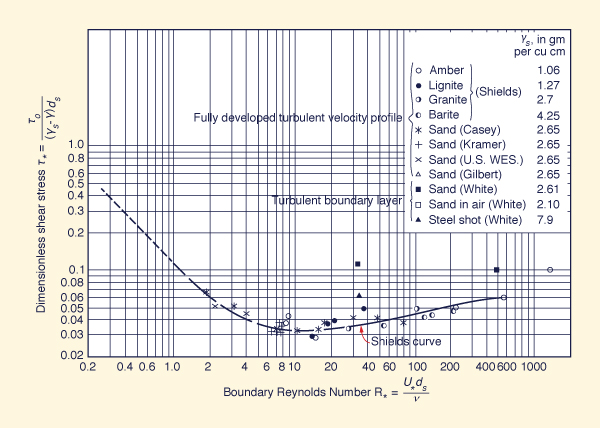
1 - INTRODUÇÃO O conceito de início do movimento para o fluxo em canal de leito de areia foi introduzido por Shields (Sociedade Americana de Engenheiros Civis, 1975; p. 96). A curva Shields é o limiar no qual as partículas de sedimento de material de leito começam a se mover (Fig. 1). Esse limiar é importante no projeto de canais para garantir o movimento dos sedimentos e evitar o entupimento. Neste artigo, considera-se o critério de Shields em termos do número de Froude e da velocidade média necessária para o início do movimento em canal de leito de areia. Para aprimorar o entendimento, foi desenvolvido um algoritmo iterativo online para calcular esses valores.
2 - CRITÉRIO DE SHIELDS
O critério Shields para início de movimento relaciona a tensão de
cisalhamento adimensional
τ* com o número de número limite R*
como mostrado na Figura 1. Acima de curva tem-se movimento,
abaixo da curva o movimento não está presente. O critério Shields é:
em que τo = tensão de cisalhamento do fundo,
γs = peso específico das partículas de sedimento,
3 - CRITÉRIO DE FROUDE O número de Froude é:
em que V = velocidade média, D = profundidade hidráulica e g = aceleração gravitacional. A equação quadrática do atrito causado pelo fluxo em canal aberto é (Ponce, 2014):
em que ρ = densidade de massa de água, e f = fator de atrito, igual a 1/8 do fator de atrito de Darcy-Weisbach fD. Substituindo Eqs. 2 e 3 em 1:
Na maioria dos casos de interesse prático, a razão γs /γ é igual a 2,65. Neste caso, o número de Froude para início de movimento é:
Como uma primeira aproximação, a curva Shields sugere um valor crítico aproximadamente constante de tensão de cisalhamento adimensional τ*c = 0,04, aplicável para uma ampla gama de números de Reynolds (Fig. 1). Portanto, a Eq. 5 reduz para:
O fator de atrito varia normalmente na faixa 0,002 ≤ f ≤ 0,005, o que corresponde aos fatores de atrito de Darcy-Weisbach 0,016 ≤ f D ≤ 0,040. Para ilustrar, assumimos um valor médio f = 0,0035. Portanto, o critério de Froude aplicável é:
Para um determinado diâmetro de partícula, relacionado à profundidade hidráulica, a Eq. 7 indica o número de Froude que deve ser excedido para assegurar o início do movimento. Por exemplo, para ds = 0,4 mm e profundidade hidráulica D = 1 m, isto é, ds / D = 0,0004, Eq. 7 reduz para:
Combinando Eqs. 2 e 6, a velocidade média relacionada é:
Portanto:
4 - APLICAÇÃO COM COEFICIENTE DE MANNING n
A relação entre o fator de atrito f e o coeficiente de Manning n é (Ponce, 2014):
em que g = aceleração gravitacional, n = coeficiente de Manning, R = raio hidráulico e K = 1 em
unidades SI e 1,486 em unidades dos EUA.
Para um canal hidraulicamente largo: R ≅ D. Substituindo a Eq. 10 na Eq. 6, a expressão para
o número de Froude nas unidades do SI é:
Por exemplo, dado: D = 1 m, ds = 0,4 mm = 0,0004 m, e n = 0,019:
Considerando-se as unidades dos EUA, a expressão para o número de Froude é:
0,067 D 1/6 (ds / D )1/2
onde D e ds são dados em pés.
Por exemplo, dado: D = 3,28 pés, ds = 0,4 mm = 0,001312 pés, e n = 0.019:
5 - ALGORITMO ITERATIVO
Um cálculo mais preciso do número de Froude e da velocidade média relacionada pode ser
obtido usando (Eq. 5) uma tensão de cisalhamento crítica adimensional obtida pela curva Shields real, em vez do valor constante assumido de 0,04. Esse procedimento, no entanto, requer uma
iteração. O algoritmo a seguir é sugerido.
Assuma um valor de R*
Use a Fig. 1 para encontrar
τ*c
Usando a Eq. 1, calcule τo
Calcular o novo valor de R* = (U* ds / ν), no cual ν =
viscosidade cinemãtica, função da temperatura.
Pare
se o novo valor de R* estiver próximo ao assumido na Etapa 1 (dentro de uma tolerância pequena) e use o último valor de τ*c (calculado na Etapa 2) na Eq. 5;
Caso contrário, retorne à Etapa 1 e use o novo valor de R* (calculado na Etapa 5) como o
valor assumido e continue a iteração.
Exemplo.
Considerando-se os seguintes dados de um canal: diâmetro de partícula ds = 0,4 mm,
profundidade hidráulica D = 1 m, fator de atrito Darcy-Weisbach adimensional f = 0,0035
e temperatura da água
CALCULO ONLINE. Usando o algoritmo iterativo incorporado em EMLINHA SHIELDS VELOCIDADE,
o número de Froude é F = 0,081 e a velocidade média V
= 0,25 m/s. Observe que esses resultados são um pouco mais precisos do que os obtidos no
cálculo direto aproximado usando Eqs. 6 e 9.
6 - RESUMO
O critério clássico de engenharia de sedimentação é expresso em termos do número de
Froude e da velocidade média relacionada necessária para o início do movimento em um canal de
leito de areia. Para resolver o problema de forma exata, um algoritmo iterativo é implementado na calculadora
EMLINHASHIELDSVELOCIDADE:
http://onlinecalc.sdsu.edu/emlinhahieldsvelocidade.php
7 - REFERENCIAS
American Society of Civil Engineers. 1975. Sedimentation Engineering.
ASCE Manuals and Reports on Engineering Practice No. 54.
Ponce, V. M. 2014.
Fundamentals of open-channel hydraulics.
Online textbook.
|
| 180905 11:00 |