ONDAS CINEMÁTICAS Y DINÁMICAS: LA DECLARACIÓN DEFINITIVA
Profesor Emérito de Ingeniería Civil y Ambiental Universidad Estatal de San Diego, California
1. INTRODUCCIÓN Este artículo contrasta las ondas cinemáticas y dinámicas en el flujo en canal abierto. El objetivo es comprender estos conceptos a fondo, para facilitar su uso más amplio en la práctica de la ingeniería hidráulica. Las ondas cinemáticas y dinámicas se encuentran cada una en uno de los extremos de la escala de ondas, es decir, el espectro de números de onda adimensional. Las ondas cinemáticas están en el lado izquierdo (valor pequeño) y las ondas dinámicas en el lado derecho (valor grande). Tomados por sí solos, estos dos conceptos son mutuamente excluyentes; una onda es cinemática o es dinámica. Hacia la mitad de la escala, una onda que no es ni cinemática ni dinámica puede interpretarse como una onda cinemático-dinámica mixta, a falta de un mejor término. La celeridad variable hace que estas ondas sean difusivas, desde ligeramente hasta extremadamente difusivas.
2. ESCALA DE ONDAS
La "escala" de la onda es lo que determina si una onda es cinemática o dinámica. En este contexto, "escala" no se refiere al valor absoluto del número de onda, definido de otra manera como σ = 2π /L,
sino más bien a su valor relativo, o número de onda adimensional,
definido como σ* = 2π (Lo /L).
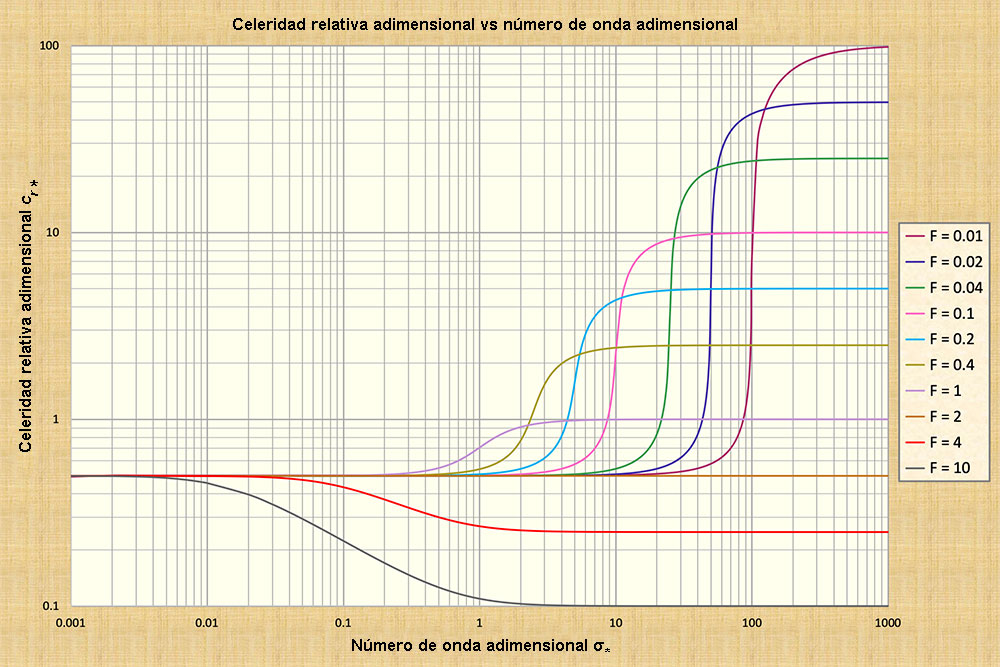
El efecto del número de onda adimensional es reducir sustancialmente el número de órdenes de magnitud necesarios para el análisis. En efecto, la Fig. 2 muestra la variación de las celeridades de ondas relativas adimensionales
cr* graficadas en sólo seis (6) órdenes de magnitud de números de ondas adimensionales
3. ONDAS CINEMÁTICAS
La Figura 1 muestra la gráfica de las celeridades de onda relativas adimensionales a lo largo del espectro de números de onda adimensionales, desde muy pequeñas, correspondientes a ondas cinemáticas
(σ* = 0.001), hasta muy grandes, correspondientes a ondas dinámicas
Nótese que a lo largo del espectro de números de ondas adimensionales σ*,
la celeridad de onda relativa adimensional
cr*
es una constante e igual a cr* = 0.5 sólo para el número de Froude F = 2. Notamos específicamente que esta condición de flujo corresponde a la fricción de Chezy en un canal hidráulicamente ancho (véase Cuadro B abajo)
(Ponce y Simons, 1977). Ésta es la condición física para la cual todas las escalas de onda viajan con la misma celeridad, lo que representa el inicio de la estabilidad/inestabilidad del flujo: estabilidad para F < 2, e inestabilidad F > 2.
Un examen más detallado de la Fig. 1 revela que las ondas cinemáticas están posicionadas a la izquierda de la figura, de manera asintótica al valor constante cr* = 0.5 en el extremo izquierdo de la figura, la cual corresponde a la celeridad relativa adimensional de la onda cinemática para la fricción de Chezy en un canal hidráulicamente ancho ( Ponce, 2014). El concepto de celeridad de onda cinemática, que es similar al de celeridad de onda de inundación, se debe a Seddon (1900), quien fue el primero en derivar la fórmula que lleva su nombre. En el siguiente recuadro se incluyen expresiones relacionadas.
Reiteramos que las ondas cinemáticas existen, aunque admitámoslo sólo como una aproximación conveniente, típicamente en el lado izquierdo del espectro adimensional de números de onda. Corresponden a una gran clase de ondas de inundación, particularmente aquéllas que están sujetas a muy poca (o, de lo contrario, insignificante) atenuación. También pueden aparecer en el modelado de flujo sobre el terreno, en el cual las pendientes de fondo predominantes son lo suficientemente grandes como para propiciar una condición de flujo cinemático y las ondas cinemáticas resultantes (Woolhiser y Liggett, 1967). El trabajo de
Seddon (1900), seguido por el de
4. ONDAS DINÁMICAS
Las ondas dinámicas se encuentran a la derecha del espectro de números de onda adimensionales,
La Figura 1 muestra los valores de las celeridades de onda dinámicas relativas adimensionales cdrd que se encuentran a la derecha. Por ejemplo, utilizando la última definición de Hemos demostrado que la Fig. 1 representa correctamente los valores de las celeridades dinámicas relativas adimensionales o de Lagrange, Por lo tanto, demostramos que la Fig. 1 abarca tanto las ondas cinemáticas como las dinámicas, es decir, las ondas dinámicas se encuentran a la derecha del número de onda adimensional σ*. En este lugar, las celeridades de onda dinámicas relativas adimensionales son una función del número de Froude del flujo de equilibrio. Según Ponce y Simons (1977), la atenuación de una onda dinámica es cero, es decir, las ondas dinámicas no están sujetas a disipación, al menos en un análisis unidimensional. Esta conclusión se desprende directamente de la Fig. 1, porque en el rango dinámico aplicable, hacia el extremo derecho de la figura, se muestra que la celeridad de la onda es constante y, por lo tanto, independiente de la escala. Esta conclusión confirma que una onda dinámica no está sujeta a atenuación. Entonces, una onda dinámica es una onda superficial comparativamente pequeña, la cual presenta un número de onda adimensional correspondientemente grande, la cual viaja a una celeridad relativa adimensional que es el recíproco del número de Froude del flujo de equilibrio, y no está sujeta a atenuación. Las ondas dinámicas existen, aunque sólo como una aproximación conveniente, por lo general en el lado derecho del espectro de número de onda adimensional. Corresponden a una clase de ondas superficiales relativamente cortas, en particular aquéllas que están sujetas a una atenuación muy pequeña o insignificante.
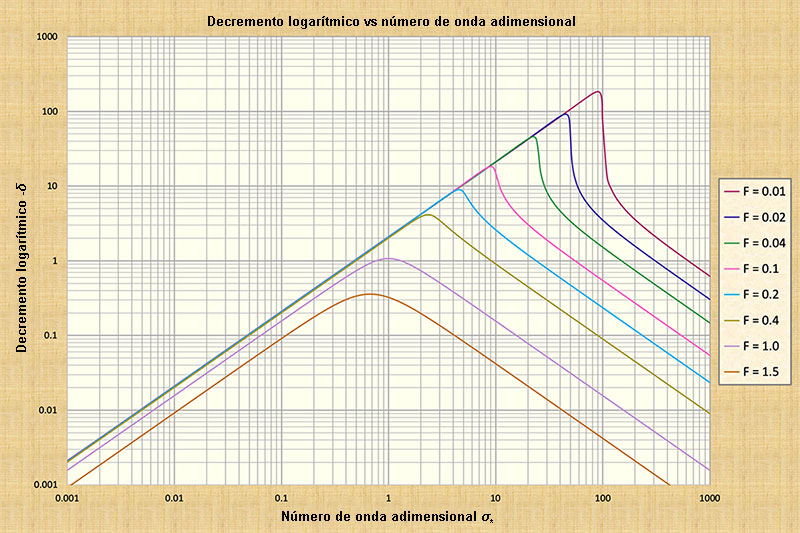
5. ONDAS CINEMÁTICO-DINÁMICAS MIXTAS Las ondas cinemáticas se encuentran a la izquierda del espectro de números de onda adimensional, mientras que las ondas dinámicas se encuentran a la derecha; ninguna de ellas esté sujeta a atenuación. Esto se debe a la constancia de las respectivas celeridades dentro del rango de análisis especificado. La atenuación de las ondas se debe a la variación de la celeridad de grupo, que alcanza un valor máximo, dependiendo del número de Froude, hacia (la derecha de) los números de onda adimensionales de rango medio. Cuanto mayor sea la variabilidad de la celeridad (con el número de onda adimensional), mayor será la atenuación de la onda, que se muestra que aumenta con los números de Froude; ver Fig. 1 y 2. La atenuación de las ondas alcanza un pico en un valor de número de onda adimensional σ* correspondiente al punto de inflexión en la curva celeridad-número de onda.
Concluimos que hacia la mitad del espectro de número de onda adimensional, la atenuación de onda es máxima, mientras que hacia los extremos, tanto izquierdo como derecho, es mínima (Fig. 2).
Por lo tanto, las ondas cinemático-dinámicas mixtas están sujetas a una atenuación variable, desde leve a muy fuerte, y la cantidad de atenuación varía con el valor del número de onda adimensional, en relación con la ubicación del punto de inflexión en la curva de celeridad-número de onda. En ciertos casos, la onda cinemática-dinámica mixta puede ser tan fuertemente disipativa que desafíe por completo el cálculo. Esta situación fue admirablemente descrita por Lighthill y Whitham (1955) en su tratado seminal sobre las ondas cinemáticas:
Para finalizar, queremos señalar que nuestras "ondas cinemático-dinámicas mixtas" han sido, durante los últimos 50 años, simplemente denominadas "ondas dinámicas", lo cual ha contribuido a la confusión semántica (Fread, 1985).
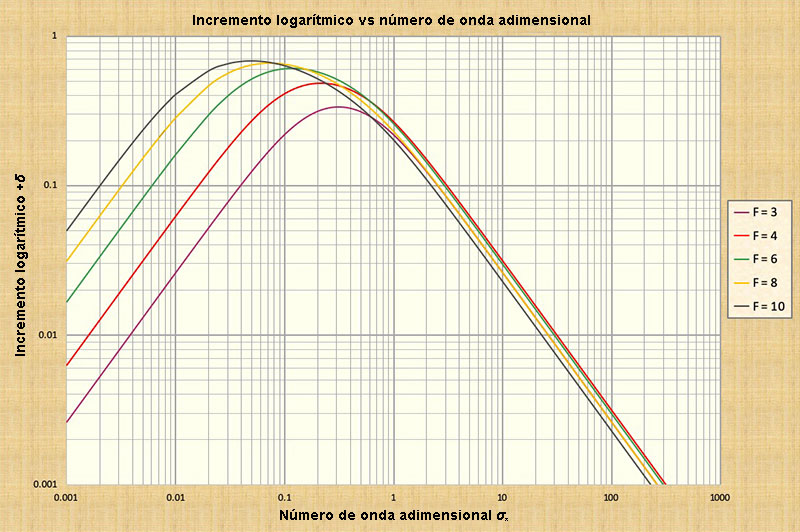
6. ONDAS DE DIFUSIÓN
Habiendo establecido de manera concluyente que ni las ondas cinemáticas ni las dinámicas se atenúan, y por el contrario, que las ondas cinemático-dinámicas mixtas podrían estar sujetas a una atenuación muy fuerte, presentamos aquí otro tipo de onda intermedia, que, dependiendo del valor del número de onda adimensional, se encuentra entre las ondas cinemáticas y las ondas
Concluimos que la difusión de onda se produce por: (1) la interacción del término de gradiente de presiones con los términos de fricción y gravedad, como en la onda de difusión; o (2) por la interacción de todos los (cuatro) términos en la ecuación de movimiento, es decir, como en la onda
La difusión de la onda de difusión se describe por el decremento logarítmico δ =
- 2 π (σ* / 3),
que es aplicable sólo dentro del rango de números de onda adimensionales en el cual la onda de difusión es predominante, es decir, dentro de un rango estrecho entre el de las ondas cinemáticas
Las ondas de difusión resultan ser más comunes que las ondas cinemáticas o las ondas
7. RESUMEN Se analizan y comparan varios tipos de ondas en aguas someras en el flujo en canales abiertos en relación con su celeridad y propiedades de atenuación. Estas ondas son: (1) ondas cinemáticas, Las ondas cinemáticas se propagan con una celeridad constante y no son difusivas. La celeridad constante de las ondas cinemáticas se conoce en la literatura de tránsito de inundaciones como "celeridad de Seddon". Las ondas dinámicas se propagan con una celeridad constante y no son difusivas. La celeridad constante de las ondas dinámicas se denomina "celeridad de Lagrange" y se aplica a las ondas "cortas" en el flujo en canal abierto. Las ondas cinemático-dinámicas mixtas se propagan con una celeridad que varía con el número de onda adimensional, y esta propiedad les confiere la capacidad de difusionarse, es decir, de atenuarse o disiparse. En ciertos casos, estas ondas cinemático-dinámicas mixtas pueden ser tan fuertemente disipativas que desafien por completo el cálculo.
Las ondas de difusión se encuentran en un punto intermedio entre las ondas cinemáticas y las ondas cinemático-dinámicas mixtas, en términos de escala relativa. Estas ondas se propagan aproximadamente con la celeridad de Seddon y se ha demostrado que son ligeramente difusivas;
BIBLIOGRAFíA Fread, D. L. 1985. "Channel Routing," in Hydrological Forecasting, M. G. yerson y T. P. Burt, eds. New York: John Wiley. Ponce, V. M. y D. B. Simons. 1977. Shallow wave propagation in open channel flow. Journal of Hydraulic Engineering, ASCE, 103(12), 1461-1476. Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July. Ponce, V. M. 2014. Fundamentals of Open-channel Hydraulics. Online text. Seddon, J. A. 1900. River hydraulics. Transactions, ASCE, Vol. XLIII, 179-243, June.
Woolhiser, D. A. y J. A. Liggett. 1967.
Unsteady one-dimensional flow over a plane: The rising hydrograph.
|
| 250202 |