Propriedades geométricas
de uma seção parabólica


Jhonath W. Mejía e Víctor M. Ponce

210223

ABSTRATO

O objetivo deste artigo é formular as equações para o cálculo das propriedades geométricas de uma seção parabólica, em a hidráulica de canais. Essas equações são comparadas com as apresentadas no capítulo 2 do livro de Ven Te Chow (em Espanhol) "Hidráulica de Canaless Abiertos" (1994).

1.  INTRODUÇÃO

O cálculo das propriedades geométricas de uma seção de canal parabólico é feito através da aplicação de integrais normais e de linha, usando os parâmetros que caracterizam uma parábola.

2.  PROPRIEDADES GEOMÉTRICAS DE UMA SEÇÃO PARABÓLICA

A equação de Manning é:

             A
  Q  =  ____  R 2/3  So1/2
             n 		(1)

em que Q = vazão A = área de fluxo; R = raio hidráulico; So = inclinação do fundo; e n = rugosidad de Manning. Portanto:

   Q n              A 2/3
  _____  =  A  _____
  So1/2            P 2/3 		(2)

em que o fator de seção Fs é dado da seguinte forma:

              A 5/3
  Fs  =  ______
             P 2/3 		(3)

Portanto:

               A 5
  Fs3  =  _____
               P 2 		(4)

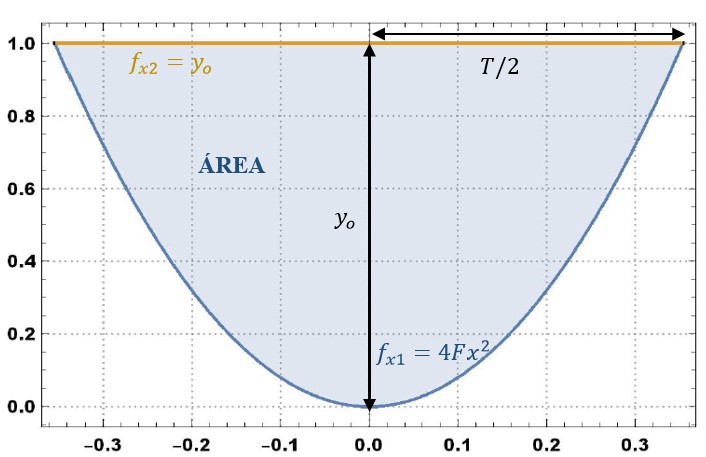
A área e o perímetro de uma seção parabólica para uma profundidade da água yo e largura de superfície livre T são mostrados na Fig. 1.

Fig. 1 Diagrama de definição de uma seção parabólica.

Para calcular a área, o seguinte integral é usado:

                    T/2
  A  =  2 ∫  (fx2 - fx1) dx
                   0 		(5)

                    T/2                          T/2
  A  =  2 ∫  (yo) dx  -  2 ∫  (4Fx 2) dx
                   0                              0 		(6)

                                          x 3
  A  =  2yo [ x ] 0T/2  -  8F [ ___ ] 0T/2
                                          3 		(7)

                      FT 3
  A  =  yoT -  _____
                       3 		(8)

em que 4F é um parâmetro definido como segue:

               yo            4yo
  4F  =  ______  =  _____
            (T/2) 2        T 2 		(9)

Portanto:

             yo
  F  =  _____
            T 2 		(10)

Substituindo a Eq. 10 na Eq. 8:

                         yo       T 3                    yoT
  A  =  yoT  -   _____  _____  =  yoT  -  _____
                        T 2       3                       3 		(11)

Portanto:

            2yoT
  A  =  ______
               3 		(12)

Para o perímetro molhado, uma integral de linha é usada:

                    T/2
  P  =  2 ∫  [1 + (f 'x1) 2] 1/2 dx
                   0 		(13)

                    T/2
  P  =  2 ∫  [1 + (8F) 2x 2] 1/2 dx
                   0 		(14)

A Equação 14 está na forma de uma integral conhecida:  ∫ (a2+x2)1/2dx, e sua solução é:

                 x                                  senh-1 (8Fx)
  P  =  2 [ ___ [1 + (8F) 2x 2] 1/2 + _______________ ] 0T/2
                 2                                        2 (8F) 		(15)

                  T/2                                         senh-1 (8FT/2)
  P  =  2 { ______ [1 + (8F)2(T/2) 2] 1/2 + _________________ }
                    2                                                  2(8F) 		(16)

Substituindo a Eq. 10 na Eq. 16, obtemos:

                  T/2                                                   senh-1 (8(yo/T 2)(T/2))
  P  =  2 { ______ [1 + (8(yo/T 2)) 2 (T/2) 2] 1/2 + ________________________ }
                    2                                                            2(8(yo/T 2)) 		(17)

             T            16yo 2              T 2                   4yo
  P  =  ____ ( 1 + ______ ) 1/2 + ______ senh-1 ( ______ )
             2              T 2                8yo                    T 		(18)

             T                  4yo                     T                     4yo
  P  =  ____ [ ( 1 + ( ______ ) 2 ) 1/2 + ______ senh-1 ( ______ ) ]
             2                   T                      4yo                    T 		(19)

A Equação 19 pode ser expressa como uma função de logaritmos, usando a seguinte fórmula:

 senh-1θ = ln [θ+ (1+θ 2) 1/2] (20)

Portanto:

             T                  4yo                   T            4yo                  4yo
  P  =  _____ { [1 + ( _____ ) 2 ] 1/2 + _____ ln [ _____ + ( 1 + ( _____ ) 2 ) 1/2] }
             2                   T                    4yo           T                     T 		(21)

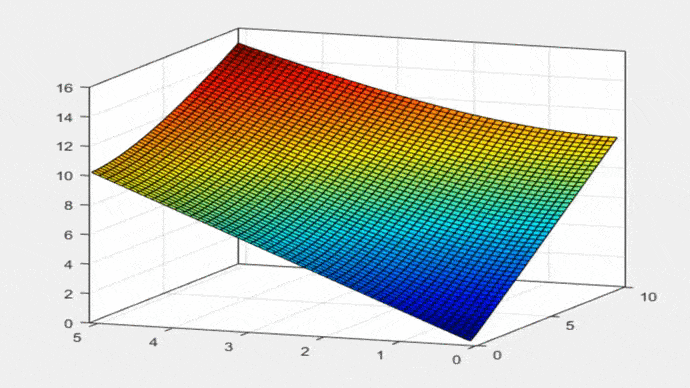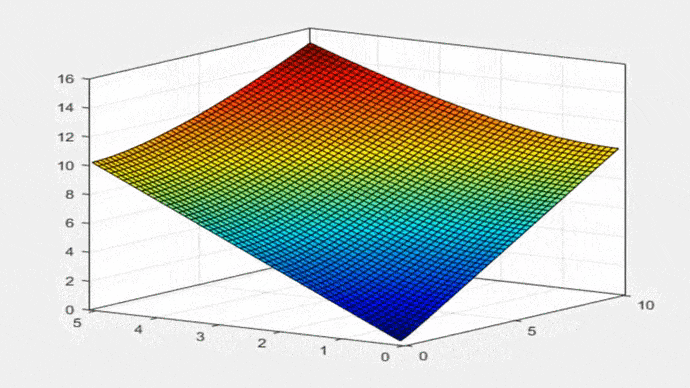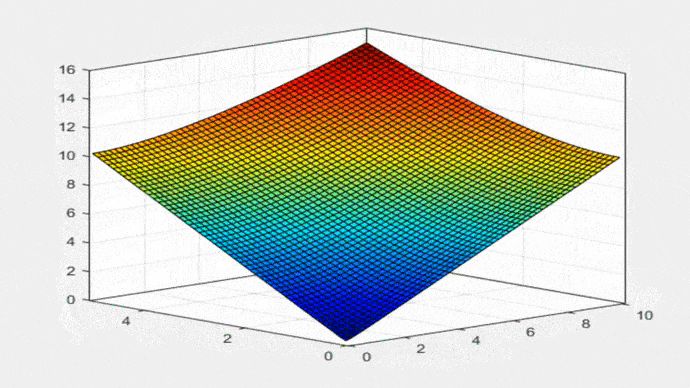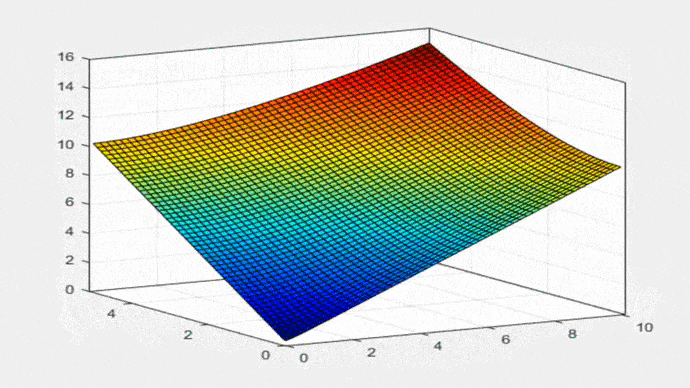
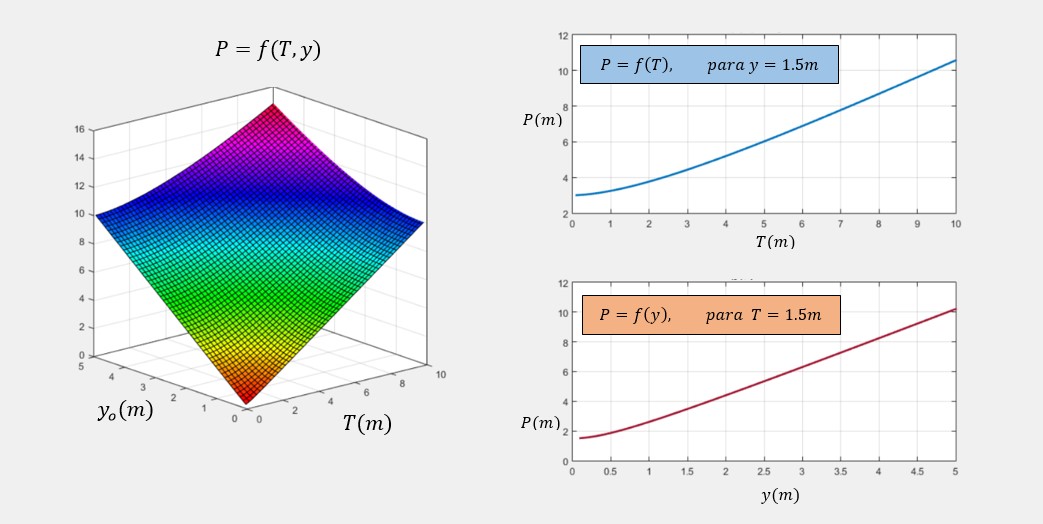
A Equação 21 é a mesma fórmula que aparece na Tabela 2-1 do livro de Ven Te Chow (1994): “Hidráulica de canais Abertos”.

A Figura 2 mostra a Equação 19 em forma gráfica: P = f (T,yo), para 0 < T < 10; 0 < yo < 5:

Fig. 2  Perímetro molhado versus largura da superfície livre e profundidade da água.

A Eq. 19 é usada para construir as propriedades geométricas da parábola.

Largura da superfície livre T é:

            3A
  T  =  _____
            2yo 		(22)

Raio hidráulico R é:

             A
  R  =  _____
             P 		(23)

                                                  2yoT
                                                ______
                                                     3
  R  =  ____________________________________________________
             T                  4yo                    T                     4yo
           ____ { [ 1 + ( ______ ) 2 ] 1/2 + ______ senh-1 ( ______ ) }
             2                   T                      4yo                   T 		(24)

            4yo                 4yo                     T                    4yo
  R  =  _____ { [ 1 + ( ______ ) 2 ] 1/2 + ______ senh-1 ( ______ ) } -1
              3                    T                      4yo                    T 		(25)
é

Profundidade da água D é:

             A          A
  D  =  ____  =  ____
             T         3A
                       ____
                        2yo 		(26)

Portanto:

            2yo
  D  =  _____
              3 		(27)

A Tabela 1 resume as propriedades de uma seção parabólica.

Tabela 1.   Propriedades geométricas de uma seção parabólica.
Propriedade Equação Fórmula
Área de fluxo Eq. 12           2yoT
  A  =  ______
           3
Perímetro molhado Eq. 19      T                  4yo                     T                     4yo
  P  =  ____ { [ 1 + ( ______ ) 2 ] 1/2 + ______ senh-1 ( ______ ) }
   2                   T                      4yo                    T
Largura
da
superfície
livre		 Eq. 22            3A
  T  =  ______
            2yo
Raio
hidráulico		 Eq. 25    4yo                  4yo                    T                    4yo
  R  =  _____ { [ 1 + ( ______ ) 2 ] 1/2 + ______ senh-1 ( _____ ) } -1
  3                    T                      4yo                   T
Profundidade hidráulica Eq. 27            2yo
  D  =  ______
            3

APÊNDICE I.   BIBLIOGRAFIA

Chow, V. T. 1994. Hidráulica de Canales Abiertos, McGraw-Hill Interamericana, Bogotá, Colombia.

Leithold, L. 1998. El Cálculo, Séptima Edición, Oxford University Press - Harla México, S.A.

APÊNDICE II.   NOTAÇÃO

Os seguintes símbolos são usados neste documento:

Q = vazão;

n = coeficiente de Manning;

So = inclinação do fundo;

yo = profundidade da água;

Fs = fator de seção;

A = área de fluxo;

P = perímetro molhado;

T = largura da superfície livre;

R = raio hidráulico; e

D = profundidade hidráulica.

210223 10:10

Los Os documentos em Portable Document Format (PDF) requerer Adobe Acrobat Reader 5.0 para ver; descargar Adobe Acrobat Reader.