1.  INTRODUCTION

A rating curve is a fundamental tool in hydraulic and hydrologic engineering. The curve depicts the relationship between discharge and stage at a given point in a stream, river, channel, canal, or free-surface conduit. Under steady uniform flow, the rating is unique, i.e., there is one value of discharge for each value of stage. The situation, however, is complicated under unsteady flow conditions. Depending on the flow, the rating may actually be nonunique, typically showing a histeresis, or looped rating, i.e., a nonsingular value of discharge as a function of stage, and vice versa.

Further complications arise if the flow is actually able to move its bed, as it is typically the case in alluvial channels and/or rivers in the absence of geologic controls such as rock outcrops. In medium-sized to large rivers, the flow acts to minimize the changes in stage, effectively reducing the stage variability between low flows and high flows (Kennedy, 1983). Nature accomplishes this feat by increasing form friction during low flows (by means of the development of bedforms, such as ripples and dunes), and by obliterating the bedforms during high flows, reducing form friction to negligible amounts, leaving grain friction as the only acting type of friction.

Furthermore, unsteady, or nonequilibrium, sediment transport may also cause alterations or modifications in (previously established) rating curves. Rivers are typically subjecting their boundaries to recurring cycles of erosion and deposition, depending on neighboring natural phenomena and/or anthropogenic activities. Some active rivers may be aggrading; yet, others may be degrading. Very active rivers may substantially change their cross section and/or course/alignment during major floods. Invariably, shifts in rating are the net result of these geomorphic processes.

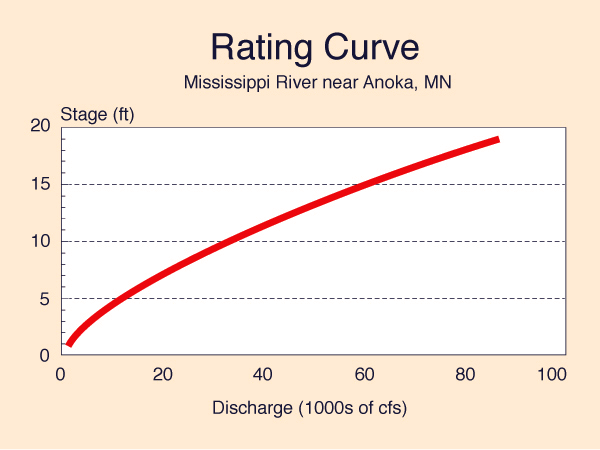
2.  STEADY UNIFORM FLOW RATING

The steady uniform flow rating or equilibrium rating is a unique relationship between discharge and stage at a given station (Fig. 2). The curve is developed by the simultaneous measurement of discharge and stage at a given gaging station, and by subsequently fitting a curve to the measured data. For increased accuracy, the site location must be free from the following conditions: (1) backwater effects, (2) unsteady flow features (waves), and/or (3) other irregularities that would tend to mask the reproducibility of the singled-valued rating.

Fig. 2   Rating curve for the Mississippi river at Anoka, Minnesota.

In engineering practice, the rating curve is used together with a staff gage (Fig. 3). The latter measures water surface elevation, and this value is entered to the rating curve in order to obtain the discharge of interest. Note that modern digital recorders with electronic data-transfer capabilities are becoming increasingly available for measurement automation.

Fig. 3   Typical staff gage.

The permanence of the rating is normally subject to verification by periodic stage-discharge measurements. The frecuency of the verification process will depend on whether the gaging site of interest is optimal when all relevant hydraulic factors are considered.

---

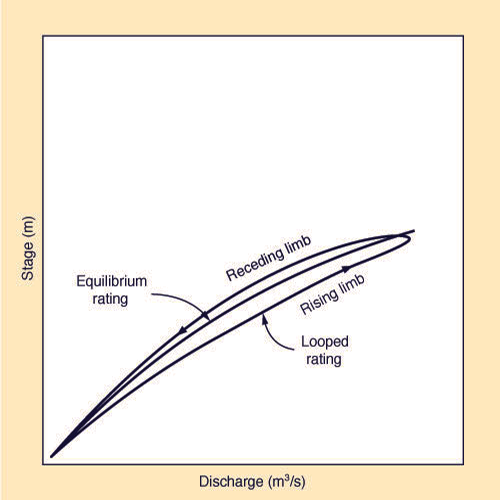
3.  UNSTEADY FLOW RATING

The unsteady flow or non-equilibrium flow rating is a graph showing a hysteresis in the rating, whereupon the actual rating curve (Fig. 4) loops around the established equilibrium rating. The shape of the loop depends largely on the extent of the flow unsteadiness; the wider the loop, the greater the unsteadiness. The typical loop is such that the rising limb (of the flood hydrograph) corresponds to greater discharges for a given stage, while the receding limb corresponds to smaller discharges (Fig. 4). Note that if the flood wave is a kinematic wave, the rating curve will coalesce into the equilibrium rating (Section 2) and the loop will disappear (Ponce and Simons, 1977). Conversely, if the flood wave is a diffusion wave, the loop remains noticeable and, therefore, measurable. In fact, theory asserts that the existence of a looped rating is a clear indication of flood wave diffusion. Loops in rating curves may be calculated with the help of digital models of unsteady open-channel flow.

Fig. 4   A looped rating curve.

---

4.  SHORT-TERM SEDIMENTATION EFFECTS

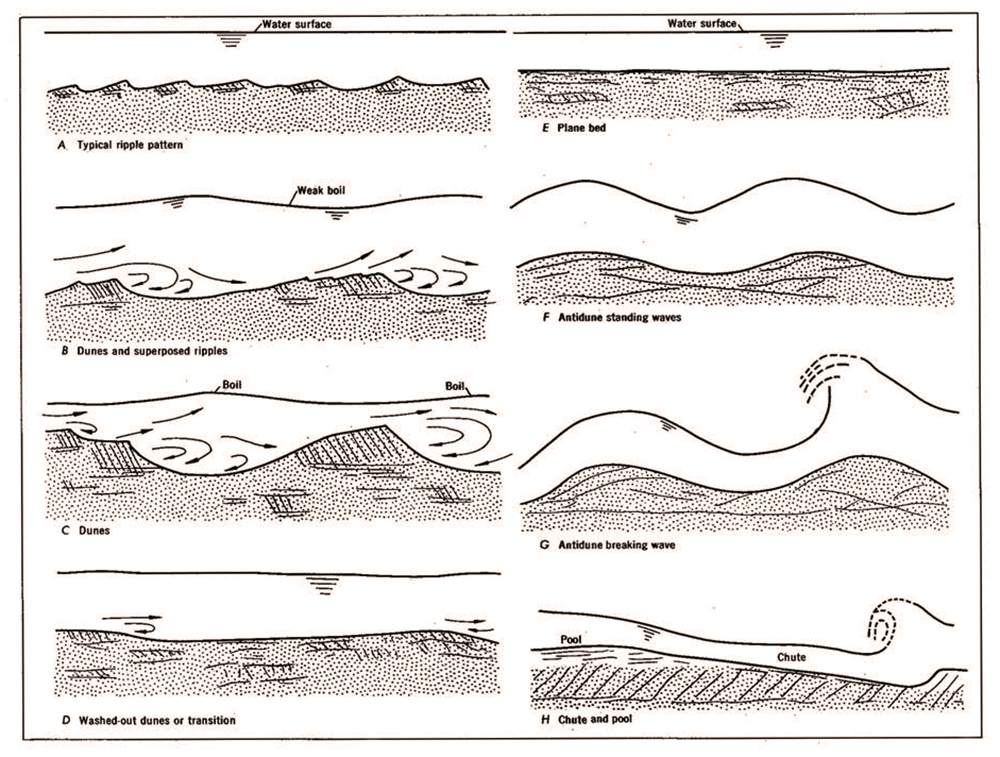
The short-term sedimentation effect arises in situations where the bottom shear stress produced by the flow (due to the no-slip condition at the channel boundary) is able to move its bed freely. This is typically the case of alluvial channels/rivers, wherein the bottom consists mostly of sand and silt particles. Under lower regime, with Froude numbers F < 0.5, the bottom shear will produce first, ripples, and then, dunes, effectively increasing the total friction, consisting of grain and form friction, the latter due to the bedforms. Under upper regime, with Froude numbers F ≥ 0.5, the comparatively large momentum of the flow will act to obliterate the lower regime bedforms (ripples and dunes), effectively reducing the total friction to consist of only grain friction (see Fig. 5: E. Plane bed) (Simons and Richardson, 1966). Thus, for low flows, the stage is higher than normal; conversely, for high flows, the stage is lower than normal. This phenomenon acts to reduce the variability between low and high flow stages in alluvial streams (Kennedy, 1983). The attendant effect on the actual rating may be readily envisaged.

[Click on top of figure to expand]

Simons and Richardson (1966).

Fig. 5   Forms of bed roughness in alluvial channels: (a) lower regime (left), and (b) upper regime (right).

A practical example of the short-term sedimentation effect is represented by the so-called autodredging phenomenon, which is well documented in the Upper Paraguay river, in Mato Grosso, Brazil (Ponce, 1995). This unusual phenomenon, to be interpreted loosely as the river's natural self-cleaning process, is a self-deepening of the mainstem Upper Paraguay to a minimum depth of 1.2 m (4 ft), except in the few instances where rock outcrops do not permit autodredging to take place. It should not escape our attention that the maintenance of an appreciable minimum flow depth/stage enhances both river fisheries, a desirable component of Nature, and inland navigation, an anthropogenic activity.

---

5.  LONG-TERM SEDIMENTATION EFFECTS

Rivers tend to subject their boundaries to recurrent cycles of erosion and deposition, at various spatial scales. Typical triggering mechanisms may be represented by landslides (Fig. 5) or nearby anthropogenic activities (Fig. 6). Normally, properly located gaging stations are not affected by long-term sedimentation effects; however, this cannot be guaranteed into the future. The possibility of shifts in rating due to long-term aggradation/degradation or, alternatively, shifts in river course (Fig. 7) must be a part of a sensible program of gaging site management.

Fig. 5   Landslide that has reached the Moyan river, near Tingo, Lambayeque, Peru (2008).

Fig. 6   Proposed damsite at La Calzada, La Leche river, Lambayeque, Peru (2008).

Fig. 7   Abandoned bridge due to change of stream course/alignment, Pirai river, Santa Cruz department, Bolivia (1989).

---

6.  ONLINE CALCULATION

Having explained in some detail the basic concepts of rating curve hydraulics, we now proceed to calculate the rating curve of a trapezoidal channel cross-section. To accomplish this objective, we use the online calculator ONLINECHANNEL15B with the following input data:

Input Data. Bottom width b = 10 m; flow depth y = 2 m; side slope z = 1; Manning's n = 0.015; and bottom slope S = 0.0003.

A summary of the results of the online calculator is shown in Fig. 8.

The rating equation is Q = α A ^β, in which α = 0.251, and β = 1.585.

---

7.  SUMMARY

A review of relevant concepts of rating curves in hydraulic and hydrologic engineering is accomplished. Four topics are discussed: (1) steady uniform flow rating; (2) unsteady flow rating; (3) short-term sedimentation effects; and (4) long-term sedimentation effects. The steady uniform flow rating is unique, i.e., it features a single-valued rating, i.e., a unique relation between discharge and stage. This is the most common situation in practice.

The unsteady flow rating features a histeresis, or loop, in the discharge-stage rating, which reflects directly the amount of wave diffusion of the unsteady flow feature (the diffusion wave). The size of the loop is directly related to the amount of wave diffusion of the passing flood.

The short-term sedimentation effect is predicated on the tendency of an alluvial river to minimize the changes in stage. This is accomplished by the flow itself modifying the roughness of the channel bed to increase/decrease form friction during low/high flows. This modification has the effect of reducing the stage variability as the flow varies from low to high.

The long-term sedimentation effect recognizes that rivers are the authors of their own geometry, and that they are recurrently subjected to incessant cycles of erosion and deposition, both of natural and human-induced causes. Therefore, the question of the permanence of a rating curve has to be taken against the reality of possible eventual geomorphic changes.

---

[Click on top of figure to expand]

Fig. 8   Tabular results of the online calculator ONLINECHANNEL15B.

---

REFERENCES

Kennedy, J. F. 1983. Reflections on rivers, research, and Rouse. Journal of Hydraulic Engineering ASCE, 109(10), 1257-1260.

Ponce, V. M. and D. B. Simons. 1977. Shallow wave propagation in open channel flow. Journal of Hydraulic Engineering ASCE, 103(12), 1461-1476.

Ponce, V. M. 1995. Hydrologic and environmental impact of the Parana-Paraguay Waterway on the Pantanal of Mato Grosso, Brazil: A reference study. San Diego State University, San Diego, California, August.

Simons, D. B., and E. V. Richardson. 1966. Resistance to flow in alluvial channels. Geological Survey Professional Paper 422-J, U.S. Government Printing Office, Washington, D.C.

---