ABSTRACT Rorabaugh's theoretical model of groundwater flow to a stream is used to estimate regional aquifer parameters in the Papaloapan River basin, in Southern Mexico (Rorabaugh, 1963). This is a large tropical basin, with 46,517 km2, a diversity of climatic conditions and a substantial interaction between surface and groundwater. Baseflow recession data is used to calculate time of storage, basin constant, and hydraulic diffusivity for ten locations throughout the basin. The results show reasonably good agreement with local geology, as assessed by geologic maps and pumping tests.

1.  INTRODUCTION

In groundwater hydrology, there is a need to estimate aquifer parameters such as time of storage (Hall, 1968; Ponce, 1989), basin constant (Rorabaugh and Simons, 1966) and hydraulic diffusivity (Freeze and Cherry, 1979). The estimation of these parameters based on stream flow recession data is possible using a theoretical model developed by Rorabaugh (1963) and extended by Rorabaugh and Simons (1966). Rorabaugh (1963) converted the heat-flow diffusion equation into groundwater units and, therefore, he was able to relate baseflow discharge to aquifer parameters.

We have applied Rorabaugh's model to base flow recession data from the Papaloapan River basin, in Southern Mexico. Our objective is to show that quality recession data can be used to estimate aquifer parameters with a high degree of confidence, thereby linking groundwater and surface water processes. These estimates complement those based on pumping tests, and could be used as reasonable estimates in the absence of field data (Moore, 1992).

2.  THE RORABAUGH MODEL

Rorabaugh (1963) developed a theoretical model for the groundwater discharge to a stream, assuming a basin having uniform, homogeneous, isotropic characteristics, i.e., of constant hydraulic conductivity, coefficient of storage, and aquifer thickness. The equation is:

q  =  2T (ho /a) e - (π 2 T t ) / (4 a 2 S )

(1)

in which q = groundwater discharge per unit of stream length, from one side; T = transmissivity, defined as the product of hydraulic conductivity and aquifer thickness (Freeze and Cherry, 1979); h_o = instantaneous head difference between water table and stream, measured from the groundwater divide; a = distance from stream to groundwater divide (aquifer half-width); S = coefficient of storage, and t = time. This equation is applicable after the stream flow recession is well established, i.e., after a critical time t_c such that (T t_c ) / (a ² S ) = 0.2 (Rorabaugh, 1963; Rutledge and Daniel, 1994; Mau and Winter, 1997).

Using Darcy's law, it can be shown that the quantity 2T(h_o /a ) is essentially a reference unit-width discharge q_o. Since Eq. 1 models the exponential decay of distributed groundwater discharge, Rorabaugh and Simons (1966) extended this equation to develop their at-a-station baseflow model:

Q  =  Qo e - (π 2 T t ) / (4 a 2 S )

(2)

in which Q = baseflow at time t; and Q_o = baseflow at time 0. Trainer and Watkins (1974) have used Rorabaugh's model to estimate areal transmissivities in the Upper Potomac river basin. More recent studies have applied Rorabaugh's model to estimate groundwater recharge in diverse hydrogeologic settings (Rutledge and Daniel, 1994; Mau and Winter, 1997; Sanz, 1997). Herein we extend it to estimate sub-basin aquifer parameters in a large tropical basin featuring a diversity of hydrogeologic and climatic settings.

3.  AQUIFER CHARACTERISTICS

Boussinesq (1877) linearized the equation governing groundwater flow and expressed it as a diffusion equation which can be solved more readily (Hall, 1968). With the diffusion analogy, a groundwater basin can be characterized in terms of the following parameters:

1. Time of storage t_s (Hall, 1968; Ponce, 1989; Tallaksen, 1995), a recession constant equal to:

4 a 2 S ts  =  ________             π 2 T

(3)

The time of storage is such that when t = t_s, the discharge has receded to 37 percent of its value at t = 0, i.e., it is a measure of the relative speed of the recession.

2. Basin constant K_b (Rorabaugh and Simons, 1966):

T Kb  =  _______             a 2 S

(4)

The basin constant (in T ^-1 units) combines the geometric and hydrogeologic properties of the aquifer into one convenient parameter.

3. Hydraulic diffusivity D (Freeze and Cherry, 1979):

T D  =   ____            S

(5)

The hydraulic diffusivity (in L² T ^-1 units) combines the hydrogeologic properties of the aquifer into one parameter characterizing a diffusion process.

4. APPLICATION TO PAPALOAPAN RIVER BASIN

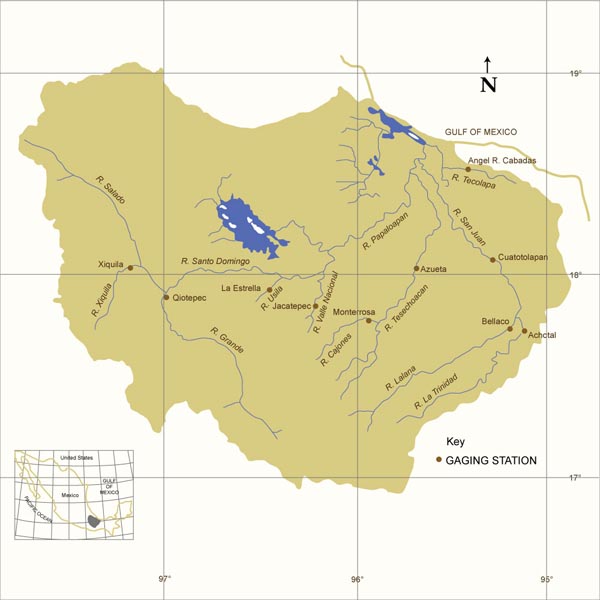
Rorabaugh's model was applied to streamflow recession data for the Papaloapan river basin, in the states of Veracruz and Oaxaca, Mexico (Fig. 1). This is a large tropical basin, of 46,517 km², which features a diversity of hydrogeologic and climatic settings.

Table 1 shows selected gaging stations, stream, location, mean annual precipitation and subbasin geometric characteristics. The hydraulic length, i.e., the length measured along the principal watercourse, was obtained from topographic maps. The aquifer width was estimated as the ratio of drainage area over hydraulic length. The climatic conditions range from very humid to arid, e.g., Rio Usila at La Estrella, with 4,805 mm of mean annual precipitation to Rio Xiquila at Xiquila, with 354 mm.

Table 1.  Gaging stations and basin geometric characteristics in Papaloapan river basin.
Gaging Station	Stream	Latitude	Longitude	Mean annual precipitation1 (mm)	Drainage area (km2)	Hydraulic length (km)	Aquifer width (km)
Achotal	La Trinidad	17° 46'	95° 09'	1620	2333	124.4	18.7
Angel R. Cabadas	Tecolapa	18° 35'	95° 26'	2255	125	24.4	5.1
Azueta	Tesechoacan	18° 05'	95° 43'	1533	1656	83.7	19.8
Bellaco	Lalana	17° 46'	95° 11'	1587	2917	115.5	25.3
Cuatotolapan	San Juan	18° 09'	95° 18'	1305	7090	167.4	42.3
Jacatepec	Valle Nacional	17° 52'	96° 12'	3906	1117	58.3	19.2
La Estrella	Usila	17° 55'	96° 26'	4805	774	34.1	22.7
Monterrosa	Cajones	17° 48'	95° 56'	2288	2870	111.6	25.7
Qiotepec	Grande	17° 54'	96° 59'	636	4832	76.3	63.3
Xiquila	Xiquila	18° 02'	97° 09'	354	1073	55.1	19.5
1 Annual isohyets of Mexico, 1931-90, Regions 28 (Papaloapan) and 29 (Coatzacoalcos).

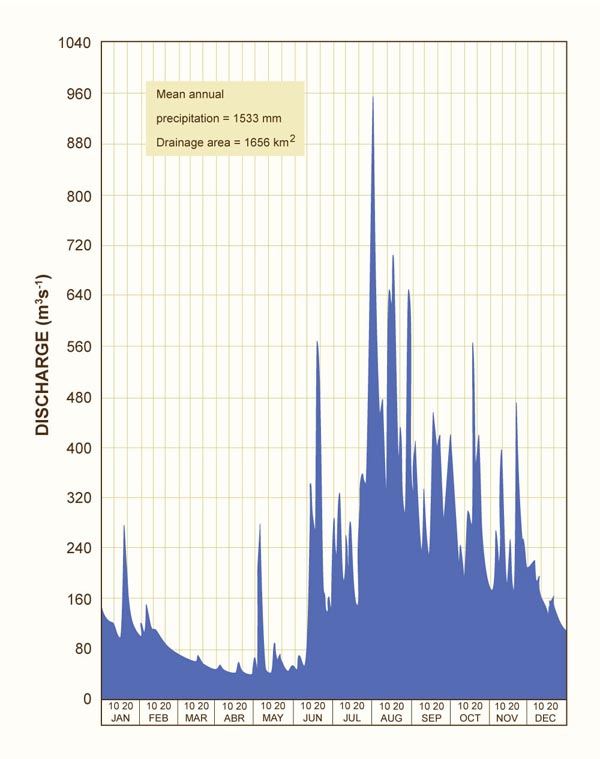
Figure 2 shows the 1972 hydrograph for Rio Tesechoacan at Azueta (Comision del Papaloapan, 1972), typical of the streamflow data for the Papaloapan river basin. Baseflow recession data for the two-year period 1971-72 were assembled for the selected gaging stations. For each station, several baseflow recession periods at the end of the dry season, lasting from 5 to 18 d, were selected for analysis. For each period, daily values of time of storage, basin constant, and hydraulic diffusivity were calculated, and averaged to obtain period values. For each station, the average period values were again averaged to obtain mean station values.

Table 2 shows calculated aquifer parameters for the ten selected subbasins, which comprise a diversity of hydrogeologic and climatic settings. The time of storage varies between 23.49 and 116.64 d; the basin constant varies between 0.00586 and 0.01725 d ^-1; the hydraulic diffusivity varies between 0.058 and 15.619 km² d ^-1.

Table 2.  Aquifer characteristics in the Papaloapan river basin.
Gaging Station	Stream	Time of storage1			Basin constant	Hydraulic diffusivity
		__ x (d)	s (d)	Cv	d-1	km2d-1	m2s-1
Achotal	La Trinidad	51.28	8.51	0.166	0.00790	0.694	8.037
Angel R. Cabadas	Tecolapa	46.03	9.30	0.202	0.00880	0.058	0.666
Azueta	Tesechoacan	57.42	8.35	0.145	0.00706	0.690	7.983
Bellaco	Lalana	53.97	14.93	0.277	0.00751	1.196	13.845
Cuatotolapan	San Juan	69.12	16.20	0.234	0.00586	2.627	30.403
Jacatepec	Valle Nacional	35.20	9.54	0.271	0.01151	1.056	12.228
La Estrella	Usila	25.05	5.21	0.208	0.01618	2.079	24.061
Monterrosa	Cajones	23.49	6.04	0.257	0.01725	2.850	32.988
Qiotepec	Grande	26.00	6.94	0.267	0.01559	15.619	180.778
Xiquila	Xiquila	116.64	18.28	0.157	0.00347	0.329	3.811
1 __     x = mean; s = standard deviation; Cv = coefficient of variation.

Table 3 shows predominant rock types, varying from igneous (basalt) to sedimentary (sandstone, limestone) to metamorphic (schist) (Geologic maps of Mexico, 1:250,000 scale, published by INEGI).

Table 3.  Predominant rock types of subbasins in Papaloapan river basin. 1
Gaging Station	Stream	Predominant rock types
Achotal	La Trinidad	Sandstone, schist, calcareous sandstone and limestone
Angel R. Cabadas	Tecolapa	Basalt, basaltic tuff
Azueta	Tesechoacan	Sandstone, calcareous sandstone, limestone and conglomerate
Bellaco	Lalana	Sandstone, schist, calcareous sandstone and conglomerate
Cuatotolapan	San Juan	Sandstone, limestone, schist, calcareous sandstone and conglomerate
Jacatepec	Valle Nacional	Schist, calcareous sandstone and limestone
La Estrella	Usila	Schist, calcareous sandstone and limestone
Monterrosa	Cajones	Schist, andesite, calcareous sandstone, limestone and monzonite
Qiotepec	Grande	Metamorphosed granite, schist, limestone, shale, calcareous sandstone, sandstone and conglomerate
Xiquila	Xiquila	Limestone, sandstone, conglomerate and andesite
1 Orizaba (E14-6), Oaxaca (E14-9), Coatzacoalcos (E15-4), and Minatitlan (E15-7) maps.

Table 4 shows predominant rock types grouped in terms of time of storage.

Table 4.  Predominant rock types grouped in terms of time of storage.
Group	Gaging station	Time of storage (d)	Predominant rock types
I	Jacatepec, La Estrella, Monterrosa and Quiotepec	23.5 - 35.2	Schist, metamorphosed granite, calcareous sandstone, limestone, sandstone and shale
II	Angel R. Cabadas	46.0	Basalt, basaltic tuff
III	Achotal, Azueta, Bellaco and Cuatotolapan	51.3 - 69.1	Sandstone, calcareous sandstone, limestone, conglomerate and schist
IV	Xiquila	116.6	Limestone, sandstone, conglomerate and andesite

Group I (Jacatepec, La Estrella, Monterrosa, and Quiotepec) has short time of storage (23 to 35 d). These subbasins are located inland south to southwest (Fig. 1), across the mountain ranges, with climate varying from very humid to arid, and featuring primarily metamorphic and some sedimentary rocks. These aquifers drain relatively fast.

Group II (Angel R. Cabadas) has intermediate time of storage (46 d). This subbasin is located in the coastal northeast, with a humid climate and basaltic rocks.

Group III (Achotal, Azueta, Bellaco, and Cuatotolapan) has long time of storage (51 to 69 d). These subbasins are located in the eastern plains, with humid climate and primarily sedimentary and some metamorphic rocks.

Group IV (Xiquila) has very long time of storage (116 d). This subbasin is located inland to the southwest, draining the Sierra Madre, with an arid climate and primarily sedimentary and some volcanic rocks.

The group I aquifers, where schist predominates, are unable to sustain baseflow for long periods. Conversely, the group IV aquifer, where limestone predominates, is able to sustain baseflow for very long periods.

5. FIELD VERIFICATION

Table 5 shows geographic and hydrogeologic data for seven wells located within the Papaloapan river basin. The values of hydraulic diffusivity, although restricted to the north-central portion of the basin, are seen to compare favorably with those of Table 2. Lack of additional data in other parts of the basin precluded a more thorough comparison.

Table 5.  Pumping stations, location and hydrogeologic characteristics in Papaloapan river basin.1
Pumping station	Well No.	Latitude	Longitude	Transmissivity (m2/s)	Coefficient of storage	Hydraulic diffusivity (m2/s)
San Jose Independencia	03	18° 23'	96° 03'	0.0550	0.00250	22.000
Cosamaloapan	05	18° 22'	95° 48'	0.0021	0.01000	0.210
Paso Carretas	09	18° 41'	96° 08'	0.0470	0.06800	0.690
Rio Moreno	11	18° 38'	96° 14'	0.0260	0.00790	3.290
Cuyucuenda	13	18° 47'	96° 16'	0.0082	0.00043	19.070
Piedras Negras	14	18° 46'	96° 10'	0.0460	0.09400	0.489
Ignacio de la Llave	15	18° 43'	96° 59'	0.0043	0.09400	0.046
1 Data obtained from the National Water Commission, Jalapa, Mexico.

6. SUMMARY

Rorabaugh's model has been used to estimate regional aquifer parameters in the Papaloapan river basin, in southern Mexico. Time of storage, basin constant, and hydraulic diffusivity are calculated. The results show reasonably good agreement with local geology, as assessed with geologic maps and pumping tests. This underscores the promise of this approach to estimate regional aquifer parameters using baseflow recession data.

ACKNOWLEDGEMENTS

The present study was performed while S. Kumar was at San Diego State University, on leave from the National Institute of Hydrology, Roorkee, India. His leave was funded by the United Nations Development Programme. The pumping data was obtained from the National Water Commission, Jalapa, Mexico, through the auspices of Horacio Rubio, regional manager.

REFERENCES

Boussinesq, J. 1877. Essai sur la theories des eaux courantes. Memoires presentes par divers savants a l'Academic des Sciences de l'Institut National de France, Tome XXIII,No. 1.

Comisión del Papaloapan. 1972. Boletín Hidrométrico No. 19: 1971-1972. Secretaría de Recursos Hidráulicos, Mexico City, Mexico.

Freeze, R. A., and Cherry. J. A. 1979. Groundwater. Prentice Hall, Englewood Clis, New Jersey.

Hall, F. R. 1968. Base-flow recessions - A review. Water Resources Research, 4(5), 973-983.

Mau, D. P., and Winter, T. C. 1997. Estimating groundwater recharge from streamflow hydrographs for a small mountain watershed in a temperate humid climate, New Hampshire, USA. Ground Water, 35(2), March-April, 291-304.

Moore, G. K. 1992. Hydrograph analysis in a fractured rock terrain. Ground Water, 30(3), May-June, 390-395.

Ponce, V. M. 1989. Engineering Hydrology: Principles and Practices. Prentice Hall, Englewood Cliffs, New Jersey.

Rorabaugh, M. I. 1963. Estimating changes in bank storage in groundwater contributions to streamflow. International Association of Scientic Hydrology, Publication No. 63, 432-441.

Rorabaugh, M. I., and Simons, W. D. 1966. Exploration of methods of relating groundwater to surface water, Columbia river basin - second phase. U.S. Geological Survey Open-file Report, March.

Rutledge, A. T., and Daniel, III, C. C. 1994 Testing an automated method to estimate groundwater recharge from streamflow records. Ground Water, 32(2), March-April, 180-189.

Sanz Pérez, E. 1997. Estimation of basinwide recharge rates using springflow, precipitation,and temperature data. Ground Water, 35(6), November-December, 1958-1965.

Tallaksen, L. M. 1995. A review of baseflow recession analysis. Journal of Hydrology, 165,349-370.

Trainer, F. W., and Watkins Jr., F. A. 1974. Use of base-runoff recession curves to determine real transmissivities in the Upper Potomac River Basin. U.S. Geological Survey Journal of Research, 2(1), 125-131.