|
¿CUÁL ES LA RELACIÓN DE ASPECTO DE UNA CORRIENTE ALUVIAL?
Universidad Estatal de San Diego,
California, EE.UU.
1. INTRODUCCIÓN
Las corrientes aluviales son autoformadas, es decir, su forma, caracterizada por
su profundidad y su ancho, obedece a las leyes de la mecánica, propiamente
dentro del campo de la hidráulica fluvial.
El momento integra la fuerza actuante en el tiempo, mientras que la energía
integra la misma fuerza en el espacio; por lo tanto, no son independientes.
En flujo permanente en canales abiertos, las ecuaciones de masa y
energía se utilizan para resolver las variables de flujo
(profundidad y pendiente). En flujo no permanente, las ecuaciones
de masa y momento se utilizan para el mismo propósito. Esta realidad
deja el cálculo del ancho de la corriente sin determinar.
El ancho tendrá que ser calculado utilizando principios de hidráulica fluvial.
Lane y sus colaboradores (1959) han desarrollado un enfoque mecanístico para
calcular el ancho en una corriente autoformada. La teoría ha sido revisada
recientemente por Ponce y Jiang (2020).
La aplicación de la metodología de Lane puede servir para arrojar
luz adicional sobre importantes problemas de inundaciones y otros problemas relacionadas con la sedimentación fluvial
2. LA TEORÍA DE LANE
El tamaño de la sección transversal de una corriente fluvial
en equilibrio, formado con materiales no cohesivos, depende
del nivel máximo de caudal. Lane y sus colaboradores (1959), utilizando principios de
hidráulica fluvial, demostraron que la
forma de la sección transversal de equilibrio es función
de:
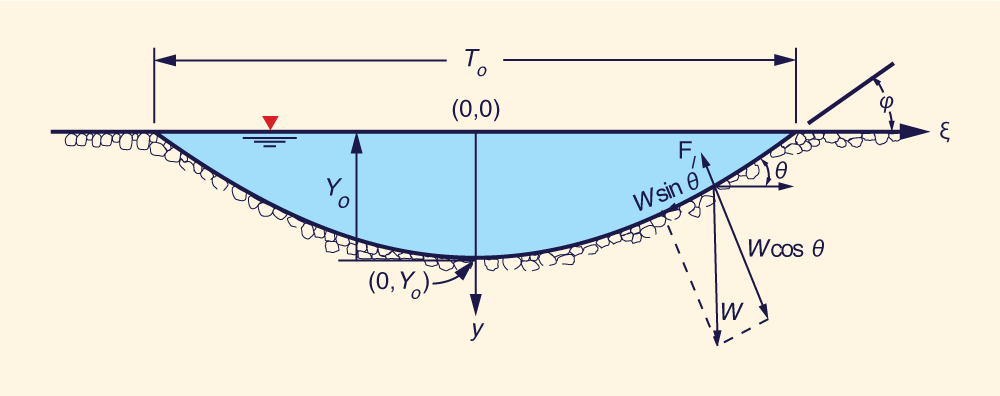
Las principales consideraciones de Lane y sus colaboradores son las siguientes:
La pendiente lateral de la sección transversal de la corriente, inmediatamente
encima de la superficie del agua, es igual al ángulo de fricción interna φ
del material aluvial no cohesivo
Las partículas en la frontera de la corriente
están en condición de movimiento incipiente.
Las partículas se mantienen en su lugar en virtud de su peso sumergido
resuelto en una dirección normal al lecho de la corriente.
La fuerza de tracción actúa en la dirección del flujo y es igual
al peso de la columna de agua ubicada encima del área sobre la que actúa la fuerza.
Se asume que el canal es prismático,
con corrientes secundarias insignificantes y ausencia de remanso.
3. RESULTADOS
La derivación de la teoría de Lane y sus colaboradores (1959) ha sido ampliamente documentada
por Ponce y Jiang (2020): Sección 3.
En ese informe, la Ec. 57,
reproducida aquí como Ec. 1, es la ecuación derivada por Lane
para la relación ancho-profundidad, o relación de aspecto de un canal
autoformado tallado en material no cohesivo en condiciones de equilibrio:
en la cual To = ancho de superficie de la corriente,
Yo = profundidad máxima (en el centro),
φ = ángulo de fricción interna
del material no cohesivo, β = relación fuerza de elevación / fuerza de arrastre (fricción),
y
La Tabla 1 muestra la relación de aspecto calculada usando la Ec. 1,
para ángulos de fricción interna en
el rango 5 ≤ φ ≤ 45°, a intervalos de 5°,
y la relación fuerza de elevación a arrastre en el rango
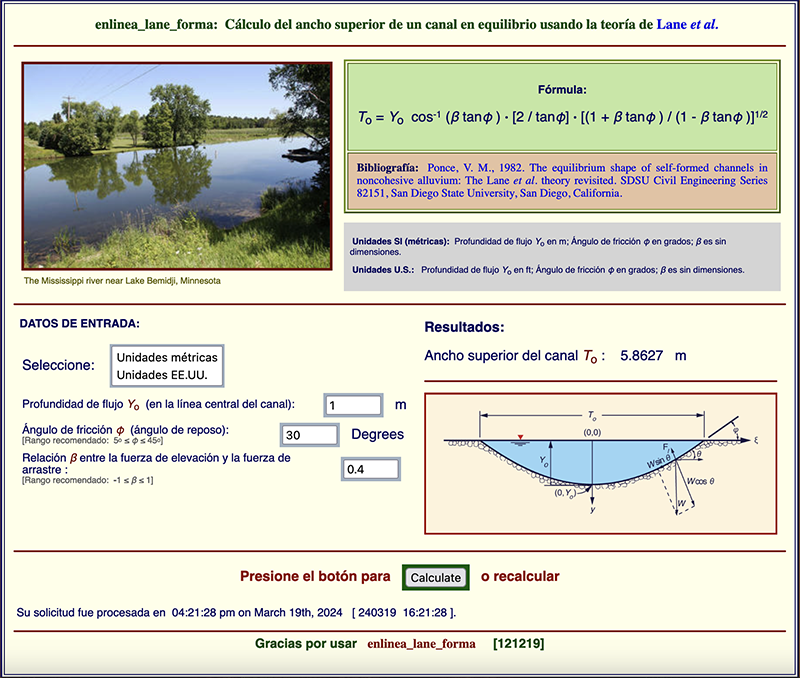
4. CÁLCULO EN LÍNEA
La Ecuación 1 puede resolverse con la ayuda del calculador
ENLINEA_LANE_FORMA.
5. EPÍLOGO
La relación de aspecto de una corriente autoformada en material aluvial
no cohesivo
se ha calculado utilizando la teoría de Lane y sus colaboradores (1959).
La relación de aspecto To /Yo
se expresa en términos del ángulo de fricción interna φ del material
que forma el lecho de la corriente y la relación
BIBLIOGRAFÍA
Apperley, L. W. 1968. The effect of turbulence
on sediment entrainment. Thesis submitted
to the School of Engineering, University of
Auckland, Auckland, New Zealand, in partial fulfillment for the
requirements for the degree
of Doctor of Philosophy, January.
ASCE, 1975. Sedimentation Engineering. Manuals and Reports on Engineering Practice, Manual 54,
Vito A. Vanoni, editor, New York.
ASCE, 2007. Sedimentation Engineering: Processes, Measurements, Modeling, and Practice.
Manuals and Reports on Engineering Practice, Manual 110,
Marcelo H. Garcia, editor, New York.
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, Inc, New York.
Lane, E. W., P. N. Lin, y H. K. Liu. 1959.
The most efficient stable channel for comparatively clean water in noncohesive material.
Report CER-59HKL, Colorado State University, Fort Collins, Colorado, April.
Ponce, V. M., y S. Jiang. 2020.
The equilibrium shape of self-formed channels in noncohesive alluvium.
Online report.
Ponce, V. M. 2014.
Fundamentals of Open-channel Hydraulics.
Texto en línea. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 240319 |