El número de la curva SCS

Víctor M. Ponce

Universidad Estatal de San Diego,
California, EE.UU.

[Versión original 1996, en Inglés]


RESUMEN

Se revisan los fundamentos conceptuales y empíricos del método del número de la curva. El método es un modelo conceptual de abstracción hidrológica de tormentas. Su objetivo es estimar la profundidad de escorrentía directa a partir de la profundidad de la lluvia de tormenta, con base en un parámetro denominado número de la curva. El método no tiene en cuenta la variabilidad espacial y temporal de la infiltración y otras pérdidas; más bien, los agrega en un cálculo de la pérdida total de profundidad para un evento y un área de drenaje dados. El método describe tendencias medias, lo que le impide ser perfectamente predictivo. La variabilidad observada en los números de la curva, más allá de la que pueda atribuirse al tipo de suelo, uso/tratamiento del terreno, y condición de la superficie, está incorporada en el concepto de condición de humedad antecedente. El método se usa ampliamente en los Estados Unidos y otros países a nivel global. Las ventajas percibidas del método son: (1) simplicidad; (2) predictabilidad; (3) estabilidad; (4) dependencia de un solo parámetro; y (5) capacidad de respuesta a las principales propiedades de las cuencas hidrográficas (tipo de suelo, uso/tratamiento del terreno, condición hidrológica de la superficie, y condición de humedad antecedente). Las desventajas son: (1) su marcada sensibilidad al número de la curva; (2) la ausencia de una guía clara sobre cómo variar la condición de humedad antecedente; (3) la precisión variable del método para diferentes biomas; (4) la ausencia de una recomendación explícita para tener en cuenta los efectos de escala espacial; y (5) la fijación de la tasa de extracción inicial en λ = 0.2, desalentando una posible regionalización basada en el entorno geológico y climático.

1.  INTRODUCCIÓN

Definición, base

El método del número de la curva para la estimación de la escorrentía directa de las tormentas está bien establecido en la ingeniería hidrológica y los análisis de impacto ambiental. Su popularidad se basa en su conveniencia, su simplicidad, sus orígenes gubernamentales y su capacidad de respuesta a cuatro propiedades de cuencas fácilmente discernibles: Tipo de suelo, uso/tratamiento del terreno, condición de la superficie y condición antecedente de humedad.

Historia

El método fue desarrollado en 1954 por el Servicio de Conservación de Suelos del USDA (Rallison 1980), y se describe en la Sección 4 del Manual de Ingeniería Nacional del Servicio de Conservación de Suelos (SCS): Hidrología (NEH-4) (SCS 1985). La primera versión del manual que contiene el método se publicó en 1954. Las revisiones posteriores siguieron en 1956, 1964, 1965, 1971, 1972, 1985 y 1993. Desde su inicio, el método contó con el apoyo total de una agencia federal y, además, llenó un nicho tecnológico estratégico. Por lo tanto, se estableció rápidamente en la práctica hidrológica, con numerosas aplicaciones en los Estados Unidos y otros países. La experiencia con el número de la curva sigue aumentando hasta la fecha (Bosznay 1989; Hjelmfelt 1991; Hawkins 1993; Steenhuis et al. 1995).

Credibilidad

Sin embargo, la credibilidad y aceptación del método ha sufrido debido a su origen como metodología del gobierno, lo cual lo aisló efectivamente de los rigores de la revisión por pares. Aparte de la información contenida en NEH-4, que no pretendía ser exhaustiva (Rallison y Cronshey 1979), hasta la fecha no se dispone de una descripción completa de los fundamentos del método, a pesar de algunos intentos recientes dignos de mención (Rallison 1980; Chen 1982; Miller y Cronshey 1989).

Estado actual

En las siete décadas que han transcurrido desde el inicio del método, la mayor disponibilidad de computadoras ha llevado al uso de modelos hidrológicos complejos, muchos de los cuales incorporan el método del número de la curva. Por lo tanto, surge naturalmente la pregunta: ¿Cuál es el estado del método del número de la curva en una jerarquía postulada de modelos de abstracción hidrológica? (Miller y Cronshey 1989; Rallison y Miller 1982). ¿Ha madurado hasta gozar de una aceptación y un uso generalizados? O, como sugieren algunos de sus detractores, está ya obsoleto, es un remanente de tecnología antigua, y necesita una revisión o un reemplazo total (Smith y Eggert 1978; Van Mullem 1989).

Una revisión eficaz del método requeriría una comprensión más clara de sus propiedades que la que está actualmente disponible (Woodward 1991; Woodward y Gburek 1992). Un reemplazo absoluto, si se desarrollara uno, probablemente prescindiría de parte o de todos los extensos datos sobre grupos hidrológicos de suelos y clases de uso/tratamiento terreno que se han desarrollado para la mayor parte de los Estados Unidos (Miller y Cronshey 1989). A más de 4.000 suelos de los Estados Unidos se les ha asignado un grupo hidrológico de suelos (Rallison 1980). Además, un reemplazo o revisión no puede evitar depender de varias de esas mismas características que ahora forman parte del método. Por lo tanto, se ha hecho necesario examinar el método para arrojar luz adicional sobre sus fundamentos y delinear sus capacidades y limitaciones, para que los usuarios puedan seguir utilizando el método sin temor a una desaparición inminente.

Objetivos presentes

Por lo tanto, los objetivos de este trabajo son los siguientes:

   1. Examinar críticamente el método del número de la curva,

   2. Clarificar sus bases conceptual y empírica,

   3. Delinear sus capacidades, limitaciones y usos, y

   4. Identificar áreas de investigación en el método del número de la curva.

Característica conceptual: Simpleza

A lo largo de los años, la base conceptual del método del número de la curva ha sido objeto de apoyo y críticas. Un modelo conceptual comparte la simplicidad de los modelos empíricos y la aplicabilidad más amplia de los modelos físicos más rigurosos (Dooge 1977). Siendo conceptual, el método del número de la curva es simple, y en esto reside la raíz de su popularidad. Por otro lado, es precisamente por esta razón que el método no ha sido aceptado entre los partidarios de modelos alternativos, que incluyen los modelos con base física (Smith 1976). A juzgar por la experiencia, la elección entre modelos conceptuales y físicos de abstracción hidrológica es difícil, particularmente con respecto a la infiltración (Branson et. al. 1981; Savabi et. al. 1990; Hjelmfelt 1991).

Branson et. al. (1962, 1981), entre otros, ha argumentado que los modelos conceptuales más simples no son necesariamente inferiores a los modelos de base física más complejos. Estos últimos pueden hacer un buen trabajo al describir los procesos físicos, pero esto suele ser en desmedro de los aspectos químicos y biológicos. En muchos casos, los procesos como la formación de costras en la superficie, la contracción y el hinchamiento de suelos arcillosos, gases atrapados, la estructura y descomposición de las raíces y la macro y microfauna del suelo pueden ser de tal importancia que invaliden en gran medida un enfoque estrictamente físico de la modelación de infiltración (Le Bissonnais y Singer 1993).

2.   MODELOS AGREGADOS VERSUS DISTRIBUIDOS

El método del número de la curva es un modelo de pérdida (abstracción) por infiltración, aunque también puede tener en cuenta las pérdidas por intercepción y almacenamiento en superficie a través de su componente de abstracción inicial. Tal como se desarrolló originalmente, el método no está diseñado para tener en cuenta la evaporación y la evapotranspiración (pérdidas a largo plazo).

Tipo de modelo: Agregado o distribuido

Un modelo de pérdida por infiltración puede ser agregado o distribuido. El modelo agregado agrupa las variaciones espaciales y temporales en un valor de la profundidad de infiltración total para una profundidad de tormenta y una cuenca dadas. El modelo distribuido describe tasas de infiltración instantánea y/o local, a partir de las cuales se obtiene finalmente una profundidad de infiltración total mediante una adecuada integración en el tiempo y el espacio. El método del número de la curva se desarrolló originalmente como un modelo agregado (espacial y temporal), utilizado para convertir la profundidad de la tormenta en volumen de escorrentía directa. Hasta la fecha, se utiliza principalmente como un modelo agregado de la manera especificada por el Manual NEH-4 (SCS 1985). Sin embargo, algunos investigadores, en particular Smith (1976), Aron et. al. (1977), Chen (1975, 1976, 1982) y Hawkins (1978a, 1980) han desarrollado fórmulas equivalentes de capacidad de infiltración basadas directa o indirectamente en el método del número de la curva. Esto extiende efectivamente el método al dominio de la modelación distribuida, aunque las instancias de este tipo de uso parecen ser relativamente infrecuentes. Las fórmulas de infiltración existentes como Green y Ampt (1911), Horton (1933) y Philip (1957) describen tasas de infiltración instantánea y/o local y, por lo tanto, son adecuadas para la modelación distribuida.

Las ventajas relativas de la modelación distribuida frente a la modelación agregada no son fáciles de discernir. Con respecto a las capacidades de infiltración, la variabilidad espacial y temporal que prevalece en casi todos los escenarios prácticos no suele favorecer el enfoque distribuido, a menos que la naturaleza de esta variabilidad pueda incorporarse específicamente al modelo, lo cual no es una tarea fácil (Miller y Cronshey 1989). El hacer caso omiso de esta variabilidad, o no contabilizarla de una manera realísta, equivale en un sentido real a agrupar. Por lo tanto, los modelos agregados deben su existencia a nuestra incapacidad para explicar adecuadamente la variabilidad intrínseca de los fenómenos naturales. Lo que esto significa en la práctica es que un modelo agregado no es necesariamente malo. Más bien, es una forma práctica de sustituir el proceso distribuido más complejo mientras se intenta preservar las características principales del prototipo.

Descripción puntual o espacial

Una medición de la tasa de infiltración, o capacidad de infiltración, por más precisa que sea, solo puede describir la tasa en el punto de medición (Miller y Cronshey 1989). La extrapolación a un área más grande equivale a agrupar. De hecho, una profundidad de infiltración concentrada es una declaración de una tasa de infiltración promediada espacial y temporalmente (por pequeña que sea la parcela de muestreo), con todas las ventajas y desventajas que esto implica. La ventaja es que el método conserva las características medias de los fenómenos; la desventaja es que el método no describe específicamente la variabilidad espacial y/o temporal. Sin embargo, se han desarrollado algunas interpretaciones del método del número de la curva en términos de la distribución espacial de las profundidades de pérdida (Hawkins 1982; Hawkins y Cundy 1982).

En la práctica, una cantidad aceptable de agrupamiento es función de la escala del problema. Para problemas de pequeña escala, por ejemplo, parcelas medidas en metros cuadrados o hectáreas, un intento de determinar la variabilidad espacial y temporal de la capacidad de infiltración puede justificarse mediante mediciones de campo detalladas. Sin embargo, a medida que la escala aumenta a cientos de hectáreas y decenas de kilómetros cuadrados, la imposibilidad práctica de recopilar cantidades cada vez mayores de datos de infiltración hace que agruparlos sea una necesidad absoluta en la modelación de infiltración. Tarde o temprano, se tendrá que introducir una cierta cantidad de promedios espaciales. Además, considerando que el promedio espacial está implícito en la naturaleza de los datos de lluvia a cualquier escala, se presenta un caso fuerte a favor del agrupamiento como una táctica de facto de la modelación.

3.   CONVERSIÓN DE LLUVIA A ESCORRENTÍA

La conversión de la lluvia en escorrentía es la pieza central de la modelación de aguas superficiales. Una expresión elemental de conservación de la masa es:

Modelo de escorrentía

Q  = P - L
(1)

en la cual Q = escorrentía; P = precipitación; y L = pérdidas, ó abstracciones hidrológicas.

La cuantificación de las abstracciones hidrológicas puede ser una tarea compleja. Éstas se dividen en cinco categorías:

Abstracciones

  1. Almacenamiento de intercepción en un entorno rural, por la vegetación, follaje, tallos y basura y en un entorno urbano, por las características culturales del paisaje;

  2. Almacenamiento de superficie en estanques, charcos y otros lugares de almacenamiento temporal generalmente pequeños;

  3. Infiltración al subsuelo para alimentar y reponer la humedad del suelo, el interflujo y el flujo de agua subterránea;

  4. Evaporación de cuerpos de agua como lagos, embalses, arroyos y ríos, así como de la humedad en el suelo sin vegetación; y

  5. Evapotranspiración de todo tipo de vegetación.

De estos cinco tipos de abstracciones hidrológicas, la infiltración es la más importante para el análisis de tormentas (a corto plazo). La evaporación y la evapotranspiración son las más importantes para las evaluaciones de rendimiento estacionales o anuales (a largo plazo). Las dos pérdidas restantes (intercepción y almacenamiento de superficie) suelen tener una importancia secundaria.

Aplicabilidad

El método del número de la curva es un modelo de pérdida por infiltración; por lo tanto, su aplicabilidad se limita a modelar pérdidas de tormentas. Salvo modificaciones apropiadas, el método no debe usarse para modelar la respuesta hidrológica a largo plazo de una cuenca. No obstante, se reconoce que el método se ha utilizado en varios modelos de simulación hidrológica a largo plazo desarrollados en las últimas dos décadas (Williams y LaSeur 1976; Huber et. al. 1976; Knisel 1980; Soni y Mishra 1985), con diversos grados de éxito (Woodward y Gburek 1992). Dado que el método del número de la curva (desarrollado por SCS) no modela la evaporación y la evapotranspiración, su uso en la simulación hidrológica a largo plazo debe limitarse a modelar las pérdidas de tormentas y la escorrentía superficial asociada (Boughton 1989).

Ponce y Shetty (1995) han desarrollado recientemente un modelo conceptual del balance hídrico anual de una cuenca. El modelo consiste en la separación secuencial de: (1) la precipitación anual en escorrentía superficial y humectación; y (2) la humectación en flujo base y vaporización. El modelo de Ponce y Shetty se basa en un concepto similar al del número de la curva. Sin embargo, para una aplicación dada, el valor del parámetro de retención anual no tiene ninguna relación con el número de curva convencional.

4.  MODOS DE GENERACIÓN DE ESCORRENTÍA SUPERFICIAL

Para aclarar la base del método del número de la curva, se revisan aquí los procesos de generación de escorrentía superficial. La escorrentía superficial es generada por una variedad de flujos superficiales y cercanos a la superficie, de los cuales algunos de los más importantes son:

Modelos de escorrentía superficial

  1. Flujo Hortoniano de superficie,

  2. Flujo de saturación de superficie,

  3. Flujo a través del terreno,

  4. Flujo de área parcial,

  5. Intercepción directa en los canales, y

  6. Fenómenos superficiales, como el desarrollo de costras, capas hidrofóbicas de suelo, y suelo congelado.

El flujo hortoniano describe el proceso que tiene lugar cuando la intensidad de precipitación excede la capacidad de infiltración, generalmente al comienzo de una tormenta (o temporada), cuando es más probable que el perfil del suelo esté seco. La diferencia de intensidad de precipitación menos capacidad de infiltración es la intensidad de precipitación efectiva, la cual se convierte en escorrentía superficial.

El flujo de saturación describe el proceso que tiene lugar después de que el perfil del suelo se ha saturado, ya sea por eventos de precipitación anteriores o por un volumen suficiente de lluvia dentro del mismo evento. En este punto, cualquier lluvia adicional, independientemente de su intensidad, se convertirá en escorrentía superficial. El flujo de saturación generalmente ocurre durante una tormenta poco frecuente, o hacia el final de una temporada particularmente húmeda, cuando es probable que el suelo ya esté húmedo debido a tormentas anteriores.

El flujo a través del terreno prevalece en áreas densamente vegetadas con coberturas de suelo que contienen capas menos permeables, superpuestas a un lecho rocoso relativamente impermeable no meteorizado (Kirkby y Chorley 1967). Estrictamente hablando, el flujo a través de terreno no es una escorrentía directa (superficial), ya que el flujo tiene lugar principalmente como flujo intermedio o flujo lateral inmediatamente debajo de la superficie del terreno. Sin embargo, la respuesta relativamente rápida del flujo a través del terreno ocurre en el mismo período que la escorrentía superficial y, por lo tanto, generalmente se considera como un modo de generación de escorrentía superficial.

El flujo de área parcial se desarrolló a partir del reconocimiento de que las estimaciones de escorrentía mejoraron asumiendo que sólo la lluvia en una parte pequeña y bastante constante de cada cuenca de drenaje puede contribuir al escorrentía directa (Kirkby y Chorley 1967). Por lo tanto, el escorrentía de área parcial se puede interpretar como una combinación de flujo en las laderas superiores y flujo superficial de saturación en las laderas inferiores (Chorley 1978; Branson et. al. 1981; Hawkins 1981).

La intercepción directa en los canales se refiere a la escorrentía que se origina por la lluvia que cae directamente en los canales. Este modo de generación de escorrentía superficial puede ser importante en redes de canales densos, donde la intercepción directa de canales puede ser la fuente principal del flujo de los arroyos (Hawkins 1973).

Los fenómenos superficiales incluyen procesos como el desarrollo de una corteza impermeable, capas hidrófobicas de suelo, y suelo congelado, que hacen que la superficie del terreno sea impermeable, lo cual promueve la escorrentía superficial. Por ejemplo, una costra superficial puede desarrollarse después de la erosión por salpicadura en una cuenca hidrográfica erosionada, afectada adversamente por actividades humanas o un peligro natural como un incendio. Bajo un conjunto específico de circunstancias, incluido el tipo y la textura del suelo, el limo arrastrado por la erosión por salpicadura puede depositarse en la superficie y crear una costra delgada que eventualmente reduce la velocidad de infiltración a un nivel insignificante. Por lo tanto, cualquier lluvia adicional será convertida en escorrentía superficial. Este modo de generación de escorrentía superficial es típico de ambientes semiáridos, donde pueden ocurrir grandes cantidades de escorrentía superficial aunque el perfil del suelo subyacente, debajo de una capa relativamente delgada, permanezca sustancialmente seco ("Influences" 1940; Le Bissonnais y Singer 1993).

5.  ANTECEDENTES HISTÓRICOS

Antecedentes

Los orígenes de la metodología del número de la curva se remontan a las miles de pruebas de infiltrómetro realizadas por SCS a fines de la década de 1930 y principios de la de 1940. La intención era desarrollar datos básicos para evaluar los efectos del tratamiento de cuencas hidrográficas y las medidas de conservación del suelo en el proceso de lluvia-escorrentía. Un catalizador importante para el desarrollo e implementación de la metodología del número de la curva fue la aprobación de la Ley de Protección de Cuencas Hidrográficas y Prevención de Inundaciones en agosto de 1954. Se esperaba que los estudios asociados con la planificación de proyectos de pequeñas cuencas hidrográficas requirieran una mejora sustancial en el cálculo hidrológico dentro de SCS (Rallison 1980).

Sherman (1942, 1949) había propuesto graficar la escorrentía directa versus la profundidad de precipitación. Sobre la base de esta idea, Mockus (1949) propuso que las estimaciones de la escorrentía superficial para las cuencas hidrográficas no calibradas podrían basarse en información sobre suelos, uso de la tierra, antecedentes de precipitación, duración de la tormenta y temperatura promedio anual. Además, combinó estos factores en un parámetro empírico b que caracteriza la relación entre la profundidad de precipitación P y la profundidad de escorrentía Q (Rallison 1980):

Q  = P (1 - 10 -bP ) (2)

Andrews (informe no publicado, 1954), utilizando datos de infiltrómetros de Texas, Oklahoma, Arkansas y Luisiana, desarrolló un procedimiento gráfico para estimar la escorrentía de lluvia para varias combinaciones de textura del suelo, tipo y cantidad de cobertura, y prácticas de conservación. La asociación se denominó complejo cobertura-suelo (Miller y Cronshey 1989).

La relación empírica lluvia-escorrentía P - Q (Ec. 2) de Mockus y el complejo cobertura-suelo de Andrews fueron los fundamentos de la relación conceptual lluvia-escurrimiento incorporado en la primera versión de NEH-4 (Hidrología 1954). El método, referido como el número de la curva de escorrentía, tiene las siguientes características:

Características

  1. La profundidad de escorrentía Q está limitada al rango 0 ≤ Q ≤ P, asegurando su estabilidad.

  2. Conforme la profundidad de precipitación P crece sin límites (P → ∞), la retención real (P - Q) se aproxima asintóticamente a un valor constante S. Este valor constante, denominado en NEH-4 como "retención potencial máxima", y aquí simplemente como "retención potencial", caracteriza el potencial de la cuenca para retener la humedad de la tormenta y, por lo tanto, su potencial de escorrentía directa.

  3. Una ecuación de escorrentía relaciona Q con P, y un parámetro de curva CN, que a su vez, se relaciona con S.

  4. Las estimaciones de CN se basan en: (1) grupo hidrológico de suelo; (2) clases de uso y tratamiento del terreno; (3) condición hidrológica de la superficie; y (4) condición de humedad antecedente.

6.  ECUACIÓN DE LA CURVA DE ESCORRENTÍA

El método asume una proporcionalidad entre retención y escorrentía, como sigue:

Ecuación

   F        Q             
____ = _____  
  S         P        
(3)

en la cual F = P - Q = retención actual; S = retención potencial; Q = escorrentía actual; y P = escorrentía potencial, es decir, precipitación total. Los valores de P, Q y S se dan en dimensiones de profundidad. Si bien el método original se desarrolló en unidades habituales de EE. UU. (pulgadas), es posible una conversión a unidades SI (cm) (Ponce 1989). La precipitación P es la profundidad total de tormenta. La escorrentía Q es la profundidad total de escorrentía directa resultante de la tormenta P. La retención potencial S es la profundidad máxima de tormenta que podría ser extraída potencialmente por un sitio determinado.

Abstracción inicial

En un caso típico, una cierta cantidad de lluvia, conocida como "abstracción inicial", se abstrae como intercepción, infiltración y almacenamiento superficial antes de que comience la escorrentía. En el método del número de la curva, esta abstracción inicial lα se substrae de la precipitación P en la Ec. 3 para dar lo siguiente:

     P - lα - Q             Q             
  ____________  =  _______  
         S                   P - lα        
(4)

Resolviendo para Q en la Ec. 4 se tiene:

              (P - lα)2             
Q =    ____________  
            P - lα + S        
(5)

el cual es válido para P > lα, es decir, después de que comience el escorrentía; y Q = 0 en caso contrario. Con la abstracción inicial incluida en la Ec. 4, la retención actual P - Q se acerca asintóticamente a un valor constante S + lα, a medida que la precipitación crece sin límites.

La Ecuación 5 tiene dos parámetros: S e lα. Para eliminar la necesidad de una estimación independiente de la abstracción inicial, se sugirió una relación lineal entre lα y S [SCS (1985), y versiones anteriores]:

lα  = λS (6)

en la cual λ = relación de abstracción inicial.

La Ecuación 6 se justificó sobre la base de mediciones en cuencas hidrográficas de menos de 10 acres (SCS 1985). Si bien hubo una dispersión considerable en los datos, NEH-4 informó que el 50% de los puntos de datos se encuentran dentro de los límites 0.095 ≤ λ ≤ 0.38 [SCS (1985), y versiones anteriores]. Esto llevó a SCS a adoptar un valor estándar de la relación de abstracción inicial λ = 0.2. Sin embargo, se han documentado valores que varían en el rango 0.0 ≤ λ ≤ 0.3 en varios estudios que abarcan ubicaciones geográficas en los Estados Unidos y otros países ("Estimación" 1972; Springer et. al. 1980; Cozier y Hawkins 1984; Ramasastri y Seth 1985; Bosznay 1989).

Con λ = 0.2 en la Ec. 6, la Ec. 5 se convierte en:

         (P - 0.2S)2             
Q = ____________  
          P + 0.8S        
(7)

sujeta a P > 0.2S; y Q = 0 en caso contrario.

La Ecuación 7 contiene solo un parámetro, la retención potencial S, que varía en el rango 0 ≤ S ≤ ∞. Por conveniencia en aplicaciones prácticas, S se mapea en un parámetro adimensional CN, el llamado número de la curva, el cual varía en un rango más atractivo 100 ≥ CN ≥ 0. La ecuación de mapeo elegida es:

         1,000             
S =  ________ - 10
           CN        
(8)

en la cual 1,000 y 10 son constantes elegidas arbitrariamente, con las mismas unidades que S (pulgadas). Resolviendo para CN:

            1,000             
CN = _________ 
           S + 10        
(9)

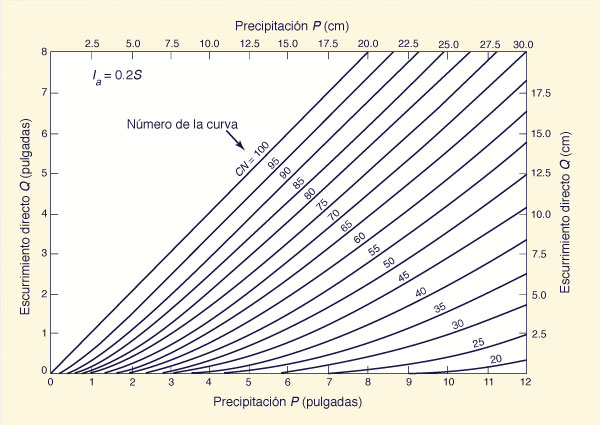
Un CN = 100 representa una condición de retención potencial cero (S = 0), es decir, una cuenca hidrográfica impermeable. Por el contrario, un CN = 0 representa un límite superior teórico para la retención potencial (S = ∞), es decir, una abstracción infinita.

Sustituyendo la Ec. 8 en la Ec. 7, se obtiene la ecuación que relaciona el escorrentía directa Q con la precipitación pluvial P, con CN como número de la curva, o parámetro de curva:

               [CN (P + 2) - 200] 2             
Q =  _________________________ 
            CN [CN (P - 8) + 800]        
(10)

sujeta a P > (200/CN) - 2; y Q = 0 en caso contrario.

La Ecuación 5 se puede expandir para obtener lo siguiente (Chen 1976; Hawkins 1978b):

                                S 2             
Q = P - lα - S +  ___________ 
                           P - lα + S        
(11)

Esta ecuación revela que a medida que el escorrentía potencial crece sin límites (P - lα → ∞), la retención actual, excluyendo la abstracción inicial (P - lα - Q), se aproxima asintóticamente a la retención potencial S. Este es el principio básico del método del número de la curva, es decir, el comportamiento asintótico de la retención actual hacia la retención potencial para valores suficientemente grandes de escorrentía potencial. Hay que tener en cuenta que este comportamiento simula adecuadamente el flujo de saturación de superficie. A este respecto, Chen (1975, 1976, 1982) ha derivado una ecuación de infiltración basada en el método del número de la curva y la ha relacionado con la ecuación de infiltración de Holtan, que toma en cuenta explícitamente el almacenamiento disponible en el suelo (Holtan et. al. 1975).

En la práctica, hay algunas situaciones en las que la relación lluvia de tormenta-escorrentía no sigue estrictamente la Ec. 11. En estos casos, ajustar un número de la curva a partir de los datos puede resultar un desafío (Hawkins 1993). Modelos alternativos de precipitación-escorrentía como el siguiente:

Q = b (P - lα )
(12)

han sido formulados (Fogel y Duckstein 1970; Hawkins 1942), pero el problema subsiste en determinar el coeficiente empírico b, preferiblemente en función de las propiedades productoras de escorrentía. Un aparente inconveniente de la Ec. 12 es que a medida que la escorrentía potencial crece sin límites (P - lα → ∞), la retención actual también crece sin límites (P - lα - Q → ∞), simulando la capacidad de almacenamiento infinito, es decir, retención potencial infinita. Esta misma característica la comparten las clásicas fórmulas de infiltración de Green y Ampt, Horton y Phillip, situación que ha llevado a que se las describa como sin fondo es decir, capaces de simular el flujo Hortoniano de superficie. Por otro lado, el método del número de la curva tiene un valor finito de almacenamiento S para todos los números de curva, excluyendo el caso especial de CN = 0, que es solo un límite teórico y no es usado en la práctica.

Base conceptual

Los comienzos empíricos del método del número de la curva no restan de ninguna manera su clara base conceptual. De hecho, es sólo bajo un marco conceptual que podemos discernir por qué las razones de retención y escorrentía deberían ser iguales (Ec. 3). La igualdad de estas proporciones conduce a un modelo conceptual en el cual el número de la curva es el único parámetro que describe el proceso. A su vez, este parámetro es un substituto de la retención potencial, una medida del almacenamiento subsuperficial disponible, es decir, de la capacidad de un sitio determinado para abstraer la lluvia de tormenta.

7.  CONDICIÓN DE HUMEDAD ANTECEDENTE

Un modelo conceptual funciona en la media, lo que implica que existe espacio para cierta variabilidad. El desarrollo temprano del método del número de la curva confirmó que esta variabilidad era real y que la misma cuenca podía tener más de un número de la curva, es decir, un conjunto de números de curva (SCS 1985; Hjelmfelt 1991). Entre las fuentes probables de esta variabilidad se encuentran:

Humedad antecedente: Componentes

  1. El efecto de la variabilidad espacial de las propiedades de las tormentas y las cuencas hidrográficas,

  2. El efecto de la variabilidad temporal de la tormenta, es decir, la intensidad de la tormenta,

  3. La calidad de los datos medidos, es decir, los datos de P - Q, y

  4. El efecto de las precipitaciones antecedentes y la consiguiente humedad del suelo.

Esto último fue reconocido en forma temprana como la fuente primaria o manejable de la variabilidad y, por lo tanto, llevó al concepto de condición de humedad antecedente (AMC - SCS 1985). Más recientemente, se ha hecho referencia al mismo concepto como la condición antecedente de escorrentía (ARC) para denotar un cambio de énfasis de la humedad del suelo al escorrentía ("Urban" 1986).

Los números de la curva del manual original se desarrollaron a partir de datos registrados de precipitación-escorrentía, dados el grupo hidrológico de suelo, la clase de uso/tratamiento de la tierra y la condición hidrológica de la superficie. En el desarrollo del método se utilizaron datos diarios de precipitación-escorrentía correspondientes a la serie de inundaciones anuales en un sitio (Rallison y Cronshey 1979). Los datos se representaron como precipitación P en las abscisas y escorrentía directa Q en las ordenadas. El CN correspondiente a la curva que separaba la mitad de los datos graficados de la otra mitad se tomó como el número de la curva mediana para el sitio dado. Los valores del CN de las tablas NEH-4 representan el promedio de los valores de CN del sitio medio con el suelo, cobertura y la condición de la superficie indicados. La condición promedio se tomó como la respuesta promedio, que luego se extendió para implicar la condición promedio de humedad del suelo (Miller y Cronshey 1989). La dispersión natural de puntos alrededor de la mediana CN se interpretó como una medida de la variabilidad natural de la humedad del suelo y la relación precipitación-escorrentía asociada.

Para tener en cuenta esta variabilidad, las gráficas P-Q se utilizaron para definir valores de CN envolventes o casi envolventes para cada sitio. Si bien los límites teóricos del número de la curva son CN = 0 (Q = 0) y CN = 100 (Q = P), los valores de CN envolventes reducen los límites a valores prácticos basados en la experiencia. Estos valores de CN envolventes se consideran los límites prácticos superior e inferior de la variabilidad esperada de CN para la combinación dada de suelo-cobertura. Por lo tanto, la condición de humedad antecedente se utilizó como parámetro para representar la observada variabilidad (Rallison y Cronshey 1979).

Número de la curva medio: Condición Antecedente 2

El número de la curva que se encuentra en el medio de la distribución es el número de la curva mediano, correspondiente a AMC 2 (potencial de escorrentía promedio). Éste es el número de la curva estándar que se proporciona en las tablas del SCS (SCS 1985). El valor bajo es el número de la curva seca, de AMC 1 (potencial de escorrentía más bajo); el valor alto es el número de la curva húmeda, de AMC 3 (mayor potencial de escorrentía más alto).

Correlaciones

NEH-4 contiene una tabla de conversión (Tabla 10.1), la cual enumera los valores CN correspondientes de AMC 1 y AMC 3 para los valores de CN de AMC 2 dados. Los valores originales de esta tabla, contenidos en la edición de 1956 de NEH-4, se basaron en datos no modificados. Los valores de la actual tabla de conversión de AMC [en SCS (1985)] se han modificado ajustando líneas rectas en papel de probabilidad normal. Aprovechando este hecho, Sobhani (1975) y Hawkins et. al. (1985) desarrollaron correlaciones entre las retenciones de potencial seco o húmedo S1 y S3 y la retención potencial promedio S. Hawkins et. al. (1985) informó lo siguiente:

S1  = 2.281S2 (13)

con r 2 = 0.999, y Se = 0.206 pulg., y

S3  = 0.427S2 (14)

con r 2 = 0.994, y Se = 0.088 pulg.

Estas ecuaciones son aplicables en el rango 55 ≤ CN ≤ 95, que abarca la mayoría de los números de curva estimados o experimentados.

La sustitución de la Ec. 13 y Ec. 14 en la Ec. 8 conduce a lo siguiente:

                           CN2             
CN1 =  ________________________  
               2.281 - 0.01281 CN2        
(15)

con r 2 = 0.996, y Se = 1.0 CN, y

                           CN2             
CN3 =  _______________________  
              0.427 - 0.00573 CN2        
(16)

con r 2 = 0.994, y Se = 0.7 CN.

La relación biunívoca entre CN y S (Ecs. 8 y 9) hace que este último esté intrínsecamente relacionado con la humedad antecedente. Por lo tanto, la retención potencial es una medida de la capacidad de un sitio determinado para extraer y retener la tormenta, siempre que el nivel de humedad antecedente se haya tenido en cuenta en el análisis. En otras palabras, la retención potencial y su número de la curva correspondiente tienen la intención de reflejar no sólo la capacidad de un sitio dado para extraer y retener la tormenta, sino también lo siguiente: (1) la historia reciente de lluvias antecedentes, o la falta de ellas, que puede haber causado que la humedad del suelo se aparte de un nivel promedio; (2) variaciones estacionales en las propiedades de la escorrentía; y (3) tormentas inusuales.

La humedad del sitio como factor determinante

En esta función, la humedad del sitio actúa per se como un substituto de todas las demás fuentes de variabilidad, más allá de lo que podría atribuirse al suelo, el uso/tratamiento del terreno y la condición hidrológica de la superficie. Hjelmfelt et. al. (1982) encontraron que la tabla de conversión de AMC describía el 90% (AMC 1), 50% (AMC 2) y 10% (AMC 3) de probabilidades acumuladas de excedencia de la profundidad de escorrentía para una tormenta determinada. En otras palabras, encontraron que AMC 2 representaba la tendencia central, mientras que AMC 1 y AMC 3 explicaban la dispersión en los datos. Un análisis similar fue realizado por Gray et. al. (1982), usando datos de Indiana, Kentucky y Tennessee, y por Hawkins (1983), usando datos de Arizona y Utah. Hawkins et. al. (1985), interpretaron las categorías de AMC como "bandas de error" o envolventes que indican la variabilidad experimentada en los datos de precipitación-escorrentía.

¿Qué nivel de AMC se debe utilizar en un caso determinado? Para este propósito, NEH-4 (SCS 1985) muestra el nivel apropiado de AMC basado en el total de precipitación antecedente de 5 días, para la temporada de inactividad y crecimiento (Tabla 4.2: "Límites de precipitación estacional para AMC"). Esta tabla se desarrolló utilizando datos de una ubicación no especificada y posteriormente se adoptó para uso general (Miller y Cronshey 1989). Desafortunadamente, la tabla no tiene en cuenta las diferencias regionales o los efectos de escala. Es probable que se requiera un período antecedente superior a 5 días para cuencas hidrográficas más grandes. Haciendo eco de esta limitación, SCS ha eliminado más recientemente la Tabla 4.2 de la nueva versión del Capítulo 4, NEH-4, publicada en 1993.

En la práctica, la determinación de AMC se deja al usuario, quien debe evaluar si una determinada situación de diseño justifica AMC 1, AMC 2 o AMC 3. Se entiende que AMC 2 representa una situación de diseño típica. Una elección de AMC 1 da como resultado un menor volumen de escorrentía, mientras que un mayor escorrentía resulta de una elección de AMC 3. Los manuales de diseño especifican la elección de AMC en función del período de retorno, con el nivel de AMC aumentando con el período de retorno. Por ejemplo, el Manual de Hidrología (1986) del condado de Orange, California, especifica AMC 1 para tormentas de 2 y 5 años, AMC 2 para tormentas de 10, 25 y 50 años y AMC 3 para tormentas de 100 años . Asimismo, el Manual de Hidrología (1985) del Condado de San Diego. California, especifica valores de AMC que varían entre 1.5 y 3.0 (en incrementos de 0.5) para un rango de frecuencias de diseño (5-150 años) y cuatro regiones climáticas: costa. estribaciones, montañas y desierto. Si bien SCS no respalda el uso de niveles fraccionales de AMC (Rallison y Cronshey 1979), la práctica existe y debe reconocerse.

8.   NÚMEROS DE LA CURVA EVALUADOS A PARTIR DE LOS DATOS

Desde el inicio del método, varios investigadores han intentado determinar los números de la curva a partir de los datos de precipitación y escorrentía de cuencas pequeñas. El objetivo ha sido verificar los valores de CN dados en las tablas estándar, o extender la metodología a otras cobertura de suelo y ubicaciones geográficas no contempladas en el manual NEH-4. Un procedimiento establecido resuelve S en la Ec. 7, que conduce a (Hawkins 1973; 1979):

Evaluación basada en datos de P y Q

S  = 5 [P + 2Q - (4 Q 2 + 5 PQ )1/2] (17)

Para un par P y Q dado, la retención potencial S se calcula con esta ecuación, y el correspondiente CN es calculado con la Ec. 9.

Hay varias formas de seleccionar los pares P-Q para el análisis. El método estándar, denominada serie de inundaciones anuales, es seleccionar la precipitación diaria P y su correspondiente volumen de escorrentía Q (ambos en pulgadas) para las inundaciones anuales en un sitio (Rallison y Cronshey 1979; Springer et. al. 1980). Este procedimiento tiene la ventaja de que da como resultado un rango considerable en los valores de precipitación y escorrentía. Las desventajas percibidas son las siguientes: (1) este tipo de datos no está disponible fácilmente; (2) los períodos de retorno de los correspondientes eventos de precipitación y escorrentía no son necesariamente los mismos; y (3) solo hay un dato por año de medición.

Eventos participantes

En ausencia de una serie extensa de inundaciones anuales, particularmente en las regiones semiáridas, algunos investigadores han optado por utilizar criterios menos selectivos para posibles eventos de tormenta, incluidos los eventos de período de retorno menores de un año (Woodward 1973; Hawkins 1984). Esta elección da como resultado mucho más datos para el análisis, así como valores de CN ligeramente diferentes en comparación con los obtenidos utilizando una serie de avenidas anuales (Springer et. al. 1980). La elección de la frecuencia de los posibles eventos de tormentas es objeto de continua investigación (Woodward y Gburek 1992).

Otro enfoque para determinar los números de la curva a partir de datos es el método de emparejamiento de frecuencias (Hjelmfelt 1980). La tormenta y las profundidades de escorrentía directa se clasifican por separado y luego se realinean según el orden de clasificación para formar pares P-Q aparentemente deseables de período de retorno igual. Sin embargo, los valores de escorrentía individuales no están necesariamente asociados con los causales valores de precipitación (Hawkins 1993).

9.   OTRAS EXPRESIONES DE LA ECUACIÓN DEL NÚMERO DE LA CURVA

El número de la curva de escorrentía SCS se ha aplicado en muchos países del mundo. Por lo tanto, su expresión en unidades SI es necesaria. Asimismo, las diferencias geográficas y de otro tipo pueden dictar que el índice de abstracción inicial λ se amplie al rango validado por la experiencia local, digamos 0.0 ≤ λ ≤ 0.3.

Otras expresiones

En unidades SI, Ec. 10 se convierte en los siguiente:

            R {CN [(P/R) + 2] - 200}2             
Q  =  ___________________________  
           CN {CN [(P/R) - 8] + 800}    
(18)

en la cual P (cm) se divide por R = 2.54 (cm/pulg), y el resultado del cálculo se multiplica por R, para dar Q en cm. Al ser adimensional, el número de la curva CN sigue siendo el mismo tanto en unidades SI como habituales de EE. UU. La Ec. 18 está sujeta a la restricción P > R [(200/CN) - 2]; y Q = 0 en caso contrario.

Para obtener la ecuación numérica de la curva de escorrentía para una variable λ, las Ecs. 6 y 8 se sustituyen en la Ec. 5 para obtener (Ponce 1989):

                     [CN (P + 10λ) - 1,000λ]2             
Q  =  ______________________________________  
          CN {CN [(P - 10(1 - λ)] + 1,000(1 - λ)}    
(19)

la cual está sujeta a la restricción P > (1,000 λ/ CN) - 10λ; y Q = 0 en caso contrario.

La Ecuación 17 es aplicable solo para el valor estándar de abstracción inicial λ = 0.2. Para λ = 0:

S  = (P/Q) (P - Q)
(20)

En general, para λ > 0 (Chen 1982):

S  = (λ-1) {P + (0.5λ-1) [(1 - λ) Q - [(1 - λ)2Q 2 + 4λ PQ ]1/2 ]}
(21)

10.  CRÍTICA DEL NÚMERO DE LA CURVA

Existe una creciente literatura sobre el método del número de la curva (Bosznay 1989; Hjelmfelt 1991; Hawkins 1993; Steenhuis et. al. 1995). Bastará aquí enumerar las ventajas y desventajas del método. Las ventajas son:

Ventajas

  1. Es un método conceptual simple, predecible y estable para la estimación de la profundidad de escorrentía directa basado en la profundidad de la tormenta, respaldado por datos empíricos.

  2. Se basa en un solo parámetro, el número de la curva CN, que varía en función de cuatro propiedades principales de la cuenca productora:

    • Grupo hidrológico de suelos: A, B, C y D,

    • Clases de uso y tratamiento del terreno: agrícola, de pastoreo, forestal y, más recientemente, urbano ("Urban" 1986),

    • Condición hidrológica de la superficie de los pastos nativos: pobre, regular y bueno, y

    • Condición de humedad antecedente, un substituto de otras fuentes de variabilidad, incluida la humedad del suelo: 1, 2 y 3.

  3. Es la única metodología gubernamental que presenta insumos ambientales de fácil comprensión y razonablemente bien documentados (suelo, uso/tratamiento del terreno, condición hidrólogica de la superficie y condición de humedad antecedente).

  4. Es un método bien establecido, que ha sido ampliamente aceptado para su uso en Estados Unidos y otros países.

Si bien es teóricamente posible que sus números abarquen el rango de 0 a 100, es más probable que los valores de diseño práctico validados por la experiencia estén en el rango de 40 a 98, con algunas excepciones (Van Mullem 1989). Esta es una ventaja considerable, porque restringe el único parámetro del método a un rango relativamente estrecho. Visto desde esta perspectiva, se ve que la estimación de un CN de diseño es de hecho un ejercicio empírico dentro de un marco conceptual. Tal ejercicio no es diferente al de estimar la C de Chezy o la n de Manning en el flujo en canales (Hawkins 1975).

Desventajas

Las desventajas percibidas del método CN son:

  1. El método se desarrolló originalmente utilizando datos regionales, principalmente del medio oeste de los Estados Unidos, y desde entonces se ha extendido mediante la práctica a todo los Estados Unidos y otros países. Se recomienda cierta precaución para su uso en otras regiones geográficas o climáticas. Los estudios locales y la experiencia deben substituirse por las tablas de CN a nivel nacional de EE.UU. cuando se considere apropiado.

  2. En algunos casos, particularmente para los números de curva y/o profundidades de precipitación más bajos, el método puede ser muy sensible al número de la curva y la condición de humedad antecedente (Hawkins 1975; Bondelid et. al. 1982; Ponce 1989). Éste no es necesariamente un punto débil, ya que puede ser un reflejo de la variabilidad natural; sin embargo, existe una falta de orientación clara sobre cómo variar la condición de humedad antecedente.

  3. El método funciona mejor en zonas agrícolas, para el cual fue diseñado originalmente. Desde entonces, su aplicabilidad se ha extendido a sitios urbanos ("Urban" 1986). El método es bastante apropiado para aplicaciones en pastizales y, en general, no es bueno para aplicaciones en bosques (Hawkins 1984, 1993). La implicación es que el número de la curva (desarrollado por SCS) es más adecuado para las estimaciones de escorrentía pluvial de tormentas en corrientes con flujo base insignificante, es decir, aquéllos para los cuales la relación de escorrentía directa a escorrentía total es cercana a uno. Típicamente, éste es el caso de corrientes de primer y segundo orden en regiones subhúmedas y húmedas, y de corrientes efímeras en regiones áridas y semiáridas.

  4. El método no tiene una provisión explícita para tomar en cuenta los efectos de escala espacial. Por ejemplo, Simanton et. al. (1973) han demostrado que el número de la curva para áreas de menos de 560 acres (227 ha) en el sureste de Arizona tiende a disminuir con el aumento del tamaño de la cuenca, lo que refleja el papel importante de las pérdidas por transmisión en los canales en esta región semiárida. En ausencia de pautas claras, se supone que el número de la curva se aplica a cuencas de captación pequeñas y medianas, comparables en tamaño a las que normalmente caen dentro del alcance de SCS. Sin la subdivisión de la cuenca y el enrutamiento del flujo asociado, su aplicación a grandes cuencas (más de 100 millas cuadradas o 250 kilómetros cuadrados) debe hacerse con precaución.

  5. El método fija la tasa de abstracción inicial en λ = 0.2. Al principio, esto parece ser una ventaja, ya que reduce efectivamente el número de parámetros a uno. Sin embargo, en general, λ podría interpretarse como un parámetro regional para mejorar la capacidad de respuesta del método a una diversidad de entornos geológicos y climáticos (Bosznay 1989; Ramasastri y Seth 1985). Es necesario mayor investigación para arrojar luz sobre este tema.

11.  NÚMERO DE LA CURVA: ¿HA ALCANZADO LA MADUREZ?

Habiendo revisado sus fundamentos, su base conceptual/empírica y su rango de aplicabilidad, ahora se aborda el tema central de este artículo: ¿El método del número de la curva ha alcanzado la madurez? Madurez implica utilidad, aceptación con defectos reconocidos, comprensión de sus capacidades y crecimiento continuo con posibles refinamientos eventuales.

Consideraciones finales

Se considera que el método ha alcanzado la madurez debido a lo siguiente:

  1. El método es ampliamente entendido y aceptado por lo que es: Un modelo conceptual respaldado con datos empíricos para estimar el volumen de escorrentía directa, basado en la profundidad de tormentas poco frecuentes, agrupado para evitar la descripción, a menudo engorrosa, de la variabilidad espacial y temporal de infiltración y otras pérdidas.

  2. Es el método elegido por los ingenieros e hidrólogos para la planificación y el diseño de la conservación de suelos y agua, y el diseño de obras para el control de inundaciones. El método está contenido en la mayoría de los modelos hidrológicos de uso actual, en los Estados Unidos y en otros países. Su practicalidad como método de diseño está fuera de toda duda.

  3. Un método de reemplazo, si se desarrollara, tendría que demostrar claramente su superioridad. Ninguna de las fórmulas de infiltración existentes, como las de Horton, Philip o Green y Ampt, es irreprochable. Una aparente limitación es que permiten una cantidad infinita de almacenamiento de humedad en el suelo. Más importante, sin embargo, es la crítica de que ninguno de estos métodos puede reclamar un enfoque holístico, es decir, uno que tome en cuenta los aspectos físicos, químicos y biológicos, y que incluya todos los procesos importantes. En muchos casos, los aspectos biológicos de la infiltración pueden estar sujetos a tal diversidad espacial (el efecto de las características vegetativas del subsuelo, como raíces y descomposición de raíces, y macro y microfauna) que desafían la descripción hasta por los modelos más complejos.

12.  RESUMEN

El método del número de la curva de escorrentía debe su popularidad entre los profesionales de la hidrología a su simplicidad, reproducibilidad y estabilidad, y el respaldo de una importante agencia federal de los Estados Unidos. En las siete décadas que han transcurrido desde sus inicios, han surgido interrogantes sobre su naturaleza y sus orígenes. Su adopción y uso en los Estados Unidos y otros países a nivel mundial, más allá del alcance previsto por sus desarrolladores originales, ha requerido que el método sea sujeto a un minucioso escrutinio.

Conclusiones

El método es un modelo conceptual de abstracción hidrológica de tormentas, respaldado por datos empíricos. Su objetivo es estimar el volumen de escorrentía directa a partir de la profundidad de la tormenta, basado en un número de la curva CN. Este número, el cual varía en el rango conveniente 100 ≥ CN ≥ 0, es un substituto de la retención potencial, un parámetro conceptual que varía en el rango 0 ≤ S ≤ ∞. [En la práctica: 100 ≥ CN ≥ 1, lo que equivale a 0 ≤ S ≤ 990 pulgadas, este último un valor considerado muy grande].

El método no tiene en cuenta la variabilidad espacial y temporal de la infiltración y otras pérdidas; más bien, los agrega en un cálculo de la pérdida de profundidad total para una tormenta y una cuenca dadas. El método describe tendencias medias, lo cual le impide ser perfectamente predictivo. La variabilidad observada en los números de la curva, más allá de la que se puede atribuir al tipo de suelo, uso/tratamiento del terreno y condición hidrológica de la superficie, está incorporada en el concepto de condición de humedad antecedente.

Las ventajas del método son: (1) simplicidad; (2) reproducibilidad; (3) estabilidad; (4) dependencia de un solo parámetro; y (5) capacidad de respuesta a las principales propiedades de las cuencas. Las desventajas son: (1) marcada sensibilidad a la elección del número de la curva; (2) ausencia de una guía clara sobre cómo variar la condición de humedad antecedente; (3) precisión variable del método para diferentes biomas; (4) ausencia de una manera explícita para tomar en cuenta los efectos de escala espacial; y (5) fijación de la tasa de abstracción inicial en λ = 0.2, desalentando una posible regionalización basada en el entorno geológico y climático.

APÉNDICE I.  BIBILOGRAFÍA

  1. Aron G., A. C. Miller, y D. F. Lakatos. 1977. "Infiltration formula based on SCS curve number." J. Irrig. y Drain. Div., ASCE, 103(4),419-427. 419-427.

  2. Bondelid, T. R., R. H. McCuen, y T. J. Jackson. 1982. "Sensitivity of SCS models to curve number variation." Water Resour. Bull., 18(1), 111-116. 111-116.

  3. Bosznay, M. 1989. "Generalization of SCS curve number method." J. Irrig. y Drain. Engrg., ASCE, 115(1), 139-144.

  4. Boughton, W. C. 1989. "A review of the USDA SCS curve number method." Aust. J. Soil Res., 27 , 511-523.

  5. Branson, F. A., G. F. Gifford, K. G. Renard, y R. F. Hadley. 1981. Rangeland hydrology. Society for Range Management, Range Science. Series No. 1, Kendall/Hunt Publ. Co., Dubuque, Iowa.

  6. Branson, F. A., R. F. Miller, y I. S. Queen. 1962. "Effects of contour furrowing, grazing intensities, and soils on infiltration rates, soil moisture and vegetation near Fort Peck, Montana." J. Range Mgmt., 15, 151-158.

  7. Cazier, D. J., y R. H. Hawkins. 1984. "Regional application of the curve number method." Water Today and Tomorrow, Proc., ASCE Irig. and Drain. Div. Spec. Conf ., ASCE, New York, N.Y.

  8. Chen, C. L. 1975. "Urban storm runoff inlet hydrograph study." Vol. 5. Soil-cover-moisture complex: Analysis of parametric infiltration models for highway sideslopes. Report PRWG106-5, Utah Water Research Laboratory, Utah State Univ., Logan, Utah.

  9. Chen, C.L. 1976. "Urban storm runoff inlet hydrograph study." Vol.5, Soil-cover-moisture complex: Analysis of parametric infiltration models for highway sideslopes. Report FHWA-RD-76-120, Federal Highway Administration (FHwA), Washington, D.C.

  10. Chen, C.-L. 1982. "An evaluation of the mathematics and physical significance of the Soil Conservation Service curve number procedure for estimating runoff volume." Proc., Int. Symp. on Rainfall-Runoff Modeling, Water Resources Publ., Littleton, Colo., 387-418.

  11. Chorley, R. J. 1978. "Chapter 1: The hillslope hydrologic cycle." Hillslope hydrology, M. J. Kirkby, ed., John Wiley and Sons. New York. N.Y.

  12. Dooge, J. C. I. 1977. "Problems and methods of rainfall-runoff modeling." Mathematical models for surface water hydrology, John Wiley and Sons, New York, N.Y.

  13. "Estimation of direct runoff from rainfall." Handbook of Hydrology, Chapter 5. Ministry of Agriculture, Government of India.

  14. Fogel, M. M., y L. Duckstein. 1970. "Prediction of convective storm runoff in semiarid regions." Proc., IASH-Unesco Symp. on the results of research on representative and experimental basins, Wellington, New Zealand,

  15. Gray, D.D., P. G. Katz, S. M. deMonsabert, y N.P. Cogo. 1982. "Antecedent moisture condition probabilities." J. Irrig. and Drain. Div., ASCE, 108(2), 107-114.

  16. Green, W. H., y G. A. Ampt. 1911. "Studies of soil physics. 1. The flow of air and water through soils." J. Agric. Soils, 4, 1-24.

  17. Hawkins, R. H. 1973. "Improved prediction of storm runoff from mountain water sheds." J. Irrig. and Drain. Div., ASCE, 99(4), 519-523.

  18. Hawkins, R. H. 1975. "The importance of accurate curve numbers in the estimation of storm runoff." Water Resour. Bull., 11(5), 887-891.

  19. Hawkins, R. H. 1978a. "Effects of rainfall intensity on runoff curve numbers." Proc., 1978 Meeting of the Arizona Section of the Am. Water Resour. Assoc., Flagstaff, Ariz., 53-64.

  20. Hawkins, R. H. 1978b. "Discussion to 'Infiltration formula based on SCS curve number.'" J. Irrig. and Drain. Engrg., ASCE, 104(4), 464-467.

  21. Hawkins, R. H. 1979. "Runoff curve numbers from partial area watersheds." J. Irrig. and Drain. Div., ASCE. 105(4). 375-389.

  22. Hawkins, R. H. 1980. "Infiltration and curve numbers: Some pragmatic and theoretical relationships." Proc., ASCE Irrig. and Drain. Div. Symp. on Watershed Mgmt., ASCE, New York, N.Y., Vol. II, 925-937.

  23. Hawkins, R. H. 1981. "Interpretations of source area variability in rainfall-runoff relations." Proc., Int. Symp. on Rainfall-Runoff Modeling, Water Resour. Publ., Littleton, Colo., 303-324.

  24. Hawkins, R. H. 1982. "Loss rate distribution implicit in the SCS runoff equation." Proc., Joint Meeting of the Arizona-Nevada Academy of Sci. and Arizona Section, Am. Water Resour. Assoc.

  25. Hawkins, R. H. 1983. "Discussion of 'Antecedent moisture condition probabilities.'" J. Irrig. and Drain. Engrg., ASCE, 109(2), 298-299.

  26. Hawkins, R. H. 1984. "A comparison of predicted and observed runoff curve numbers." Proc., Spec. Conf., Irrig. and Drain. Div., ASCE, New York, N.Y., 702-709.

  27. Hawkins, R. H., A. T. Hjelmfelt, y A. W. Zevenberger. 1985. "Runoff probability, storm depth, and curve numbers." J. Irrig. and Drain. Engrg., ASCE, 111(4), 330-340.

  28. Hawkins, R. H. 1992. "Variety, classification, and association in runoff response." Rep., School of Renewable Natural Resour., Univ. of Arizona, Tucson, Ariz., Nov.

  29. Hawkins, R. H. 1993. "Asymptotic determination of runoff curve numbers from data." J. Irrig. and Drain. Engrg., ASCE, 119(2), 334-345.

  30. Hawkins, R. H., y T. W. Cundy. 1982. "Distribution of loss rates implicit in the SCS runoff equation." Proc., Colorado State Univ. Hydrol. Days, Fort Collins, Colo.

  31. Hjelmfelt, A. T. Jr. 1980. "Empirical investigation of curve number technique." J. Hydr. Div., ASCE. 106(9), 1471-1477.

  32. Hjelmfelt, A. T. 1991. "Investigation of curve number procedure." J. Hydr. Engrg., ASCE, 117(6), 725-737.

  33. Hjelmfelt, A. T. Jr., K. A. Kramer, y R. E. Burwell. 1982. "Curve numbers as random variables." Proc., Int. Symp. on Rainfall-Runoff Modeling, Water Resour. Publ., Littleton, Colo., 365-373.

  34. Holtan, H. N., G. J. Stitner, W. H. Henson, y N. C. Lopez. 1975. "USDAHL-74, revised model of watershed hydrology." Tech. Bull. No. 1518, USDA Agricultural Research Service, Washington, D.C.

  35. Horton, R. E. 1933. "The role of infiltration in the hydrologic cycle." Trans., Am. Geophysical Union, 14, 446-460.

  36. Huber, W. C., J. P. Heaney, B. P. Bedient, y J. P. Bender. 1976. "Environmental resources management studies in the Kissimmee River Basin." Rep. No. ENV-05-76-3, Dept. of Envir. Engrg. Sci., Univ. of Florida, Gainesville, Fla., May.

  37. Hydrology guide for use in watershed planning. 1954. Soil Conservation Service, USDA, Washington, D.C.

  38. Hydrology Manual. 1985. County of San Diego, Calif., Jan.

  39. Hydrology Manual. 1986. Orange County Environmental Management Agency, Calif., Oct.

  40. "Influences of vegetation and watershed treatment on runoff, silting, and streamflow." 1940. Misc. Pub. No. 397, USDA, Washington, D.C.

  41. Kirkby, M. J., y R. J. Chorley. 1967. "Throughflow, overland flow, and erosion." Bull., Int. Assoc. on Sci. Hydrol., 12, 5-21.

  42. Knisel, W. G. 1980. "CREAMS. A field-scale model for chemicals, runoff, and erosion from agricultural management systems." Conservation Rep. No. 26, USDA Agricultural Research Service. Washington, D.C.

  43. Le Bissonnais, Y., y M.J. Singer. 1993. "Seal formation, runoff, and interriill erosion from seventeen California soils." Soil Sci. Soc. of Am. J., 57, 224-229.

  44. Miller, N., y R. Cronshey. 1989. "Runoff curve numbers, the next step." Proc., Int. Conf. on Channel Flow and Catchment Runoff, Univ. of Virginia, Charlottesville, Va.

  45. Mockus, V. 1949. "Estimation of total (and peak rates of) surface runoff for individual storms." Interim Survey Rep. Grand (Neosho) River Watershed, Exhibit A in Appendix B, U.S. Department of Agriculture, Washington, D.C.

  46. Philip, I. R. 1957. "The theory of infiltration." Soil Sci., 83,345-357, 435-458.

  47. Ponce, V. M. 1989. Engineering hydrology, principles and practices. Prentice Hall, Englewood Cliffs, N.J.

  48. Ponce, V. M., y A. V. Shetty. 1995. "A conceptual model of catchment water balance: 1. Formulation and calibration." J. Hydrol., 166.

  49. Rallison, R. E. 1980. "Origin and evolution of the SCS runoff equation." Proc., ASCE Irrig. and Drain. Div. Symp. on Watershed Mgmt., ASCE, New York, N.Y., Vol. II, 912-924.

  50. Rallison, R. E., y R. C. Cronshey. 1979. "Discussion to 'Runoff curve numbers with varying soil moisture.'" J. Irrig. and Drain. Div., ASCE, 105(4), 439-441.

  51. Rallison, R. E., y N. Miller. 1982. "Past, present, and future SCS runoff procedure." Proc., Int. Symp. on Rainfall-Runoff Modeling, Water Resour. Publ., Littleton, Colo., 353-364.

  52. Ramasastri, K. S., y S. M. Seth. 1985. "Rainfall-runoff relationships." Report RN-20, National Institute of Hydrology, Roorkee, Uttar Pradesh, India.

  53. Savabi, M. R., W. I. Rawls, y J. R. Simanton. 1990. "Rangeland evaluation of WEPP hydrology." Proc., ASCE !Mg. and Drain. Div. Symp. on Watershed Mgmt., ASCE, New York, N.Y., 77-87.

  54. SCS National Engineering Handbook. 1985. "Section 4: Hydrology." Soil Conservation Service, USDA, Washington, D.C.

  55. SCS National Engineering Handbook. 1993. "Section 4: Hydrology, Chapter 4." Soil Conservation Service, USDA, Washington, D.C.

  56. Sherman, L. K. 1942. "Hydrographs of runoff." Physics of the Earth, IX, Hydrology, O. E. Meinzer, ed., McGraw-Hill, New York, N.Y.

  57. Sherman, L. K. 1949. "The unit hydrograph method." Physics of the Earth, O. E. Meinzer, ed., Dover Publications, Inc., New York, N.Y., 514-525.

  58. Simanton, J. R., K. G. Renard, y N. G. Sutter. 1973. "Procedures for identifying parameters affecting storm runoff volumes in a semiarid environment." Report W-1, USDA Agricultural Research Service, Washington, D.C.

  59. Smith, R. E. 1976. "Approximations for vertical infiltration rate." Trans., ASAE, 19, 505-509.

  60. Smith, R. E., y K. G. Eggert. 1978. "Discussion to 'Infiltration formula based on SCS curve number.' by G. Aron, A. C. Miller, and D. F. Lakatos." J. Irrig. and Drain. Div., ASCE, 104(4), 462-463.

  61. Sobhani, G. 1975. "A review of selected small watershed design methods for possible adoption to Iranian conditions." M.S. thesis, Utah State Univ., Logan, Utah.

  62. Soni, B., y G. C. Mishra. 1985. "Soil water accouting using SCS hydrologic soil classification." Rep. CS-15, Nat. Inst. of Hydrol., Roorkee, U.P., India.

  63. Springer, E. P., B. J. McGurk, R. H. Hawkins, y G. B. Coltharp. 1980. "Curve numbers from watershed data." Proc., ASCE Irrig. and Drain. Symp. on Watershed Mgmt., ASCE, New York, N.Y., Vol. II, 938-950.

  64. Steenhuis, T. S., M. Winchell, J. Rossing, J. Zollweg, y M. F. Walter. 1995. "SCS runoff equation revisited for variable-source runoff areas." J. Irrig. and Drain. Engrg., ASCE, 121(3), 234-238.

  65. "Urban Hydrology For Small Watersheds." 1986. Technical Release No. 55, Soil Conservation Service, USDA, Washington, D.C.

  66. Van Mullem, J. A. 1989. "Runoff and peak discharges using Green-Ampt infiltration model." J. Hydr. Engrg., ASCE, 117(3), 354-370.

  67. Williams, J. R., y W. V. LaSeur. 1976. "Water yield model using SCS curve numbers." J. Hydr. Div., ASCE, 102(9), 1241-1253.

  68. Woodward, D. E. 1973. "Runoff curve numbers for semiarid range and forest conditions." Proc., Annual Meeting, American Society of Agricultural Engineers, St. Joseph, Mich.

  69. Woodward, D. E. 1991. "Progress report ARS/SCS runoff curve number work group." Proc., Int. Winter Meeting, American Society of Agricultural Engineers, St. Joseph, Mich.

  70. Woodward, D. E., y W. J. Gburek. 1992. "Progress report ARS/SCS runoff curve number work group." Proc., ASCE Water Forum, '92, ASCE, New York, N.Y., 378-382.

APÉNDICE II.  NOTACIÓN

     En este documento se utilizan los siguientes símbolos:

b = exponente en la Ec. 2, coeficiente en la Ec. 12;

CN = número de la curva;

CN1 = número de la curva, seca (AMC 1);

CN2 = número de la curva, promedio (AMC 2);

CN3 = número de la curva, húmeda (AMC 3);

F = retención actual;

Iα = abstracción inicial;

L = pérdidas por abstracción;

P = precipitación, escorrentía potencial;

P - Q = retención actual;

Q = escorrentía, escorrentía actual;

R = factor de conversión de unidades;

r = coeficiente de correlación;

S = retención potencial;

S1 = retención de potencial, seco;

S2 = retención potencial, promedio;

S3 = retención de potencial, húmedo;

Se = error estándar; y

λ = tasa de abstracción inicial.

241004 2130