1. PROBLEM STATEMENT
The maximum discharge in a circular culvert occurs, not when the culvert
is full, but when the culvert is nearly full.
The reason for this is that beyond a certain
relative depth y/D, where y is the flow depth and D is the culvert diameter,
a further increase in depth will make the wetted perimeter
grow faster than the flow area, triggering a decrease in discharge.
In this article, the relative depth y/D which corresponds to
maximum discharge in circular culvert flow is calculated.
2. DERIVATION
According to the Manning equation, the discharge in SI units is (Ponce, 2014):
in which Q = discharge, A = flow area, R = hydraulic radius, S = bottom slope, and n = Manning's n.
Since R = A/P, it follows that:
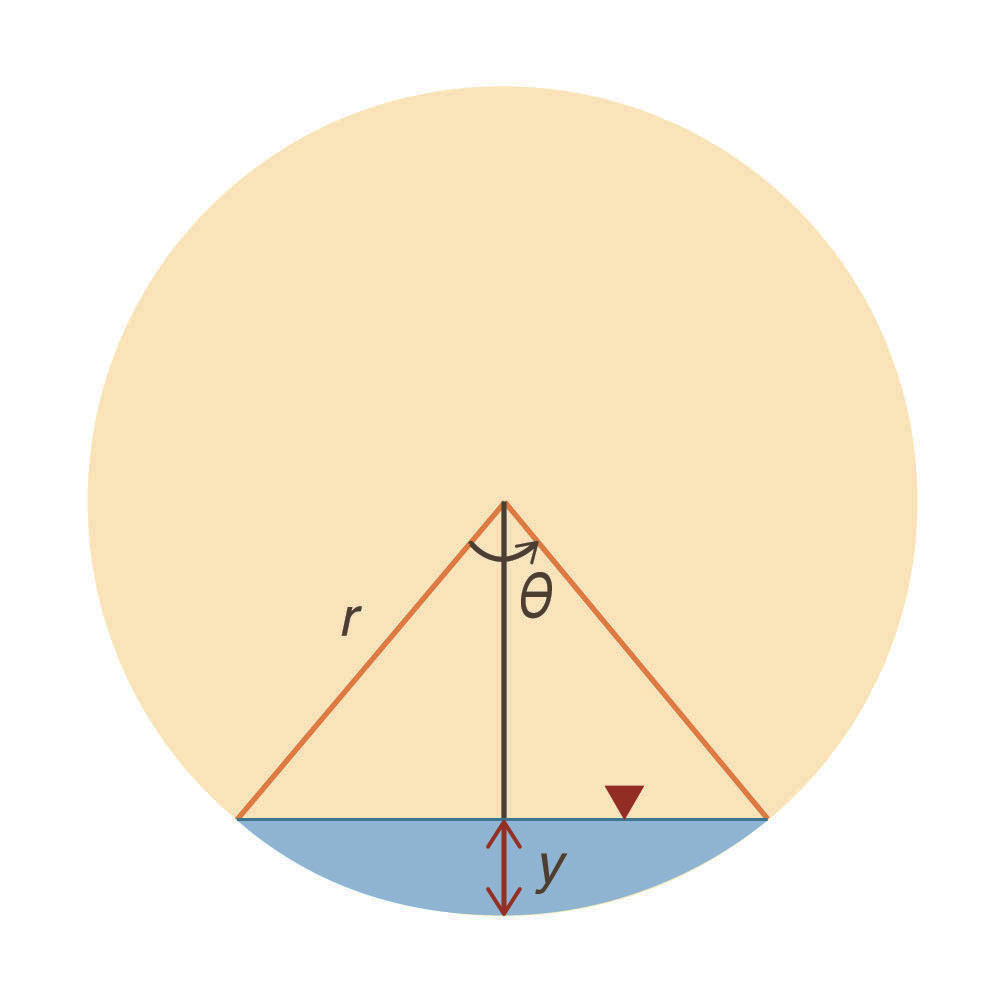
In terms of r and θ, the flow area and wetted perimeter are, respectively (Fig. 1):
Fig. 1 Definition sketch. Therefore:
By geometry, the relative depth is (Fig. 1):
Following differential calculus,
the maximum discharge occurs when dQ/dθ = 0.
Operating on the derivatives:
Simplifying:
Replacing Equations 3 to 6 into Equation 10 and simplifying:
Simplifying Eq. 11:
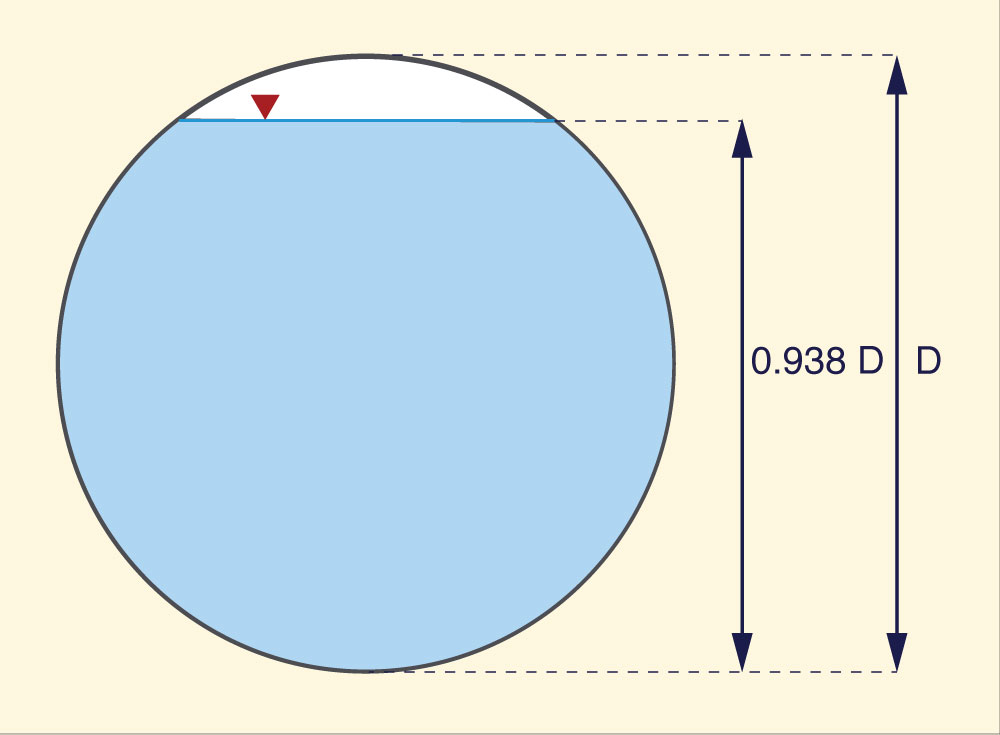
Solving for θ in Eq.10: θ = 302° 25' 51.96". This angle is used in Eq. 7 to solve for relative depth, to give y/D = 0.938 (Fig. 2).
Fig. 2 Relative depth for maximum discharge in a circular culvert..
3. SUMMARY
The relative depth y/D required to achieve maximum discharge
in a circular culvert has been derived using differential calculus. This value is shown to be: y/D = 0.938.
REFERENCE
Ponce, V. M. 2014. Fundamentals of open-channel hydraulics. Online text.
|
| 201223 |