El número de Vedernikov calculado en línea

Víctor M. Ponce

Universidad Estatal de San Diego, California, EE.UU.
vponce@sdsu.edu, poncevm@gmail.com


RESUMEN

Se revisa, explica y aclara el concepto del número de Vedernikov de la hidráulica de canales. Junto con el número de Froude, constituyen una dualidad inseparable, más ahora que su relación con β, el exponente de la curva de gasto (V/F = β - 1), ha sido claramente establecida y su utilidad en el diseño de canales ampliamente documentada. El uso de una calculadora en línea para β y V en términos de variables hidráulicas reconocidas aumenta la utilidad de la teoría, haciendo posible el evitar las ondas de rollo desde la etapa de diseño.

1.  Introducción

El número de Vedernikov es uno de cuatro números adimensionales usados en la hidráulica de canales. Dos de estos números, los números de Froude y Vedernikov, son relaciones de velocidades; los otros dos, el número de Reynolds y el número de onda adimensional de Ponce y Simons, son relaciones de difusividades. Éstos son los únicos números adimensionales que pueden formularse con las tres velocidades y las tres difusividades identificadas por Ponce (1979). Un artículo reciente ha arrojado luz adicional sobre estos conceptos fundamentales (Ponce, 2023a).

Los números de Froude y Reynolds están bien establecidos desde hace más de un siglo (Chow, 1959). Desafortunadamente, el reconocimiento del número de Vedernikov como tal no se ha producido en este período. Esto puede atribuirse al hecho de que Chow optó por mencionar el número de Vedernikov sólo una vez en su reconocido libro de texto "Open-Channel Hydraulics", al final del Capítulo 8, titulado "Conceptos teóricos de capa límite, rugosidad superficial, distribución de velocidades e inestabilidad del flujo uniforme". La experiencia demuestra que solamente algunos ingenieros hidráulicos en ejercicio han leído el Capítulo 8 en su totalidad, relegando el número de Vedernikov a la relativa oscuridad que ha experimentado durante el último medio siglo.

Ponce (1991a) ha presentado los números de Froude (F) y Vedernikov (V) como esencialmente dos partes de la misma narrativa, argumentando en forma convincente a favor de su tratamiento conjunto, algo que Chow (1959) había omitido. En la hidráulica de canales, los dos números constituyen una verdadera dualidad, porque su relación V/F es igual a (β - 1), en el cual β es el exponente de la curva de gasto Q = αAβ. El valor de β es sumamente importante porque encapsula no sólo los números de Froude y Vedernikov, sino también la fricción de fondo y la forma de la sección transversal. Estas proposiciones serán ahora fundamentadas.

2.  El Número de Vedernikov

Para describir apropiadamente el número de Vedernikov, primero hay que definir tres velocidades características en el flujo en canales: (1) la velocidad media del flujo permanente u, (2) la celeridad relativa de las ondas cinemáticas v, y (3) la celeridad relativa de las ondas dinámicas w. Celeridad es la velocidad de una onda, a diferencia de la velocidad media del flujo permanente. Las ondas cinemáticas son las ondas "largas" de Seddon (1900); las ondas dinámicas son las ondas "cortas" de Lagrange (1788).

El número de Froude se define como F = u/w, la relación entre la velocidad media del flujo permanente y la celeridad relativa de la onda dinámica. El valor del umbral F = 1, denominado flujo crítico, separa el flujo subcrítico (F < 1) del flujo supercrítico (F > 1). En un flujo crítico, la propagación de ondas superficiales cortas cambia de flujo en dirección aguas arriba (F < 1) a flujo aguas abajo (F > 1). El número de Froude se utiliza normalmente para describir el flujo permanente; sin embargo, su definición (u/w) revela que también describe el flujo no permanente, aunque sólo las ondas dinámicas (Ponce, 2023b).

El número de Vedernikov se define como V = v /w, la relación entre la celeridad relativa de la onda cinemática y la celeridad relativa de la onda dinámica. El valor del umbral V = 1, denominado flujo neutralmente estable, o flujo neutro, separa el flujo estable (V < 1) del inestable (V > 1). En flujo neutralmente estable, las ondas cinemáticas y dinámicas viajan con la misma celeridad. En flujo estable, las ondas dinámicas viajan más rápido que las ondas cinemáticas. En flujo inestable, las ondas cinemáticas viajan más rápido que las ondas dinámicas.

La definición del número de Vedernikov, V = v/w, refleja la inequívoca competencia entre las ondas cinemáticas y dinámicas (Ponce, 2023b). A diferencia del número de Froude, que considera sólo ondas dinámicas, el número de Vedernikov compara los dos tipos de ondas y determina que el flujo es estable para V < 1, o inestable para V > 1. En la práctica de la ingeniería hidráulica, la inestabilidad del flujo es una condición necesaria pero no suficiente para la aparición de ondas de rollo (Ponce y Choque Guzmán, 2019) (Fig. 1).

Cornish (1907)

Fig. 1  Fotografía histórica de un tren de ondas de rollo
en los Alpes suizos.

3.  Perspectiva histórica

El desarrollo original del concepto se remonta al trabajo de Vedernikov, traducido de su versión en el idioma ruso (Vedernikov, 1945; 1946). Casi al mismo tiempo, Craya (1945) publicó un artículo con contenido similar en la revista francesa La Houille Blanche. Sin embargo, cabe indicar que el artículo de Craya sobre el tema de la inestabilidad del flujo se publicó en Inglés sólo siete años después (Craya, 1952).

El "número de Vedernikov" como tal se originó con Powell (1948), quien afirmó: "Este criterio, al que yo llamo número de Vedernikov..." El trabajo de Vedernikov, que lamentablemente no era muy claro en su forma original, fue elucidado por Craya (1952), quien afirmó inequívocamente que la inestabilidad del flujo se produce cuando la celeridad de Seddon (onda cinemática) excede la celeridad de Lagrange (onda dinámica).

Chow (1959), en su Capítulo 8, Sección 8, intentó incluir el concepto de número de Vedernikov en su libro de texto. Describió el concepto en términos de las propiedades de fricción y de sección transversal del canal, haciendo eco esencialmente el trabajo de Vedernikov.

Casi tres décadas después, el tema fue aclarado por Ponce (1991a), quien simplificó el trabajo original de Vedernikov expresando el número de Vedernikov, así como el número de Froude, únicamente en términos de la velocidad media del flujo u y las celeridades relativas de onda v y w. De hecho: F = u/w y V = v/w. La relación restante, V/F = v/u se identifica como (β - 1), en la cual β es el exponente de la curva de gasto caudal-area Q = α A β (Cuadro A).

Cuadro A.  Relación entre β y los números de Froude y Vedernikov.

  1. Curva de gasto caudal-area :  Q = α A β .

  2. Celeridad de Seddon:  dQ/dA  (Seddon, 1900).

  3. Celeridad de Seddon (celeridad de la onda cinemática): 
    dQ/dA = α β A β -1 = β (Q /A) = β u .

  4. Celeridad relativa de la onda cinemática:  v = β u - u = (β - 1) u .

  5. Relación V/F = (v /w) / (u /w) = v /u = β - 1 .

  6. El parámetro β completa el trio de parámetros adimensionales, encapsulando ambos números de Froude y Vedernikov.

Ponce y Simons (1977) han confirmado que F = 2 describe el caso de estabilidad neutra para la friccion de Chezy en canales hidráulicamente anchos. Por lo tanto, F = 2 es equivalente a V = 1. Tomados juntos, los números de Froude y Vedernikov describen todo el comportamiento del flujo no permanente en canales. Su relación (β - 1), debido a su sencillez, convierte a β tal vez en el más importante parámetro del flujo en canales.

4.  Efecto de fricción de fondo y sección transveral

Dado que V/F = (β - 1), se puede definir un número de Froude neutralmente estable como sigue: Fns = 1 / (β - 1). Por ejemplo, para la fricción de Chezy en un canal hidráulicamente ancho, para el cual β = 1.5, se concluye que Fns = 2, confirmando las conclusiones de Ponce y Simons (1977). Se observa que desde que Fns es una función sólo de β, esta última reúne a ambos números de Froude y Vedernikov en un solo parámetro, el único capaz de caracterizar completamente la inestabilidad hidrodinámica del flujo en canales.

La Tabla 1 muestra los valores de β y Fns para diversas combinaciones de fricción de fondo y sección transversal (Ponce, 2014). Se observa que el valor de β varía en el rango 3 ≥ β ≥ 1, con un valor alto de β = 3 correspondiente al flujo laminar, y un valor bajo de β = 1 para el canal inherentemente estable (Ponce y Porras, 1995). Por lo tanto, el valor de Fns varía en el rango 0.5 ≤ Fns ≤ ∞, con un valor bajo de Fns = 0.5 para el flujo laminar, y un valor alto de Fns = ∞ para el canal inherentemente estable. La Tabla 1 completa la caracterización de la inestabilidad hidrodinámica para diversos tipos de fricción de fondo y forma de la sección transversal.

TABLA 1.  Valores del número de Froude neutralmente estable Fns para diversos valores de β.
β β - 1 Tipo de fricción de fondo Forma de la sección transversal Fns
3 2 Laminar Hidráulicamente ancha 1/2
8/3 5/3 Mixta laminar-turbulenta
(25% Manning turbulenta)		 Hidráulicamente ancha 3/5
21/8 13/8 Mixta laminar-turbulenta
(25% Chezy turbulenta)		 Hidráulicamente ancha 8/13
7/3 4/3 Mixta laminar-turbulenta
(50% Manning turbulenta)		 Hidráulicamente ancha 3/4
9/4 5/4 Mixta laminar-turbulenta
(50% Chezy turbulenta)		 Hidráulicamente ancha 4/5
2 1 Mixta laminar-turbulenta
(75% Manning turbulenta)		 Hidráulicamente ancha 1
15/8 7/8 Mixta laminar-turbulenta
(75% Chezy turbulenta)		 Hidráulicamente ancha 8/7
5/3 2/3 Manning turbulenta Hidráulicamente ancha 3/2
3/2 1/2 Chezy turbulenta Hidráulicamente ancha 2
4/3 1/3 Manning turbulenta Triangular 3
5/4 1/4 Chezy turbulenta Triangular 4
1 0 Cualquiera Inherentemente estable ∞
.

5.  Número de Vedernikov y difusividad hidráulica

El tránsito de inundaciones en canales implica el cálculo de dos procesos físicos: convección y difusión. La convección es un proceso de primer orden; la difusión es de segundo orden. La convección se caracteriza por la velocidad convectiva o celeridad; la difusión se caracteriza por la difusividad hidráulica. A partir del trabajo fundamental de Hayami (1951), la fórmula de difusividad hidráulica ha experimentado un cambio gradual, a medida que el tema ha madurado con el tiempo. La última expresión de la difusividad hidráulica, en términos del número de Vedernikov, se debe a Ponce (1991a). El Cuadro B describe el desarrollo histórico del concepto de difusividad hidráulica.

Cuadro B.  Desarrollo histórico del concepto de difusividad hidráulica (Nuccitelli y Ponce, 2014).

  1. El concepto fue originado por Hayami (1951), quien expresó la diffusividad hidráulica como sigue:  νh = (uo do)/(2So) = qo / (2So), en la cual uo = velocidad del flujo de equilibrio, do = profundidad del flujo de equilibrio, qo = caudal unitario de equilibrio, y So = pendiente de fondo del canal. La difusividad de Hayami es propiamente una difusividad hidráulica cinemática, porque no incluye la inercia. La relación de Hayami, aplicable a cualquier canal, es:
     νh = qo / (2So) 

  2. Dooge (1973) mejoró el concepto al incluir la inercia en la formulación, definiendo así una difusividad hidráulica dinámica. Su relación, aplicable sólo a un canal hidráulicamente ancho con fricción de Chezy es:
     νh = [qo / (2So)]  [1 - (Fo2/4) ] 

  3. Dooge y otros (1982) formularon la componente inercial de la difusividad como una función de β, el exponente de la curva de gasto. Su relación, aplicable a cual tipo de fricción de fondo y sección transversal es la siguiente:
     νh = [qo / (2So)]  [1 - (β - 1)2 Fo2 ] 

  4. Ponce (1991a, 1991b) mejoró la formulación de difusividad hidráulica expresando la componente inercial en función solamente del número de Vedernikov. La relación, aplicable a un canal de cual tipo de fricción de fondo y sección transversal es la siguiente:
     νh = [qo / (2So)]  [1 - Vo2 ] 

La cuestión de cuán importante es el número de Vedernikov en el cálculo de la difusividad hidráulica merece un tratamiento más exhaustivo. Hayami (1951) desarrolló un valor aproximado para la difusividad hidráulica, excluyendo la inercia. En el caso de que la inercia sea importante, la ecuación de Dooge de 1973 la tiene en cuenta, pero está limitada a la fricción de Chezy en un canal hidráulicamente ancho. Dooge y otros (1982) relajaron este último requisito para canales de cualquier tipo de fricción (laminar, Manning o Chezy) y forma de la sección transversal. Ponce (1991) expresó el componente inercial de la difusividad hidráulica únicamente en términos del número de Vedernikov.

La formulación de Ponce's (1991a) es útil cuando la onda siendo considerada es realmente una onda mixta cinemático-dinámica, situación que parece ser muy poco común en la práctica (Ponce, 2023b). Sin embargo, su atractivo teórico, sin complicar excesivamente los cálculos, continúa siendo una clara ventaja. Aquí se recomienda la formulación de Ponce (1991a) para uso general en aplicaciones de tránsito de avenidas.

6.  Diseño de canales estables

El concepto de número de Vedernikov es muy útil en el diseño de canales para asegurar la estabilidad hidrodinámica. El diseño hidráulico del flujo en canales revestidos empinados requiere una evaluación del número de Vedernikov asociado con el caudal de diseño. Si el número de Vedernikov calculado excede la unidad, existe la posibilidad de que se formen ondas de rollo (Fig. 2). En la literatura en Español se ha hecho referencia a estas ondas como ondas "pulsantes", para denotar el hecho de que invariablemente ocurren como un "tren de ondas de masa" que viajan aguas abajo en un canal a altas velocidades, a menudo peligrosas (Lighthill y Whitham, 1955; Ponce y Choque Guzm&an, 2019).

Fig. 2  Ondas de rollo en un canal lateral empinado, Cabana-Mañazo, Puno, Perú.

El objetivo del diseño debe ser el que las ondas de rollo permanezcan dentro de los límites del canal, para el caudal de diseño adoptado o, mejor aún, diseñar la sección transversal para evitar que se produzcan las ondas de rollo. Esto requiere una comprensión inusual de la naturaleza y el comportamiento de las ondas de rollo. Necesariamente, el análisis se basa en la evaluación del exponente de la curva de gasto β (Tabla 1). Para evitar ondas de rollo (Fig. 3), el β de diseño debe ser el valor más bajo posible, acorde con otros criterios, tales como el costo y la huella geométrica del proyecto.

Cortesía de Jorge Molina Carpio

Fig. 3  Ondas de rollo en el río canalizado Huayñajahuira, La Paz, Bolivia (2016).

El rango factible de variación de β es de 1,0 a 1,67 cuando se utiliza la fricción de Manning y de 1,0 a 1,5 para la fricción de Chezy. Para una sección transversal triangular, β = 1,33 para la fricción de Manning y 1,25 para la fricción de Chezy. No es probable que valores de β cercanos a 1,0, pero superiores (por ejemplo, β = 1,04), desarrollen ondas de rollo. La razón es que β condiciona que la celeridad de la onda cinemática sea mayor que la velocidad media del flujo: ck = βu > u. Para valores de β muy superiores a 1, por ejemplo, β = 1,6, se prevé la posibilidad de que se produzcan ondas de rollo. Cabe observar que el parámetro β es el único parámetro del flujo en canales capaz de predecir el inicio de un evento de onda de rollo de manera precisa y efectiva.

7.  Cálculo en línea

Aquí describimos un cálculo de β utilizando el programa CANALENLINEA15B (https://ton.sdsu.edu/canalenlinea15b.php), una herramienta específicamente diseñada para calcular el valor de β para un canal prismático de sección rectangular, triangular, o trapezoidal. Se presentan dos ejemplos explicados en el Cuadro C. El objetivo es mostrar la variación del número de Vedernikov V con β, confirmando una vez más la relación directa entre éstos.

Cuadro C.  Cálculo del exponente β y del número de Vedernikov V.

  1. Ejemplo 1: Alto valor de β, sección rectangular.

    Caudal = 100 m3/s; ancho de fondo b = 6 m; profundidad de flujo y = 1.638 m; pendiente lateral z = 0; n de Manning = 0.025; pendiente de fondo S = 0.06.

    Nótese que estos datos se asemejan a las condiciones de flujo del canalizado río Huaynajahuira en La Paz, Bolivia (Fig. 4).

    Los resultados de CANALENLINEA15B se muestran en la Fig. 5.

  2. Ejemplo 2: Bajo valor de β, sección trapezoidal.

    Caudal = 100 m3/s; ancho de fondo b = 1 m; profundidad de flujo y = 3.503 m; pendiente lateral z = 0.5; n de Manning = 0.025; pendiente de fondo S = 0.06.

    Esta condición hipotética modifica el Ejemplo 1 reduciendo el ancho de fondo y aumentando la pendiente lateral.

    Los resultados de CANALENLINEA15B se muestran en la Fig. 6.

Fig. 4  El río canalizado Huayñajahuira, en La Paz, Bolivia.

Fig. 5   Resultados de CANALENLINEA15B:  Ejemplo 1.

Fig. 6   Resultados de CANALENLINEA15B:  Ejemplo 2.

En el Ejemplo 1, un canal rectangular, los resultados son: β = 1.58, y V = 1.48, indicando un flujo inestable. Cabe mencionar que el río canalizado Huayñajahuira sufre de eventos recurrentes de ondas de rollo, una situación que ha sido extensamente documentada por Ponce y Choque Guzmán (2019).

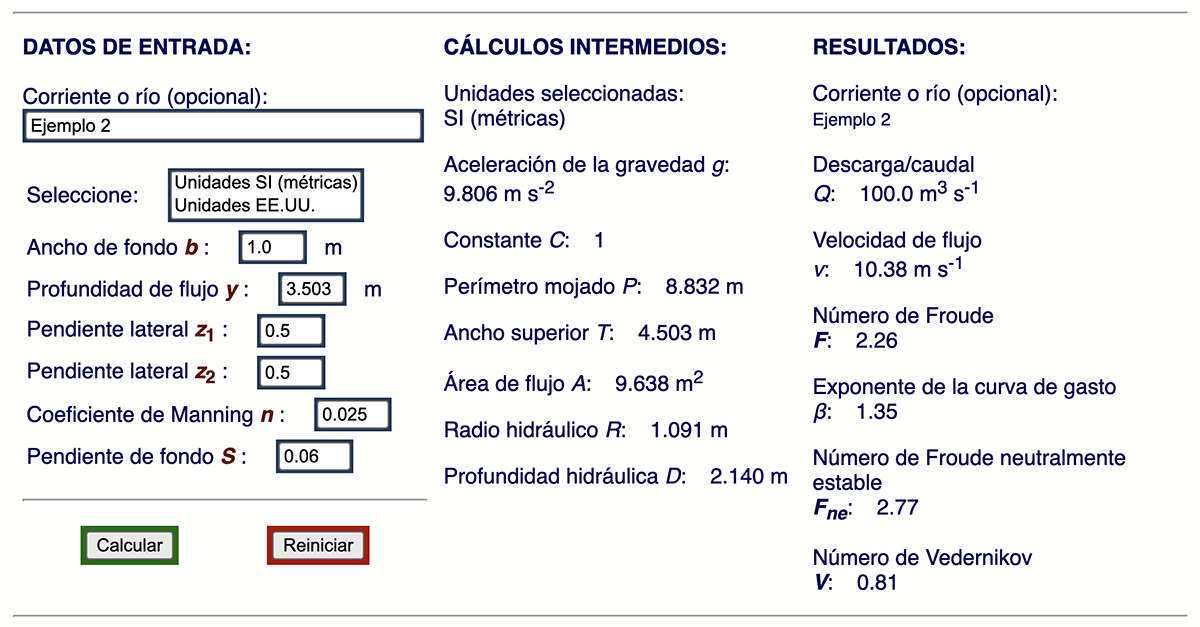
En el Ejemplo 2, un canal trapezoidal, los resultados son: β = 1.35, y V = 0.81, indicando un flujo estable (Ponce, 2021). Se observa la relación directa entre β y V; cuanto menor sea el exponente β, menor será el número de Vedernikov V.

8.  Epílogo

Se revisa, explica y aclara el concepto del número de Vedernikov de la hidráulica de canales. Junto con el número de Froude, constituyen una dualidad inseparable, más ahora que su relación con β, el exponente de la curva de gasto (V/F = β - 1), ha sido claramente establecida y su utilidad en el diseño de canales ampliamente documentada. El uso de una calculadora en línea para β y V en términos de variables hidráulicas reconocidas aumenta la utilidad de la teoría, haciendo posible el evitar las ondas de rollo desde la etapa de diseño. Se presentan dos ejemplos de cálculo con la calculadora en linea CANALENLINEA15B, utilizando datos reales del río Huayñajahuira, en La Paz, Bolivia.

Referencias

Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, Inc, New York, NY.

Lagrange, J. L. de. 1788. Mécanique analytique, Paris, part 2, section II, article 2, 192.

Cornish, V. 1907. Progressive waves in rivers. Journal of the Royal Geographical Society, Vol. 29, No. 1, January, 23-31.

Craya, A. 1945. Calcul graphique des régimes variables dans lex canaux. La Hoiulle Blanche, No. 1, 39-60.

Craya, A. 1952. The criterion for the possibility of roll wave formation. Gravity Waves, National Bureau of Standards Circular No. 521, National Bureau of Standards, Washington, D.C. 141-151.

Dooge, J. C. I. 1973. Chapter 9, Mathematical simulation of surface flow, Linear Theory of Hydrologic Systems, Technical Bulletin No. 1468, Agricultural Research Service, U.S. Department of Agriculture, Washington, DC, October. Extract.

Dooge, J. C. I., W. B. Strupczewski, and J. J. Napiorkowski. 1982. Hydrodynamic derivation of storage parameters of the Muskingum model, Journal of Hydrology, Vol. 54, 371-387.

Hayami, I. 1951.On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, December.

Lighthill, M. J. y G. B. Whitham. 1955. On kinematic waves. I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.

Nuccitelli, N. y V. M. Ponce. 2014. The dynamic hydraulic diffusivity reexamined. Online article. En Español: https://ton.sdsu.edu/difusividad_hidraulica_dinamica_reexaminada.html

Ponce, V. M. y D. B. Simons. 1977. Shallow wave propagation in open channel flow. Journal of Hydraulic Engineering ASCE, 103(12), 1461-1476. En Español: https://ton.sdsu.edu/propagacion_de_ondas_poco_profundas_en_canales_abiertos.html

Ponce, V. M. 1979. On the classification of open channel flow regimes. Proceedings, Fourth National Hydrotechnical Conference, Vancouver, British Columbia, Canada.

Ponce, V. M. 1991a. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779. En Español: https://ton.sdsu.edu/nueva_perspectiva_del_numero_de_vedernikov.html

Ponce, V. M. 1991b. The kinematic wave controversy. Journal of Hydraulic Engineering ASCE, 117(4), 511-525. En Español: https://ton.sdsu.edu/la_controversia_de_la_onda_cinematica.html

Ponce, V. M. y P. J. Porras. 1995. Effect of cross-sectional shape on free-surface instability. Journal of Hydraulic Engineering ASCE, 121(4), 376-380. En Español: https://ton.sdsu.edu/efecto_de_la_forma_de_la_seccion_transversal.html

Ponce, V. M. 2014. Fundamentos de Hidráulica de Canales. Texto en línea. https://ton.sdsu.edu/canales/index.html

Ponce, V. M. y B. Choque Guzmán. 2019. The control of roll waves in channelized rivers. Artículo en línea.
https://ton.sdsu.edu/the_control_of_roll_waves.html

Ponce, V. M. 2021. Design of a stable channel on a steep slope using the exponent of the rating. Artículo en línea. https://ton.sdsu.edu/design_of_a_stable_channel_using_the_exponent_of_the_rating.html

Ponce, V. M. 2023a. Los estados de flujo. Artículo en línea. https://ton.sdsu.edu/estados_de_flujo.html

Ponce, V. M. 2023b. Kinematic and dynamic waves: The definitive statement. Artículo en línea.
https://ton.sdsu.edu/kinematic_and_dynamic_waves.html

Powell, R. W. 1948. Vedernikov's criterion for ultra-rapid flow. Transactions, American Geophysical Union, Vol. 29, No. 6, 882-886.

Seddon, J. A. 1900. River hydraulics. Transactions, ASCE, Vol. XLIII, 179-243, June.

Vedernikov, V. V. 1945. Conditions at the front of a translation wave disturbing a steady motion of a real fluid. Doklady Akademii Nauk USSR, 48(4), 239-242.

Vedernikov, V. V. 1946. Characteristic features of a liquid flow in an open channel. Doklady Akademmi Nauk USSR, 52(3), 207-210.

240516