[Canais Não Erodíveis]   [Canais Erodíveis]   [Tração]   [Tração Admissível]   [Outras Características]   [Questões]   [Problemas]   [Referências]   •   CAPÍTULO 6:  PROJETO DE CANAIS 6.1  CANAIS NÃO ERODÍVEIS [Canais Erodíveis]   [Tração]   [Tração Admissível]   [Outras Características]   [Questões]   [Problemas]   [Referências]   •   [Topo]   Existem dois tipos de canais: (1) não erodível e (2) erodível. Canais não erosíveis normalmente são revestidos com um material de construção rígido, como alvenaria de concreto ou pedra. Os canais erosíveis são escavados na superfície do solo e, portanto, diretamente em contato com o solo subjacente. O design de canais erosíveis é muito mais complexo que o dos canais não erosíveis. O projeto de canais não erosíveis começa com a escolha de uma fórmula de fluxo uniforme (Capítulo 5). Os seguintes fatores são considerados no projeto de canais não erosíveis: Rigidez da superfície A rugosidade da superfície (atrito limite) é determinada pelo tipo e acabamento do material que reveste o limite do canal. Geralmente, superfícies mais grossas têm maior atrito do que superfícies mais suaves (Fig. 6-1). Fig. 6-1  Canal revestido com alvenaria. Velocidade mínima admissível Todos os canais transportam uma certa quantidade de sedimentos (areia, silte, argila). Portanto, o fluxo em canais de declive muito suave pode levar à deposição excessiva de sedimentos. Assim, é necessária uma velocidade mínima admissível, isto é, uma inclinação mínima do fundo, para evitar o assoreamento das calhas fluviais. Declividade inferior máxima Todos os canais não erosíveis tendem a desenvolver ondas de rolagem se o número de Vedernikov for superior a 1 (V > 1, como mostra o Capítulo 1). Para evitar as ondas de rolagem, a inclinação inferior deve ser mantida abaixo de um valor máximo, que é função da hidráulica do fluxo. Como exemplo, a Fig. 6-2 mostra uma série de quedas implementadas em um canal para reduzir a declividade inferior. Fig. 6-2  Quedas ao longo do canal para minimizar a declividade do canal La Joya em Arequipa, Peru. 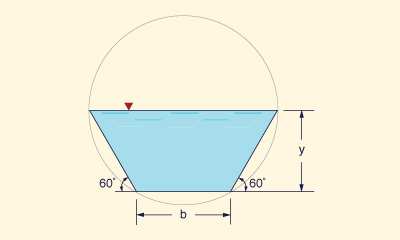A seção do canal de máxima condução e, portanto, vazão máxima, é aquela que possui o perímetro molhado mínimo para uma determinada área de escoamento. Esse formato da seção transversal é conhecido como a melhor seção hidráulica. A melhor seção circular hidráulica é um semicírculo. A melhor seção trapezoidal hidráulica é um hexágono semi-regular inscrito em um círculo (Chow, 1959) (Fig. 6-3). Na prática, no entanto, outras considerações de projeto são geralmente mais importantes do que a da máxima condução. Fig. 6-3  Seção hidráulica ideal de forma trapezoidal. Talude A inclinação lateral é z H : 1 V, em que z = 0 para uma seção retangular e z > 0 para uma seção trapezoidal, é uma decisão de projeto que varia de acordo com as condições locais (Fig. 6-4). As inclinações laterais típicas variam de z = 0 para z = 3. Fig. 6-4  Transição do canal da forma retangular para a trapezoidal. Borda livre A borda livre é a profundidade vertical medida acima da profundidade do canal de projeto, até a profundidade total do canal (Fig. 6-5). Destina-se a levar em consideração um fator de segurança e minimizar o excesso de ondas. Fig. 6-5  Borda livre do canal de San Luis, California, EUA. Redução do risco de escorregamentos Nos revestimentos de encostas, deve-se tomar cuidado para reduzir o risco de escorregamentos locais, que, dependendo da sua extensão, podem tornar o canal inoperante. Algumas encostas são propensas a escorregamentos, enquanto outras não. É necessária uma investigação completa do local geológico / geotécnico para reduzir o risco de escorregamentos. A Figura 6-6 mostra uma violação gerada por escorregamentos no Canal La Cano, Arequipa, Peru, que ocorreu em 4 de novembro de 2010 (veja o vídeo relacionado). Fig. 6-6  Deslizamento gerado no canal La Cano, em Arequipa, Peru, que ocorreu em 04 de novembro de 2010. Revestimento do canal Os canais podem ser revestidos com diversos materiais, entre eles o concreto, alvenaria, pedra, aço, ferro fundido, madeira, vidro e plástico. O revestimento do canal reduz o atrito dos limites e minimiza os custos de manutenção do canal. A Figura 6-7 mostra o rio Santa Ana, na praia de Huntington, Califórnia, EUA, pavimentado com concreto para reduzir o estágio de inundação e controlar as mesmas. Fig. 6-7  Canal natural pavimentado de Santa Ana, na praia de Huntington,California, EUA. A Figura 6-8 mostra o córrego de Alamar, em Tijuana, México, revestido com concreto em 2013. Observe que as práticas atuais de projeto ambiental desencorajam fortemente o revestimento de canais naturais com concreto. Fig. 6-8  Córrego Alamar em Tijuana, Baja California, México. Velocidade mínima admissível Toda a água transporta uma certa quantidade de sólidos em suspensão, na forma de sedimentos que foram arrastados de algum lugar à montante e estão sendo transportados pelo fluxo. Os valores típicos da carga suspensa são de 200 a 300 partes por milhão (ou ppm, equivalente, nessa faixa, a mg/L) (Ponce, 1989). A condição de não escorregamento no limite do canal (ou seja, a velocidade longitudinal local é zero no limite do canal) produz tensões de cisalhamento e resulta no transporte de sedimentos. Uma vez arrastado, esse sedimento precisa ser transportado através do canal; caso contrário, ele se deposita no fundo do canal, eventualmente obstruindo o mesmo. A velocidade mínima para evitar a sedimentação/entupimento da calha é a velocidade mínima admissível. 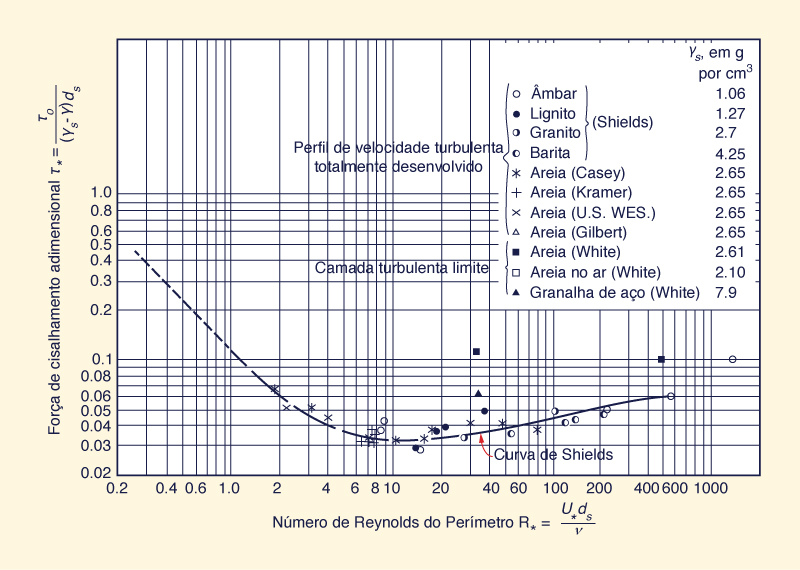A avaliação da velocidade mínima admissível pode ser realizada pelo critério Shields para o início do movimento. Este critério está incorporado no diagrama de Shields, mostrado na Fig. 6-9, que relaciona a tensão de cisalhamento adimensional τ* com o limite número de Reynolds R*. A curva sólida na Fig. 6-9 não separa nenhum movimento abaixo da curva do movimento acima da curva. Fig. 6-9  Diagrama de Shields para a iniciação do movimento (American Society of Civil Engineers, 1975). Número mínimo de Froude e velocidade mínima admissível A lei do atrito quadrático, Eq. 5-3, é reformulada aqui com τo como a tensão de cisalhamento inferior:   τo  =  ρ f V 2   (6-1) O critério de Shields para o início do movimento é:                  τo τ* = _____________  ≥  τ*c           (γs - γ ) ds (6-2) Em que:   τ* = tensão de cisalhamento adimensional;                 γs = peso específico de partículas de sedimentos;                 γ  = peso específico de água;                 ds = diâmetro das partículas de sedimentos;                 τ*c = tensão de cisalhamento adimensional crítica. A Figura 6-9 mostra a curva de Shields, ou seja, a variação da tensão de cisalhamento adimensional crítica τ*c com o limite número de Reynolds R*:             U* ds R* =  _________                ν (6-3) Em que:   U* = velocidade de cisalhamento (τo /ρ)1/2 = ( f )1/2 V  ;                 ν  = viscosidade cinemática. O número de Froude F é:               V F = ___________          (g D )1/2 (6-4) Em que:   V = velocidade média;                 D = profundidade hidráulica;                 g = aceleração da gravidade. Substituindo as Eqs. 6-1 e 6-4 na Eq. 6-2:              f D F 2 _____________________  ≥  τ*c     [ (γs / γ ) - 1 ] ds (6-5) Na maioria dos casos de interesse prático, a proporção de pesos específicos de sedimentos e água γs /γ é igual a 2,65. Portanto, em termos de número de Froude, o critério de Shields para o início do movimento reduz-se a:              1,65 τ*c (ds / D ) F  ≥  [ __________________ ] 1/2                          f (6-6) Para aplicações práticas, um valor constante de tensão de cisalhamento adimensional crítica τ*c = 0,04 pode ser considerado. Na Fig. 6-9, é visto que esse valor abrange a faixa:  4 ≤ R* ≤ 60. Portanto:              0,066 (ds / D ) F  ≥  [ ________________ ] 1/2                        f (6-7) A Equação 6-7 é o critério prático de Froude baseado em Shields para o início do movimento, aplicável por meio de uma ampla gama de números limites de Reynolds. Como exemplo prático do uso da Eq. 6-7, assuma ds = 0,4 mm, D = 1 m, e um fator de atrito adimensional de Chezy médio de f = 0,0035 (equivalente a um fator de atrito de Darcy-Weisbach f = 0,028). A aplicação da Eq. 6-7 leva a:               F  ≥  0,087                         (6-8) Combinando Eqs. 6-4 e 6-7:              0,066 (g ds) V  ≥  [ ______________ ] 1/2                       f (6-9) Da Eq. 6-9, a velocidade mínima admissível para esta condição de fluxo é: Vmin = 0,27 m/s. Um valor um pouco mais preciso do número mínimo de Froude e da velocidade mínima admissível pode ser obtido usando o valor real da tensão de cisalhamento crítica adimensional na Eq. 6-7, ao invés da aproximação conveniente τ*c = 0,04. Este procedimento, no entanto, requer uma iteração. Para esse fim, é sugerido o seguinte algoritmo: Suponha R* Usando a Fig. 6-9, encontre τ* = τ*c Com τ*, use Eq. 6-2 para resolver τo Usando a Eq. 6-1, calcule a velocidade de cisalhamento U* = (τo /ρ)1/2 Usando a Eq. 6-3, calculate o novo valor de R* Pare se o novo valor de R* for o mesmo que o assumido na Etapa 1 (dentro de uma tolerância pequena) e use o último valor de τ*c (calculado na Etapa 2) na Eq. 6-6; Caso contrário, retorne à Etapa 1, usando o novo valor de R* como o valor assumido e repita a iteração.  Exemplo 6-1 Suponha os seguintes dados de canal: diâmetro das partículas ds = 0,4 mm, profundidade hidráulica D = 1 m, fator de atrito adimensional de Darcy-Weisbach f = 0,0035 e temperatura da água T = 20°C. Usando o critério de Shields para o início do movimento, calcule o número mínimo de Froude e a velocidade mínima admissível.   CÁLCULO ONLINE. Usando a calculadora EMLINHA SHIELDS VELOCIDADE, o número mínimo de Froude é Fmin = 0,081 e a velocidade mínima admissível é Vmin = 0,25 m/s. Observe que esses resultados são um pouco mais conservadores do que os obtidos com as Eqs. 6-7 e 6-9. Declividade do canal A declividade de projeto do canal é geralmente governada pelo revestimento escolhido e pela topografia predominante. A declividade real de projeto depende da finalidade do canal. Por exemplo, os canais usados para irrigação e usinas hidrelétricas requerem pequenas inclinações, para não perderem muita carga durante a condução. As encostas laterais dependem do solo local e das condições de construção, geralmente o mais íngreme possível. Para canais revestidos, uma inclinação lateral de 1,5H:1V é recomendada como padrão pelo Bureau of Reclamation dos EUA, para uso na maioria dos canais. Para canais revestidos e com declividades acentuadas, quando o número de Vedernikov excede 1, surge a possibilidade de desenvolvimento de ondas de rolagem (Capítulo 1 ). Borda livre A borda livre é a distância vertical da parte superior do canal à superfície da água na condição de projeto. Essa distância deve ser suficiente para impedir que ondas ou flutuações na superfície da água transbordem pelos lados do canal. Esse recurso se torna importante, particularmente no projeto de calhas elevadas, pois a subestrutura da calha pode ser ameaçada por um transbordamento (Fig. 6-10). Fig. 6-10  Conduto Dulzura no Condado de San Diego, California, EUA, com transbordamento depois de chuva significativa no dia 05 de março de 2005. Não há uma regra universalmente aceita para a determinação da borda livre. Ondas geradas pelo vento ou ação das marés podem induzir ondas altas, que precisariam ser mantidas dentro dos limites do canal. As bordas livres que variam de menos de 5% a mais de 30% da profundidade do fluxo de projeto são práticas comuns. Para calhas com declividades suaves, internas e semicirculares nas tangentes, transportando água a velocidades não superiores à velocidade crítica, com no máximo 8 pés/s (2,4 m/s), a experiência indicou que uma borda livre com 6% do diâmetro da calha é apropriado. Para calhas em curvas, a borda livre deve ser aumentada para evitar que a água se incline (Chow, 1959). Observe que os critérios de projeto hidráulico geralmente permitem o uso de toda ou de parte da borda livre para acomodar a provável máxima de inundação (Ponce, 1989). De acordo com o Bureau of Reclamation dos EUA, o alcance aproximado da borda livre se estende de 0,3 m (1 pés) a 1,2 m (4 pés) para pequenas laterais com profundidades rasas em canais de até 3.000 cfs ou pés cúbicos por segundo (85 m3/s) ou mais. A seguinte fórmula é aplicável:   Fb  =  ( C y ) 1/2   (6-10) Em que:   Fb = borda livre (em pés);                 y = profundidade da água no canal (em pés);                 C = coeficiente de vazão do canal. O coeficiente varia de C = 1,5 para um canal de capacidade de 20 pés cúbicos por segundo (0,57 m3/s) a C = 2,5 para um canal de capacidade de 3.000 pés cúbicos por segundo (85 m3/s) ou mais. 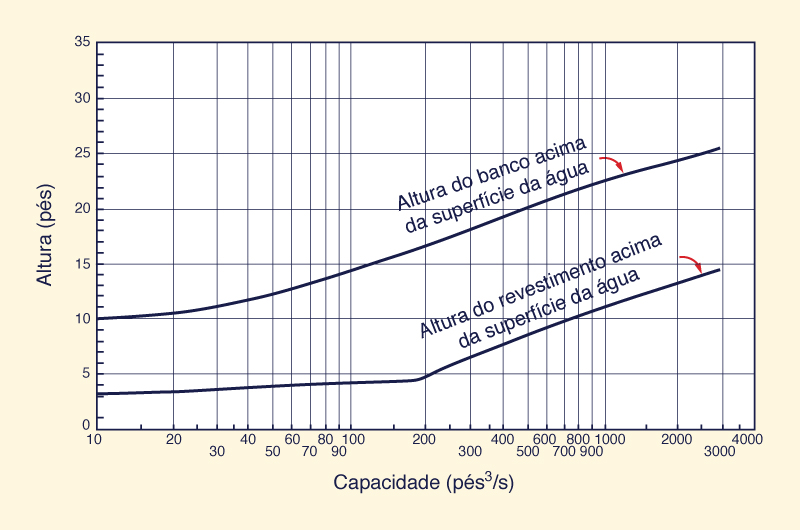A Figura 6-11 mostra a altura do revestimento e a altura das margens recomendadas pelo Bureau of Reclamation dos EUA e, aplicáveis ao projeto da borda livre. Fig. 6-11  Altura do revestimento recomendada pelo Bureau of Reclamation dos EUA e altura do revestimento das paredes laterais ou bancos (Chow, 1959). 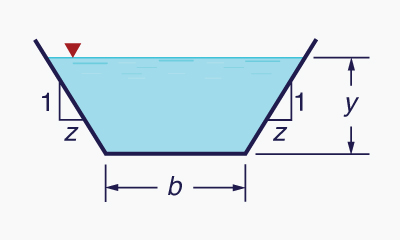Dimensões da seção As etapas a seguir são realizadas para escolher as dimensões de uma seção transversal de um canal: Selecione a vazão de projeto Q ; Selecione a largura inferior b ; Selecione a inclinação lateral z  [z H:1V] (Fig. 6-12); Fig. 6-12  Desenho esquemático da definição da largura de fundo b e inclinação lateral z. Selecione a inclinação inferior S ; Estime o valor de n de Manning (Capítulo 5:  Coeficiente de rugosidade de Manning); Usando Q, b, z, S, and n (Etapas 1 a 5), cacule a profundidade normal yn, velocidade normal vn, e normal número de Froude Fn (Capítulo 5:  Determinação do escoamento uniforme); Verifique se a velocidade normal vn e o número de Froude normal Fn são suficientemente grandes para evitar o entupimento da calha com sedimentos (veja os conceito sobre a velocidade mínima admissível descrita neste capítulo); Selecione a borda livre apropriada Fb . 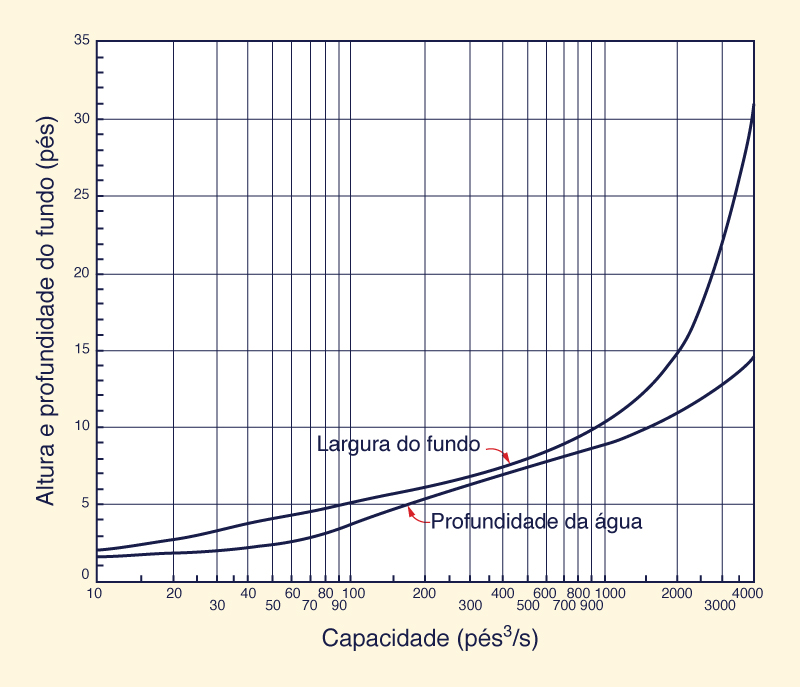A Figura 6-13 mostra a largura do fundo e a profundidade da água recomendadas pelo Bureau of Reclamation dos EUA. Fig. 6-13  Largura do fundo e profundidade da água em canais revestidos de acordo com a recomendação do Bureau of Reclamation dos EUA (Chow, 1959).   Exemplo 6-2. Projete um canal para as seguintes condições de fluxo: Q = 10 m3/s; b = 5 m; z = 2; S = 0,0016; n = 0,025. Usando a Eq. 5-55, por iteração, a profundidade normal é yn = 1,049 m e a velocidade normal é vn = 1,342 m/s. O número de Froude com base na profundidade normal é Fn = 0,418. O número de Froude calculado mostra-se muito maior que 0,087 (Eq. 6-8), o valor mínimo necessário para evitar a deposição de sedimentos. Assume-se que a borda livre é de Fb = 0,6 m.   CÁLCULO ONLINE. Usando a calculadora CANAL EMLINHA 01, a profundidade normal é yn = 1,049 m; a velocidade normal é vn = 1,342 m/s; o número de Froude (com base na profundidade hidráulica D = 0,81 m) é: Fn = 0,476. Observe que o número verdadeiro de Froude é aquele baseado na profundidade hidráulica (Eq. 4-6). Para um canal hidraulicamente amplo, para o qual D ≅ R, ambos os números de Froude são aproximadamente os mesmos. A Figura 6-14 mostra um grande canal construído em 1993 no Ceará, Brasil, com o objetivo de mitigar uma seca regional. As características hidráulicas são: Q = 8,32 m3/s, b = 5 m, z = 1,5, S = 0,00005, e n = 0,015. Usando a calculadora CANAL EMLINHA 01, a profundidade normal é yn = 1,915 m, a velocidade normal é vn = 0,552 m/s e o número de Froude é Fn = 0,149. Cogerh Fig. 6-14  Canal do Trabalhador, no Ceará, Brasil em 1993. 6.2  CANAIS ERODÍVEIS [Tração]   [Tração Admissível]   [Outras Características]   [Questões]   [Problemas]   [Referências]   •   [Topo]   [Canais Não Erodíveis]   O projeto de um canal erodível é muito mais complexo do que o de um canal não erodível. A estabilidade a longo prazo do limite do canal depende das propriedades do material que reveste o limite (areia, silte, argila e combinações dos mesmos) e das propriedades do sedimento sendo transportado pelo fluxo. Mudanças na descarga de água e sedimentos resultam em mudanças na seção transversal, profundidade do canal, largura do canal ou ambos. A estabilidade do limite do canal é normalmente avaliada em termos de dois critérios: Velocidade máxima admissível; Tração máxima admissível. Dada a Eq. 6-1, esses dois métodos estão relacionados da seguinte maneira:   τo max  =  ρ f (Vmax )2   (6-11)  Exemplo 6-3. Calcule a velocidade máxima admissível correspondente a uma tensão de tração máxima admissível de 20 N/m2. Suponha  f = 0,0035, ou seja, Darcy-Weisbach f = 0,028. Usando a Eq. 6-11: Vmax = [τo max / (ρ f ) ] 1/2 = [ 20 N/m2 / (1000 N s2/m4 × 0,0035 ) ] 1/2 = 2,39 m/s.  Exemplo 6-4. Calcule a velocidade máxima admissível correspondente a uma tensão de tração máxima admissível de 0,1 lb/pés2. Suponha f = 0,005, ou seja, Darcy-Weisbach f = 0,04. Usando a Eq. 6-11: Vmax = [τo max / (ρ f ) ] 1/2 = [ 0,1 lb/pés2 / (1,94 lbs-s2/pés4 × 0,005 ) ] 1/2 = 3,21 pés/s. Canais vegetados A Tabela 6-1 mostra os valores típicos de tração máxima admissível para vários tipos de revestimentos de canais vegetados. Tabela 6-1  Valores típicos de tração máxima admissível. Revestimento de canal Tração máxima admissível (N/m2) (lb/pés2) Gramado (plantado a pouco tempo) 20-30 0,42-0,63 Gramado (plantado a muito tempo) 15-18 0,31-0,38 Fascino (entrelaçado) (em inglês, fascine sausage) 60-70 1,25-1,46 Fascino (em rolo) (em inglês, fascine roll) 100-150 2,09-3,13 Fascino (misturado com rocha ou concreto) (em inglês, weighted fascine) 60-100 1,25-2,09 Colchão escovado (em inglês, brush mattress) 150-300 3,13-6,26 Rochas estaqueadas com arbustos (em inglês, live stake) > 140 > 2,92 Árvores 80-140 1,67-2,92 Gabiões 80-140 1,67-2,92 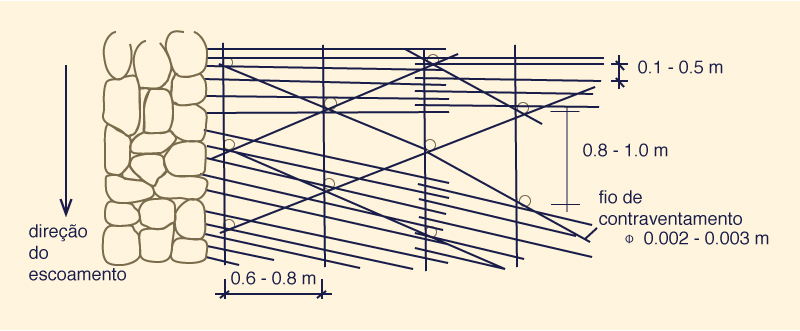O fascino é uma das técnicas empregadas em projetos de bioengenharia. Para sua consulta, veja os sites Fascine e Projetos de Bioengenharia (em inglês). A Figura 6-15 mostra detalhes do projeto de um revestimento de canal usando um colchão escovado. Fig. 6-15 (a)  Projeto de colchão escovado:  vista superior. 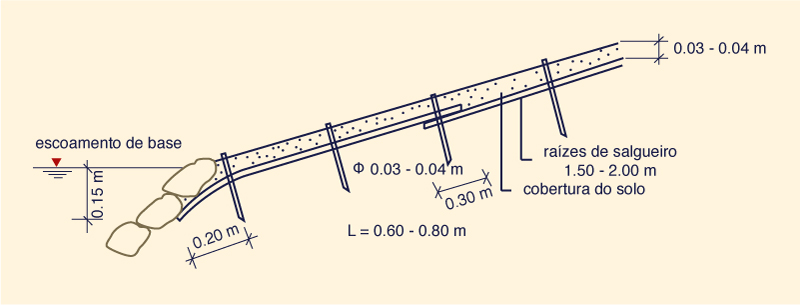Fig. 6-15 (b)   Projeto de colchão escovado:  vista lateral. Fig. 6-15 (c)   Projeto de colchão escovado:  vista lateral após alguns meses de plantio. Fig. 6-15 (d)   Projeto de colchão escovado:  vista após a sua conclusão. 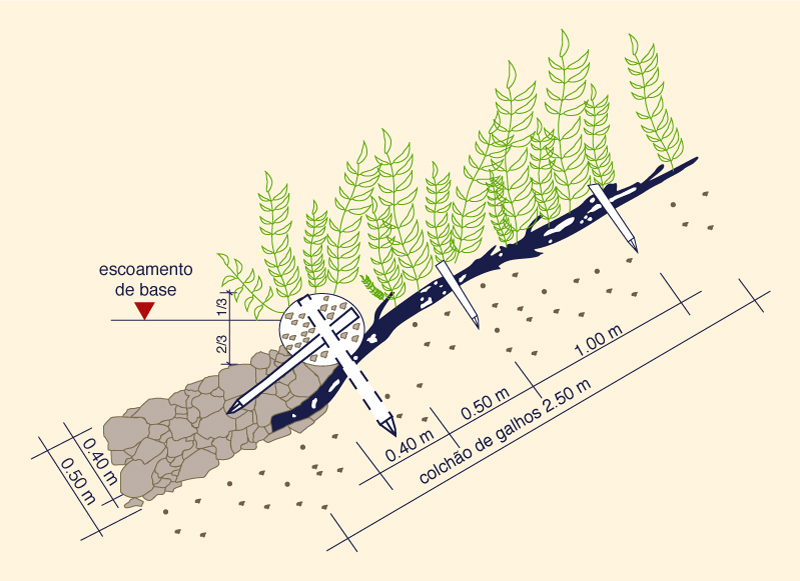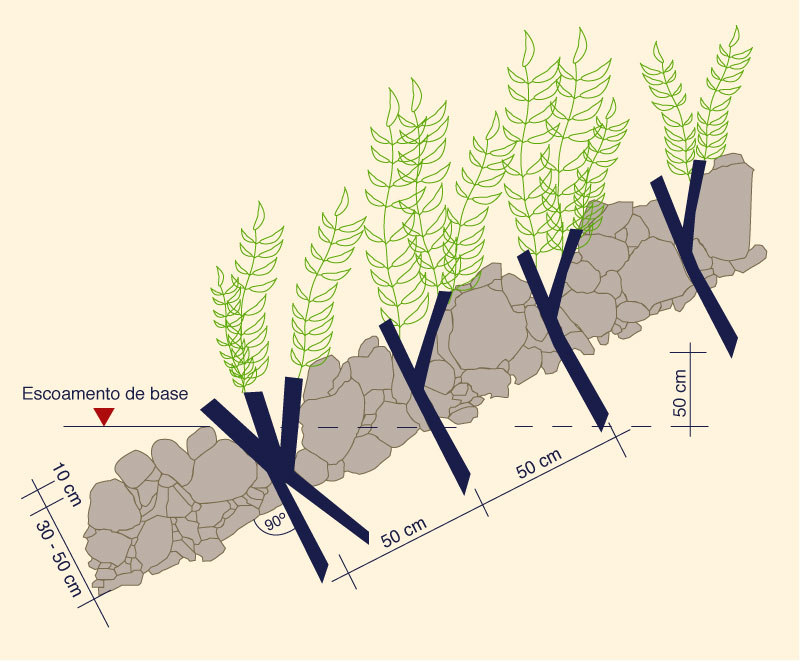A Figura 6-16 mostra detalhes de um revestimento de canal usando rochas estaquadas com arbustos. Fig. 6-16 (a)  Desenho esquemático de rochas estaqueadas com arbustos. Fig. 6-16 (b)  Rochas estaqueadas com arbustos: logo após a sua instalação. Fig. 6-16 (c)  Rochas estaqueadas com arbustos: algum tempo após a sua instalação. Fig. 6-16 (d)  Rochas estaqueadas com arbustos: 2 a 5 anos após a sua instalação. Fig. 6-16 (e)  Rochas estaqueadas com arbustos:  projeto concluído. Canais revestidos de gabião Um sistema de gabião é um agrupamento de pedras revestido por uma malha de arame e ancorado a uma ladeira (Fig. 6-17). Em cada bloco há um conjunto de pedras com tamanhos variados, mas que possuem a mesma resistência ao deslocamento devido à energia da água. Essa é uma vantagem particular do uso de gabiões em áreas de difícil acesso. Os gabiões também podem ser usados em canais com paredes mais íngremes (até verticais), podendo ser construídos com material disponível no mercado ou de vedação de arame. Unknown Fig. 6-17  Implantação da estrutura dos gabiões. 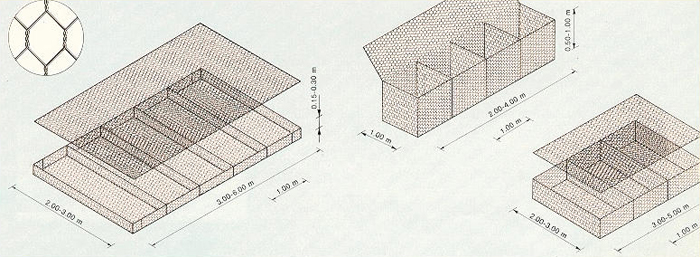Os sistemas de gabiões fornecem uma maneira eficaz de controlar a erosão em córregos, rios e canais. Eles são normalmente projetados para suportar velocidades de canal elevadas [5 m/s (15 pés/s) ou superiores]. Os gabiões são construídos por unidades individuais que variam em comprimento de 2 m (6 pés) a quase 30 m (100 pés); portanto, as aplicações podem variar de valas pequenas a canais grandes (Fig. 6-18). Unknown Fig. 6-18  Dimensões de gabiões em caixas ou valas. Os canais de gabiões são estruturas que unem o bloco aos canais. Quando as rochas do mesmo tamanho são usadas nos gabiões, a velocidade aceitável é de três a quatro vezes a velocidade do bloco. Ao contrário do concreto, os gabiões podem ser vegetados para se misturarem à paisagem natural (Fig. 6-19). Os canais de gabião com vegetação têm as seguintes vantagens: Permitir infiltração e exfiltração; Filtrar contaminantes; Mais flexível do que canais pavimentados Proporcionar maior dissipação de energia que os canais de concreto Melhorar o habitat da flora e fauna Mais esteticamente agradável Menor custo de instalação, embora seja necessária alguma manutenção. Os valores de n de Manning para canais revestidos por gabião estão normalmente na faixa de 0,025 ≤ n ≤ 0,030. Fig. 6-19  Revestimento de canal usando gabiões. 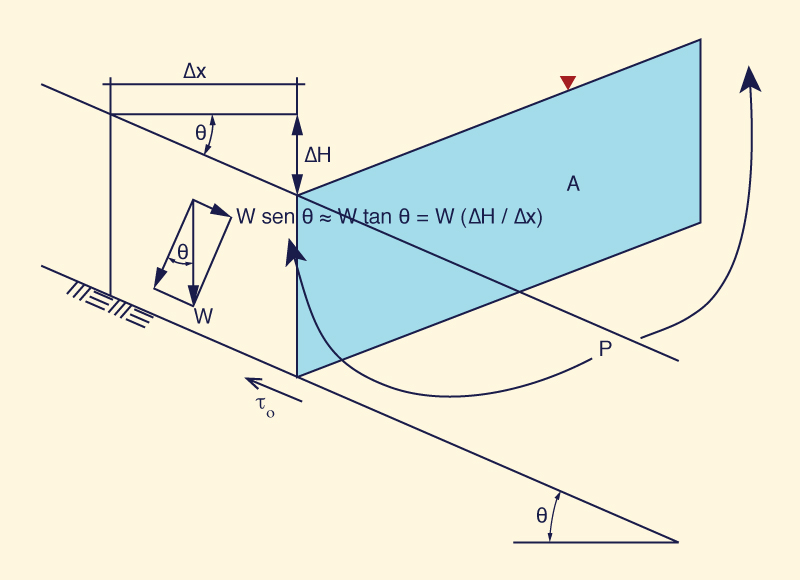6.3  TRAÇÃO [Tração Admissível]   [Outras Características]   [Questões]   [Problemas]   [Referências]   •   [Topo]   [Canais Não Erodíveis]   [Canais Erodíveis]   A força de tração é a soma das tensões de cisalhamento (de tração) sobre uma área do limite do canal. Sob condições de equilíbrio, para desenvolver a equação de tração, a força gravitacional atuante é igual à força de atrito resistente. A força gravitacional é (Fig. 6-20):   W sen θ  ≅  W tan θ  =  W (ΔH /Δx )   (6-12) Em que:   W  = peso do volume de controlo da área A;                Δx  = comprimento do trecho;                ΔH = queda ao longo do volume de controle;                   θ = declividade de fundo do canal. Fig. 6-20  Desenho esquemático da derivação da equação de tração. Uma vez que S = ΔH /Δx, segue que a força gravitacional atuante é:   Fg  =  γ A Δx S   (6-13) A força de atrito resistente é:   Ff  =  τo P Δx   (6-14) Em que:  τo  = tensão de cisalhamento no fundo do canal;                ΔP = perímetro molhado. Igualando as forças gravitacionais e de atrito:   τo  =  γ R S   (6-15) Em que:   R = A /P = raio hidráulico. 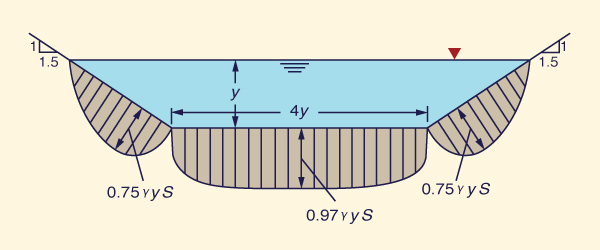Para canais hidraulicamente amplos, nos quais R ≅ D ≅ y,   τo  =  γ y S   (6-16) A tração varia ao longo do perímetro molhado, atingindo um valor de pico no meio do canal. A Figura 6-21 mostra uma variação típica para uma seção transversal trapezoidal, na qual b/y = 4 e z = 1,5. Fig. 6-21  Variação de tração em um canal trapezoidal com b/y = 4 e z = 1,5 (Chow, 1959). 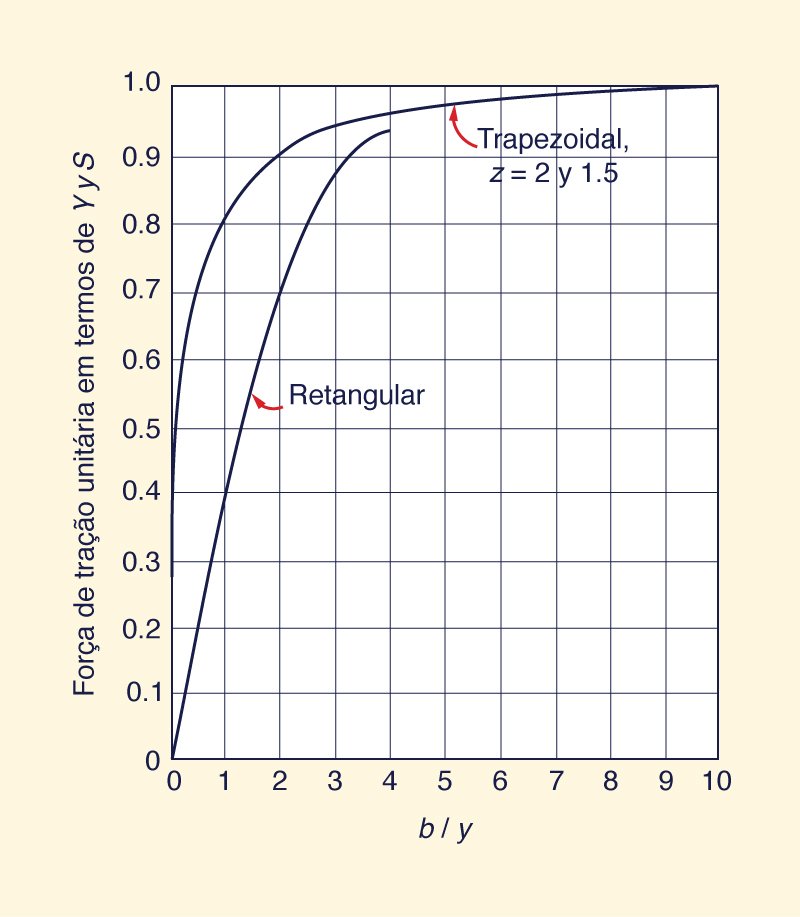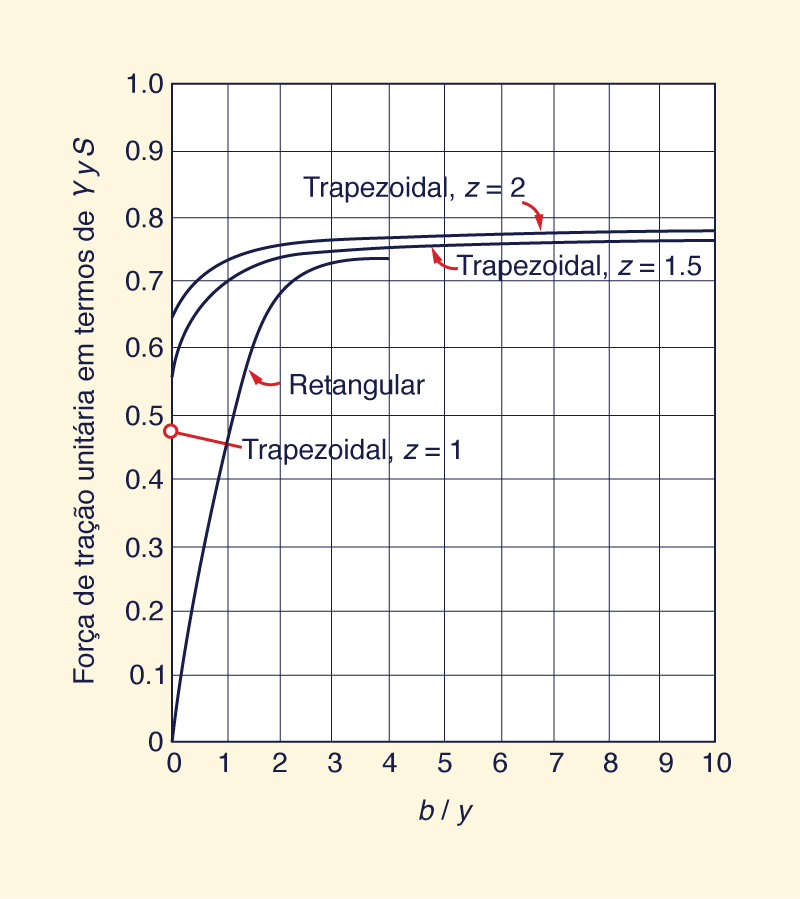No centro do leito do canal, a tração se aproxima assintoticamente do seu valor máximo (máximo): τb = γyS , conforme mostrado na Fig. 6-22. Ao longo dos lados do canal, a tração se aproxima assintoticamente de uma fração do valor total: τs = 0,78 γyS , como mostrado na Fig. 6-23. Fig. 6-22  Variação da tração máxima no fundo do canal com o fator de aspecto b/y (Chow, 1959). Fig. 6-23   Variação da tração máxima nas laterais do canal com o fator de aspecto b/y (Chow, 1959). Relação da força de tração A Figura 6-24 mostra três partículas no limite do canal, uma no lado esquerdo, outra no lado direito e a terceira no nível do leito do canal. A razão de força de tração K é definida como:            a τs            τs K  =  _______  =  ______            a τL            τL (6-17) Em que: a  = área efetiva da partícula;               τs = tensão de cisalhamento;               τL = tensão de cisalhamento em terreno nivelado. 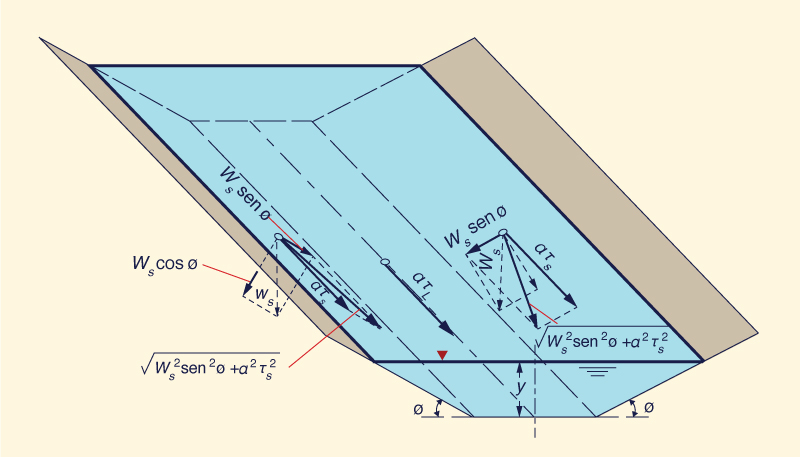Fig. 6-24  Desenho esquemático das forças atuantes em uma partícula sobre o leito (Chow, 1959). A razão K é uma função da inclinação lateral do canal φ e do ângulo de repouso θ do material que forma o leito do canal. Para derivar K , considere as duas forças que estão agindo sobre uma partícula de peso submerso Ws repousando na lateral do canal, com tração τs (Fig. 6-20): A força de tração:  aτs; O componente de força gravitacional ao longo da lateral:  Ws sen φ. A força resultante que atua ao longo do plano lateral é:   Fa  =  (Ws2 sen2φ  +  a2τs2)1/2   (6-18) No equilíbrio, a força resistente é igual à força atuante. Na mecânica dos sólidos, a força resistente é igual à força normal (Ws cosφ ) multiplicada pelo coeficiente de atrito (tanθ ):   Fr  =  Ws  cosφ  tanθ   (6-19) Portanto:   Ws  cosφ  tanθ  =  (Ws2 sin2φ  +  a2τs2)1/2   (6-20) Elevando os dois lados ao quadrado:   Ws2 cos2φ  tan2θ  =  Ws2 sen2φ  +  a2τs2   (6-21)   a2τs2  =  Ws2 cos2φ  tan2θ  -  Ws2 sin2φ   (6-22)   τs2  =  (Ws /a)2 cos2φ  tan2θ  -  (Ws /a)2 sin2φ   (6-23)                                                            tan2φ τs2  =  (Ws /a)2 cos2φ  tan2θ  [ 1  -  _________ ]                                                            tan2θ (6-24)                                                      tan2φ τs  =  (Ws /a) cosφ  tanθ  [ 1  -  _________ ] 1/2                                                      tan2θ (6-25) A equação 6-25 é a tensão de cisalhamento no lado de um canal com ângulo de inclinação lateral φ e ângulo de repouso θ. Para uma superfície no nível, com φ = 0: sen φ = 0 e cos φ = 1. Assim, o equilíbrio de força da Eq. 6-20 reduz para:   Ws  tanθ  =  aτL   (6-26) Portanto, a tensão de cisalhamento que causa movimento iminente em uma superfície nivelada é:   τL  =  (Ws /a) tanθ   (6-27) Combinando as Eqs. 6-17, 6-25 e 6-27, a relação da força de tração é:                                tan2φ K  =  cosφ  [ 1  -  _________ ] 1/2                                tan2θ (6-28) Sabe-se que K é apenas uma função de φ e θ. A equação 6-28 é equivalente a (veja no quadro a seguir):                       sen2φ K  =   [ 1  -  __________ ] 1/2                       sen2θ (6-29) Derivação da Eq. 6-29 A equação 6-28 é simplificada de acordo com as relações trigonométricas pré-estabelecidas:                                tan2φ K  =  cosφ  [ 1  -  _________ ] 1/2                                tan2θ (6-28)                               cos2φ  tan2φ K  =   [ cos2φ  -  ________________ ] 1/2                                    tan2θ (6-28a)                               sen2φ K  =   [ cos2φ  -  _________ ] 1/2                               tan2θ (6-28b)                               sen2φ  cos2θ K  =   [ cos2φ  -  ________________ ] 1/2                                    sen2θ (6-28c)                                   sen2φ  (1 - sen2θ) K  =   [ 1 - sen2φ  -  _____________________ ] 1/2                                            sen2θ (6-28d)                       sen2φ K  =   [ 1  -  __________ ] 1/2                       sen2θ (6-29) Ângulo de repouso 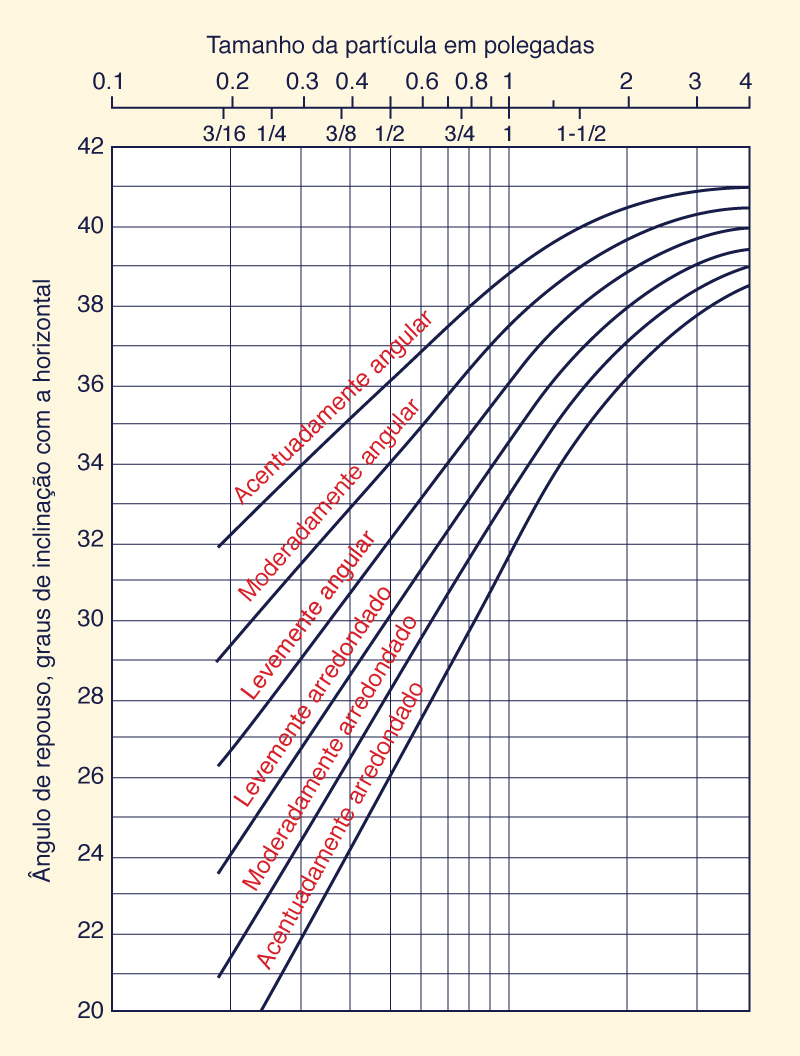A Figura 6-25 mostra o ângulo de repouso de materiais não coesivos, ou seja, o ângulo θ na Eq. 6-29. O tamanho das partículas (em polegadas) é aquele para o qual 25% do material (em peso) é maior. Fig. 6-25  Ângulo de repouso de materiais não coesivos (Chow, 1959). 6.4  TRAÇÃO ADMISSÍVEL [Outras Características]   [Questões]   [Problemas]   [Referências]   •   [Topo]   [Canais Não Erodíveis]   [Canais Erodíveis]   [Tração]   O método da força de tração admissível (força unitária ou tensão) é usado no projeto de canais e canais erosíveis. A força de tração admissível da unidade é a tensão máxima de cisalhamento que não causará erosão do material que forma o leito do canal em uma superfície nivelada. O valor, obtido a partir de experimentos de laboratório, é chamado de força de tração unitária crítica ou tensão de cisalhamento crítica. 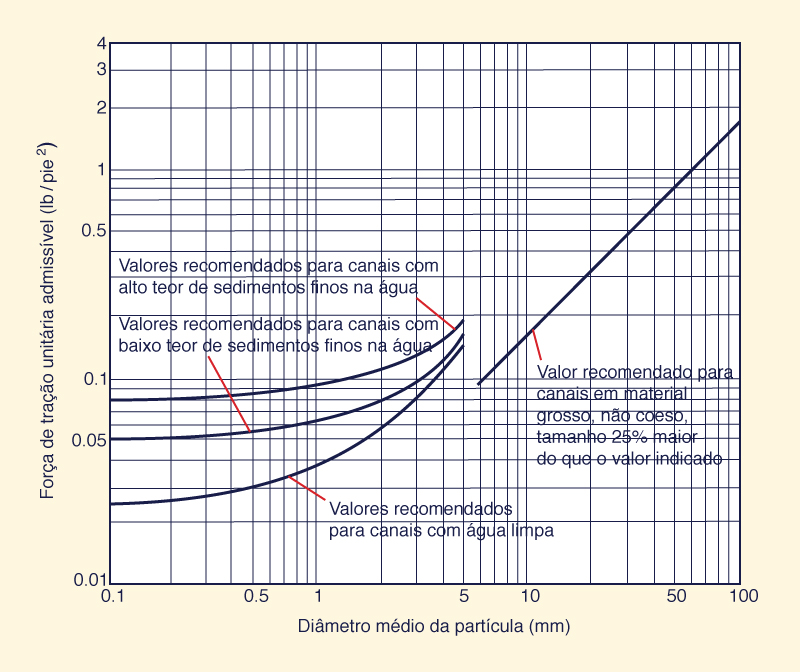A Figura 6-26 mostra a força de tração unitária admissível para canais em materiais não coesivos. A figura se aplica a uma faixa de diâmetro (médio) de partículas de 0,1 a 100 mm. O lado esquerdo do gráfico aplica-se a um material não coesivo fino (areia), com diâmetro variando de 0,1 a 5 mm. Três curvas são mostradas: A curva superior, aplicável a canais com alto teor de sedimentos finos (lodo) na água; A curva do meio, aplicável a canais com baixo teor de sedimentos finos na água; A curva inferior, aplicável a canais com água limpa. Observe que, quanto mais limpa a água, maior a probabilidade de captar sedimentos das margens e, portanto, menor é o valor da força de tração unitária admissível. O lado direito da Fig. 6-26 aplica-se aos canais com material grosso não coesivo, que possuem diâmetro variando de 5 a 100 mm (cascalho fino a muito grosseiro, até pequenas pedras). A linha mostrada na Fig. 6-26 é igual a 0,4 vezes o diâmetro da partícula (em polegadas) para o qual 25% do material é maior (em peso), ou seja, a força de tração admissível da unidade ou a tensão de tração admissível é igual a 0,4 × d25 (em polegadas). Fig. 6-26  Força de tração unitária admissível para canais com materiais não coesivos (Chow, 1959). 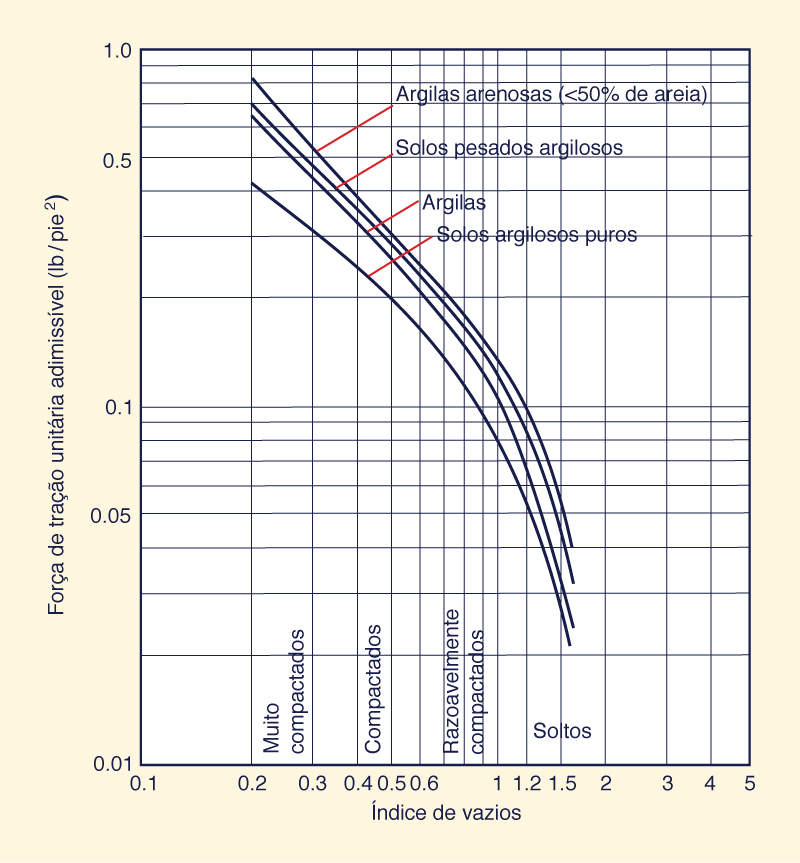Para materiais coesivos, a tensão crítica de cisalhamento é uma função do tipo de solo (argilas arenosas para argilas finas) e da proporção de vazios, conforme mostrado na Fig. 6-27. Fig. 6-27  Força de tração unitária admissível para canais com materiais coesivos (Chow, 1959). Os valores das Figs. 6-26 e 6-27 são aplicáveis para canais retilíneos. Para canais sinuosos, os valores mostrados nas figuras devem ser reduzidos, levando em consideração o escoamento superficial sobre as margens laterais do canal. A Tabela 6-2 mostra a redução percentual recomendada na tensão crítica de cisalhamento baseada na sinuosidade do canal. Tabela 6-2  Redução da tensão de cisalhamento crítica considerando a sinuosidade do canal. Sinuosidade Redução (%) Baixa 10 Moderada 25 Alta 40 Método de força de tração admissível O método da força de tração admissível é destinado aos projetos de canais erosíveis com base na tensão de cisalhamento crítica estimada para o(s) material (is) que constituem as margens limitantes do canal. O valor da tensão crítica de cisalhamento é determinado experimentalmente ou a partir da experiência do projetista. O procedimento computacional é descrito abaixo, juntamente com exemplos de dois casos possíveis: Uso do mesmo material nas laterais e no leito, e; Uso de um material nas laterais e outro na parte inferior. A. Mesmo material nas laterais e no leito Dados de entrada:   Vazão Q, declividade lateral z, declividade do canal S e n de Manning; partícula d25 e forma de grão; mesmo material nas laterais e no leito. Suponha b/y = 6, ou seja, um valor razoável para começar. Suponha que a força de tração nas laterais esteja controlando o projeto. Este é geralmente o caso quando o material nas laterais e no leito é o mesmo. Com b/y, use o gráfico da Fig 6-23 para determinar o valor de Cs (que é a ordenada do gráfico) na expressão referente à força de tração unitária atuante nas laterais: Ts = Cs γ y S. Com d25 e a forma do grão, use o gráfico da Fig. 6-25 para encontrar o ângulo de repouso θ. Calcule a inclinação lateral: φ = tan-1 (1/z). Use a Eq. 6-29 para calcular K. Use a Fig. 6-26 para determinar a força de tração unitária admissível no nível do terreno baseado no material de ambas as laterais τLs (na direita do gráfico), e a força de tração unitária admissível no nível do terreno baseado no material do leito τLb (na esquerda do gráfico). Calcule a força de tração unitária admissível nas laterais: τs = K τL. Defina a força de tração unitária admissível como sendo maior ou igual à força de tração unitária atuante: τs ≥ Ts; i.e., τs ≥ Cs γ y S Resolva a profundidade do fluxo: y = τs / (Cs γ S Calcule b: b = (b/y) y Com Q, b, z, n, e S conhecidos, resolva a profundidade normal yn. Teste para confirmar que yn ≤ y. Caso contrário, se o valor assumido de b/y for muito pequeno, assuma um valor maior e retorne à Etapa 11 para fazer nova iteração. Caso a premissa seja satisfeita, defina y = yn e vá para a próxima etapa. Com os últimos b/y e z, utilize o gráfico da Fig. 6-22 para determinar o valor de Cb (a ordenada do gráfico) na expressão da força de tração unitária atuante no nível do solo TL = Cb γ y S. . Calcule TL = Cb γ yn S Compare TL, calculado na Etapa 15 com τL calculado na Etapa 7. Se TL ≤ τL, as laterais controlam o projeto, como inicialmente assumido, finalizando assim o procedimento. A. Exemplo trabalhado Dados de entrada: Q = 600 cfs; z = 2, declividade do canal S = 0,001 e Manning n = 0,022; partícula d25 = 0,7 polegada e forma do grão levemente angular; mesmo material nas laterais e no leito. Suponha b/y = 6. Suponha que a força de tração nas laterais esteja controlando o projeto. Com b/y = 6 e z = 2, use gráfico da Fig. 6-23 para determinar o valor de Cs = 0,78. Com d25 = 0,7 e forma de grão levemente angular, use o gráfico da Fig. 6-25 para derivar θ = 34°. Calcule: φ = tan-1 (1/z) = 26.565° Use a Eq. 6-29 para calcular: K = 0,6. Use d25 = 0,7 polegadas no gráfico da Fig. 6-26 para determinar τL = 0,28 lb/pés2. Calcule: τs = K τL = 0,6 × 0,28 = 0,168 lb/pés2. Defina a força de tração unitária admissível como sendo maior ou igual à força de tração unitária atuante: τs = 0,168 ≥ Cs γ y S = (0,78) (62,4) y (0,001) Calcule a profundidade de fluxo: y ≤ 3,45 pés. Defina y = 3,45 como a profundidade do fluxo alvo. Calcule: b = (6) (3,45) = 20,7. Arredonde para b = 21 pés. Com Q = 600, b = 21, z = 2, n = 0,022, e S = 0,001, calcule a profundidade normal: yn = 4,536 pés. Sendo yn = 4,536 > y = 3,45. A largura b é muito pequena. Assuma (por tentativa e erro) b/y = 10. Assim, b = (10) (3,45) = 34,5. Arredonde para b = 35 pés. Com o novo b, calcule a profundidade normal: yn = 3,376 pés. Dessa forma, yn < y. Defina y = 3,376 pés e vá para o próximo passo. Com b/y = 10 e z = 2, use o gráfico da Fig. 6-22 para determinar o valor de Cb = 1,0. Calcule TL = (1,0) (62,4) (3,376) (0,001) = 0,211 lb/pés2. Compare o TL = 0,211 calculado na Etapa 15 com τL = 0,28 calculado na Etapa 7. Sendo TL = 0,211 < τL = 0,28, conclui-se que as laterais controlam o projeto, como inicialmente assumido. Assim, o procedimento é finalizado. B. Material distinto nas laterais e no leito Input data:  Vazão Q, declividade lateral z, declividade do canal S, e n de Manning; material distinto nas laterais e no leito, então, especifique o tipo de material, o tamanho das partículas e a forma dos grãos e, se necessário, o conteúdo de sedimentos finos. Assuma b/y = 6, um valor razoável para começar. Suponha que a força de tração nas laterais esteja controlando o projeto. Este é geralmente o caso quando o material nas laterais e no leito é o mesmo. Com b/y e z, use o gráfico da Fig. 6-23 para determinar o valor de Cs (Cs é a ordenada do gráfico) na expressão da força de tração uniária atuante nas laterais: Ts = Cs γ y S. Com d25 e forma do grão, use o gráfico da Fig. 6-25 para encontrar o ângulo de repouso θ. Calcule a declividade lateral: φ = tan-1 (1/z) Use a Eq. 6-29 para calcular K. Use o gráfico da Fig. 6-26 para determinar a força de tração unitária admissível no nível do solo baseada no material das laterais τLs (à direita do gráfico da Fig. 6-26), e a baseada no material do leito τLb (à esquerda do gráfico da Fig. 6-26). Calcule a força de tração unitária admissível nas laterais: τs = K τLs. Defina a força de tração unitária admissível é maior ou igual à força de tração unitária atuante: τs ≥ Ts; ou seja, τs ≥ Cs γ y S. Calcule a profundidade de fluxo: y = τs / (Cs γ S) Calcule b: b = (b/y) y Com Q, b, z, n, e S conhecidos, calcule a profundidade normal yn. Verifique se yn ≤ y. Caso contrário, o valor assumido para b/y é muito pequeno. Assuma então um valor maior e retorne para a Etapa 11 e faça uma iteração. Uma vez satisfeita a condição, defina y = yn e vá para a próxima etapa. Com os últimos b/y e z, use o gráfico da Fig. 6-22 para determinar o valor de Cb (ordenada do gráfico da Fig. 6-22) na expressão da força de tração unitária atuante no nível do solo TL = Cb γ y S. Calcule TL = Cb γ yn S Compare TL calculado na Etapa 15 com τLb calculado na Etapa 7. Se TL ≤ τL, as laterais controlam o projeto, conforme o que foi assumido inicialmente. Caso contrário, se TL > τL, o leito controla o projeto do canal. Se TL > τL, assuma TL = τL. Calcule o novo y, confirmando o controle do leito. B. Exemplo trabalhado Dados de entrada:  Q = 600 pés cúbicos/segundo; z = 2, declividade do canal S = 0,001 e Manning n = 0,022; material nas laterais: não coesivo, d25 = 0,7 polegada, forma do grão levemente angular; material no leitoo: não coesivo, d60 = 0,8 mm, com alto teor de sedimentos finos na água. Suponha que b/y = 6. Suponha que a força de tração nas laterais esteja controlando o projeto. Com b/y = 6 e z = 2, use o gráfico da Fig. 6-23 para determinar o vaor de Cs = 0,78. Com d25 = 0,7 polegadas e forma de grão levemente angular, use o gráfico da Fig. 6-25 para determinar θ = 34°. Calcule: φ = tan-1 (1/z) = 26,565° Use a Eq. 6-29 para calcular K = 0,6. Use o gráfico da Fig. 6-26 (à direita) para determinar τLs = 0,28 lb/pés2; use o gráfico da Fig. 6-26 (à esquerda) para determinar τLb = 0,09 lb/pés2. Calcule: τs = K τLs = 0,6 × 0,28 = 0,168 lb/pés2. Defina a força de tração unitária admissível para ser maior ou igual à força de tração unitária atuante: τs = 0,168 ≥ Cs γ y S = (0,78) (62,4) y (0,001) Calcule a profundidade do fluxo: y ≤ 3.45 pés. Calcule: b = (6) (3,45) = 20,7. Arredonde para b = 21 pés. Com Q = 600, b = 21, z = 2, n = 0,022, e S = 0,001, calcule a profundidade normal: yn = 4,536 pés. Calcule: yn = 4,536 > y = 3,45. A largura b é muito pequena. Suponha (por tentativa e erro) que b/y = 10. Sendo b = (10) (3,45) = 34,5, arredonde para b = 35 pés. Com o novo b, calcule a profundidade normal: yn = 3,376 pés. Agora yn < y. Defina que y = 3,376 pés e vá para a próxima etapa. Com b/y = 10 e z = 2, use o gráfico da Fig. 6-22 para determinar o valor de Cb = 1,0. Calcule TL = (1,0) (62,4) (3,376) (0,001) = 0,211 lb/pés2. Compare o vaor calculado de TL = 0,211 na Etapa 15 com o valor calculado de τLb = 0,09 na Etapa 7. Calcule: TL = 0,211 > τL = 0,09. Dessa forma, o leito controla o projeto. Assuma TL = Cb γ yn S = (1,0) (62,4) y (0,001) = 0,09. Portanto: y = 1,44 pés. Assuma (por tentativa e erro) que b/y = 106, resultando em: b = 154 pés. Com Q = 600, b = 152, z = 2, S = 0,001, e n = 0,022, calcule y = 1,44 ft. O projeto assim foi finalizado. 6.5  OUTRAS CARACTERÍSTICAS [Questões]   [Problemas]   [Referências]   •   [Topo]   [Canais Não Erodíveis]   [Canais Erodíveis]   [Tração]   [Tração Admissível]   Outros recursos no projeto de canais hidráulicos incluem quedas de canais e travessias de riachos, estruturas de dissipação e estruturas de controle de nível. As Figuras 6-28 a 6-34 mostram alguns exemplos ilustrativos. Fig. 6-28  Série de quedas de canais com o propósito de controlar a instabilidade do fluxo, no projeto de irrigação de Cabana-Mañazo, em Puno, Peru. Fig. 6-29  Travessia dos afluentes do canal de Tinajones através do córrego de Chiriquipe, em Lambayeque, Peru. Fig. 6-30  Pequena derivação no canal do córrego de Wellton-Mohawk, em Wellton, Arizona. Fig. 6-31  Travessia de canal por meio de galeria, no projeto de irrigação de Cabana-Mañazo em Puno, Peru. Fig. 6-32  Travessia do New River por meio tubulações, próximo de Calexico, no Vale Imperial, California. Fig. 6-33  Estrutura de dissipação, no Rio Mashcon, em Cajamarca, Peru. Fig. 6-34  Estruturas de controle de nível no Rio Caqueza, em Cundinamarca, Colômbia. QUESTÕES [Problemas]   [Referências]   •   [Topo]   [Canais Não Erodíveis]   [Canais Erodíveis]   [Tração]   [Tração Admissível]   [Outras Características]   O que determina a rugosidade da superfície em um canal artificial? Qual é a borda livre na concepção de um canal? Qual é a abcissa no diagrama Shields? Qual é a ordenada no diagrama Shields? Qual número de Froude geralmente garante o início do movimento? Como as velocidades mínimas e máximas admissíveis são tratadas em um projeto de canal? Como as velocidades máximas admissíveis e as tensões de cisalhamento estão relacionadas? Qual é o valor máximo do coeficiente Cs referente à tensão de cisalhamento nas laterais do canal? Qual é a faixa de ângulo de repouso de materiais não coesivos? Qual é a razão da força de tração? Como o conteúdo de sedimentos finos na água afeta o valor da força de tração unitária admissível? Quando uma estrutura de controle de nível é justificada? PROBLEMAS [Referências]   •   [Topo]   [Canais Não Erodíveis]   [Canais Erodíveis]   [Tração]   [Tração Admissível]   [Outras Características]   [Questões]   Qual é a velocidade mínima permitida para um diâmetro de partícula de sedimento ds = 0,6 mm e um fator de atrito adimensional de Chezy (Darcy-Weisbach modificado) f = 0,004? Qual é o número mínimo de Froude e a velocidade mínima admissível para um diâmetro do sedimento ds = 0,6 mm, fator de atrito adimensional f = 0,004, profundidade hidráulica D = 1 m e temperatura da água T = 20 ° C? Qual é o número mínimo de Froude e a velocidade mínima admissível para um diâmetro de sedimento ds = 0,3 mm, fator de fricção Chezy adimensional f = 0,003, profundidade hidráulica D = 3 pés e temperatura da água T = 68° F? Um canal possui os seguintes dados: Q = 330 pés cúbicos/segundo, z = 2, n = 0,025, e S = 0,0018. Use o método da força de tração para calcular a largura e a profundidade do leito nas seguintes condições: As partículas são iguais nas laterais e no leito; os sedimentos são moderadamente angulares e de tamanho d25 = 0,9 pol. O mesmo que em (a), mas as partículas são moderadamente arredondadas. Discuta como a forma das partículas afeta o projeto. Verifique com a ferramenta ONLINE TRACTIVE FORCE. Um canal possui os seguintes dados:   Q = 220 m3/s, z = 2, n = 0,03, e S = 0,0006. Use o método da força de tração para calcular a largura e a profundidade do leito nas seguintes condições: As partículas nas laterais são levemente angulares e de tamanho d25 = 35 mm; as partículas no leito são do tamanho d50 = 5 mm. As partículas nas laterais são as mesmas que em (a), mas as partículas no leito são menores, do tamanho d50 = 4 mm. Em ambos os casos (a) e (b), há baixo conteúdo de sedimentos finos na água e a sinuosidade do canal é insignificante. Discuta como o tamanho da partícula no leito afeta o projeto. Verifique com a ferramenta ONLINE TRACTIVE FORCE. Um certo tipo de grama tem tensão de cisalhamento crítica τc = 30 N/m2.fator de atrito adimensional de Chezy f = 0,0075. Qual é uma boa estimativa da velocidade crítica? REFERÊNCIAS •   [Topo]   [Canais Não Erodíveis]   [Canais Erodíveis]   [Tração]   [Tração Admissível]   [Outras Características]   [Questões]   [Problemas]   American Society of Civil Engineers, 1975. Sedimentation Engineering. Manual of Practice No. 54. Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, New York. Ponce, V. M. 1989. Engineering Hydrology, Principles and Practices. Prentice Hall, Englewood Cliffs, New Jersey. http://ponce.sdsu.edu/canais/index.html 200626 08:00