|
|
|
CAPÍTULO 8: HIDRÁULICA DE GALERIAS DE DRENAGEM DE ÁGUAS PLUVIAIS |
8.1 GALERIAS DE DRENAGEM DE ÁGUAS PLUVIAIS
|
|
As galerias de drenagem de águas pluviais são condutos de drenagem hidraulicamente curtos, colocados em locais onde a rede de drenagem cruza a rede de transporte (estradas, trilhos). Galerias de drenagem de águas pluviais diferem das pontes por serem muito menores; assim, há muito mais bueiros do que pontes. As galerias de drenagem de águas pluviais são projetadas para operar sob fluxo gradualmente variado. Portanto, os princípios do Capítulo 7 são aplicáveis.
As galerias de drenagem de águas pluviais são projetadas para passar a vazão do projeto sem ultrapassar a superestrutura. A vazão do projeto é derivada da chuva de projeto, que é baseada em considerações hidrológicas. O período de retorno (recíproco da frequência) varia tipicamente de 10 a 50 anos (Ponce, 2008). Quanto maior o período de retorno, maior a vazão do projeto e, portanto, maior o tamanho da galeria necessária (Fig. 8-1).
|
O fluxo em uma galeria é uma função de:
Tamanho e forma da seção transversal,
Declividade do leito (inferior),
Comprimento da galeria,
Rugosidade, e
Características de entrada e saída.
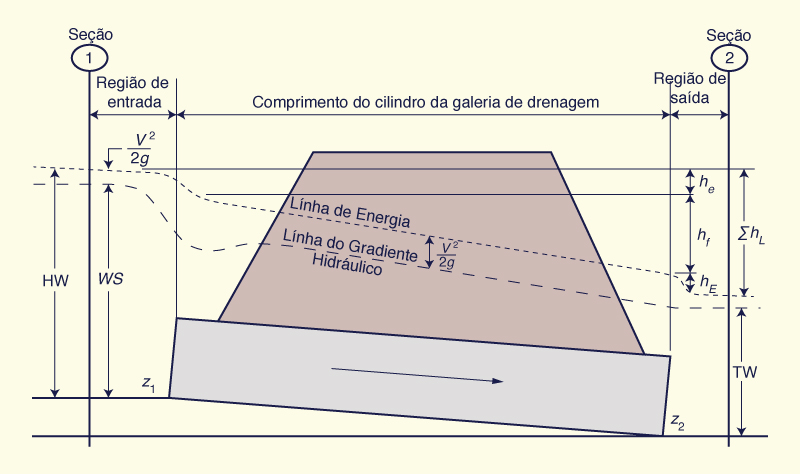
O fluxo em uma galeria pode ser em: (a) superfícies completamente livres (fluxo de canal aberto); (b) condutos completamente fechados; (c) escoamentos parcialmente superficiais e de condutos fechados parcialmente. Nível da água na cabeceira (HW ) é a profundidade invertida da água na entrada da galeria. Nível de água na cauda (TW ) é a profundidade invertida da água acima da galeria na saída. As elevações de projeto da cabeceiras e da cauda são fatores importantes para determinar se a galeria flui parcialmente ou completamente cheia.
O objetivo é desenvolver um projeto mais econômico (ou seja, o menor tamanho de bueiro ou galeria) que passará na vazão do projeto sem exceder a elevação especificada da cabeceira
|
8.2 CONTROLE NA ENTRADA
|
|
O fluxo da galeria está sob controle de entrada quando a vazão depende apenas das condições na entrada. Por exemplo, suponha uma galeria circular de diâmetro D, comprimento L, inclinação S, profundidade na cabeceira HW e profundidade da água na cauda TW.
O primeiro passo é calcular a profundidade normal yn e a profundidade crítica do fluxo yc.
Se yn < yc , o fluxo na galeria é supercrítico e a água da cauda não tem influência nas condições à montante (Fig. 8-3). Portanto, a cabeceira é controlada exclusivamente pelas condições na entrada.
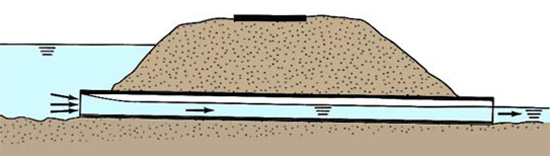
Fig. 8-3 Fluxo da galeria sob condições supercríticas, com entrada submersa e saída não submersa.
Se o fluxo for supercrítico e o TW > yn , um ressalto hidráulico pode se formar na saída da galeria ou próximo da mesma (Fig. 8-4).
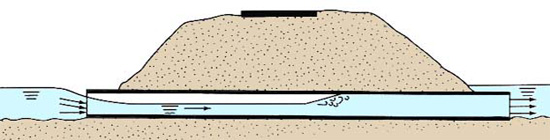
Fig. 8-4 Fluxo da galeria sob condições supercríticas, com entrada não submersa e saída submersa.
O controle de entrada ocorre quando o tubo da galeria é capaz de transportar mais vazão do que a entrada. A seção de controle está localizada logo abaixo da entrada do bueiro. O fluxo passa através da profundidade crítica na seção de controle e se torna supercrítico à jusante da entrada.
Sob controle da entrada, a galeria atua como um orifício ou açude. Se a entrada estiver submersa, a condição de fluxo se assemelha à de um orifício; se a entrada não for submersa, a condição de fluxo será semelhante à de um açude. [Se HW < 1,2 D, então a entrada não será submersa]. Se a entrada não for submersa, mas a saída for submersa, um ressalto hidráulico se formará dentro do tubo da galeria.
8.3 CONTROLE NA SAÍDA
|
|
O controle de saída ocorre nas seguintes condições:
Quando TW > 1,2 D, ou seja, para um alto nível de água na cauda. Nesse caso, o tubo da galeria estará completamente cheio de água, semelhante ao fluxo de condutos fechados.
O nível de água da cabeceira pode ser calculado aplicando a equação de energia da elevação do conjunto à montante (u/s) à elevação do conjunto à jusante (d/s).O nível de água na cabeceira é determinado diretamente pela elevação da água na cauda e pelas características de atrito do tubo da galeria.-
Quando a entrada e a saída estão submersas.
-
Quando a declividade da galeria é branda (fluxo sub-crítico) e o nível de água da cabeceira e da cauda é menor que o diâmetro da galeria (HW < D; TW < D ). Nesse caso, a melhor abordagem é calcular o perfil da superfície da água.
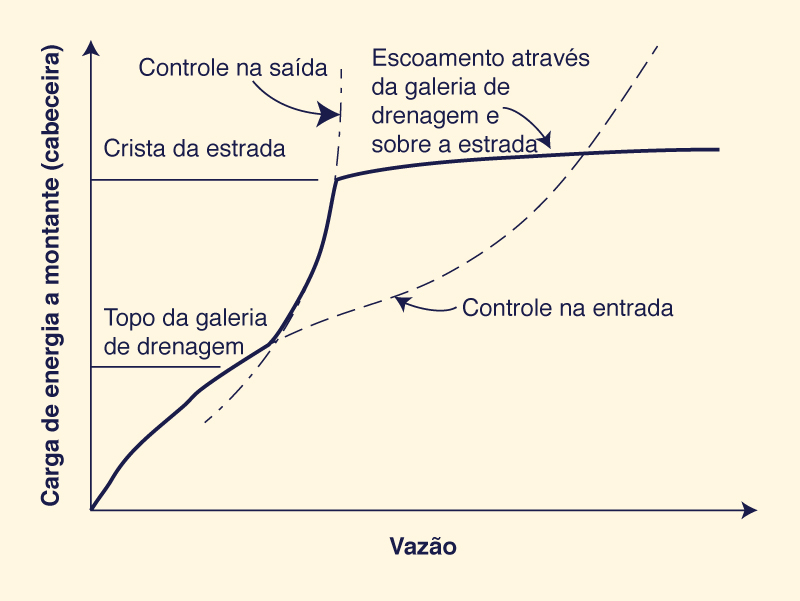
A Figura 8-5 mostra um desenho esquemático da vazão em função da energia da cabeceira sob controle de entrada e saída (US Army Corps of Engineers, 2014). Observe que, à medida que a vazão aumenta de baixa para alta, em um determinado nível, o fluxo muda bruscamente mais ou menos do controle de entrada para o controle de saída.
|
8.4 PROJETO DE GALERIAS DE DRENAGEM DE ÁGUAS PLUVIAS
|
|
As etapas a seguir são seguidas no projeto da galeria:
Agrupar os dados do projeto
Vazão,
Nível da água da cauda e
Declividade do tubo da galeria.
Escolha as características da galeria
Forma de seção transversal (circular, quadrada, retangular, arco),
Dimensões (diâmetro, se circular),
Comprimento do tubo,
Tipo de material (Fig. 8-6 e 8-7) (concreto, aço corrugado, alumínio corrugado, alvenaria de pedra) e
Tipo de entrada (de arestas quadradas ou arredondadas).

Fig. 8-6 Conjunto de duas galerias feitas de aço corrugado.
Verifique o tipo de controle predominante (entrada ou saída), com base no (a) nível da água na cabeceira, (b) nível da água na cauda, (c) diâmetro e (d) declividade.
Se o controle de entrada prevalecer, calcule a elevação necessária da cabeceira para passar na vazão de projeto.
Se o controle da saída prevalecer, calcule a elevação da cabeceira necessária usando
(a) a equação da energia ou (b) os cálculos do perfil da superfície da água.Se o nível da água da cabeceira for maior que o permitido, escolha uma galeria de tamanho maior e repita o processo.
Em alguns casos, pode não ser possível determinar o tipo de controle a priori. Nesse caso, os dois cálculos são recomendados. O tipo de controle de projeto é aquele que resulta na maior elevação da cabeceira.
Outras considerações para os projetos de galerias:
Tubulação no aterro ao redor da galeria,
Limpeza local na saída das galerias,
Erosão do material de preenchimento próximo à entrada,
Entupimento com detritos excessivos e
Provisão de passagem para peixes.
|
|
Exemplo de projeto
Projete uma galeria com as seguintes condições:
Solução
|
QUESTÕES
|
|
O que é uma galeria?
Qual é o período de retorno típico para o projeto de galerias de drenagem de águas pluviais?
Quando uma galeria está sob controle de entrada?
Quando uma galeria está sob o controle de saída?
Liste as variáveis hidráulicas que afetam o fluxo da galeria.
Liste outras considerações no projeto de galerias.
PROBLEMAS
|
|
Projete uma galeria circular de concreto com os seguintes dados: Q = 300 pés3/s; elevação invertida na entrada z1 = 100 pés; profundidade da água na cauda y2 = 4 pés; declividade da tubulação So = 0,02; comprimento do tubo L = 200 pés; n de Manning = 0,013; elevação do acostamento da rodovia Es = 112 pés; borda livre à montante Fb = 2 pés. O tipo de entrada é uma aresta quadrada com paredes laterais (Fig. 8-10). Use CANAL EMLINHA 06 para calcular a profundidade normal e CANAL EMLINHA 07 para calcular a profundidade crítica na galeria.

Fig. 8-10 Típica passagem de uma galeria.
Projete uma galeria circular de concreto com os seguintes dados: Q = 500 cfs; elevação invertida na entrada z1 = 100 pés; profundidade da água na cauda y2 = 4 pés; declividade da tubulação So = 0,01; comprimento da tubulação L = 200 pés; n de Manning = 0,013; elevação do acostamento da rodovia Er = 115 pés; borda livre à montante Fb = 2 pés. O tipo de entrada é uma borda quadrada com paredes laterais. Use CANAL EMLINHA 06 para calcular a profundidade normal e CANAL EMNLINHA 07 para calcular a profundidade crítica na galeria. Verifique o projeto da galeria usando EMLINHA GALERIAS.
REFERÊNCIAS
|
|
Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, New York.
Ponce, V. M. 2008. Questões e respostas sobre o período de retorno que deve ser usado em projetos. Online article.
Roberson, J. A., J. J. Cassidy, e M. H. Chaudhry. 1998. Hydraulic Engineering, Second edition, Wiley.
U.S. Army Corps of Engineers. 2018. HEC-RAS River Analysis System. Version 5.0.5, Hydrologic Engineering Center, Davis, California.
| http://ponce.sdsu.edu/canais/index.html |
|
200626 08:00 |