[Vertedouro de soleira delgada]   [Forma da soleira do vertedouro de lâmina livre]   [Curva-chave de vertedouros]   [Ressalto Hidráulico]   [Questões]   [Problemas]   [Referências]   •   CAPÍTULO 9: ESCOAMENTO ESTÁVEL RAPIDAMENTE VARIADO 9.1  VERTEDOURO DE SOLEIRA DELGADA [Forma da soleira do vertedouro de lâmina livre]   [Curva-chave de vertedouros]   [Ressalto Hidráulico]   [Questões]   [Problemas]   [Referências]   •   [Topo]   O fluxo rapidamente variado difere do fluxo gradualmente variado (capítulo 7) na maior curvatura das linhas de corrente. Em casos extremos, o fluxo é praticamente interrompido, resultando em altos níveis de turbulência e perda de energia associada. As seguintes características descrevem o fluxo variado rapidamente: A curvatura das linhas de corrente é tão pronunciada que a distribuição de pressão não pode ser considerada hidrostática. Diferentemente do fluxo gradualmente variado, as mudanças nas variáveis de fluxo ocorrem a uma distância relativamente curta (Fig. 9-1). O atrito limite é pequeno comparado às outras forças e geralmente é insignificante. As características do fluxo são fixadas pela geometria de contorno geralmente rígida. Os coeficientes de distribuição de velocidade α e β são muito maiores que a unidade (1) e não podem ser determinados com precisão. As zonas de separação, redemoinhos e rolos tendem a complicar o padrão de fluxo, com o fluxo geralmente confinado às zonas de separação. Até o momento, não há solução teórica para fluxo variado rapidamente. Em vez da teoria, as relações empíricas são usadas em muitas aplicações. Fig. 9-1  Queda de um canal com exemplo típico de fluxo variado rapidamente. Vertedouro de soleira delgada O vertedouro de soleira delgada é um dispositivo de medição em fluxo de canais (Capítulo 4). É também a forma mais simples de vertedouro destinado ao transbordamento. O perfil do vertedouro pode ser feito para coincidir com a forma da superfície inferior da lâmina de escoamento. A forma da lâmina de escoamento pode ser interpretada pelo princípio do projétil (Chow, 1959) (Fig. 9-2). 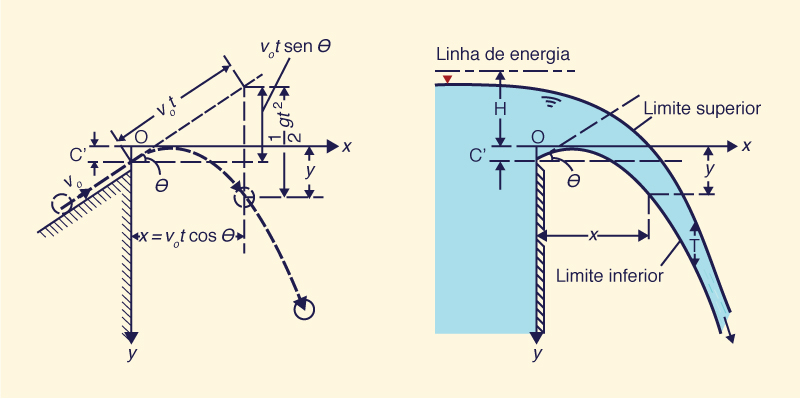De acordo com esse princípio, o componente de velocidade horizontal do fluxo é constante, e a única força que atua sobre a lâmina é a força gravitacional. No tempo t, uma partícula de água na superfície inferior da lâmina de escoamento percorrerá uma distância horizontal x (à frente do vertedouro) igual a: Fig. 9-2 Perfis da lâmina sobre um vertedouro de soleira delgada pelo pelo princípio do projétil (Chow, 1959). x = vo t cos θ (9-1) Ao mesmo tempo, a partícula percorrerá uma distância vertical y igual a: y = - vo t sin θ  +  (1/2) g t 2  +  C' (9-2) Em que:   g = aceleração gravitacional;                 C' = valor de y em x = 0. A constante C' pode ser tomada como a distância vertical entre o ponto mais alto da lâmina e a elevação da soleira. Eliminando t das Eqs. 9-1 e 9-2:   y                x                  x      ____  =  A (____)2  +  B (____)  +  C   H              H                  H          (9-3) Em que:                   g H                                 A  =  ________________            2 vo2 cos2 θ                        (9-4)                                                   B  =  - tan θ                                    (9-5)             C'                                 C  =  ______             H   (9-6) Assumindo a espessura vertical da lâmina T, um termo adicional pode ser adicionado à Eq. 9-5 para obter a equação da lâmina d'água:   y                x                  x      ____  =  A (____)2  +  B (____)  +  C  +  D   H              H                  H          (9-7) Em que:   D = T / H . Descarga do vertedouro de soleira delgada Uma fórmula comum para a vazão sobre um vertedouro de soleira delgada é: Q = C L H 3/2 (9-8) Em que:   C = coeficiente de descarga;                 L = comprimento efetivo da soleira do vertedouro;                 H = carga medida acima do vertedouro, excluindo a carga de velocidade. Os coeficientes de descarga para vários tipos de vertedouros de soleira delgada são apresentados no Capítulo 4. 9.2  FORMA DA SOLEIRA DO VERTEDOURO DE LÂMINA LIVRE [Curva-chave de vertedouros]   [Ressalto Hidráulico]   [Questões]   [Problemas]   [Referências]   •   [Topo]   [Vertedouro de soleira delgada]   A forma do vertedouro mostrada na Fig. 9-3 é referida como uma forma ogee, porque se assemelha a uma curva com a forma de um S, consistindo em dois arcos que se curvam em lados opostos, de modo que as extremidades são aproximadamente paralelas. Na prática, não obstante à forma da barragem, pressões negativas podem se desenvolver em um vertedouro ogee. Pressões negativas excessivas podem causar danos à cavitação e, portanto, devem ser controladas. Fig. 9-3 (a)  Vertedouro de emergência do reservatório Turner, em San Diego, California, EUA (sem transbordamento). Fig. 9-3 (b)  Vertedouro de emergência do reservatório Turner, em San Diego, California, EUA (com transbordamento em 24 de fevereiro de 2005). 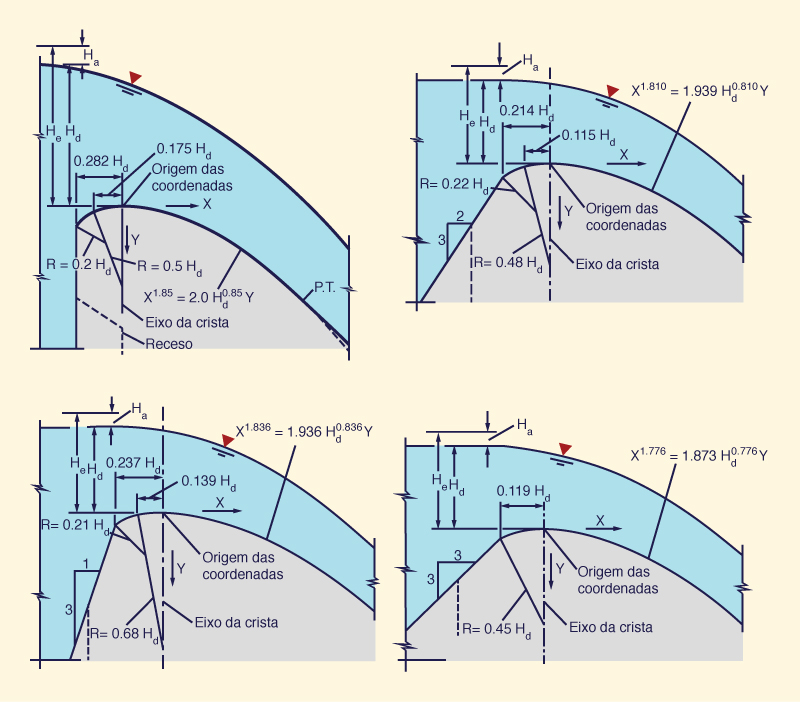Formas de vertedouro WES O Corpo de Engenheiros do Exército dos EUA desenvolveu várias formas padrão em sua Estação Experimental de Hidrovias. Essas formas, mostradas na Fig. 9-4, são chamadas de formas padrão de vertedouro WES. Fig. 9-4  Formas típicas do vertedouro WES (Chow, 1959). As formas WES seguem a equação: X n  =  K Hd n-1 Y (9-9) Em que:   X e Y = são as coordenadas do perfil da soleira, com a origem das coordenadas no ponto                               mais alto da mesma;                 Hd       = carga de projeto, excluindo a o cabeçote de velocidade do fluxo de aproximação;                 K e n   = são parâmetros que dependem da declividade frente à montante. Os valores de K e n são mostrados na Tabela 9-1. Para valores intermediários, a interpolação é possível. Tabela 9-1  Valores de K e n (Eq. 9-9). Declividade face   à montante K n Vertical 2,000 1,850 3V:1H 1,936 1,836 3V:2H 1,939 1,810 3V:3H 1,873 1,776 Às vezes, a face à montante do vertedouro pode ser projetada para recuar, como mostrado pelas linhas tracejadas da Fig. 9.4. O recuo não afetará a forma da soleira, desde que a modificação comece com pelo menos na metade da carga total He abaixo da origem. Abaixo dessa profundidade, as velocidades verticais são pequenas e o efeito correspondente no perfil da lâmina é insignificante. Para formas WES, a descarga sobre o vertedouro é: Q  =  C L He 3/2 (9-10) Em que:   H e = carga de energia total na soleira, incluindo a carga de velocidade no canal de acesso. 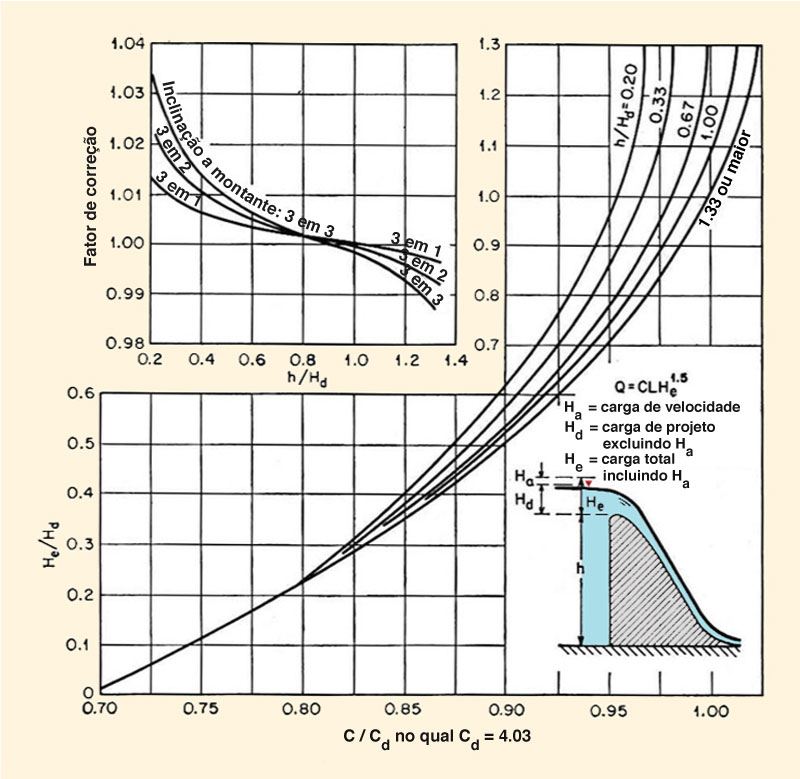O teste do modelo mostrou que o efeito da velocidade de aproximação é desprezível quando a altura h do vertedouro é superior a 1,33 Hd , onde Hd = carga de projeto, excluindo a velocidade de aproximação. Sob essa condição, o coeficiente de descarga, em unidades habituais nos EUA, é Cd = 4,03. Para vertedouros baixos, onde h/Hd < 1,33, a velocidade de aproximação terá um efeito apreciável na vazão e, portanto, no perfil da lâmina. A Figura 9-5 mostra o efeito da velocidade de aproximação na relação entre (He /Hd) e (C /Cd) para vertedouros WES com uma face vertical à montante. Na Figura 9-5, para h /Hd ≥ 1,33 e He > Hd, a relação C/Cd > 1. Observa-se que a razão C/Cd varia de 0,70 próximo ao nível da soleira (He /Hd ≅ 0) a 1,05 para He /Hd > 1,3. Assim, efetivamente, C varia de 2,82 a 4,23 (unidades habituais nos EUA). Para uma face inclinada à montante, C é multiplicado pelo fator de correção mostrado no lado superior esquerdo da Fig. 9-5. Fig. 9-5  Relação carga-descarga para as formas do vertedouro padrão do tipo WES (Chow, 1959). 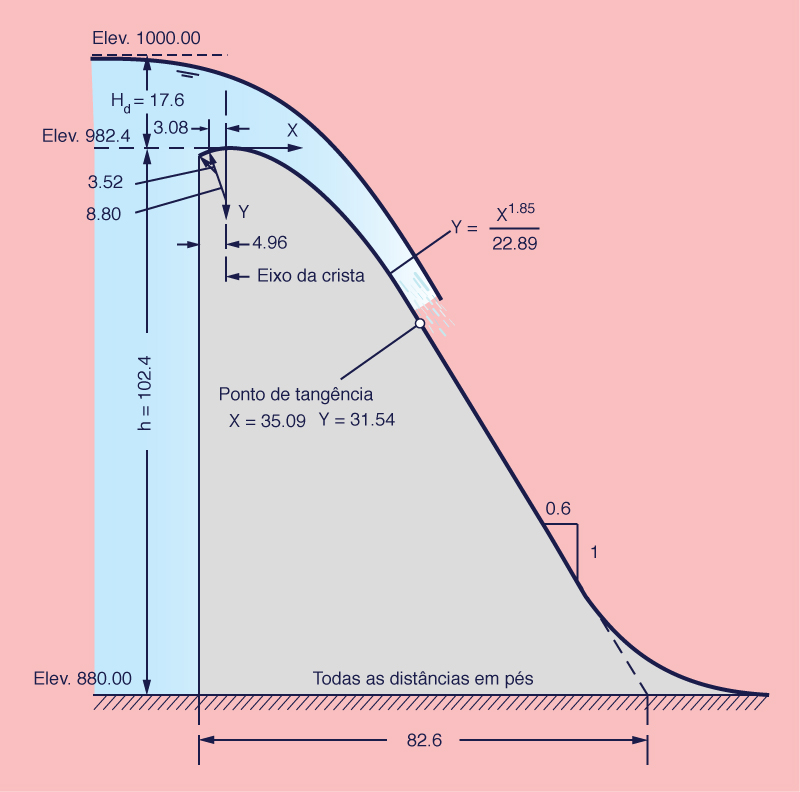Vertedouro WES:  Exemplo de projeto Determine a elevação da soleira e a forma de uma seção do vertedouro de transbordamento (forma padrão do vertedouro WES) com uma face vertical à montante e um comprimento de soleira L = 250 pés. A vazão de projeto é Q = 75.000 pés3/s. A superfície da água à montante, na descarga do projeto está na altitude de 1.000 pés, enquanto o piso do canal está na altitude de 880 pés (Fig. 9-6). Fig. 9-6  Desenho esquemático da seção de um vertedouro de transbordamento (Chow, 1959). Solução Suponha um vertedouro de alto transbordamento, para o qual o efeito da velocidade de aproximação é insignificante. Então: Hd = He, e C = 4,03. h + Hd = 1000 - 880 = 120 pés. From Eq. 9-10: Q = C L He3/2 Portanto, a carga de energia total, incluindo a carga de velocidade, é:  He = 17,7 pés. A velocidade de aproximação é: Va = Q / [L (h + Hd ) ] = 75,000 / [(250) (120)] = 2,5 pés3/s. A carga de velocidade é: Ha = Va 2 / (2 g ) = 2,5 2 / (2 × 32,17) = 0,097 ≅ 0,1 A carga de projeto, excluindo a carga de velocidade, é: Hd = He - Ha = 17,7 - 0,1 = 17,6 pés. A altura da barragem é: h = 120 - 17,6 = 102,4 pés. h = 102,4  >  1,33 Hd  =  23,4 pés. Portanto, o efeito da velocidade de aproximação é insignificante. A elevação da soleira é: 1000 - 17,6 = 982,4 pés. Da Eq. 9-9 e Tabela 9-1: X 1,85 = 2 Hd 0,85 Y Portanto, a equação da lâmina é: Y  =  X 1,85 / (22,89) Para calcular as coordenadas do ponto de tangência (Fig. 9-6): Y'  =  (1,85 / 22,89) X 0,85  =  0,081 X 0,85 Y'  =  = ΔY /ΔX = 1/0,6 = 1,667 1,667  =  0,081 X 0,85 Resolvendo para a abcissa do ponto de tangência: X = 35,09 pés.   RESPOSTA. Resolução para a ordenada do ponto de tangência (Fig. 9-6): Y = X 1,85 / (22,89) = 31,54 pés.   RESPOSTA. O comprimento da base, projetado a partir do ponto de tangência em uma declividade de 1V:0,6H até a base da barragem (veja as Figuras 9-4 e 9-6) é: Lb  =  0,282 Hd  +  X  +  (0,6) (h - Y ) Lb  =  [ 0,282 (17,6) ]  +  35,09  +  [ (0,6) (102,4 - 31,54) ] Lb  =  82,6 pés.  RESPOSTA. 0,282 Hd = 4,96 pés.  RESPOSTA. 0,175 Hd = 3,08 pés.  RESPOSTA. 0,2 Hd = 3,52 pés.  RESPOSTA. 0,5 Hd = 8,80 pés.  RESPOSTA. Vertedouros do tipo Ogee A Figura 9-7 mostra vários vertedouros do tipo ogee. Esse tipo de vertedouro é preferido para barragens altas, porque seu coeficiente de descarga (C = 4,03 em unidades habituais nos EUA e C = 2,22 em unidades SI) é substancialmente mais alto que o valor teórico para barragens com soleira espessa ( C = 3,087 em unidades habituais nos EUA e C = 1,704 em unidades SI) (Capítulo 4 - Controle de escoamento crítico). Fig. 9-7 (a)  Vertedouro emergencial da Represa El Capitan, no Rio San Diego, em San Diego, Califórnia, EUA. Fig. 9-7 (b)  Vertedouro emergencial da Represa Mangla, no Rio Jhelum, Paquistão. Fig. 9-7 (c)  Vertedouro emergencial da Represa Oroville, no Rio Feather, próximo de Oroville, Califórnia, EUA. Vertedouros de soleira espessa A Figura 9-8 mostra dois vertedouros de soleira espessa. O que tem 8000 pés de comprimento (vertedouro de emergência) da área de convervação de Boerasirie, mostrada na Fig. 9-8 (a), foi projetado com coeficiente de descarga que varia de C = 1,45 no nível do derramamento a C = 1,78 na carga de projeto Hd = 0,215 m (coeficiente de descarga em unidades SI). A barragem de Villa Grande, mostrada na Fig. 9-8 (b), é um reservatório de armazenamento fora da área de fluxo, com uma pequena área de drenagem contribuinte. Portanto, não são esperadas grandes inundações e o açude de soleira espessa é considerado suficiente para lidar com a vazãoo de pico do projeto. Fig. 9-8 (a)  Vertedouro de emergência na área de convervação de Boerasirie, em Guiana. Fig. 9-8 (b)  Vertedouro de transbordamento da represa de Villa Grande, em Cuajone, Peru. Vertedouros labirinto O vertedouro labirinto é usado para aumentar o comprimento efetivo da soleira, quando consideradoum aumento do risco devido às falhas hidrológicas. A Figura 9-9 mostra três exemplos de vertedouros labirinto. O labirinto funciona bem no estágio de projeto acima da soleira do vertedouro. No entanto, para estágios superiores ao de projeto, o comprimento efetivo acaba se reduzindo ao comprimento real e o labirinto deixa de fornecer a vantagem desejada. Fig. 9-9 (a)  Lagoa de Valentine Mill, em Valentine, Nebraska, EUA. Fig. 9-9 (b)  Bacia de detenção da Baixa Las Vegas, Nevada, EUA. Fig. 9-9 (c)  Barragem de Ute, Novo México, EUA. Vertedouros fusíveis Um vertedouro ou dique fusível é um aterro projetado para que o fluxo possa ocorrer até um nível superior de maneira previsível e controlada quando é necessário que uma capacidade se exceda para um vertedouro de serviço e durante eventuais obras de saída (Pugh e Gray, 1984). De acordo com o U.S. Bureau of Reclamation dos EUA, os projetos de diques fusíveis tem sido utilizados nas barragens de Bartlett e Horseshoe, no Rio Verde, Arizona. O vertedouro fusível da barragem Bartlett é projetado com uma estrutura de pilar invertido resistente à erosão para uma capacidade superior a 10.100 m3/s. Três seções de aterro erodíveis funcionarão em sequência. O vertedouro fusível da Horseshoe Dam foi projetado para uma capacidade superior a 6.850 m3/s por três aberturas de 44 a 52 m de comprimento, com 6,0 a 7,9 m de altura. Fig. 9-10  Vertedouro fusível no Rio La Leche, em Lambayeque, Peru. Outros recursos de vertedouros Outras características do vertedouro incluem vertedouros com vedação de borracha (Fig. 9-11), vertedouros de salto-esqui (Fig. 9-12) e estruturas de dissipação com defletores (Fig. 9-13). Fig. 9-11  Vertedouro com vedação de borracha, na bacia de retenção do Arroyo Pasajero, próximo de Coalinga, Califórnia. Fig. 9-12  Vertedouro de salto-esqui, na represa de Oros, Rio Jaguaribe, Ceará, Brasil. Fig. 9-13  Estrutura de dissipação com defletores, na represa de Gallito Ciego,em La Libertad, Peru. Incidente do vertedouro de Lake Oroville Em fevereiro de 2017, o controle de inundações e os vertedouros de emergência no lago Oroville, no norte da Califórnia, falharam depois que 12,8 polegadas de chuva que ocorreu entre 6 e 10 de fevereiro na bacia do rio Feather. A linha do tempo dos eventos que levaram à falha está documentada no vídeo "Linha do tempo do incidente do derramamento no Lago Oroville" (Lake Oroville Spillway Incident Timeline). Em setembro de 2018, o custo de reparos e outros problemas decorrentes da falha haviam subido para US $ 1,1 bilhão. Fig. 9-14  Situação posterior à falha no vertedouro de controle de inundações do Lago Oroville, norte da Califórnia, EUA. 9.3  CURVA-CHAVE DE VERTEDOUROS [Ressalto Hidráulico]   [Questões]   [Problemas]   [Referências]   •   [Topo]   [Vertedouro de soleira delgada]   [Forma da soleira do vertedouro de lâmina livre]   Na vazão de projeto, a pressão na soleira do vertedouro é próxima da atmosférica. A carga de projeto HD, que inclui a carga de velocidade, corresponde à descarga do projeto. Taxas de vazão inferiores à taxa de fluxo projetada produzirão pressões na face do vertedouro acima da pressão atmosférica, enquanto taxas de vazão maiores que a taxa de fluxo projetada produzirão pressões subatmosféricas. 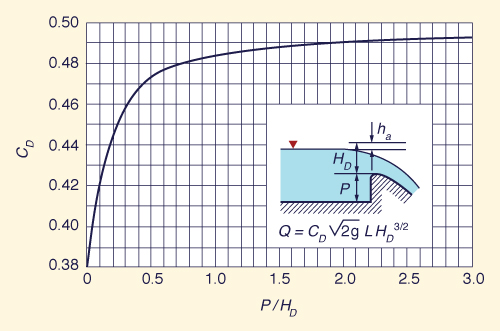A vazão de um vertedouro de ogee não fechado pode ser calculada da seguinte forma (Roberson et al., 1998): QD  =  CD (2 g)1/2 L HD 3/2 (9-11) Em que:  QD = vazão de projeto;                 CD = coeficiente de descarga de projeto adimensional;                 L = comprimento da soleira perpendicular ao fluxo;                 HD = carga de projeto total na soleira, incluindo a carga develocidade de aproximação ha . A Figura 9-15 mostra os valores de CD em função de P/HD, nos quais P = altura da soleria do vertedouro medida a partir do leito do canal. Observe que, para valores grandes de P/HD, o valor de CD se aproxima assintoticamente de um valor de CD = 0,492. Em geral, a vazão em vertedouros do tipo ogee é: Q  =  C (2 g)1/2 L H 3/2 (9-12) Em que:   Q = vazão;                 C = coeficiente de descarga adimensional; ,               L = soleira de comprimento perpendicular ao escoamento;                 H = carga na soleira incluindo a carga da velocidade de aproximação. Fig. 9-15  Variação do coeficiente de descarga CD com o comprimento relativo da barragem P/HD (Roberson et al., 1998). 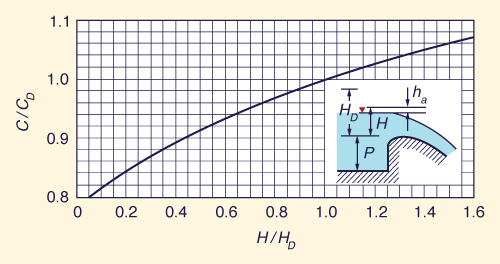A razão C/CD varia em função de H/HD, como mostrado na Fig. 9-16. As Figuras 9-15 e 9-16 podem ser usadas para desenvolver uma curva-chave de um vertedouro, ou seja, uma relação entre a vazão Q e a carga acima da soleira H do vertedouro . Se a carga real H exceder a carga de projeto HD, as pressões subatmosféricas se desenvolverão no vertedouro, e isso poderá causar danos por cavitação. Para evitar danos por cavitação, a carga de pressão negativa deve ser mantida a uma distância de -20 pés. Fig. 9-16  Variação do coeficiente de vazão adimensional C/CD com altura relativa sobre o nível da soleira H /HD (Roberson et al., 1998). 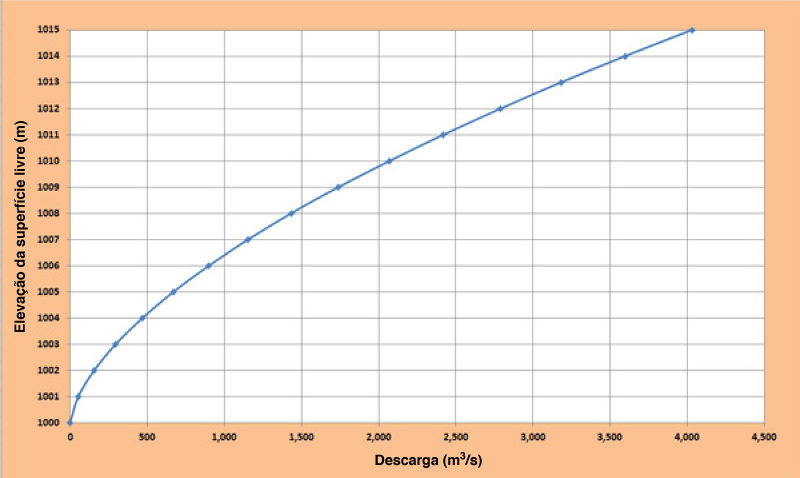Curva-chave do vertedouro: Exemplo Determine a curva-chave de um vertedouro do tipo ogee com comprimento L = 30 m. A carga de projeto é: HD = 10 m. O bordo livre é: Fb = 5 m. A elevação da soleira do vertedouro é de 1.000 m. A elevação do leito do rio é de 970 m. Desconsidere a velocidade de aproximação. Solução L = 30 m. P = 1000 - 970 = 30 m. P /HD = 30 / 10 = 3 Da Fig. 9-14, para P /HD = 3:  CD = 0,493 A equação da curva-chave do vertedouro é Eq. 9-12: Q  =  C (2 g )1/2 L H 3/2 Q  =  C (2 × 9,806)1/2 (30) H 3/2 Q  =  132,856 C H 3/2 A equação de classificação do vertedouro é: Q  =  132,856 C H 3/2  RESPOSTA. Os cálculos estão resumidos na Tabela 9-2. A coluna 1 mostra as elevações postuladas da superfície da água, desde a elevação da soleira (1.000 m) até a elevação de projeto da superfície da água (1.010 m) para uma elevação da superfície da água que inclui a bordo livre (1.015 m). A coluna 2 mostra a carga real sobre a soleira do vertedouro. A coluna 3 mostra as razões H /HD. A coluna 4 mostra as proporções C /CD, obtidas da Fig. 9-15. A coluna 5 mostra valores de C = CD (C /CD) = 0,493 (C /CD) A coluna 6 mostra os valores de Q calculados com a equação da curva-chave do vertedouro: Q  =  132,856 C H 3/2 A curva-chave do vertedouro é mostrada na Fig. 9-17. Tabela 9-2 Cálculo da curva-chave do vertedouro. [1] [2] [3] [4] [5] [6] Elevação (m) H (m) H /HD C /CD C Q (m3/s) 1000 0 0,0 0,780 0,385 0,000 1001 1 0,1 0,811 0,400 53,119 1002 2 0,2 0,842 0,415 155,986 1003 3 0,3 0,869 0,428 295,584 1004 4 0,4 0,895 0,441 468,987 1005 5 0,5 0,915 0,451 670,047 1006 6 0,6 0,935 0,461 900,052 1007 7 0,7 0,951 0,469 1153,604 1008 8 0,8 0,967 0,477 1433,146 1009 9 0,9 0,984 0,485 1739,271 1010 10 1,0 1,000 0,493 2071,234 1011 11 1,1 1,013 0,499 2419,431 1012 12 1,2 1,025 0,505 2790,775 1013 13 1,3 1,037 0,511 3182,097 1014 14 1,4 1,048 0,517 3595,692 1015 15 1,5 1,059 0,522 4029,600 Fig. 9-17  Curva-chave calculada para o vertedouro. Exemplo 9-1 Resolva o exemplo de classificação do vertedouro usando uma calculadora on-line.   CÁLCULO ONLINE. Use EMLINHA CLASSIFICACAO OGEE, com L = 30 m, HD = 10 m, velocidade de aproximação Va = 0, altura da barragem P = 30 m, borda livre Fb = 5 m, e elevação da soleira do vertedouro E = 1000 m. O resultado da calculadora é o mesmo da Tabela 9-2. 9.4  RESSALTO HIDRÁULICO [Questões]   [Problemas]   [Referências]   •   [Topo]   [Vertedouro de soleira delgada]   [Forma da soleira do vertedouro de lâmina livre]   [Curva-chave de vertedouros]   O ressalto hidráulico é um fenômeno de fluxo em canal aberto, no qual o fluxo muda repentinamente de supercrítico para subcrítico (Fig. 9-18). A equação do ressalto hidráulico é desenvolvida para um canal horizontal, para o qual o ressalto se torna estacionário, ou seja, ocorre em um local específico no canal. Um ressalto hidráulico não estacionário pode ocorrer em um canal de declividadeinclinação finita (diferente de zero). Na prática, o ressalto hidráulico estacionário é preferível ao ressalto não estacionário ou "móvel". Fig. 9-18  Ressalto hidráulico à jusante da comporta. O ressalto hidráulico é usado nas seguintes aplicações: Dissipar energia do fluxo da água sobre barragens, represas e outras estruturas hidráulicas, para evitar danos à jusante das estruturas. Recuperar a carga hidráulica à jusante de uma calha de medição. Aumentar o peso em um avental e reduzir as pressões de elevação sob uma estrutura de alvenaria. Aerar a água para fins de purificação. 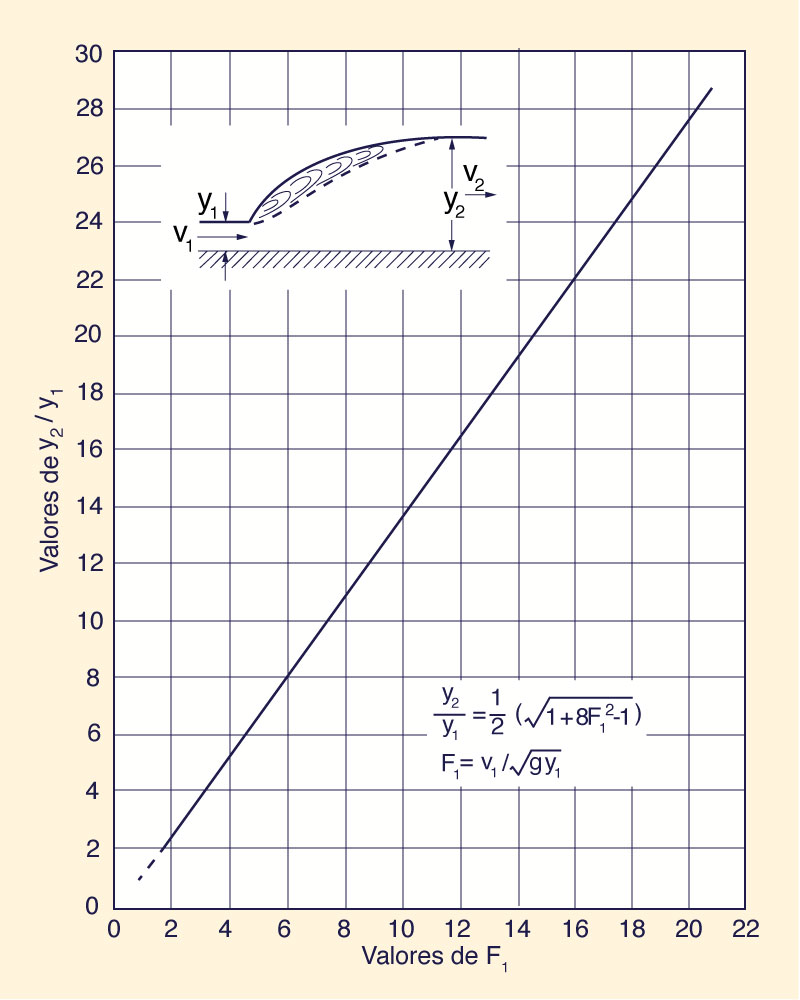Equação do ressalto hidráulico Um ressalto hidráulico será formado em um canal retangular se a seguinte equação for atendida (veja Exemplo 3-1):   y2         1                                ____  =  ____  [ (1  +  8 F1 2 )1/2  -  1 ]   y1         2                                      (9-13) Em que:   y1 = profundidade do fluxo à montante (supercrítico);                 y2 = profundidade do fluxo à jusante (subcrítico);                 F1 = número de Froude do fluxo à montante. A profundidade y1 é a profundidade inicial e y2 é a profundidade sequencial. A relação do ressalto hidráulico (Eq. 9-13) é mostrada na Fig. 9-19. Observe que para o número Froude F1 > 2, a equação é quase linear. Fig. 9-19  Relação do ressalto hidráulico. Exemplo 9-2 Dado y1 = 0,1 m e v1 = 5 m/s, calcule a profundidade sequencial y2. Confirme o resultado usando o CANAL EMLINHA 11. O número de Froude do fluxo a montante é:  F1 = 5,049. Usando a Eq. 9-13:   y2 = 0,665 m.   CÁLCULO ONLINE. Usando o CANAL EMLINHA 11, com y1 = 0,1 m e v1 = 5 m/s, o número de Froude é: F1 = 5,049. A profundidade sequencial é y2 = 0,665 m, confirmando o cálculo manual. Tipos de ressalto hidráulico Os ressaltos hidráulicos são classificados como mostrado na Tabela 9-3 (Chow, 1959). Table 9-3  Tipos de ressalto hidráulico. Número de Froude à montante F1 Tipo de ressalto Descrição gráfica 1,0 - 1,7 Ondular 1,7 - 2,5 Fraco 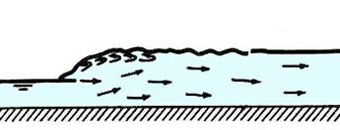2,5 - 4,5 Oscilante 4,5 - 9,0 Estável > 9,0 Forte 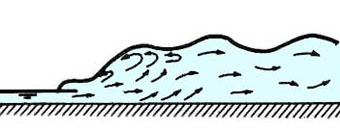Características do ressalto hidráulico A perda de energia é:                                   (y2  -  y1)3                                 ΔE  =  E1  -  E2  =  ______________                                      4 y1 y2   (9-14) [Veja também o Vídeo do laboratório:  Ressalto hidráulico]. A perda de energia relativa é:   ΔE                   E2                                 ______  =  1  -  ______    E1                   E1   (9-15) A eficiência do ressalto é:    E2           ( 1  +  8 F12 )3/2  -  4 F12  +  1                              ______  =  _______________________________    E1                     8 F12 ( 2  +  F12 ) (9-16) A altura do ressalto é:                                                                hj  =  y2  -  y1                                       (9-17) A altura relativa do ressalto é:   hj            y2          y1                    _____  =  _____  -  _____  E1           E1          E1   (9-18) Em que:   y1 /E1 = profundidade inicial relativa;                 y2 /E1 = profundidade sequencial relativa. 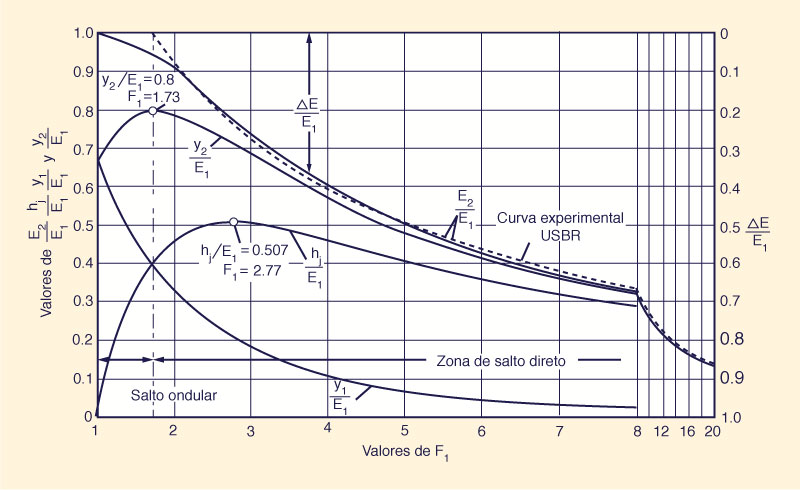Em termos do número de Froude do fluxo à montante, a altura relativa do ressalto é:    hj             ( 1  +  8 F12 )1/2  -  3                               ______  =  _______________________    E1                     2  +  F12 (9-19) A Figura 9-20 é um retrato gráfico das características do ressalto hidráulico. Observe o seguinte: A profundidade relativa sequencial atinge um valor máximo y2 /E1 = 0,8 para F1 = 1,73. A altura relativa do ressalto atinge um valor máximo hj /E1 = 0,507 para F1 = 2,77. Confirma-se que, para F1 = 1, a profundidade inicial y1 é igual a 2/3 (0,667) da energia específica E1. Para F > 3, as mudanças em todas as características tornam-se graduais. Fig. 9-20  Características do ressalto hidráulico. 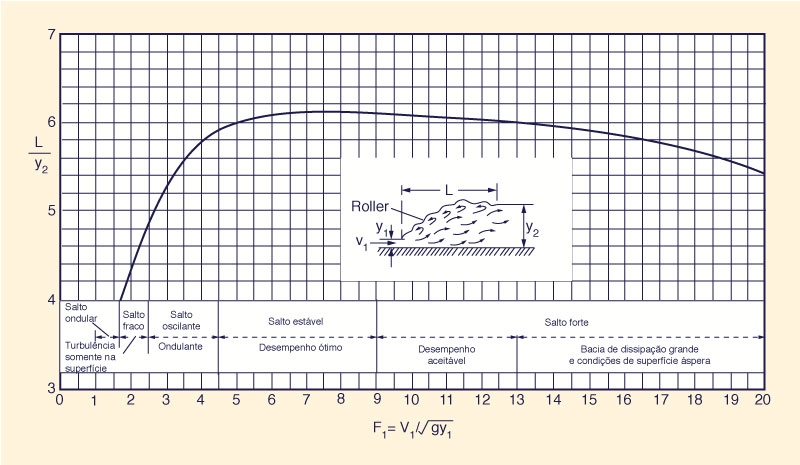Eficiência do ressalto hidráulico Com referência à Fig. 9-21, a eficiência do ressalto hidráulico é:    E2           ( 1  +  8 F12 )3/2  -  4 F12  +  1                              ______  =  _______________________________    E1                     8 F12 ( 2  +  F12 ) (9-16) Fig. 9-21  Desenho esquemático do ressalto hidráulico. F1 = v1 / (gy1)1/2 F2 = v2 / (gy2)1/2 v1y1 = v2 y2 v12y12 = v22 y22 F12 y13 = F22 y23 F22 = F12 / (y2 / y1)3 A equação do ressalto hidráulico é (Eq. 9-13): y2 / y1 = (1/2) [ (1 + 8 F12)1/2 - 1 ] N 2 = 1 + 8 F12 y2 / y1 = (1/2) [ N - 1] 2 (y2 / y1) = N - 1 (y2 / y1)3 = (1/8) [ N - 1]3 2 (y2 / y1)3 = (1/4) [ N - 1]3 N = ( 1 + 8 F12)1/2 N 3 = ( 1 + 8 F12)3/2 N 2 - 1 = 8 F12 F12 = ( N 2 - 1) / 8 4 F12 = ( N 2 - 1) / 2 A eficiência do ressalto hidráulico é: E2/E1 = [ y2 + v22/(2g) ] / [ y1 + v12/(2g) ] E2/E1 = [ y2(1 + F22/2) ] / [ y1(1 + F12/2) ] E2/E1 = 2 (y2/y1) {1 + F12 / [ 2 (y2/y1)3] } / (2 + F12) E2/E1 = (N - 1) {1 + (N 2 - 1) / [ 2 (N - 1)3 ] } / (2 + F12) E2/E1 = (N 2 - 1)(N - 1) {1 + (N 2 - 1) / [ 2 (N - 1)3 ] } / [8 F12(2 + F12) ] E2/E1 = [ (N 2 - 1)(N - 1) + (1/2)(N + 1)2 ] / [ 8 F12(2 + F12) ] E2/E1 = { (N 3 - N 2 - N - 1) + [ (N 2/2) + N + (1/2)] } / [ 8 F12(2 + F12) ] E2/E1 = { (N 3 - [(N 2 - 1)/2] + 1} / [ 8 F12 (2 + F12) ] E2/E1 = [ (1 + 8 F12)3/2 - 4F12 + 1] / [ 8 F12(2 + F12) ]   RESPOSTA. Exemplo 9-3 Dado q = 0,5 m2/s e ΔE = 0,678 m, calcular as profundidades sequentes y1 e y2. Confirme o resultado usando o CANAL EMLINHA 16. O cálculo prossegue por tentativa e erro. Suponha um valor baixo de F1, digamos que seja 2. Use a Eq. 9-13 para calcular y2 / y1. Use a Eq. 9-14 para resolver y1. Resolva para a velocidade à montante:  v1 = q / y1 Calcule o valor de F1. Se o valor calculado na Etapa 5 for o mesmo que o assumido na Etapa 1 (dentro de uma certa tolerância), pare e relate as profundidades sequenciais. Caso contrário, aumente o valor de F1, por um incremento adequado, e voltar ao Passo 1.   CÁLCULO ONLINE. Use CANAL EMLINHA 16, com q = 0,5 m2/s e ΔE = 0,678 m. As profundidades sequenciais são:   y1 = 0,1 m e y2 = 0,665 m. Exemplo 9-4 Dado y1 = 0.1 m e v1 = 5 m/s, calcule a eficiência do resalto hidráulico. Confirme o resultado usando o CANAL EMLINHA 18. O número de Froude do fluxo à montante é:  F1 = 5,049. Usando a Eq. 9-16:  E2 / E1 = 0,505.   CÁLCULO ONLINE. Usando CANAL EMLINHA 18, com y1 = 0,1 m, e v1 = 5 m/s, o número de Froude é: F1 = 5,049. A eficiência do ressalto é: E2 / E1 = 0,505, confirmando o cálculo manual. 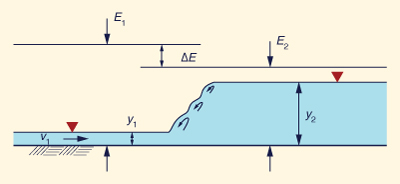Comprimento do ressalto hidráulico O comprimento do ressalto hidráulico é definido como a distância medida da face frontal até um ponto (na superfície da água) localizado imediatamente à jusante do rolo (consulte a Fig. 9-21). O comprimento relativo do ressalto L/y2 foi determinada experimentalmente. Varia de cerca de 5,0 a 6,15 para uma ampla gama de números Froude à montante. Dentro da faixa de 4.5 ≤ F1 ≤ 13, o comprimento relativo do ressalto é um pouco maior que 6 (Fig. 9-22). Fig. 9-22  Comprimento do ressalto hidráulico (U.S. Bureau of Reclamation). 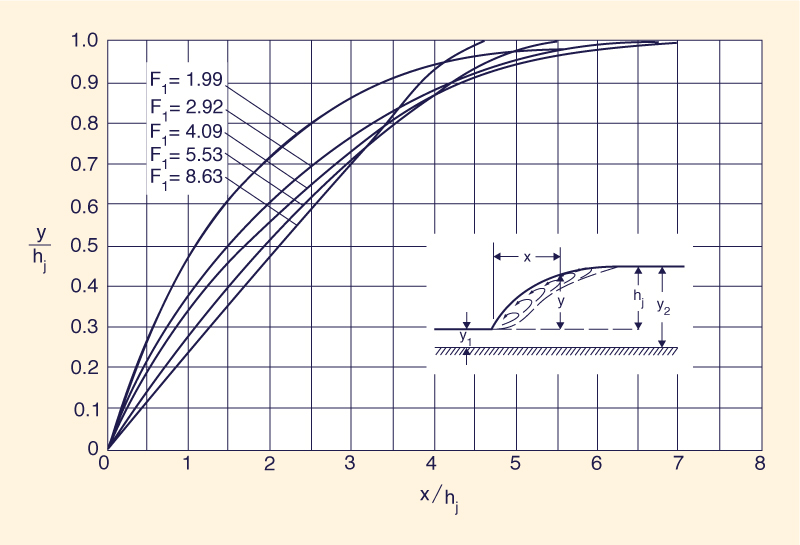Perfil do ressalto hidráulico Medições experimentais mostraram que o perfil real da superfície do ressalto hidráulico varia um pouco com o número de Froude à montante. Os perfis podem ser plotados como curvas sem dimensão, como mostrado na Fig. 9-23. Uma imagem mais próxima de um ressalto hidráulico é mostrado na Fig. 9-24. Fig. 9-23  Perfis adimensionais do ressalto hidráulico (Chow, 1959). Fig. 9-24  Ressalto hidráulico. QUESTÕES [Problemas]   [Referências]   •   [Topo]   [Vertedouro de soleira delgada]   [Forma da soleira do vertedouro de lâmina livre]   [Curva-chave de vertedouros]   [Ressalto hidráulico]   Como o fluxo variado rapidamente difere do fluxo variado gradualmente? Existe uma solução teórica de fluxo unidimensional de variação rápida? Qual é o expoente da classificação em um vertedouro de soleira espessa? Qual é o coeficiente da curva-chave dos vertedouros altos em unidades habituais nos EUA? O que significa "ogee"? Qual é a justificativa para o uso de um vertedouro do tipo labirinto? Qual é o risco quando o fluxo sobre um vertedouro excede o estágio de projeto? Que condição de fluxo produz um ressalto hidráulico? A equação do ressalto hidráulico é linear ou não linear? Como é medido o comprimento do ressalto hidráulico? PROBLEMAS [Referências]   •   [Topo]   [Vertedouro de soleira delgada]   [Forma da soleira do vertedouro de lâmina livre]   [Curva-chave de vertedouros]   [Ressalto hidráulico]   [Questões]   Um vertedouro de emergência está sendo considerado para a Demerera Water Conservancy para proteger a integridade da barragem sob condições de mudanças climáticas (semelhante à Fig. 9-25). Suponha que as comportas existentes seriam inoperantes durante uma grande inundação devido à elevada cota na jusante (cauda). Determine o comprimento do vertedouro de transbordamento livre necessário para passar na provável inundação máxima (PMF). Os seguintes dados são aplicáveis: PMF duração de 1 dia: 428 mm Captação hidrológica: 18 mm Área de drenagem contribuinte: 582 km 2 Base de tempo do hidrograma de inundação: 3 dias Elevação da soleira do aterro: 18.288 m Altitude da soleira do vertedouro: 17.526 m Borda livre: 0,3 m Coeficiente de descarga do vertedouro: 1,45 Para simplificar, assuma um hidrograma de inundação de forma triangular. Use a borda livre para conter o PMF. Fig. 9-25  O vertedouro de 8000 pés da área de conservação de Boerasirie. Projete uma seção do vertedouro com uma face vertical à montante e um comprimento de soleira L = 150 pés. A vazão do projeto é Q = 50.000 pés3/s. A superfície da água à montante na vazão do projeto está em Elev. 750 pés, e o piso médio do canal está em Elev. 650 pés (veja a Fig. 9-6 para exemplo gráfico). Use CANAL EMLINHA CLASSIFICACAO OGEE para determinar a curva-chave de um vertedouro do tipo ogee com comprimento L = 15 m, carga de pojeto Hd = 2 m, elevação da soleira do vertedouro = 1045 m, elevação do leito do rio = 1000 m, e borda livre Fb = 1 m. Desconsidere a velocidade de aproximação. Qual deve ser o comprimento do vertedouro para passar no provável máximo de inundação (PMF) QPMF = 250 m3/s enquanto ocupando toda a borda livre? Expresse o comprimento do vertedouro até 0,1 m mais próximo em excesso. Prove a Eq. 9-14. Prove a Eq. 9-19. Calcule a perda de energia em um ressalto hidráulico, considerando as profundidades sequenciais y1 = 0,58 m e y2 = 2,688 m. Calcule a altura relativa do ressalto hidráulico hj /E1 para F1 = 3. Use CANAL EMLINHA 11 para calcular a profundidade sequencial y2 através de um ressalto hidráulico quandoa vazão for q = 5 m2/s e a profundidade inicial for de y1 = 0,58 m. Use o CANAL EMLINHA 12 para determinar a profundidade sequencial y2 e a perda de energia ΔE através de um ressalto hidráulico quando a vazão for q = 10 pés2/s e a profundidade do fluxo a montante for y1 = 0,5 pés. Use CANAL EMLINHA 16 para calcular a profundidades sequencial através de um ressalto hidráulico quando a vazão for q = 10 pés2 e a perda de energia ΔE = 3,287 pés. Use CANAL EMLINHA 16 para calcular a profundidades sequencial através de um ressalto hidráulico quando a vazão for q = 5 m2 e a perda de energia ΔE = 1,5 m. Use CANAL EMLINHA 18 para calcular a eficiência do ressalto hidráulico E2/E1 para q = 10 pés2/s e y1 = 0,5 pés. REFERÊNCIAS •   [Topo]   [Vertedouro de soleira delgada]   [Forma da soleira do vertedouro de lâmina livre]   [Curva-chave de vertedouros]   [Ressalto hidráulico]   [Questões]   [Problemas]   Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, New York. Roberson, J. A., J. J. Cassidy, e M. H. Chaudhry. 1998. Hydraulic Engineering. John Wiley e Sons, New York, Second edition. Pugh, C. A., e E. W. Gray. 1984. Fuse Plug Embankments in Auxiliary Spillways - Developing Design Guidelines e Parameters, United States Committee on Large Dams (as cited in U.S. Bureau of Reclamation). http://ponce.sdsu.edu/canais/index.html 200626 08:00