[Canales No Erosionables]   [Canales Erosionables]   [Fuerza Cortante]   [Fuerza Cortante Permisible]   [Obras de Arte]   [Preguntas]   [Problemas]   [Bibliografía]   •   CAPÍTULO 6:  DISEÑO DE CANALES 6.1  CANALES NO EROSIONABLES [Canales Erosionables]   [Fuerza Cortante]   [Fuerza Cortante Permisible]   [Obras de Arte]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   Existen dos tipos de canales: (1) no erosionables, y (2) erosionables. Los canales no erosionables son aquéllos revestidos con un material de construcción durable, como el concreto o la mampostería de piedra. Los canales erosionables se excavan en la superficie del terreno y, por lo tanto, están en contacto directo con el suelo subyacente. El diseño de los canales erosionables es mucho más complejo que el de canales no erosionables. El diseño de canales no erosionables comienza con la selección de una fórmula de flujo uniforme (Capítulo 5). Se consideran los siguientes factores: La rugosidad de la superficie La rugosidad de la superficie, o fricción a lo largo del perímetro mojado, depende del tipo y acabado del material de revestimiento del canal. Por lo general, las superficies más gruesas producen una fricción más alta que las superficies más lisas (Fig. 6-1). Fig. 6-1  Un canal con revestimiento de albañilería. Velocidad mínima permisible Todos los canales llevan una cierta cantidad de sedimentos (arena, limo y arcilla). Por consecuencia, el flujo en canales con pendiente de fondo muy pequeña puede llevar a la deposición del sedimento. Por lo tanto, para evitar obstrucciones, se requiere de una velocidad mínima permisible, es decir, una pendiente de fondo mínima. Pendiente de fondo máxima Todos los canales no erosionables tienen una tendencia a desarrollar ondas de rollo si el número de Verdenikov V > 1 (Capítulo 1). Para evitar las ondas de rollo, la pendiente de fondo debe mantenerse por debajo de un valor máximo, el cual es función de la hidráulica del flujo. La Figura 6-2 muestra una serie de caídas construidas en un canal con el fin de reducir la pendiente de fondo. Fig. 6-2  Serie de caídas construidas para disminuir la pendiente de fondo, Canal La Joya, Arequipa, Perú. Forma de la sección transversal La sección de conducción máxima, y por lo tanto, descarga máxima, es aquélla que tiene el perímetro mojado mínimo para una área de flujo dada. Esta forma de sección transversal se conoce como la sección hidráulica óptima. 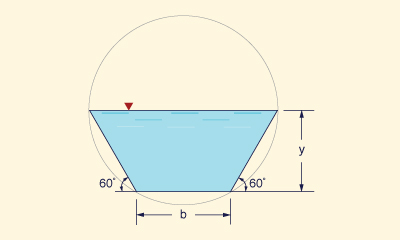La sección hidráulica circular óptima es un semicírculo. La sección hidráulica trapezoidal óptima es la mitad de un hexágono regular inscrito en un círculo (Chow, 1959) (Fig. 6-3). Sin embargo, en la práctica, otras consideraciones de diseño son usualmente más importantes que la conducción máxima. Fig. 6-3  La mejor sección hidráulica trapezoidal. Pendientes laterales El talud es z H: 1 V, en el cual z = 0 para una sección rectangular y z > 0 para una sección trapezoidal. El valor del talud es una decisión de diseño que varía con las condiciones locales (Fig. 6-4). Los taludes típicos varían en el rango 0 ≤ z ≤ 3. Fig. 6-4  Transición de un canal de forma rectangular a trapezoidal. Bordo libre El bordo libre es la profundidad vertical medida por encima de la profundidad de diseño, hasta la profundidad total del canal (Fig. 6-5). Su propósito es proveer un factor de seguridad y minimizar la posibilidad de desbordamiento de ondas. Fig. 6-5  Bordo libre en el Canal San Luis, California. Reducción de riesgo de deslizamientos En canales construidos sobre taludes naturales, se debe reducir el riesgo de deslizamientos, los cuales según su severidad pueden dañar el canal hasta hacerlo inoperable. Algunas laderas son propensas a deslizamientos, pero otras no lo son. Es necesario hacer estudios geológicos/geotécnicos para reducir el riesgo de deslizamiento. La Figura 6-6 muestra una ruptura ocasionada por un deslizamiento (Ver video relacionado). Fig. 6-6  Rotura ocasionada por el deslizamiento del 4 de Noviembre del 2010 en el Canal La Cano, Arequipa, Perú. Revestimiento de canales Los canales pueden ser revestidos con diversos materiales, incluyendo concreto, mampostería, acero, hierro fundido, madera, vidrio y plástico. El revestimiento de los canales reduce la fricción y los costos de mantenimiento. La Figura 6-7 muestra el Río Santa Ana, en Huntington Beach, California, el cual ha sido pavimentado con concreto para reducir el tirante o profundidad de agua y poder controlar las inundaciones. Fig. 6-7  Ejemplo de río pavimentado:  Río Santa Ana, Huntington Beach, California. La Figura 6-8 muestra el Arroyo Alamar, el cual fue recientemente revestido con concreto (2013). Cabe mencionar que las prácticas actuales de diseño ambiental generalmente no recomiendan el revestimiento de canales naturales con concreto. Fig. 6-8  El Arroyo Alamar, en Tijuana, Baja California, México. Velocidad mínima permisible Todo flujo acarrea cierta cantidad de sólidos suspendidos, en forma de sedimentos. Los valores típicos de carga suspendida son de 200 a 300 partes por millón (o ppm, equivalentes en este rango a mg/L) (Ponce, 2014). La condición de no resbalamiento en el perímetro del canal (es decir, la velocidad local del flujo es nula) produce un esfuerzo cortante, el cual resulta en el arrastre de sedimentos. Una vez incorporado el sedimento, debe ser transportado; de lo contrario, se depositará y eventualmente obstruirá el canal. La velocidad mínima para evitar la sedimentación/obstrucción es la velocidad mínima permisible. El cálculo de la velocidad mínima permisible puede hacerse utilizando el diagrama de Shields, el cual relaciona el esfuerzo cortante adimensional τ* con el número de Reynolds del perímetro R*, como se muestra en la Fig. 6-9. La curva sólida separa el movimiento (por encima de la curva) de la ausencia de movimiento (por debajo de la curva). Fig. 6-9  Diagrama de Shields para el inicio del movimiento (Sociedad Americana de Ingenieros Civiles, 1975). Número de Froude mínimo y velocidad mínima permisible La ley de la fricción cuadrática, con el esfuerzo de corte en el fondo τo, se expresa de la siguiente manera:   τo  =  ρ f V 2   (6-1) El criterio de Shields para la iniciación del movimiento es:                  τo τ* = _____________  ≥  τ*c           (γs - γ ) ds (6-2) en el cual τ* = esfuerzo de corte adimensional, γs = peso específico de las partículas, γ = peso específico del agua, ds = diámetro de la partícula del sedimento, y τ*c = esfuerzo de corte crítico adimensional. La Figura 6-9 muestra la curva de Shields, es decir, la variación del esfuerzo de corte crítico adimensional τ*c con el número de Reynolds del perímetro R*:             U* ds R* = _________               ν (6-3) en el cual U* = velocidad de corte = (τo /ρ)1/2 = ( f )1/2 V, y ν = viscosidad cinemática. El número de Froude F es:               V F = ___________          (g D )1/2 (6-4) en el cual V = velocidad media, D = profundidad hidráulica, y g = aceleración de la gravedad. Sustituyendo las Ecs. 6-1 y 6-4 en la Ec. 6-2:              f D F 2 _____________________  ≥  τ*c     [ (γs / γ ) - 1 ] ds (6-5) En la mayoría de los casos la relación de pesos específicos de sedimento y agua γs /γ es 2.65. Por lo tanto, en términos del número de Froude, el criterio de Shields para el inicio de movimiento se reduce a:              1.65 τ*c (ds / D ) F  ≥  [ __________________ ] 1/2                          f (6-6) Para aplicaciones prácticas, se puede considerar un valor constante del esfuerzo de corte crítico adimensional τ*c = 0.04. La Figura 6-9, muestra que este valor se encuentra en el rango:  4 ≤ R* ≤ 60. Por lo tanto:              0.066 (ds / D ) F  ≥  [ ________________ ] 1/2                        f (6-7) La Ecuación 6-7 es el criterio práctico de Froude basado en el inicio del movimiento de Shields, aplicable a un amplio rango de números de Reynolds del perímetro. Como un ejemplo práctico del uso de la Ec. 6-7, asuma ds = 0.4 mm, D = 1 m, y un valor medio del factor de fricción de Chezy adimensional f = 0.0035 (equivalente a un factor de fricción de Darcy-Weisbach f = 0.028). De acuerdo a la Ec. 6-7:               F  ≥  0.087                         (6-8) Combinando las Ecs. 6-4 y 6-7:              0.066 (g ds) V  ≥  [ ______________ ] 1/2                       f (6-9) De acuerdo a la Ec. 6-9, la velocidad mínima permisible para esta condición de flujo es: Vmin = 0.27 m/s. Es posible obtener un valor más preciso del número de Froude mínimo y de la velocidad mínima permisible utilizando el valor real del esfuerzo cortante crítico adimensional calculado con la Ec. 6-7. El valor más preciso se utiliza en vez de la aproximación τ*c = 0.04. El siguiente algoritmo de iteración explica el procedimiento: Asumir R* Usando la Fig. 6-9, encontrar τ* = τ*c Con τ*, use la Ec. 6-2 para calcular τo Usando la Ec. 6-1, calcular la velocidad de corte U* = (τo /ρ)1/2 Usando la Ec. 6-3, calcular el nuevo valor de R* Parar si el nuevo valor de R* es el mismo que el asumido en el Paso 1 (dentro de una cierta tolerancia), y usar el último valor de τ*c (calculado en el Paso 2) en la Ec. 6-6; De otra manera, regresar al Paso 1 usando el nuevo valor de R*, y repetir la iteración.  Ejemplo 6-1. Asumir los siguientes datos: diámetro de la partícula ds = 0.4 mm, profundidad hidráulica D = 1 m, factor de fricción de Darcy-Weisbach adimensional f = 0.0035, y temperatura del agua T = 20°C. Usando el criterio de Shields para el inicio de movimiento, calcular el número de Froude mínimo y la velocidad mínima permisible.   CÁLCULO EN LÍNEA. Usando VELOCIDAD DE SHIELDS EN LÍNEA, el número de Froude mínimo es Fmin = 0.081, y la velocidad mínima permisible es Vmin = 0.25 m/s. Nótese que estos resultados son ligeramente diferentes a los obtenidos usando las Ecs. 6-7 y 6-9. Pendiente del canal La pendiente de diseño de un canal se rige generalmente por la alineación seleccionada y la topografía del terreno. En general, la pendiente escogida depende del propósito o uso del canal. Por ejemplo, los canales utilizados para riego y energía hidroeléctrica requieren de pendientes pequeñas, a fin de no perder mucha carga durante la conducción. Los taludes dependen de las condiciones del suelo y del proceso constructivo; por lo general el talud escogido es lo más pronunciado posible. El Bureau of Reclamation de los EE.UU recomienda como estándar un talud de 1.5 H: 1 V para canales revestidos. La posibilidad de que se desarrollen ondas de rollo aumenta en canales revestidos con pendientes pronunciadas, cuando el número de Vedernikov V  > 1 (Capítulo 1). Bordo libre El bordo libre es la distancia vertical desde la parte superior del canal a la superficie del agua para el flujo de diseño. Esta distancia debe ser lo suficientemente grande para evitar que las olas o las fluctuaciones en la superficie del agua causen desbordes. Esta característica es de suma importancia en el diseño de canaletas elevadas, ya que la estructura de soporte de la canaleta puede ser puesta en peligro por un desbordamiento (Fig. 6-10). Fig. 6-10  Desbordamiento después de lluvias fuertes:  Conducto Dulzura, Condado de San Diego, California, el 5 de Marzo de 2005. No hay una regla universalmente aceptada para la determinación del bordo libre. La acción del viento y la marea pueden inducir olas altas, por lo que es necesario asegurar que estas olas se mantengan dentro de los límites del canal. En la práctica, el diseño de los bordos libres varía entre menos del 5% a más del 30% de la profundidad del flujo de diseño. La experiencia indica que para canaletas lisas, semicirculares, con alineación en tangente, con velocidades de flujo menores a la crítica, y con un máximo de 2.4 m/s, el bordo libre de 6% del diámetro de la canaleta es adecuado. Para canaletas en curva, se debe aumentar el bordo libre para evitar desbordamiento (Chow, 1959). Los criterios de diseño permiten el uso de la totalidad o parte del bordo libre en el caso de una inundación máxima probable (Ponce, 2014). De acuerdo con el Bureau of Reclamation de los EE.UU., los valores de bordo libre se encuentran entre 1 pie (0.3 m) para canales laterales pequeños, y 4 pies (1.2 m) para canales con flujos de 3 000 pies cúbicos por segundo (85 m3/s) o mayores. Se puede utilizar la siguiente fórmula: Fb  =  ( C y ) 1/2 (6-10) en la cual Fb = bordo libre, en pies; y = profundidad del agua, en pies; y C = coeficiente, el cual varía de C = 1.5 para una capacidad de 20 pies cúbicos por segundo (0.57 m3/s) a C = 2.5 para una capacidad de 3,000 pies cúbicos por segundo (85 m3/s) o mayor. La Figura 6-11 muestra la altura de revestimiento y la altura del banco, aplicable en el diseño del bordo libre. Fig. 6-11  Altura de revestimiento y altura del banco recomendadas por el U.S. Bureau of Reclamation (Chow, 1959). 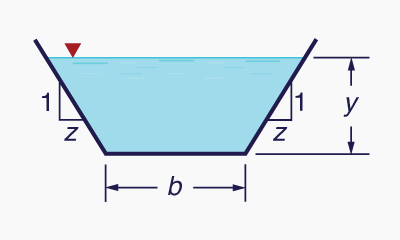Dimensiones de la sección transversal Las dimensiones de la sección transversal de un canal se determinan por medio de los siguientes pasos: Seleccionar la descarga de diseño Q Seleccionar el ancho de fondo b Seleccionar el talud z  [z H : 1 V] (Fig. 6-12) Fig. 6-12  Diagrama del ancho de fondo b y talud z. Seleccionar la pendiente de fondo S Estimar el valor del n de Manning (Capítulo 5:  n de Manning) Usando Q, b, z, S, y n [Pasos 1 a 5], calcular la profundidad normal yn, la velocidad normal vn, y el número de Froude normal Fn ( Capítulo 5:  Cálculo) Comprobar si la velocidad normal vn y el número de Froude normal Fn son lo suficientemente grandes para evitar la obstrucción con sedimentos (ver Velocidad mínima permisible en este Capítulo) Seleccionar un bordo libre adecuado Fb . La Figura 6-13 muestra recomendaciones de ancho de fondo y profundidad de flujo en canales revestidos. Fig. 6-13  Ancho de fondo y profundidad de flujo recomendados por el Bureau of Reclamation de los EE.UU. para canales revestidos (Chow, 1959).  Ejemplo 6-2. Diseñar un canal para las siguientes condiciones: Q = 10 m3/s; b = 5 m; z = 2; S = 0.0016; n = 0.025. Iterando con la Ec. 5-55, la profundidad normal es yn = 1.049 m y la velocidad normal es vn = 1.342 m/s. El número de Froude basado en la profundidad normal es Fn = 0.418. El número de Froude calculado es mucho mayor que 0.087 (Ec. 6-8), el valor mínimo requerido para evitar la sedimentación. Se asume un bordo libre de Fb = 0.6 m.   CÁLCULO EN LÍNEA. Usando la calculadora CANAL EN LÍNEA 01, la profundidad normal es yn = 1.049 m; la velocidad normal es vn = 1.342 m/s; el número de Froude (basado en la profundidad hidráulica D = 0.81 m) es: Fn = 0.476. Nótese que el número de Froude real es aquél basado en la profundidad hidráulica (Ec. 4-6). Para un canal hidráulicamente ancho, en el cual D ≅ R, ambos números de Froude resultan aproximadamente iguales. La Figura 6-14 muestra un canal construido en 1993 en Ceará, Brasil, con el propósito de conducir agua para combatir una sequía regional. Las características hidráulicas son: Q = 8.32 m3/s, b = 5 m, z = 1.5, S = 0.00005, y n = 0.015. Usando la calculadora CANAL EN LÍNEA 01, los resultados son:   profundidad normal yn = 1.915 m, velocidad normal vn = 0.552 m/s, y número de Froude Fn = 0.149. Cogerh Fig. 6-14  Canal del Trabajador (Canal do Trabalhador), Ceará, Brasil (1993). 6.2  CANALES EROSIONABLES [Fuerza Cortante]   [Fuerza Cortante Permisible]   [Obras de Arte]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Canales No Erosionables]   El diseño de un canal erosionable es mucho más complejo que el de un canal no erosionable. La estabilidad a largo plazo del perímetro del canal depende de las propiedades del material de revestimiento (arena, limo, arcilla o mezclas), y de las propiedades del sedimento transportado. Los cambios en el flujo de agua y sedimentos producen variaciones en la sección transversal, ya sea en la profundidad del canal, en el ancho del canal, o en ambos. La estabilidad del perímetro se evalúa en función de dos criterios: La velocidad máxima permisible, y El esfuerzo cortante máximo permisible. Dada la Ec. 6-1, estos dos métodos se relacionan de la siguiente manera: τo max  =  ρ f (Vmax )2 (6-11)  Ejemplo 6-3. Calcular la velocidad máxima permisible correspondiente a un esfuerzo cortante máximo permisible de 20 N/m2. Asumir f = 0.0035, es decir, Darcy-Weisbach f = 0.028. Usando la Ec. 6-11: Vmax = [τo max / (ρ f ) ] 1/2 = [ 20 N/m2 / (1000 N s2/m4 × 0.0035 ) ] 1/2 = 2.39 m/s.  Ejemplo 6-4. Calcular la velocidad máxima permisible correspondiente a un esfuerzo cortante máximo permisible de 0.1 lb/ft2. Asumir f = 0.005, es decir, Darcy-Weisbach f = 0.04. Usando la Ec. 6-11: Vmax = [τo max / (ρ f ) ] 1/2 = [ 0.1 lb/pie2 / (1.94 lbs-s2/ft4 × 0.005 ) ] 1/2 = 3.21 pies/s. Canales con vegetación La Tabla 6-1 muestra los valores típicos del esfuerzo cortante máximo permisible para diversos tipos de revestimiento en canales con vegetación. Tabla 6-1   Valores típicos del esfuerzo cortante máximo permisible. 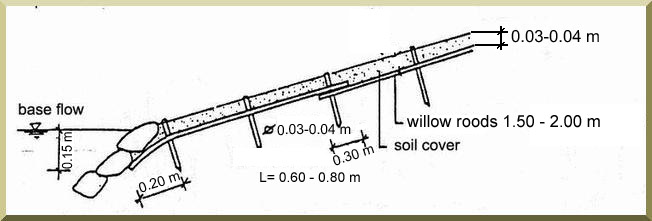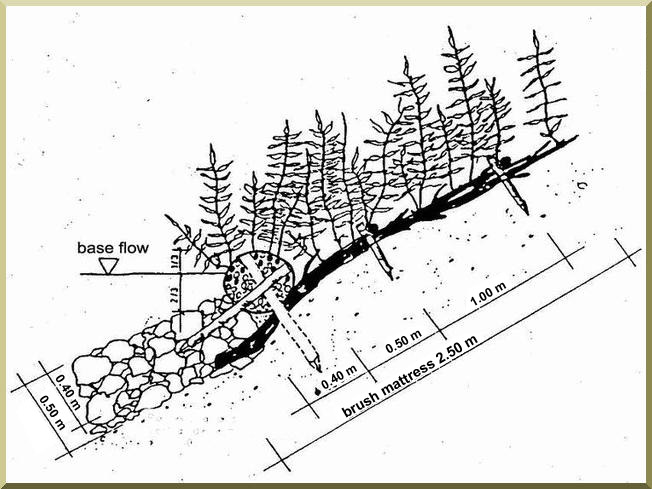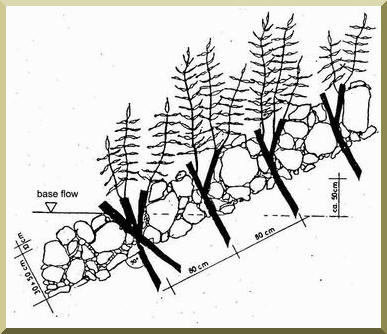Tipo de revestimiento Esfuerzo cortante máximo permisible (N/m2) Césped (establecido recientemente) 20-30 Césped (establecido hace años) 15-18 Rollos de vegetación cubiertos con lodo 60-70 Rollos de vegetación seca 100-150 Rollos de vegetación seca, con peso 60-100 Colchón de arbustos 150-300 Estacado en enrocado > 140 Alder / Aliso 80-140 Gaviones 80-140 La Figura 6-15 muestra detalles del diseño de un revestimiento de canal usando un colchón de arbustos. Fig. 6-15 (a)  Diseño de un colchón de arbustos:  Vista en planta. Fig. 6-15 (b)  Diseño de un colchón de arbustos:  Vista lateral. Fig. 6-15 (c) Diseño de un colchón de arbustos:  Vista lateral después de varios meses. Fig. 6-15 (d) Diseño de colchón de arbustos:  Vista después de terminadoo el proyecto. La Figura 6-16 muestra los detalles de un revestimiento de canal utilizando estacado en enrocado. Fig. 6-16 (a)  Ilustración de un estacado en enrocado Fig. 6-16 (b)  Estacado en enrocado:  Poco tiempo después de la instalación. Fig 6-16 (c)  Estacado en enrocado:  Algún iempo después de su instalación. Fig. 6-16 (d)  Estacado en enrocado:  De 2 a 5 años después de su instalación. Fig. 6-16 (e)  Estacado en enrocado:  Vista después de varios años. Canales revestidos con gaviones Un sistema de gaviones consiste en cestas fabricadas con malla de alambre, llenas de grava, las cuales se anclan sobre los taludes (Fig. 6-17). Las piedras pequeñas se colocan dentro de la malla, lo cual permite una misma resistencia al desplazamiento. Ésta es una ventaja en la construcción de revestimiento de roca en zonas con acceso difícil. Las cestas de alambre también permiten el revestimiento de canales con taludes más pronunciados (hasta verticales). Los gaviones se pueden construir con alambre comercialmente disponible o con malla ciclónica. Fig. 6-17  Colocación de colchones de gaviones. Los gaviones son una manera eficaz de controlar la erosión en arroyos, ríos y canales. Generalmente se diseñan para resistir velocidades de flujo altas [5 m/s o mayores]. 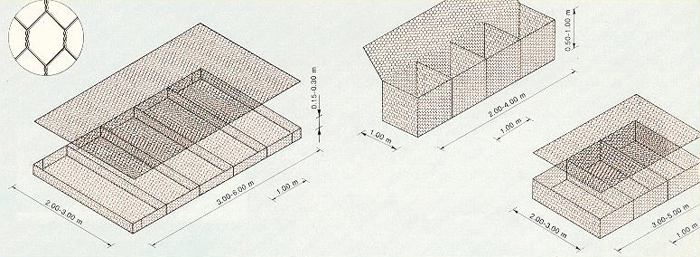Las unidades de gaviones tienen longitudes desde 2 m hasta cerca de 30 m. Por lo tanto, pueden ser utilizadas tanto en pequeñas zanjas como en canales grandes (Fig. 6-18). Fig. 6-18  Dimensiones de los colchones de gaviones. Los canales revestidos con gaviones son una solución intermedia entre la escollera y el concreto. Cuando se usa el mismo tamaño de rocas en los gaviones y la escollera, la velocidad permisible en los gaviones es de tres a cuatro veces mayor que la de la escollera. Una ventaja de los gaviones, en comparación con los canales revestidos de concreto, es que los gaviones pueden ser cubiertos con vegetación y, por lo tanto, confundirse hasta cierto punto con el paisaje natural (Fig. 6-19). Los canales de gaviones con vegetación tienen las siguientes ventajas: Permiten la infiltración y exfiltración Permiten el filtrado de contaminantes Mayor flexibilidad que los canales pavimentados Mayor disipación de energía que los canales de concreto Mejoran el hábitat para la flora y la fauna Son más estéticos a la vista Tienen menos costo de instalación, aunque requieren de cierto mantenimiento. Los valores de n de Manning para canales revestidos con gaviones generalmente se encuentran en el rango 0.025 ≤ n ≤ 0.030. Fig. 6-19  Revstimiento del Río Atoyac, en Oaxaca, México, con gaviones. 6.3  FUERZA CORTANTE [Fuerza Cortante Permisible]   [Obras de Arte]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Canales No Erosionables]   [Canales Erosionables]   La fuerza de cortante es la suma de los esfuerzos de tracción sobre el perímetro del canal, aplicada a un área. 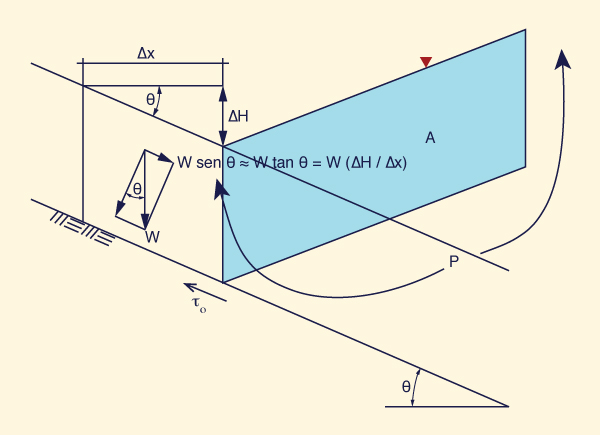Para desarrollar la ecuación del esfuerzo cortante, se asumen condiciones de equilibrio entre la fuerza de gravedad y la fuerza de fricción. La fuerza de gravedad es (Fig. 6-20): W sen θ  ≅  W tan θ  =  W (ΔH /Δx ) (6-12) en la cual W = peso del volumen de control, de área A y longitud Δx, ΔH = caída o pérdida de carga, y θ = pendiente de fondo. Fig. 6-20  Ilustración de la fuerza de gravedad. Debido a que S = ΔH /Δx, se deduce que la fuerza de gravedad actuante es: Fg  =  γ A Δx S (6-13) La fuerza de fricción resistente es: Ff  =  τo P Δx (6-14) en la cual τo = esfuerzo cortante en el fondo, y P = perímetro mojado. Igualando las fuerzas de gravedad y de fricción: τo  =  γ R S (6-15) en donde R = A /P = radio hidráulico. 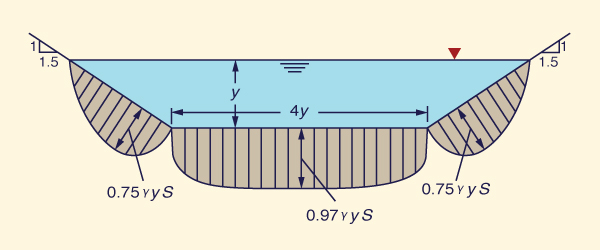Para los canales hidráulicamente anchos, en los cuales R ≅ D ≅ y, τo  =  γ y S (6-16) El esfuerzo cortante varía a lo largo del perímetro mojado, alcanzando un valor máximo a lo largo del centro del canal. La Figura 6-21 muestra una variación típica para una sección transversal trapezoidal, en la cual b/y = 4 y z = 1.5. Fig. 6-21  Variación de la fuerza cortante en un canal trapezoidal, con b/y = 4 y z = 1.5 (Chow, 1959). 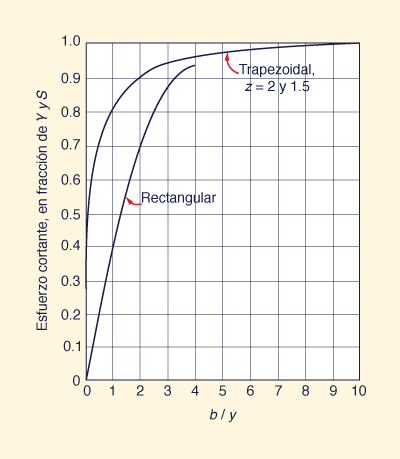En la línea central del fondo, el esfuerzo cortante se acerca asintóticamente a su valor máximo: τb = γyS , como se muestra en la Fig. 6-22. 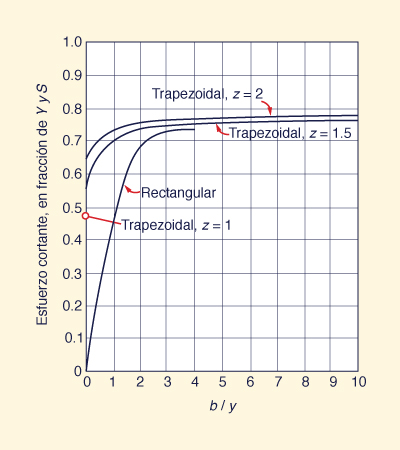En los taludes del canal, la tensión de tracción se acerca asintóticamente a una fracción del valor total: τs = 0.78 γyS , como se muestra en la Fig. 6-23. Fig. 6-22  Variación del esfuerzo cortante máximo en el fondo del canal en función de la relación de aspecto b/y (Chow, 1959). Fig. 6-23 Variación del esfuerzo cortante máximo en los taludes en función de la relación de aspecto b/y (Chow, 1959). Relación de fuerza cortante La Figura 6-24 muestra tres partículas sobre el perímetro del canal, una en el lado izquierdo, otra en el lado derecho, y la tercera a nivel del suelo (fondo). La relación de fuerza cortante K se define como sigue:            a τs            τs K  =  _______  =  ______            a τL            τL (6-17) . en la cual a = área efectiva de la partícula, τs = esfuerzo cortante en el talud, y τL = esfuerzo cortante en el fondo. 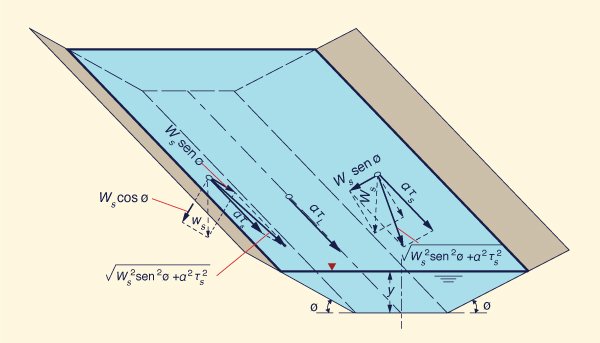Fig. 6-24 Ilustración de las fuerzas que actúan sobre una partícula en reposo en el lecho de un canal (Chow, 1959). El valor de K es una función de la pendiente lateral de canal φ y del ángulo de reposo θ del material de revestimiento. Para derivar K, se consideran las dos fuerzas que actúan sobre una partícula de peso sumergido Ws apoyada sobre el talud, con tensión de tracción τs (Fig. 6-20): La fuerza de tracción:  aτs El componente de la fuerza de gravedad a lo largo del talud:  Ws sen φ La fuerza resultante que actúa en el plano del talud es: Fa  =  (Ws2 sen2φ  +  a2τs2)1/2 (6-18) En el equilibrio, la fuerza de resistencia es igual a la fuerza actuante. De acuerdo a la mecánica de sólidos, la fuerza de resistencia es igual a la fuerza normal (Ws cosφ ) por el coeficiente de fricción (tanθ ): Fr  =  Ws  cosφ  tanθ (6-19) Por lo tanto: Ws  cosφ  tanθ  =  (Ws2 sen2φ  +  a2τs2)1/2 (6-20) Elevando ambos lados al cuadrado: Ws2 cos2φ  tan2θ  =  Ws2 sen2φ  +  a2τs2 (6-21) a2τs2  =  Ws2 cos2φ  tan2θ  -  Ws2 sen2φ (6-22) τs2  =  (Ws /a)2 cos2φ  tan2θ  -  (Ws /a)2 sen2φ (6-23)                                                            tan2φ τs2  =  (Ws /a)2 cos2φ  tan2θ  [ 1  -  _________ ]                                                            tan2θ (6-24)                                                      tan2φ τs  =  (Ws /a) cosφ  tanθ  [ 1  -  _________ ] 1/2                                                      tan2θ (6-25) La Ecuación 6-25 es el esfuerzo cortante en el talud de un canal de ángulo de inclinación lateral φ y ángulo de reposo (del material) θ. Para una superficie plana, con φ = 0, resulta: senφ = 0 y cosφ = 1. Por lo tanto, el balance de fuerzas de la Ec. 6-20 se reduce a: Ws  tanθ  =  aτL (6-26) El esfuerzo cortante que causa movimiento inmediato en una superficie plana es: τL  =  (Ws /a) tanθ (6-27) Combinando las ecuaciones 6-17, 6-25 y 6-27, la relación de fuerza cortante es:                                tan2φ K  =  cosφ  [ 1  -  _________ ] 1/2                                tan2θ (6-28) Se observa que K es una función de φ y θ únicamente. La Ec. 6-28 es equivalente a la siguiente ecuación, como se muestra en el siguiente recuadro:                       sen2φ K  =   [ 1  -  __________ ] 1/2                       sen2θ (6-29) Derivación de la Ec. 6-29 La Ecuación 6.28 se simplifica recurriendo a identidades trigonométricas establecidas:                                tan2φ K  =  cosφ  [ 1  -  _________ ] 1/2                                tan2θ (6-28a)                               cos2φ  tan2φ K  =   [ cos2φ  -  ________________ ] 1/2                                    tan2θ (6-28b)                               sen2φ K  =   [ cos2φ  -  _________ ] 1/2                               tan2θ (6-28c)                               sen2φ  cos2θ K  =   [ cos2φ  -  ________________ ] 1/2                                    sen2θ (6-28d)                                   sen2φ  (1 - sen2θ) K  =   [ 1 - sen2φ  -  _____________________ ] 1/2                                            sen2θ (6-28e)                       sen2φ K  =   [ 1  -  __________ ] 1/2                       sen2θ (6-29) 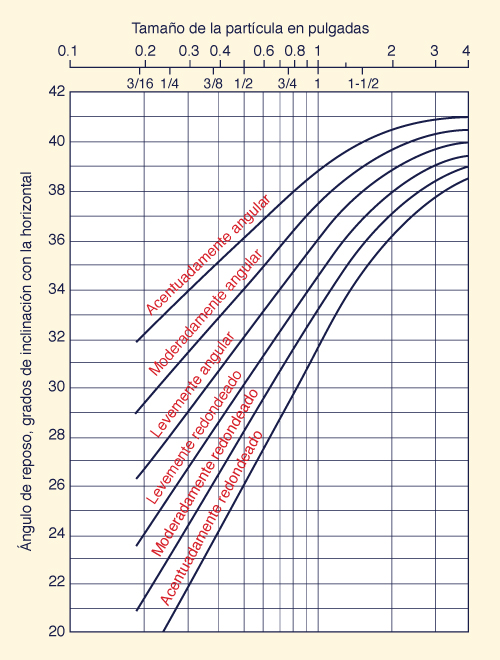Ángulo de reposo La Figura 6-25 muestra el ángulo de reposo de materiales no cohesivos, es decir, el ángulo θ de la Ec. 6-29. El tamaño de partícula (en pulgadas) es aquél para el cual el 25% del material, es mayor, en peso. Fig. 6-25  Ángulo de reposo de materiales no cohesivos (Chow, 1959). 6.4  FUERZA CORTANTE PERMISIBLE [Obras de Arte]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Canales No Erosionables]   [Canales Erosionables]   [Fuerza Cortante]   El método de fuerza cortante permisible se utiliza en el diseño de canales erosionables. El esfuerzo cortante permisible es el máximo que no cause erosión del material que forma el lecho del canal en una superficie plana. El valor, obtenido a partir de experimentos de laboratorio, se conoce como esfuerzo cortante crítico. 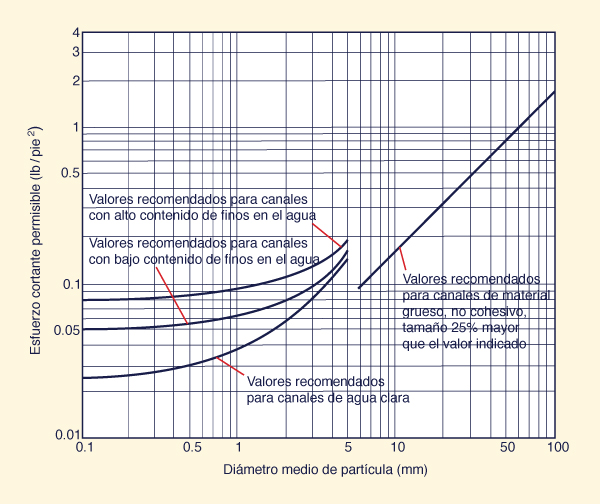La Figura 6-26 muestra el valor del esfuerzo cortante permisible para canales con materiales no cohesivos. Esta figura se puede utilizar para diámetros medios de partícula que varían en el rango de 0.1 a 100 mm. El lado izquierdo corresponde a materiales finos, no cohesivos (arena), con un diámetro aproximado de 0.1 a 5 mm. Se muestran tres curvas: La curva superior, adecuada para canales con alto contenido de sedimento fino (limo) en el agua; La curva media, adecuada para canales con bajo contenido de sedimentos finos (limo) en el agua; La curva inferior, adecuada para canales con agua libre de sedimentos. Debe tomarse en cuenta que mientras más limpia de sedimentos se encuentre el agua, mayor es su capacidad de recoger sedimentos del perímetro. Por lo tanto, en este caso, el esfuerzo cortante permisible debe ser menor. El lado derecho de la Fig. 6-26 se refiere a canales con material no cohesivo grueso, con un diámetro medio de 5 a 100 mm (de grava fina a muy gruesa, a piedras pequeñas). La línea que se muestra en la Fig. 6-26 es igual a 0.4 veces el diámetro de la partícula (en pulgadas) para el cual el 25% del material, por peso, es mayor; es decir, el esfuerzo cortante permisible es igual a 0.4 × d25 (in). Fig. 6-26  Esfuerzo cortante permisible para canales con materiales no cohesivos (Chow, 1959). 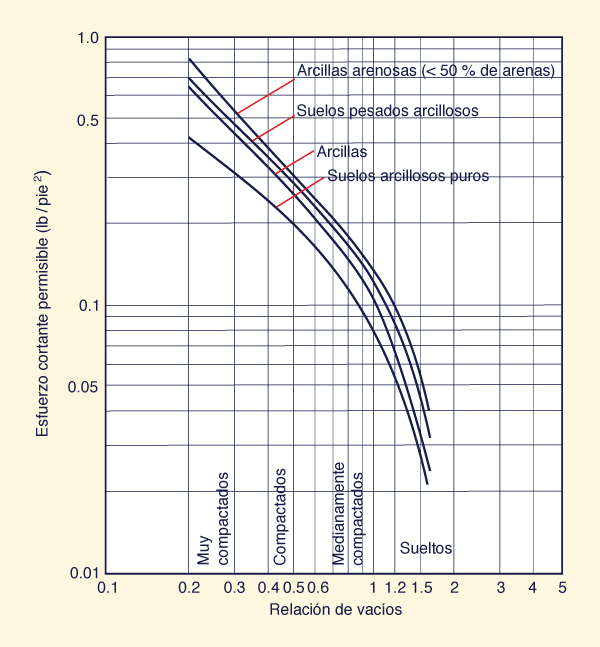Para materiales cohesivos, el esfuerzo cortante permisible es una función del tipo de suelo (arcillas arenosas a arcillas finas) y la relación de vacíos, como se muestra en la Fig. 6-27. Fig. 6-27  Esfuerzo cortante permisible para canales con materiales cohesivos (Chow, 1959). Los valores de las Figuras 6-26 y 6-27 corresponden a canales rectos. Para canales sinuosos, los valores de las figuras deben reducirse para tener en cuenta la socavación del banco. La Tabla 6-2 muestra los porcentajes de reducción recomendados para el esfuerzo cortante permisible en canales sinuosos. Tabla 6-2   Reducción del esfuerzo cortante permisible aplicable a canales sinuosos (Chow, 1959). Sinuosidad Reducción (%) Baja 10 Moderada 25 Alta 40 Método del esfuerzo cortante permisible El método del esfuerzo cortante permisible es un método de diseño de canales erosionables para estimar el material que forma el perímetro del canal. El valor del esfuerzo cortante permisible se determina experimentalmente o por experiencia. El procedimiento de cálculo, al igual que dos ejemplos prácticos, se detallan a continuación: Uso del mismo material en los taludes y el fondo, y Uso de un material en los taludes y otro en el fondo. A. Uso del mismo material en los taludes y el fondo Datos de entrada:  Descarga Q, pendiente de talud z, pendiente del canal S, y n de Manning; d25 de las partículas y la granulometría; el material en los taludes y el fondo es el mismo. Suponer b/y = 6, es decir, un valor razonable para comenzar. Suponer que el esfuerzo cortante en los taludes es el que controla el diseño. Éste es generalmente el caso cuando el material en los taludes y el fondo es el mismo. Con b/y y z, usar la Fig. 6-23 para determinar el valor de Cs (Cs es la ordenada de la Fig. 6-23) en la expresión para el esfuerzo cortante que actúa en los taludes: Ts = Cs γ y S. Con d25 y la granulometría, usar la Fig. 6-25 para encontrar el ángulo de reposo θ. Calcular la pendiente del talud: φ = tan-1 (1/z) Usar la Ec. 6-29 para calcular K. Utilizar la Fig. 6-26 para determinar el esfuerzo cortante permisible en el fondo τL. Calcular el esfuerzo cortante permisible en los taludes: τs = K τL. Establecer el esfuerzo cortante permisible superior o igual al esfuerzo cortante actuante: τs ≥ Ts; es decir, τs ≥ Cs γ y S Calcular la profundidad de flujo: y = τs / (Cs γ S) Calcular b: b = (b/y) y Con Q, b, z, n, y S conocidos, calcular la profundidad normal yn. Confirmar que yn ≤ y. De lo contrario, el valor asumido de b/y es demasiado pequeño. Por lo que se debe asumir un valor mayor y regresar al paso 11 haciendo iteraciones. Una vez cumplida la relación, establecer y = yn  y continuar con el siguiente paso. Con la última b/y y z, use la Fig. 6-22 para determinar el valor de Cb (la ordenada de la Fig. 6-22) en la expresión del esfuerzo cortante que actúa en el fondo TL = Cb γ y S. Calcular TL = Cb γ yn S Comparar TL calculada en el Paso 15 con τL calculada en el Paso 7. Si TL ≤ τL, los taludes controlan el diseño, como se supuso inicialmente. Aquí termina el cálculo. A. Ejemplo práctico Datos de entrada:  Q = 600 pies cúbicos por segundo; z = 2, pendiente de fondo S = 0.001, y n de Manning = 0.022; diámetro de la partícula d25 = 0.7 pulgadas, y granulometría ligeramente angular, el material en los taludes y en el fondo es el mismo. Asumir b/y = 6. Suponer que el esfuerzo cortante en los taludes controla el diseño. Con b/y = 6 y z = 2, usar la Fig. 6-23 para determinar el valor de Cs = 0.78. Con d25 = 0.7 pulgadas y granulometría ligeramente angular, usar la Fig. 6-25 para encontrar θ = 34°. φ = tan-1 (1/z) = 26.565° Usar la Ec. 6-29 para calcular K = 0.6. Usar d25 = 0.7 pulgadas en la Fig. 6-26 para determinar τL = 0.28 lbs/pie2. τs = K τL = 0.6 × 0.28 = 0.168 lbs/pie2. Establecer el esfuerzo cortante permisible igual o mayor al esfuerzo cortante actuante: τs = 0.168 ≥ Cs γ y S = (0.78) (62.4) y (0.001) Resolver para la profundidad de flujo: y ≤ 3.45 pies. Establecer la profundidad de flujo que se quiere alcanzar y = 3.45 pies. b = (6) (3.45) = 20.7. Redondear a b = 21 pies. Con Q = 600, b = 21, z = 2, n = 0.022, y S = 0.001, calcular la profundidad normal: yn = 4.536 pies. yn = 4.536 > y = 3.45. El ancho b es muy pequeño. Asumir (por prueba y error) b/y = 10. b = (10) (3.45) = 34.5. Redondear a b = 35 pies. Con una nueva b, resolver para la profundidad normal: yn = 3.376 pies. Ahora yn < y. Establecer y = 3.376 pies e ir al siguiente paso. Con b/y = 10 y z = 2, usar la Fig. 6-22 para determinar el valor de Cb = 1.0. Calcular TL = (1.0) (62.4) (3.376) (0.001) = 0.211 lbs/pie2. Comparar TL = 0.211 calculado en el Paso 15 con τL = 0.28 calculado en el Paso 7. TL = 0.211 < τL = 0.28; por lo tanto, los taludes controlan el diseño, como se supuso inicialmente. Aquí termina el cálculo. B. Un material en los taludes y otro en el fondo Entrada de datos:  Descarga Q, pendiente del talud z, pendiente del canal S, y n de Manning; material en los taludes y en el fondo son diferentes, especifique el tipo de material, tamaño de la partícula y forma de la granulometría, al igual que el contenido de sedimento fino si es necesario. Suponer b/y = 6, es decir, un valor razonable para empezar. Suponer que el esfuerzo cortante en los taludes controla el diseño. Éste es generalmente el caso cuando el material en los taludes y en el fondo es el mismo. Con b/y y z, usar la Fig. 6-23 para determinar el valor de Cs (Cs es la ordenada de la Fig. 6-23) en la expresión para el esfuerzo cortante que actúa en los taludes: Ts = Cs γ y S. Con d25 y la forma de la granulometría, usar la Fig. 6-25 para encontrar el ángulo de reposo θ. Calcular la pendiente del talud: φ = tan-1 (1/z) Usar la Ec. 6-29 para calcular K. Usar la Fig. 6-26 para determinar el esfuerzo cortante permisible en el fondo, de acuerdo al material en los taludes τLs (derecha de la Fig. 6-26), y el esfuerzo cortante permisible en el fondo de acuerdo al material en el fondo τLb (izquierda de la Fig. 6-26). Calcular el esfuerzo cortante permisible en los taludes: τs = K τLs. Establecer el esfuerzo cortante permisible mayor que o igual al esfuerzo cortante actuante: τs ≥ Ts; es decir, τs ≥ Cs γ y S Resolver para la profundidad de flujo: y = τs / (Cs γ S) Calcular b: b = (b/y) y Con Q, b, z, n, y S conocidos, resolver para la profundidad normal yn. Confirmar que yn ≤ y. De lo contrario, el valor asumido de b/y es demasiado pequeño. Asumir un valor mayor y regresar al Paso 11 e iterar. Una vez satisfecha la relación, establecer y = yn y proceder al siguiente paso. Con la última b/y y z, usar la Fig. 6-22 para determinar el valor de Cb (la ordenada de la Fig. 6-22) en la expresión para el esfuerzo cortante que actúa en el fondo TL = Cb γ y S. Calcular TL = Cb γ yn S Comparar TL calculada en el Paso 15 con τLb calculada en el Paso 7. Si TL ≤ τL, los taludes controlan el diseño, como se supuso inicialmente. En cambio, si TL > τL, el fondo controla el diseño. Si TL > τL, hacer que TL = τL. Resolver para la nueva y, confirmando que el fondo controla el diseño. Aquí termina el cálculo. B. Ejemplo practico Datos de entrada:  Q = 600 pies cúbicos por segundo; z = 2, pendiente del canal S = 0.001, y n de Manning = 0.022; material en los taludes: no cohesivo, d25 = 0.7 pulgadas, forma de la granulometría ligeramente angular; material en el fondo: no cohesivo, d60 = 0.8 mm, con alto contenido de sedimento fino en el agua. Suponer b/y = 6. Suponer que el esfuerzo cortante en los taludes está controlando el diseño. Con b/y = 6 y z = 2, usar la Fig. 6-23 para determinar el valor de Cs = 0.78. Con d25 = 0.7 pulgadas y forma de la granulometría ligeramente angular, usar la Fig. 6-25 para encontrar θ = 34°. φ = tan-1 (1/z) = 26.565° Usar la Ec. 6-29 para calcular K = 0.6. Usar la Fig. 6-26 (derecha) para determinar τLs = 0.28 lbs/pies2; usar la Fig. 6-26 (izquierda) para determinar τLb = 0.09 lbs/pies2. τs = K τLs = 0.6 × 0.28 = 0.168 lbs/pies2. Establecer el esfuerzo cortante permisible mayor que o igual al esfuerzo cortante actuante: τs = 0.168 ≥ Cs γ y S = (0.78) (62.4) y (0.001) Resolver para la profundidad de flujo: y ≤ 3.45 pies. b = (6) (3.45) = 20.7. Redondear a b = 21 pies. Con Q = 600, b = 21, z = 2, n = 0.022, y S = 0.001, resolver para la profundidad normal: yn = 4.536 pies. yn = 4.536 > y = 3.45 pies. El ancho b es muy pequeño. Asumir (por prueba y error) b/y = 10. b = (10) (3.45) = 34.5. Redondear a b = 35 pies. Con el nuevo b, resolver para la profundidad normal: yn = 3.376 pies. Ahora yn < y. Establecer y = 3.376 pies e ir al siguiente paso. Con b/y = 10 y z = 2, usar la Fig. 6-22 para determinar el valor de Cb = 1.0. Calcular TL = (1.0)(62.4)(3.376)(0.001) = 0.211 lbs/pies2. Comparar TL = 0.211 calculada en el Paso 15 con τLb = 0.09 calculada en el Paso 7. TL = 0.211 > τL = 0.09; por lo tanto, el fondo controla el diseño. Hacer que TL = Cb γ yn S = (1.0)(62.4) y (0.001) = 0.09. Por lo tanto: y = 1.44 pies. Asumir (por prueba y error) b/y = 106. Por lo tanto: b = 154 pies. Con Q = 600, b = 152, z = 2, S = 0.001, y n = 0.022, calcular y = 1.44 pies. El diseño es correcto. Aquí termina el cálculo. 6.5  OBRAS DE ARTE [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Canales No Erosionales]   [Canales Erosionales]   [Fuerza Cortante]   [Fuerza Cortante Permisible]   Otros componentes hidráulicos en el diseño de canales incluyen caídas, cruces de arroyos, estructuras de disipación, y estructuras de control de gradiente. Las Figuras 6-28 a 6-34 muestran algunos ejemplos ilustrativos. . Fig. 6-28  Una serie de caídas con el propósito de controlar la inestabilidad del flujo en el proyecto de irrigación Cabana-Mañazo, Puno, Perú. Fig. 6-29  Cruce del canal de alimentación del reservorio Tinajones a través del Arroyo Chiriquipe, Lambayeque, Perú. Fig. 6-30   Cruce de un arroyo local con el Canal Wellton-Mohawk, Wellton, Arizona. Fig. 6-31   Cruce de un arroyo por medio de un sifón, proyecto de irrigación Cabana-Mañazo, Puno, Perú. Fig. 6-32  Cruce del Canal Todo-Americano con el Rio Nuevo mediante un sifón de gran tamaño, cerca de Calexico, Valle Imperial, California. Fig. 6-33  Estructura de disipación, Río Chonta, Cajamarca, Perú. Fig. 6-34   Estructura de control de gradiente, Río Caquezá, Cundinamarca, Colombia. PREGUNTAS [Problemas]   [Bibliografía]   •   [Arriba]   [Canales No Erosionables]   [Canales Erosionables]   [Fuerza Cortante]   [Fuerza Cortante Permisible]   [Obras de Arte]   ¿Qué determina la rugosidad de la superficie en un canal artificial? ¿Qué es el bordo libre en el diseño de un canal? ¿Cuál es la abscisa en el diagrama de Shields? ¿Cuál es la ordenada en el diagrama de Shields? ¿Qué número de Froude generalmente asegura el inicio de movimiento? ¿Cómo se reconcilian las velocidades máximas y mínimas permisibles en el diseño de un canal? ¿Cómo está relacionada la velocidad máxima permisible con el esfuerzo cortante? ¿Cuál es el valor máximo del coeficiente Cs para el esfuerzo cortante en los taludes de un canal? ¿Cuál es el rango de valores del ángulo de reposo en materiales no cohesivos? ¿Cómo se define la relación de fuerza cortante? ¿Cómo afecta el contenido de sedimentos finos en el agua al valor de esfuerzo cortante permisible? ¿Cuándo se justifica una estructura de control del nivel del suelo? PROBLEMAS [Bibliografía]   •   [Arriba]   [Canales No Erosionables]   [Canales Erosionables]   [Fuerza Cortante]   [Fuerza Cortante Permisible]   [Obras de Arte]   [Preguntas]   ¿Cuál es la velocidad mínima permisible para una partícula de diámetro ds = 0.6 mm y un factor de fricción de Chezy adimensional (Darcy-Weisbach modificado) f = 0.004? ¿Cuál es el número de Froude mínimo y la velocidad mínima permisible para una partícula de diámetro de ds = 0.6 mm, factor de fricción de Chezy adimensional f = 0.004, profundidad hidráulica D = 1 m, y temperatura del agua T = 20°C? ¿Cuál es el número de Froude mínimo y la velocidad mínima permisible para una partícula de diámetro ds = 0.3 mm, factor de fricción de Chezy adimensional f = 0.003, profundidad hidráulica D = 3 pies, y temperatura del agua T = 68°F? Un canal tiene los siguientes datos:   Q = 330 pies cúbicos por segundo, z = 2, n = 0.025, y S = 0.0018. Utilizar el método del esfuerzo cortante para calcular el ancho de fondo y la profundidad de flujo bajo las siguientes condiciones: Las partículas son las mismas en los taludes y en el fondo: moderadamente angulares y de tamaño d25 = 0.9 pulgadas. Igual que en (a), pero con partículas moderadamente redondeadas. Comentar cómo la forma de las partículas afecta al diseño. Verificar con FUERZA DE TRACCIÓN EN LÍNEA. Un canal tiene los siguientes datos:   Q = 220 m3/s, z = 2, n = 0.03, y S = 0.0006. Utilizar el método del esfuerzo cortante para calcular el ancho de fondo y la profundidad bajo las siguientes condiciones: Las partículas en los taludes son ligeramente angulares y de diámetro d25 = 35 mm; las partículas en el fondo son de diámetro d50 = 5 mm. Las partículas en los taludes son las mismas que en (a), pero las partículas en el fondo son más pequeñas, con diámetro d50 = 4 mm. Ambos casos (a) y (b) presentan bajo contenido de sedimento fino en el agua, y la sinuosidad del canal es despreciable. Comentar cómo el tamaño de la partícula en el fondo afecta al diseño. Verificar con FUERZA DE TRACCIÓN EN LÍNEA. Un cierto tipo de césped tiene un esfuerzo cortante crítico τc = 30 N/m2. El factor de fricción de Chezy adimensional es f = 0.0075. ¿Cuál es la velocidad crítica? BIBLIOGRAFÍA •   [Arriba]   [Canales No Erosionables]   [Canales Erosionables]   [Fuerza Cortante]   [Fuerza Cortante Permisible]   [Obras de Arte]   [Preguntas]   [Problemas]   American Society of Civil Engineers, 1975. Sedimentation Engineering. Manual de Práctica No. 54. Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, Nueva York. Ponce, V. M. 1989. Engineering Hydrology, Principles and Practices. Prentice Hall, Englewood Cliffs, Nueva Jersey. http://hidraulicadecanales.sdsu.edu 200206