[Alcantarillas]   [Control en la Entrada]   [Control en la Salida]   [Diseño de Alcantarillas]   [Preguntas]   [Problemas]   [Bibliografía]   •   CAPÍTULO 8: HIDRÁULICA DE ALCANTARILLAS 8.1 ALCANTARILLAS  [Control en la Entrada]   [Control en la Salida]   [Diseño de Alcantarillas]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   Las alcantarillas son conductos de drenaje de longitud corta, ubicados en las intersecciones de la red de drenaje con la red de transporte (carreteras, caminos, vías de ferrocarril, etc.). Las alcantarillas son mucho más pequeñas que los puentes; por consiguiente, hay un mayor número de ellas. Usualmente están diseñadas para operar bajo flujo permanente gradualmente variado; por lo tanto se aplican los principios del Capítulo 7. 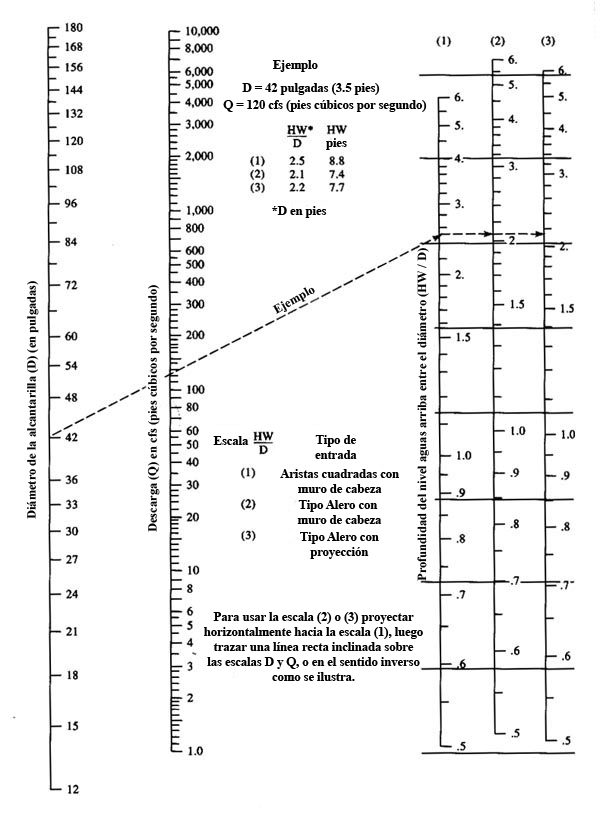Las alcantarillas se calculan para pasar el gasto de diseño sin producir un desbordamiento tal que comprometa la integridad de la superestructura. El gasto de diseño se basa en consideraciones hidrológicas. El período de retorno (el cual es el recíproco de la frecuencia) varía típicamente entre 10 y 50 años (Ponce, 2008). A mayor período de retorno, mayor será el gasto de diseño y, consecuentemente, mayor serán las dimensiones de la estructura (Fig. 8-1). Fig. 8-1  La alcantarilla del Cañón Yogurt, en la frontera internacional entre California, EE.UU. y Baja California, México. El flujo en una alcantarilla depende de lo siguiente: El tamaño y forma de la sección transversal, La pendiente de fondo, La longitud del conducto, La rugosidad del conducto, y Las características de la entrada y salida. El flujo en una alcantarilla puede ser de los siguientes tipos: De superficie libre (flujo en canal), De conducto cerrado (flujo en tubería), o De superficie libre en una parte de su longitus, y conducto cerrado en otra parte. Las profundidades de flujo aguas arriba y aguas abajo determinan si la alcantarilla está fluyendo parcial o completamente llena. La profundidad de flujo aguas arriba, por encima de la base o fondo de la alcantarilla en la entrada, es denominada headwater HW, por sus siglas en Inglés. La profundidad de flujo aguas abajo, por encima de la base o fondo de la alcantarilla en la salida, es denominada tailwater TW. El objetivo es calcular el tamaño más pequeño (de la sección transversal) de la alcantarilla que pueda pasar el gasto de diseño sin superar una profundidad aguas arriba determinada (Fig. 8-2). El diseño depende si el control está en la entrada o la salida. Fig. 8-2  Alcantarilla debajo de la linea de ferrocarril, Cañada Joe Bill, Tecate, Baja California, México. 8.2  CONTROL EN LA ENTRADA [Control en la Salida]   [Diseño de Alcantarillas]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Alcantarillas]   El flujo en una alcantarilla se encuentra bajo control en la entrada cuando la descarga depende sólo de las condiciones en la entrada. Por ejemplo, asumir una alcantarilla circular de diámetro D, longitud L, pendiente de fondo S, profundidad aguas arriba HW, y profundidad aguas abajo TW. El primer paso es calcular la profundidad normal yn y la profundidad crítica yc. Se examinan las siguientes situaciones: Si yn < yc, el flujo en el conducto es supercrítico y la profundidad aguas abajo no afecta a las condiciones aguas arriba. Por lo tanto, la profundidad aguas arriba está exclusivamente controlada por las condiciones en la entrada (Fig. 8-3). 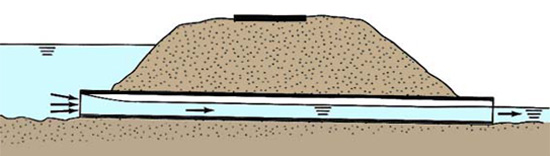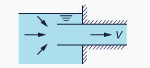Fig. 8-3  Flujo en una alcantarilla bajo condiciones supercríticas, con la entrada sumergida y la salida no sumergida. 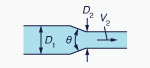Si el flujo es supercrítico y TW > yn, puede ocurrir un salto hidráulico en algún lugar del conducto (Fig. 8-4). Fig. 8-4  Flujo en una alcantarilla bajo condiciones supercríticas, con la entrada no sumergida y la salida sumergida. El control en la entrada ocurre cuando la alcantarilla es capaz de conducir más flujo que el permitido por el orificio de entrada. La sección de control se sitúa precisamente en la entrada. El flujo pasa de profundidad crítica en la sección de control a supercrítica aguas abajo de la misma. Cuando el control está en la entrada, la alcantarilla actúa como un orificio o vertedero. Si la entrada está sumergida, el flujo es similar al de un orificio; por el contrario, si la entrada no está sumergida, el flujo se asemeja al de un vertedero. [Si HW < 1.2 D, la entrada será no sumergida]. Si la entrada no está sumergida pero la salida sí está, se formará un salto hidráulico en algún lugar del conducto (Fig. 8-4). 8.3  CONTROL EN LA SALIDA [Diseño de Alcantarillas]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Alcantarillas]   [Control en la Entrada]   El control en la salida ocurre en las siguientes condiciones: Cuando la profundidad aguas abajo TW es: TW > 1.2 D; es decir, para un nivel alto de la superficie de agua. En este caso, la alcantarilla está completamente sumergida, lo cual se asemeja a un flujo en conducto cerrado. El nivel aguas arriba puede calcularse usando la ecuación de la conservación de la energía. El nivel aguas arriba está determinado por la elevación del nivel aguas abajo y las características de fricción de la alcantarilla. Cuando la entrada y la salida se encuentran sumergidas; y Cuando la pendiente de la alcantarilla es leve (flujo subcrítico) y tanto el nivel aguas arriba como el nivel aguas abajo son menores que el diámetro de la alcantarilla (HW < D; TW < D). En este caso, el procedimiento más apropriado es calcular el perfil de la superficie del agua. 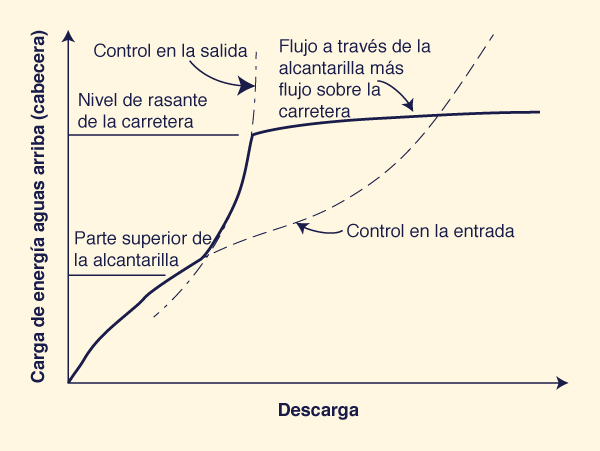La Figura 8-5 ilustra la variación de la descarga o caudal en función de la carga o nivel de energía aguas arriba. Puede observarse que conforme la descarga aumenta de baja a alta, a un cierto nivel el flujo cambia repentinamente de control en la entrada a control en la salida. Fig. 8-5  Variación de la descarga en función de la carga (nivel) de energía aguas arriba (U.S. Army Corps of Engineers, 2014). 8.4  DISEÑO DE ALCANTARILLAS [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Alcantarillas]   [Control en la Entrada]   [Control en la Salida]   El diseño de una alcantarilla requiere de los siguientes pasos: Coleccionar los datos de diseño: Descarga o gasto, Elevación del nivel aguas abajo, y Pendiente del conducto. Elegir el tipo y características de alcantarilla: Forma de la sección transversal (circular, cuadrada, rectangular, con arco), Dimensiones (diámetro, si es circular), Longitud del conducto, Tipo de material (Figs. 8-6 y 8-7) (concreto, acero corrugado, aluminio corrugado, mampostería de piedra), y Tipo de entrada (con esquinas rectas o esquinas redondeadas). Fig. 8-6  Un conjunto de dos alcantarillas de acero corrugado. Determinar el tipo de control predominante (entrada o salida), basado en: (a) la elevación del nivel aguas arriba, (b) la elevación del nivel aguas abajo, (c) el diámetro, y (d) la pendiente. Si el control es en la entrada, calcular la elevación del nivel aguas arriba requerida para pasar el gasto de diseño. Si el control es en la salida, calcular la elevación del nivel aguas arriba requerida, usando: (a) la ecuación de conservación de la energía, o (b) el cálculo del perfil de la superficie del agua. Si la elevación calculada del nivel aguas arriba es mayor que la permitida, elegir una alcantarilla de mayor tamaño y repetir el proceso de cálculo. En algunos casos, no es posible determinar el tipo de control de antemano. En este caso, se recomienda hacer los dos cálculos. El tipo de control adoptado será aquél que resulte en una mayor elevación del nivel aguas arriba. Otras consideraciones en el diseño de una alcantarilla incluyen: Socavación o erosión en el cuerpo del terraplén que rodea al conducto, Socavación local en la salida de la alcantarilla, Erosión del material de relleno cerca de la entrada, Obstrucción del conducto con escombros, y Provisión para el paso de peces. Fig. 8-7  Cruce de carretera con una alcantarilla rectangular de mampostería de piedra. Ejemplo de diseño usando conservación de la energía Diseñar una alcantarilla para las siguientes condiciones: Gasto de diseño:  Q = 200 pies cúbicos por segundo. Período de retorno:  T = 25 años. Longitud del conducto:  L = 200 pies. Pendiente de fondo:  So = 0.01. Tipo de alcantarilla:  Concreto. n de Manning = 0.013. Elevación de la base en la entrada:  z1 = 100 pies. Elevación de la rasante de la carretera suprayacente:  Es = 110 pies. Profundidad aguas abajo:  TW = y2 = 3.5 pies. Bordo libre:  Fb = 2 pies. Solución La elevación de diseño en el extremo aguas arriba es:  Es - Fb = 100 - 2 = 108 pies. Suponer una tubería de concreto circular, con esquinas rectas y muros de cabecera. Suponer que el control está en la salida. Suponer que la línea de gradiente hidráulica (HGL) está en la elevación del extremo aguas abajo. Calcular la elevación en la salida: z2 = z1 - (So L) = 100 - (0.01 × 200) = 98 pies. Calcular la elevación del nivel aguas abajo:  z2 + y2 = 98 + 3.5 = 101.5 pies. Establecer la conservación de la energía (Fig. 8-8):                      V12                             V22 z1  +  y1  +   _____  =  z2  +  y2  +   _____  +  ∑hL                       2g                              2g (8-1) Fig. 8-8  Conservación de la energía en el flujo de una alcantarilla. Suponer V1 = 0, es decir, la velocidad es cero en el extremo aguas arriba. Suponer V2 = 0, es decir, la velocidad se disipa a cero en el extremo aguas abajo. La pérdida de carga ∑hL es igual a la suma de las pérdidas en la entrada (con coeficiente de pérdida Ke), pérdidas en la salida (con coeficiente de pérdida KE), y pérdidas a lo largo del conducto. Usando la ecuación de Darcy-Weisbach, la pérdida de carga es:                                                       V 2 ∑hL  =  [ (Ke  +  KE  +  f (L / D ) ] _____                                                       2g (8-2) De la Tabla 8-1, asumir Ke = 0.5 y KE = 1 (Roberson et al., 1998). Tabla 8-1  Coeficientes de pérdida de carga en la entrada, contracción, y expansión. Descripción Ilustración (Hacer click en la figura para mostrar) Datos adicionales Coeficiente de pérdida de cargaK Entrada hL = Ke [V 2/(2g)] r /d Ke 0.0 0.50 0.1 0.12 > 0.2 0.03   1.0 Contracción hL = KC [V22/(2g)] D2 /D1 KC θ = 60° KC θ = 180° 0.0 0.08 0.50 0.2 0.08 0.49 0.4 0.07 0.42 0.6 0.06 0.32 0.8 0.05 0.18 0.9 0.04 0.10 Expansión hL = KE [V12/(2g)] D1 /D2 KE θ = 10° KE θ = 180° 0.0   1.00 0.2 0.13 0.92 0.4 0.11 0.72 0.6 0.06 0.42 0.8 0.03 0.16 La relación entre el factor de fricción de Darcy-Weisbach f y el n de Manning es (Capítulo 5):            8 g n 2 f  =  __________           k 2R 1/3 (8-3) en la cual k = 1 en unidades SI, y k = 1.486 en las unidades acostumbradas en EE.UU. En las unidades acostumbradas en EE.UU., con k = 1.486, y g = 32.17 pies/s2:           116.55 n 2 f  =  ____________              R 1/3 (8-4) Para un tubo circular: R = D / 4. Por lo tanto:          185.01 n 2 f  =  ____________              D 1/3 (8-5) De la Ec. 8-1, la conservación de la energía se reduce a:                                                    z1  +  y1  =  z2  +  y2  +  ∑hL                        (8-6)                                                    108  =  101.5  +  ∑hL                        (8-7) La ecuación de pérdida de carga (Ec. 8-2) se repite aquí por conveniencia:                                                       V 2 ∑hL  =  [ (Ke  +  KE  +  f (L / D ) ] _____                                                       2g (8-2) Reemplazando la Ec. 8-5 en la Ec. 8-2:                                                                            V 2 ∑hL  =  [ 0.5  +  1.0  +  (185.01 n 2 L / D 4/3 ) ] _____                                                                            2g (8-8) Combinando las Ecs. 8-7 y 8-8:                                                     V 2 6.5  =  [ 1.5  +  (6.253 / D 4/3 ) ] _____                                                     2g (8-9) La velocidad de flujo es:  V = Q / A. Por lo tanto: V = 200 / A = 200 / [ (π/4) D 2 ] La carga de velocidad es:  V 2 / (2g) = { 2002 / [ (π/4)2 D 4 ] } / (2g) = 1008 / D 4 Reemplazando la carga de velocidad en la Ec. 8-9:                                                     1008 6.5  =  [ 1.5  +  (6.253 / D 4/3 ) ] _______                                                       D 4 (8-10) Resolviendo la Ec. 8-10 por iteración: D = 4.38 pies. Para propósitos de diseño, asumir el siguiente tamaño por exceso:  D = 4.5 pies. Con Q = 200 pies cúbicos por segundo, D = 4.5 ft = 54 pulgadas, usar la Fig. 8-9 para encontrar la relación HW/D, es decir, la profundidad aguas arriba dividida entre el diámetro. En este caso: HW/D = 2.2, para una alcantarilla de aristas cuadradas con muros de cabeza [Escala (1)]. Fig. 8-9  Relación profundidad aguas arriba a diámetro (HW/D) para alcantarillas de concreto y control en la entrada. La profundidad aguas arriba es:  HW = (HW/D) × D = 2.2 × 4.5 = 9.9 pies. La elevación del nivel aguas arriba es:   100 + 9.9 = 109.9 pies. Esta elevación es mayor que 108 pies, lo cual es muy alto. Por lo tanto el diámetro seleccionado D = 4.5 pies es demasiado pequeño. Probar con el siguiente tamaño:  D = 5 pies. Con Q = 200 pies cúbicos por segundo, D = 5 pies = 60 pulgadas, usar la Fig. 8-9 para encontrar la relación de la profundidad aguas arriba dividida entre el diámetro HW/D = 1.6, para una alcantarilla de aristas cuadradas con muros de cabeza [Escala (1)]. La profundidad del nivel aguas arriba es:  HW = HW/D × D = 1.6 × 5 = 8 pies. La elevación aguas arriba es:   100 + 8 = 108 pies. Esta elevación es la misma que la de la elevación de diseño; por lo tanto, el diseño está correcto. Calcular la profundidad normal usando CANAL EN LÍNEA 06:  yn = 3.284 pies. Calcular la profundidad crítica usando CANAL EN LÍNEA 07:  yc = 4.037 pies. Dado que yn < yc, el flujo es supercrítico. Dado que TW = 3.5 > yn = 3.284, habrá un pequeño salto hidráulico cerca de la salida. El flujo es supercrítico a lo largo de gran parte del conducto. Por lo tanto, se concluye que el control se encuentra en la entrada. El diámetro de diseño es:  D = 5 pies = 60 pulgadas.  RESPUESTA. PREGUNTAS [Problemas]   [Bibliografía]   •   [Arriba]   [Alcantarillas]   [Control en la Entrada]   [Control en la Salida]   [Diseño de Alcantarillas]   ¿Qué es una alcantarilla? ¿Cuál es el período de retorno típico en el diseño de alcantarillas? ¿Cuándo se encuentra una alcantarilla bajo control en la entrada? ¿Cuándo se encuentra una alcantarilla bajo control en la salida? Enumere las variables hidráulicas que afectan al flujo en una alcantarilla. Enumere otras consideraciones en el diseño de alcantarillas. PROBLEMAS [Bibliografía]   •   [Arriba]   [Alcantarillas]   [Control en la Entrada]   [Control en la Salida]   [Diseño de Alcantarillas]   [Preguntas]   Diseñar una alcantarilla de concreto circular con los siguientes datos:  Q = 300 pies cúbicos por segundo; elevación de la base en la entrada z1 = 100 pies; profundidad aguas abajo y2 = 4 pies; pendiente del conducto So = 0.02; longitud del conducto L = 200 pies; n de Manning = 0.013; elevación de la rasante de la carretera Er = 112 pies; bordo libre Fb = 2 pies. El tipo de entrada es de esquinas rectas con muros de cabecera (Fig. 8-10). Usar CANAL EN LÍNEA 06 para calcular la profundidad normal y CANAL EN LÍNEA 07 para calcular la profundidad crítica. Fig. 8-10   Alcantarilla típica de cruce de carretera. Diseñar una alcantarilla de concreto circular con los siguientes datos:  Q = 500 pies cúbicos por segundo; elevación de la base en la entrada z1 = 100 pies; profundidad aguas abajo y2 = 4 pies; pendiente del conducto So = 0.01; longitud del conducto L = 200 pies; n de Manning = 0.013; elevación de la base de la carretera Er = 115 pies; bordo libre Fb = 2 pies. El tipo de entrada es de esquinas rectas con muros de cabecera. Usar CANAL EN LÍNEA 06 para calcular la profundidad normal y CANAL EN LÍNEA 07 para calcular la profundidad crítica. Verificar el diseño usando ALCANTARILLA EN LÍNEA. BIBLIOGRAFÍA •   [Arriba]   [Alcantarillas]   [Control en la Entrada]   [Control en la Salida]   [Diseño de Alcantarillas]   [Preguntas]   [Problemas]   Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, Nueva York. Ponce, V. M. 2008. Preguntas y respuestas sobre el período de retorno a ser usado para diseño. Artículo en línea. Roberson, J. A., J. J. Cassidy, and M. H. Chaudhry. 1998. Hydraulic Engineering, Second edition, Wiley. U.S. Army Corps of Engineers. 2014. HEC-RAS River Analysis System. Version 4.1, Hydrologic Engineering Center, Davis, California. http://hidraulicadecanales.sdsu.edu 200509 10:00