1. TRES VELOCIDADES CARACTERÍSTICAS EN EL FLUJO DE UN CANAL ABIERTO Hay tres velocidades características en el flujo de un canal abierto (Ponce 1991):
La ecuación de Manning es (Chow 1959):
en la cual u = la velocidad media del flujo uniforme permanente, R = radio hidráulico, S = pendiente de fricción (o de fondo), y n = coeficiente de fricción de Manning. La ecuación de Chezy es (Chow 1959):
en la cual C = Coeficiente de fricción de Chezy. La fórmula de Seddon expresa la celeridad de la onda cinemática ck de la siguiente manera (Seddon 1900; Chow 1959):
en la cual T = ancho superior de la sección del canal, Q = caudal, y y = profundidad de flujo.
La fórmula de Seddon se expresa alternativamente como sigue (Ponce 1989):
en la cual β = exponente en la curva de gasto:
La celeridad de la onda cinemática relativa v, o celeridad de Seddon relativa al flujo, es:
La celeridad de la onda dinámica relativa w, o celeridad de Lagrange relativa al flujo, es (Chow 1959):
en la cual g = aceleración de la gravedad, y y = profundidad de flujo. 2. DOS NÚMEROS ADIMENSIONALES EN EL FLUJO DE UN CANAL ABIERTO Las tres velocidades u, v y w, expresadas por las ecuaciones. 1 o 2, y 6 y 7, respectivamente, dan lugar a dos números adimensionales independientes, los números de Froude y Vedernikov (Powell 1948; Ponce 1991). El tercer número, o tercera combinación posible, se expresa en términos de los otros dos. El número de Froude es la relación entre u y w:
El número de Vedernikov es la relación entre v y w:
El tercer número es la relación entre v y u:
Téngase en cuenta que la cantidad β - 1 también es igual a la relación de los números de Vedernikov y Froude. Una vez que se conocen dos de estos números, se puede determinar el tercero.
El número de Froude describe la condición de flujo: (1) subcrítico, (2) crítico o (3) supercrítico (Chow 1959). Bajo flujo subcrítico, las ondas dinámicas pueden viajar río arriba porque u < (g y)1/2. Bajo flujo supercrítico, las ondas dinámicas no pueden viajar río arriba porque
El número de Vedernikov describe la condición de flujo: (1) estable, (2) neutral o (3) inestable (Chow 1959). Bajo flujo estable, las ondas cinemáticas viajan más lentamente que las ondas dinámicas porque v < (g y)1/2. Bajo flujo inestable, las ondas cinemáticas viajan más rápido que las ondas dinámicas porque v > (g y)1/2. Bajo flujo neutral, las ondas cinemáticas viajan a la misma velocidad que las ondas dinámicas porque v = (g y)1/2. Cuando V ≥ 1, las condiciones de flujo son tales que se forman ondas pulsantes o de rollo en el flujo de canal abierto. En la práctica, las ondas de rollo aparecen como un tren de pequeñas ondas superficiales que viajan abajo en un flujo de canal abierto; ver Fig. 1. El flujo neutro caracteriza la condición bajo la cual las ondas cinemáticas, que transportan masa, viajan a la misma velocidad que las ondas dinámicas, que transportan energía
(Lighthill y Whitham 1955; Ponce 1992).
El parámetro β caracteriza el tipo de fricción y la forma de la sección transversal; por ejemplo, β = 4/3 es aplicable a la fricción de Manning en un canal triangular. Para un tipo dado de fricción y forma de sección transversal, se establece el valor de β. El número de Froude de estabilidad neutra Fns es el que corresponde al número de Vedernikov V = 1. El número de Froude de estabilidad neutra es una función sólo de β. De la Ec. 10, el número de Froude de estabilidad neutral es el siguiente:
La Tabla 1 muestra valores de Fns para valores seleccionados de β correspondientes a combinaciones típicas de tipos de fricción y forma de sección transversal, de un valor alto de
La Tabla 1 muestra que el valor β = 1 representa un comportamiento asintótico, ya que para
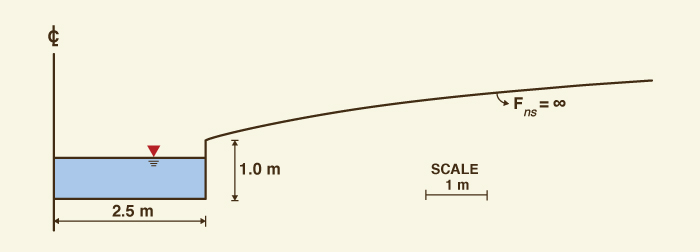
De la Ecuación 5, para β = 1, la velocidad del flujo es una constante, β = Q/A. Por lo tanto, un canal inherentemente estable es aquél en el que la velocidad del flujo y el radio hidráulico permanecen constantes a medida que varía la profundidad (Liggett 1975). La forma del canal inherentemente estable ha sido documentada por Ponce y Porras (1993) (Fig. 2).
3. VEN TE CHOW: UNA SINOPSIS
Ven Te Chow nació en Hangchow, China, el 14 de agosto de 1919 (Fig. 3). Recibió su grado de Bachiller en ingeniería civil de la Universidad Nacional Chiao Tung en 1940, su maestría en mecánica de ingeniería de la Universidad Estatal de Pensilvania en 1948, y su doctorado en ingeniería hidráulica de la Universidad de Illinois en 1950 (Ackermann 1984). Adquirió la ciudadanía estadounidense en 1962 y estuvo en la facultad de ingeniería civil de la Universidad de Illinois desde 1948 hasta su falllecimiento en 1981.
Chow es autor de los siguientes libros: (1) Hidráulica de Canales Abiertos, publicado en 1959, del cual se extrajo la Fig. 4; (2) Manual de Hidrología Aplicada, publicado en 1964; y (3) Hidrología Aplicada, con los coautores David Maidment y Larry Mays, publicado en 1989.
4. EL NÚMERO DE FROUDE
El número de Froude se atribuye a William Froude, quien nació en Dartington, Devon, Inglaterra en 1810, y murió de un derrame cerebral en un crucero a Sudáfrica en 1879, a la edad de 69 años (Fig. 5).
En 1861, Froude escribió un artículo sobre el diseño de la estabilidad de los barcos en una vía marítima. Más tarde, entre 1863 y 1867, trabajando con modelos físicos de barcos, demostró que la resistencia por fricción en el modelo (a escala reducida) y el prototipo (el barco real) eran iguales cuando la velocidad V era proporcional a la eslora L, de la nave, a la potencia 1/2:
en al cual k es una constante que se aplica tanto al modelo como al prototipo. Froude llamó a esta ley física la "Ley de Comparación". Fue el primero en identificar la forma más eficiente para el casco de los barcos, así como en predecir la estabilidad del barco basándose en estudios con modelos a escala reducida (Fig. 6).
En la hidráulica de canales abiertos, la Ley de Froude está incorporada en el número de Froude, definido de la siguiente manera (Chow 1959; Brater y King 1976):
en la cual D es la profundidad hidráulica, definida como el área de flujo dividida por el ancho superior. Nótese que para la aplicación al flujo en canales abiertos, la longitud horizontal L de la Ley de Froude (Ec. 12) ha sido reemplazada por la profundidad hidráulica D (Ec. 13).
El cálculo del número de Froude se puede realizar en línea usando ONLINE FROUDE.
5. EL NÚMERO DE VEDERNIKOV
El concepto del número de Vedernikov se publicó por primera vez en una revista soviética (Vedernikov 1945; 1946) (Fig. 7). Craya escribió sobre el mismo concepto en un artículo publicado en 1952 (Craya 1952). El criterio de Vedernikov-Craya establece que las ondas de rollo se formarán cuando la celeridad de Seddon iguale o supere la celeridad de Lagrange, es decir, cuando la celeridad de la onda cinemática, gobernada por la gravedad y la fricción, supere la celeridad de la onda dinámica, gobernada por el gradiente de presiones y la inercia. Ésta es la condición de que el número de Vedernikov V ≥ 1.
Téngase en cuenta la desafortunada confusión en el artículo de Craya, en la cual la celeridad de Lagrange [onda dinámica] se describe como gobernada por la gravedad [sic] y la inercia. El papel de las diversas fuerzas que actúan en el flujo no estacionario en canales abiertos (gravedad, fricción, gradiente de presiones e inercia) ha sido aclarado por Ponce y Simons (1977), quienes calcularon la celeridad de onda relativa adimensional en todo el espectro de número de onda adimensional. Bajo la fricción de Chezy, para el número de Froude F = 2, es decir, V = 1, todas las ondas se propagan con la misma celeridad, independientemente del tamaño.
Para reiterar, el criterio de Vedernikov-Craya establece que las ondas de rollo se formarán en un canal abierto bajo la siguiente condición, en términos de celeridades absolutas:
En términos de celeridades relativas, las ondas de rollo se formarán cuando la celeridad relativa de Seddon sea mayor o igual a la celeridad relativa de Lagrange:
La Figura 8 muestra la formación de ondas en el aliviadero del embalse Turner, en el condado de San Diego, California, luego del rebalse después de fuertes lluvias, el 24 de febrero de 2005. Téngase en cuenta que la condición de no deslizamiento en las paredes verticales hace que las ondas parezcan como si el flujo fuera tridimensional.
El cálculo del número de Vedernikov se puede realizar en línea usando ENLINEA VEDERNIKOV.
6. EL NÚMERO DE VEDERNIKOV EN CHOW EN
HIDRAULICA DE CANALES ABIERTOS
En la sección 8-8, Inestabilidad de flujo uniforme, de Hidráulica de Canales Abiertos, Ven Te Chow describe un criterio "que puede llamarse el número de Vedernikov" de la siguiente manera (Powell, 1948):
en la cual x = exponente del radio hidráulico R en la fórmula general de velocidad u = f (R), definido de la siguiente manera:
en la cual b = exponente del número de Reynolds R en la ley de fricción
El parámetro γ es un factor de forma de la sección transversal definido de la siguiente manera:
en la cual R = radio hidráulico; P = perímetro mojado; y A = área de flujo. El factor de forma γ varía en el rango de 0-1. El valor
la derivada es: dP/dA = d1 (P/A) = d1/R.
En la Ecuación 18, para
Con la Ecuación 8, la Ec. 16 se reduce a (Chow 1959):
lo que implica que el número de Vedernikov es una función del número de Froude, afirmación que estrictamente no es correcta. El examen de las ecuaciones. 8 a 10 revela que los números de Froude y Vedernikov son totalmente independientes entre sí. La confusión surge solo circunstancialmente porque la celeridad relativa de la onda cinemática v se expresa en términos de la velocidad media u (Ec. 6).
Dada la Ecuación 10, se concluye lo siguiente:
Establece que β contiene información tanto de la fricción (x) como de la forma de la sección transversal (γ). La Tabla 2 resume las relaciones entre b, x, γ, d1 y β para una amplia gama de condiciones de flujo.
[Ec. 17] [Ec. 17] [Ec. 18] [Ec. 19] [Ec. 21] [Ec. 4]
Subsiste la pregunta de por qué Chow colocó el número de Vedernikov en el Capítulo 8 de su libro, como la última sección [Sección 8-8] del capítulo titulado "Conceptos teóricos..." en lugar de ubicarlo en el Capítulo 1, junto con el número de Froude y otros conceptos fundamentales.
7. CONCLUSIONES
Se revisan los conceptos de los números de Froude y Vedernikov con motivo del 50avo aniversario de la publicación del Manual de Hidrología Aplicada de Ven Te Chow. Mientras que el número de Froude (F) es estándar en la práctica de la ingeniería hidráulica, el número de Vedernikov (V) sigue sin ser reconocido por una gran cantidad de ingenieros en la práctica. Aquí se especula que esto puede deberse en parte al hecho de que Chow colocó el número de Vedernikov en el Capítulo 8 de su libro, en lugar de colocarlo en el Capítulo 1, junto con el número de Froude.
Se lleva a cabo
una descripción completa de la variación de β, el importante exponente de la curva de gasto caudal-área (β - 1 = V/F), para reconocer y honrar las contribuciones del profesor Ven Te Chow a la profesión de ingeniería hidráulica.
AGRADECIMIENTOS
El autor agradece a Aleksandr Gostomelsky, graduado en 2014 del programa de maestría en ingeniería civil de la Universidad Estatal de San Diego, California, quien buscó y finalmente encontró la fotografía del Prof. V. V. Vedernikov que hemos publicado en este artículo, junto con las de Ven Te Chow y William Froude.
BIBLIOGRAFÍA
Ackermann, W. C. 1984. Ven Te Chow, 1919-1981.
Memorial Tributes: National Academy of Engineering, Vol. 2.
Brater, E. F., y H. W. King. 1976. Handbook of Hydraulics. 6th Edition, McGraw-Hill, New York.
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, New York.
Craya, A. 1952. The criterion for the possibility of roll-wave formation. Gravity Waves,
Circular 521, National Bureau of Standards, Washington, D.C., pages 141-151.
Liggett, J. A. 1975. Stability. Chapter 6 in
Unsteady flow in open channels, Vol. 1, K. Mahmood and V. Yevjevich, editors, Water Resources Publications, pages 259-281.
Lighthill, M. J., y G. B. Whitham. 1955.
On kinematic waves: I. Flood movement in long rivers.
Proceedings of the Royal Society, Vol. 29, A, No. HY12, pages 281-316.
Ponce, V. M., y D. B. Simons. 1977.
Shallow wave propagation in open channel flow.
Journal of Hydraulic Engineering, ASCE, Vol. 103, No. HY12, pages 1461-1476, December.
Ponce, V. M. 1989. Engineering Hydrology: Principles and Practices. Prentice Hall, Englewood Cliffs, New Jersey.
Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, pages 1777-1779, July.
Ponce, V. M. 1992.
Kinematic wave modelling: Where do we go from here?
International Symposium on Hydrology of Mountainous Areas, Shimla, India,
May 28-30, pages 485-495.
Ponce, V. M., y P. J. Porras. 1993. Effect of cross-sectional shape on free-surface instability.
Journal of Hydraulic Engineering, ASCE, Vol. 121, No. 4. pages 376-380, April.
Ponce, V. M. 2003.
That's the one we skip! Legacy Tales, link 970 in ponce.sdsu.edu.
Powell, R. W. 1948.
Vedernikov's criterion for ultra-rapid flow.
Transactions, American Geophysical Union, Vol. 29, No. 6, 882-886.
Seddon, J. A. 1900.
River hydraulics. Transactions, ASCE, Vol. XLIII, pages 179-243, June.
Vedernikov, V. V. 1945. Conditions at the front
of a translation wave disturbing a steady motion of a real fluid.
Comptes Rendus (Doklady) de l' Académie des Sciences de l' U.R.S.S., Vol. 48, No. 4. pages 239-242.
Vedernikov, V. V. 1946. Characteristic features of a liquid flow in an open channel.
Comptes Rendus (Doklady) de l' Académie des Sciences de l' U.R.S.S., Vol. 52, No. 3, pages 207-210.
1
Este artículo fue presentado en el Congreso Mundial de Medio Ambiente y Recursos Hídricos de la EWRI ASCE que se llevó a cabo del 1 al 5 de junio de 2014 en Portland, Oregón. Las Sesiones Conmemorativas de Chow, tres en total, fueron organizadas por el Dr. Arie Ben Zvi, exalumno del Prof. Ven Te Chow, para reconocer sus contribuciones a la profesión de ingeniería hidráulica e hidrológica, en el 50avo aniversario de la publicación de su libro Manual de Hidrología Aplicada.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 230511 |