The overriding objective of surface-runoff mathematical modeling is to accurately describe the relevant physical processes of convection and diffusion. Convection, a first-order process, is akin to the movement of the parcels of water in a direction parallel to the underlying terrain. Diffusion, a second-order process, describes the movement of the parcels in a direction perpendicular to the terrain. The combination of these two processes transforms a hyetograph, a histogram of effective rainfall, defined in terms of a series of depths (cm) and an interval duration (hr), into a hydrograph. The latter is a plot of the variation of discharge in time, with clearly defined characteristics such as peak discharge and time-to-peak. Being of first order, convection is the primary, or greater process; diffusion, the second-order process, is normally small and often negligible. In certain cases, however, diffusion may become significant enough to actually affect or interfere with the amount of convection. The accurate determination of the diffusion component is at the crux of surface-runoff modeling, constituting the central topic of this article.

Runoff diffusion is the component of surface runoff that is produced by diffusion. The amount of diffusion was first quantified by Hayami (1951), who combined the governing equations of water continuity and motion, i.e., the Saint-Venant equations (Saint Venant, 1849; Ponce, 2014b: Governing), into a second-order partial differential equation with discharge as the dependent variable. Hayami expressed the diffusion coefficient ν, or Hayami's diffusivity, as follows:

qo ν  =  _______            2So

(1)

in which q_o = unit-width discharge, and S_o = bottom slope. It is seen that runoff diffusion is directly proportional to the unit-width discharge and inversely proportional to the prevailing bottom slope.

The unit-width discharge q_o varies within a narrow range, typically less than two orders of magnitude (10-40 m²/s, or alternatively 1-100 m²/s) (Ponce and others, 2003). However, the bottom slope S_o varies within a much broader range, typically from steeper than 0.1 to milder than 0.00001, i.e., at least five orders of magnitude (Ponce, 1995). Therefore, the bottom slope is seen to be the controlling factor in assessing the amount of runoff diffusion. For bottom slopes greater than 0.01, diffusion is negligible, and an unsteady flow feature may be construed as a kinematic wave, featuring only convection. On the other hand, for bottom slopes smaller than 0.001, diffusion may be substantial, and the unsteady flow feature is essentially diffusive, properly a diffusion wave (Ponce, 2023a). Eventually, as the bottom slope approaches zero, i.e., in the presence of flat land, diffusion tends to infinity, resulting in ponding, with the total absence of surface runoff. At that point, surface-water evaporation takes over.

3.  UNIT HYDROGRAPH THEORY

The rational method has no effective way of accounting for runoff diffusion. As basins increase in surface area from small (A < 2.5 km²) to midsize (2.5 ≤ A < 1,000 km²), runoff diffusion becomes increasingly important and, therefore, a more precise calculation may be required. The larger the basin area, the more likely it is that the mean terrain slope will be milder, although in certain unusual cases this may not be necessarily so. In general, the larger the basin, the greater the amount of runoff diffusion; conversely, the smaller the basin, the smaller the amount of runoff diffusion.

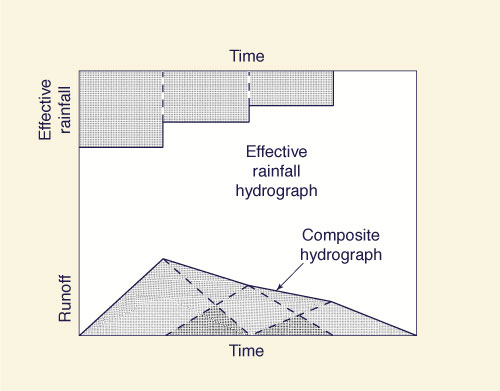
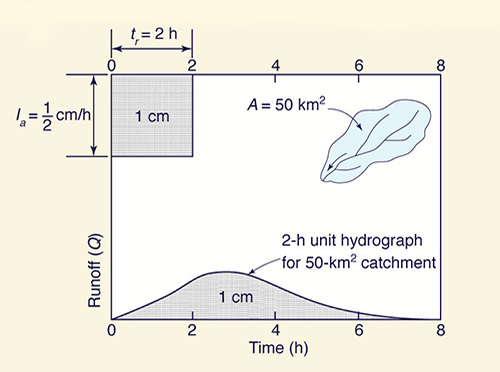
To develop a way to account for runoff diffusion, Sherman (1932) envisioned that he would typify the runoff diffusion of a given basin in terms of a unit hydrograph, defined as the hydrograph corresponding to a unit depth of runoff (1 cm or 1 in) lasting "a unit increment" of time [Fig. 2 (a)]. In Sherman's concept of unit hydrograph, the word unit was meant to refer not to the "unit depth" of runoff, but rather to the fact that the unit runoff was indivisible. Thus, a basin could have several 1-cm unit hydrographs, for instance: (a) the 1.0-cm/hr 1-hr unit hydrograph, (b) the 0.5-cm/hr 2-hr, (c) the 0.25-cm/hr 4-hr, and so on, all of these hydrographs representing 1 cm of runoff. [In essence, once the unit hydrograph duration is chosen, it may not be split]. After one of these unit hydrographs is identified either through field measurement or by a synthetic calculation, the others may be determined based on the first one (Ponce, 2014a: Change in UH Duration).

[Click on top of figure to expand] Fig. 2 (a)  The unit hydrograph.

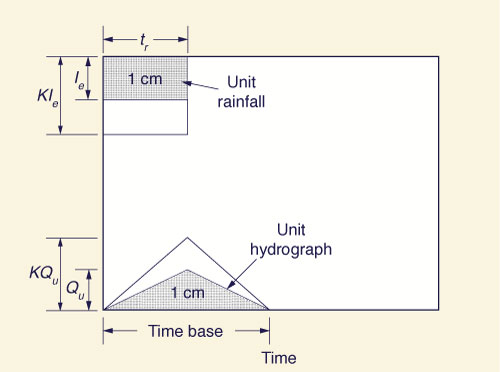
[Click on top of figure to expand] Fig. 2 (b)  The unit hydrograph: Linearity.

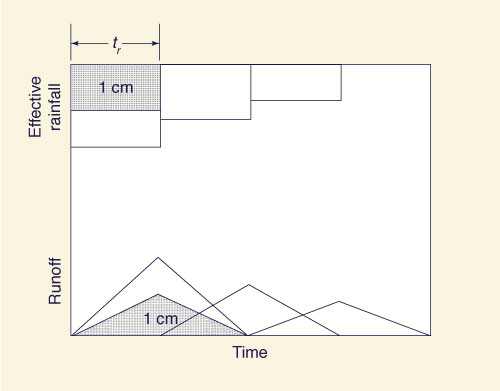
Once the unit hydrograph had been determined for a given basin, Sherman proceeded to apply the convolution technique to calculate the composite flood hydrograph for the corresponding effective rainfall hyetograph (the effective storm pattern). The procedure hinges on an assumption of linearity, that is, given a multiplier K, the hydrograph response to rainfall amount KI_e is taken as KQ_e, in which Q_e = unit hydrograph peak [Fig. 2 (b)]. Given the effective storm hyetograph, the lagging in time of the several hydrograph increments [Fig. 2 (c)] results in the composite flood hydrograph [Fig. 2 (d)] (Ponce, 2014a: Composite).

[Click on top of figure to expand] Fig. 2 (c)  The unit hydrograph: Lagging.

[Click on top of figure to expand] Fig. 2 (d)  The unit hydrograph: Superposition.

The unit hydrograph methodology has been used in hydrologic design for nearly 100 years. It has proven to be a reliable and reproducible procedure, but the central question still remains: How to determine the unit hydrograph for a given basin? Due to the associated cost, actual measurements of unit hydrographs are very few and far between. The synthetic unit hydrographs of Snyder and NRCS stand out, but they are not without their pitfalls. The peak and shape of the actual unit hydrograph [Fig. 1 (a)] depend on the actual amount of runoff diffusion, but both the Snyder and NRCS unit hydrographs feature specific amounts of runoff diffusion. While Snyder's method provides a narrow range of cases, NRCS's method provides only one case, therefore limiting its applicability to basins similar to those used in the method's original development.

What is sorely needed is a methodology to derive a unit hydrograph whose peak and shape are not fixed by a certain amount of runoff diffusion specified by a formula, but one that varies with the actual amount, be it a small or negligible amount in the case of a steep basin, or a large or substantial amount for a mild basin. We will show here that this variability, across the broadest range possible, from zero (0) to infinity (∞) is clearly provided by the method of cascade of linear reservoirs.

4.  CASCADE OF LINEAR RESERVOIRS

The methodology referred to as the cascade of linear reservoirs constitutes an effective way to simulate runoff diffusion in a basin. As its name implies, the method is based on the connection of several linear reservoirs in series, wherein the outflow from the first reservoir is the inflow to the second, the outflow from the second is the inflow to the third, and so on. Each reservoir in the series provides a finite amount of diffusion, with the outflow from the last reservoir reflecting the cumulative diffusion effect of all the reservoirs in the series.

Since the flow is being routed only through reservoirs, it does not provide convection, i.e., runoff concentration (the first-order process). However, the accumulated experience with the method has convincingly shown that appreciable amounts of diffusion may readily be used to model both convection and diffusion. We note that its original use, in connection with the SSARR model, used the procedure to route flow through channels, reservoirs, and basins (U.S. Army Corps of Engineers, 1975). Thus, its flexibility to model any amount of runoff diffusion, in any situation, is amply demonstrated by experience.

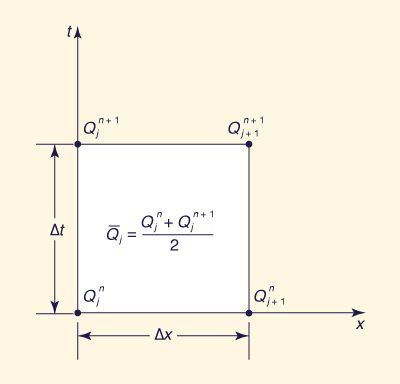
To derive the routing equation for the cascade of linear reservoirs, the point of start is the four-point scheme (Ponce, 2014a: Cascade):

Q j+1 n+1 = C0 Q j n+1 + C1 Q j n + C2 Q j+1 n

(2)

in which Q represents discharge, whether inflow or outflow, and j and n are spatial and temporal indices respectively (Fig. 3).

Fig. 3  Space-time discretization in the method of cascade of linear reservoirs.

The routing coefficients C₀, C₁ and C₂ are a function of the dimensionless ratio referred to as the Courant number C = Δt /K, in which K = linear reservoir storage constant. In terms of the Courant number, the routing coefficients are expressed as follows:

C C0  =  _______             2 + C

(3a)

C1  =  C0

(3b)

2 - C C2  =  _______             2 + C

(3c)

For basin routing, it is convenient to define the average inflow as follows (Fig. 3):

Q j n  +  Q j n+1 Q̄ j = __________________                       2

(4)

Substituting Eqs. 3 and Eq. 4 into Eq. 2 gives the following:

Q j+1n+1 = 2 C1 Q̄ j  +  C2 Q j+1n

(5)

Equation 5 constitutes the routing equation of the cascade of linear reservoirs. Alternatively, through some algebraic manipulation, the following equivalent form is obtained:

2 C Q j+1n+1 =   ________ [ Q̄ j  -  Q j+1n ]  +  Q j+1n                      2 + C

(6)

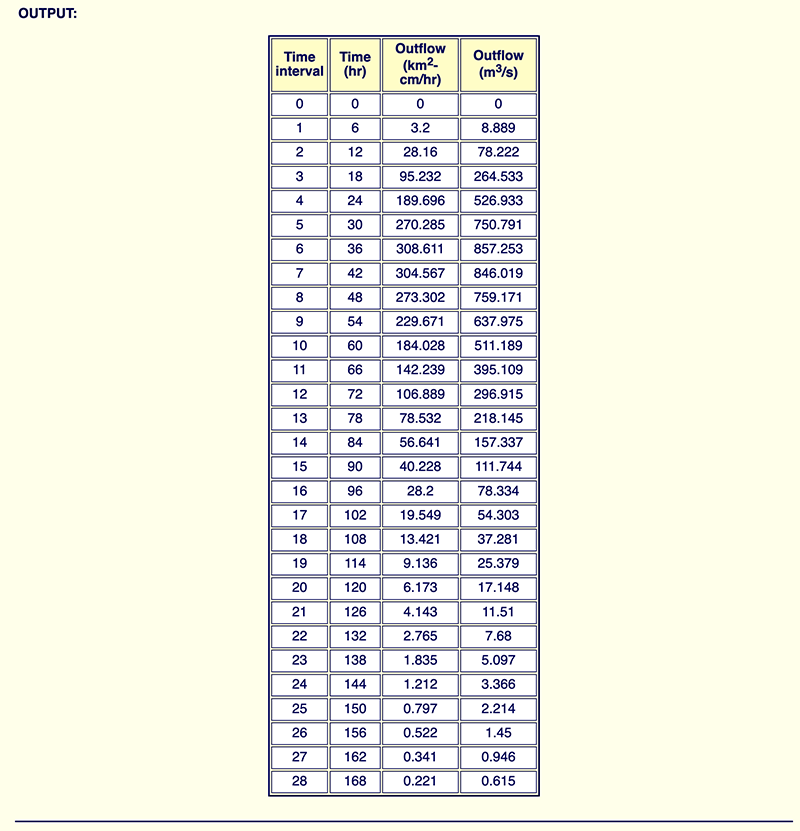
Equation 6 is the routing equation of the SSARR model (U.S. Army Corps of Engineers, 1975). Equations 5 and 6 are in a form convenient for basin routing because the inflow is usually a rainfall hyetograph, that is, a constant average value per time interval. An example of a calculation by the cascade of linear reservoirs (Example 10-3) in given in Ponce (2014a): Example 10-3.

Figure 4 shows an example of the method of the cascade of linear reservoirs using the online script ONLINEROUTING08. The example reproduces the manual calculation shown in Ponce (2014a): Example 10-3, confirming the results.

[Click on top of figure to expand] Fig. 4 (a)  ONLINEROUTING08: Input Data.

[Click on top of figure to expand] Fig. 4 (b)  ONLINEROUTING08: Input/Output.

---

5.  ANALYSIS OF THE CASCADE

The cascade of linear reservoirs (for short, CLR) calculates either: (a) a unit hydrograph, or (b) a flood hydrograph, given the following data: (1) basin area A, (2) reservoir storage constant K, (3) number of reservoirs N, (4) time interval Δt, (5) number m of increments of effective rainfall intensity, and (6) m increments i_e of effective rainfall intensity. The Courant number is defined as: C = Δt /K. Effectively, the method's two parameters are C and N.

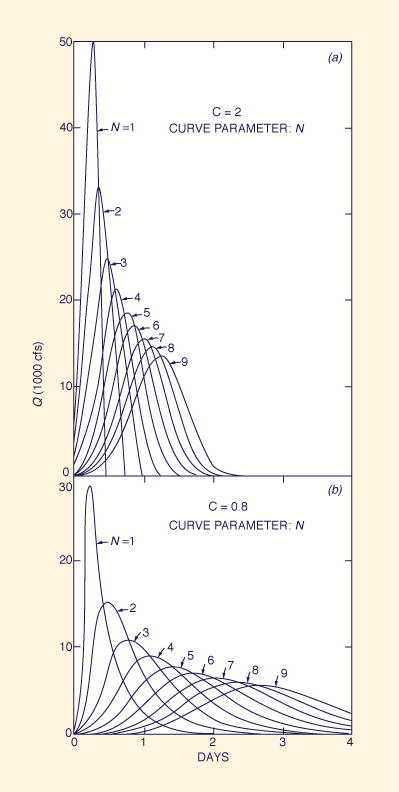
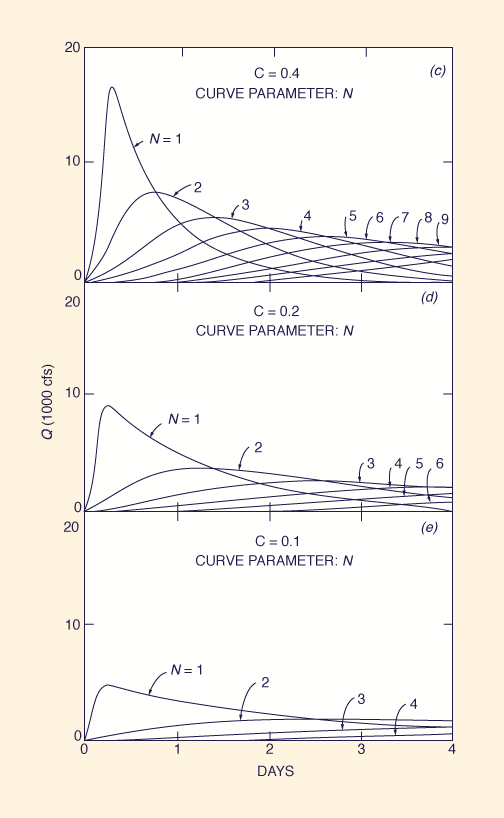
The sensitivity of the method's response to the choice of parameters is demonstrated by the example shown in Box A (Ponce, 1980). This example calculates a 6-hr unit hydrograph (1 inch of runoff) for each C-N pair of a set of five (5) Courant numbers C and nine (9) N values, for a total of forty-five (45) C-N pairs and corresponding unit hydrographs [actually, due to the great amount of diffusion, only six (6) curves can be shown in Fig. 5 (d) and four (4) in Fig. 5 (e)].

Box A.  Data for Example Problem. Basin area A = 465 square miles. Reservoir storage constant K corresponding to the following five Courant numbers (C = Δt /K): C = 2.0, 0.8, 0.4, 0.2, and 0.1. Nine values of N: 1, 2, 3, 4, 5, 6, 7, 8, and 9. Time interval Δt = 6 hr. Number m of increments of effective rainfall intensity: m = 1 (i.e., a unit hydrograph). One increment of effective rainfall intensity i = 1 in / 6 hr = 0.1666667 in/hr.

The results are shown in Fig. 5. The maximum possible peak flow is shown to be: Q_p = 50,000 cfs [Fig. 5 (a) and Box B]. Figure 5 shows that the method is able to simulate a wide range of runoff diffusion effects, from (a) zero diffusion, i.e., Q_p = 50,000 cfs, and time base (of the unit hydrograph) T_b = 12 hr, for C = 2 and N = 1 [Fig. 5 (a)]; to (b) a substantial amount of diffusion, i.e., Q_p < 1,000 cfs for C = 0.1 and N > 4 [Fig. 5 (e)].

[Click on top of figure to expand] Fig. 5 (a)  CLR hydrograph response: (a) C = 2; (b) C = 0.8.

[Click on top of figure to expand] Fig. 5 (b)  CLR hydrograph response: (c) C = 0.4; (d) C = 0.2; (e) C = 0.1.

Box B.  Calculation of the maximum peak flow Qp for Example Problem.                          0.1666667 in/hr × 465 mi2 × (5,280 ft/mi)2 Qp  =  i A  =  ____________________________________________  =  50,013 ≃ 50,000 cfs                                          3,600 s/hr × 12 in/ft

Significantly, the zero diffusion provided by the cascade for the case of C = 2 and N = 1 results in a triangular hydrograph, resembling that of the rational method. For any other C-N pair, diffusion increases with a decrease in Courant number and an increase in the number of reservoirs, as predicted by the theory. For C < 0.1 and N > 9, greater amounts of runoff diffusion than those shown in Fig. 5 (e) are in order, confirming the theoretically infinite amount of diffusion that the method is able to provide. In fact, the diffusion will range from a value of zero (0) applicable for C = 2 and N = 1, to a value approaching infinity (∞) for C = a positive real number very close to zero, and N = a very large integer exceeding 9.

It should be pointed out that since C = 2 is the condition of zero diffusion, then C > 2 produces negative diffusion, that is, hydrograph amplification. In practice, diffusion requires that Δt < 2 K, i.e., the spatial interval must be smaller than twice the reservoir routing constant. Therefore, C = 2 is effectively a practical upper limit for the Courant number.

With the capability of the method of cascade of linear reservoirs amply demonstrated for generating not only unit hydrographs (in this Section) but also composite flood hydrographs (in Section 4), all that remains is the estimation or assessment of the method's two routing parameters applicable to a given problem: (1) the Courant number C, and (2) the number of reservoirs N. This objective may be accomplished in one of the following ways: (a) by calibration, using measured field data; or (b) by estimation, using a variety of synthetic means. The following section (Section 6) elaborates on the geomorphological approach to parameter estimation.

---

6.  CASCADE AND GEOMORPHOLOGY

Hayami's expression for the coefficient of hydraulic diffusivity, Eq. 1, characterizes the behavior of runoff diffusion in basin/watershed free-surface flow. Equation 1 reveals that diffusion is largely controlled by the mean land surface slope. In practice, runoff diffusion manifests itself as the attenuation of the unsteady flow features, i.e., waves and other disturbances. The greater the mean land surface slope, the lesser the amount of diffusion, the latter vanishing for sufficiently large slopes. By definition, kinematic slopes, which are generally greater than 0.01 (1%), have no diffusion. Thus, mountainous terrain is essentially diffusion-free [Fig. 6 (a)] (Ponce, 2023b).

On the other side of the mean land surface slope range, for the extremely mild values, runoff diffusion is very substantial. As mean land surface slope attains the value of zero (i.e., a horizontal plane) diffusion becomes infinite (∞). In this case, all waves and disturburbances diffuse almost instantaneously, and the result is a pond or lake, arresting surface flow [Fig. 6 (b)].

[Click on top of figure to expand] Fig. 6 (a)  The Moyan watershed, headwaters of the La Leche river, Lambayeque, Peru (average terrain slope ≃ 0.3) (Ponce, 2008).

[Click on top of figure to expand] Fig. 6 (b)  The Upper Paraguay river near Porto Murtinho, Mato Grosso do Sul, Brazil (average terrain slope ≃ 0.000008) (Ponce, 1995).

These observations clearly point to terrain geomorphology as the leading factor in assessing runoff diffusion and, consequently, in determining the shape of the unit hydrograph and the related composite flood hydrograph.

Table 1 shows a tentative classification of mean land surface slope, ranging from very steep (S_o > 0.1), to extremely mild (S_o < 0.00001). The applicable cascade parameters have been estimated by Ponce (2009b). The peak flow Q_*p and time-to-peak t_*p of the generalized dimensionless unit hydrograph (GDUH) have been calculated by Ponce (2009a). Note that Q_*p varies from 1 (100% of its value, kinematic flow) for the very steep class, to 0.014 (1.4% of its value, diffusion flow) for the extremely mild class. Likewise, t_*p varies from 1 (1 time interval, kinematic flow) for the very steep class, to 81 (81 time intervals, diffusion flow) for the extremely mild class.

Table 1.  Basin classification for runoff diffusion based on mean land surface slope.
Class	Mean land surface slope So	Cascade parameters		GDUH peak values and time-to-peak
		C	N	Q*p	t*p
Very steep	> 0.1	2	1	1	1
Steep	0.01 - 0.1	1.5	2	0.472	2
Average	0.001 - 0.01	1	4	0.224	4
Mild	0.0001 - 0.001	0.5	6	0.088	11
Very mild	0.00001 - 0.0001	0.2	8	0.03	36
Extremely mild	< 0.00001	0.1	9	0.014	81

In Nature, runoff diffusion acts to obliterate the flood peaks, generally leading to milder peaks and consequently greater low flows. In extremely mild terrain geomorphology, the great amounts of diffusion lead to the occurrence of only one flood peak per year. This is the case of the Pantanal of Mato Grosso, in Brazil, where the extremely mild land slopes, close to S_o = 0.00001 (1 cm/km), result in only one flood peak per year in the lower basin, with its normal occurrence in May or June (Fig. 7). This fact confirms that terrain geomorphology exerts a major influence on the shape and timing of unsteady surface-water flow features.

Fig. 7  The Upper Paraguay river near Porto Murtinho, Mato Grosso do Sul, Brazil, featuring only one flood peak per year due to extreme runoff diffusion.

---

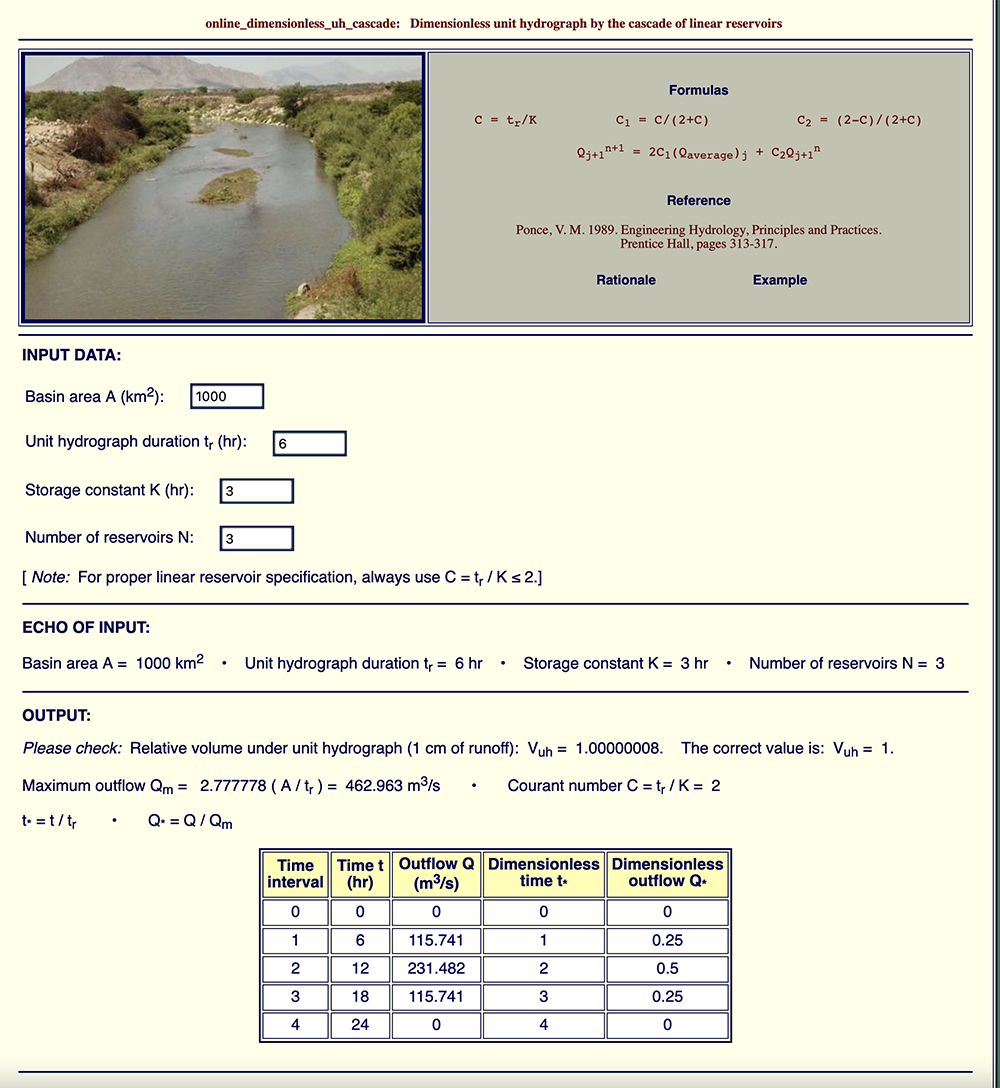
7.  ONLINE EXAMPLES

This section shows several examples of unit hydrographs calculated by the cascade of linear reservoirs using the online scripts developed by Ponce (2009a).

---

Example 1:  ONLINE_DIMENSIONLESS_UH_CASCADE

[Click on top of above link and enter the appropriate data to run online script]

[https://ponce.sdsu.edu/onlinedimensionlessuhcascade.php]

Example 1A, shown in Fig. 8 (a), calculates actual and dimensionless unit hydrographs for the following input data: (1) Basin area A = 1,000 km²; (2) Courant number C = 2; and (3) number of reservoirs N = 3. The calculated peak outflow is Q_p = 231.482 m³/s, occurring at t = 12 hr. The dimensionless unit hydrograph peak outflow is Q_*p = 0.5, occurring at t_*p = 2.

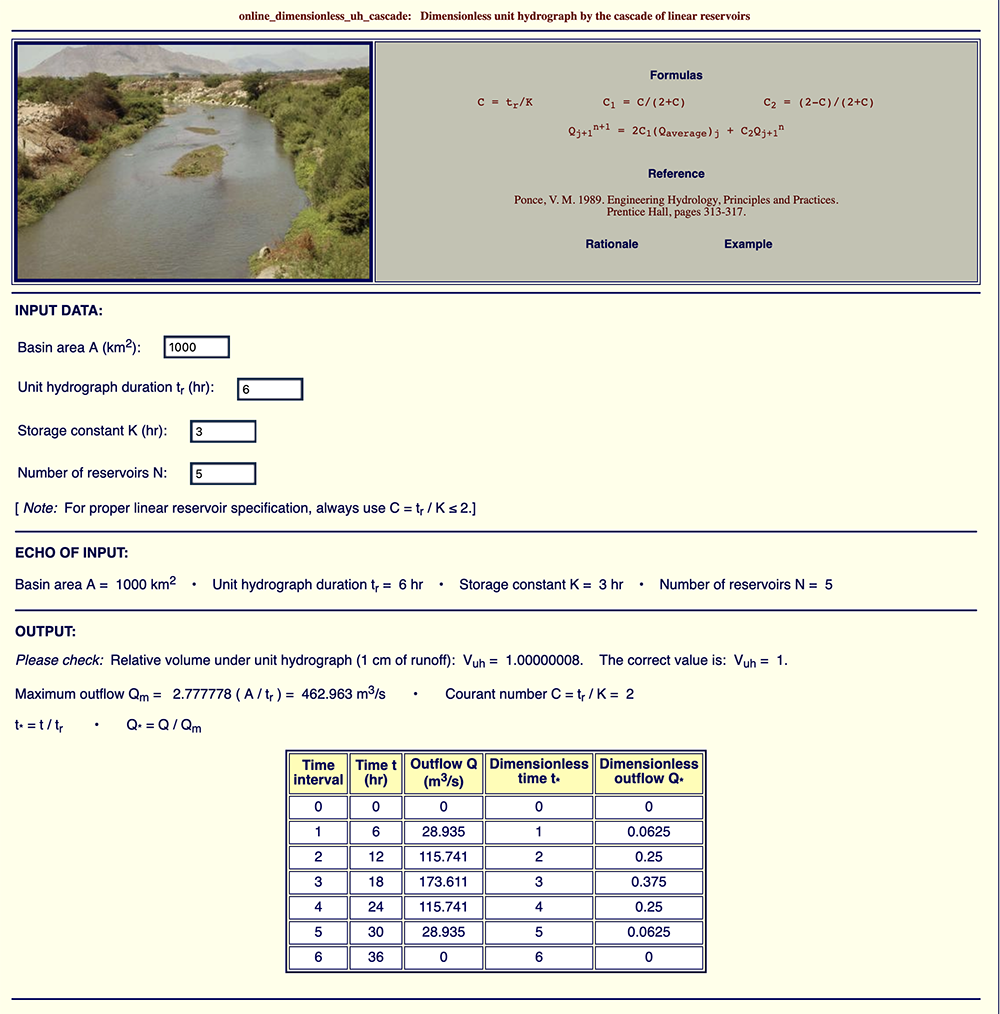
Example 1B, shown in Fig. 8 (b), uses the same basin area A and Courant number C as Example 1A, but increases the number of reservoirs to N = 5. The calculated peak outflow is Q_p = 173.611 m³/s, occurring at t = 18 hr. The dimensionless unit hydrograph peak outflow is Q_*p = 0.375, occurring at t_*p = 3.

Examples 1A and 1B show that increasing the number of reservoirs from 3 (Example 1A) to 5 (Example 1B) has decreased (i.e., attenuated, diffused) the unit hydrograph peak outflow Q_p from 231.482 to 173.611 m³/s, while increasing the time-to-peak t_p from 12 to 18 hr. The dimensionless unit hydrograph peak outflow Q_*p has decreased from 0.5 to 0.375, while the dimensionless time-to-peak t_*p has increased from 2 to 3.

[Click on top of figure to expand] Fig. 8 (a)   Example 1A:  Unit hydrograph for C = 2 and N = 3.

[Click on top of figure to expand] Fig. 8 (b)   Example 1B:  Unit hydrograph for C = 2 and N = 5.

---

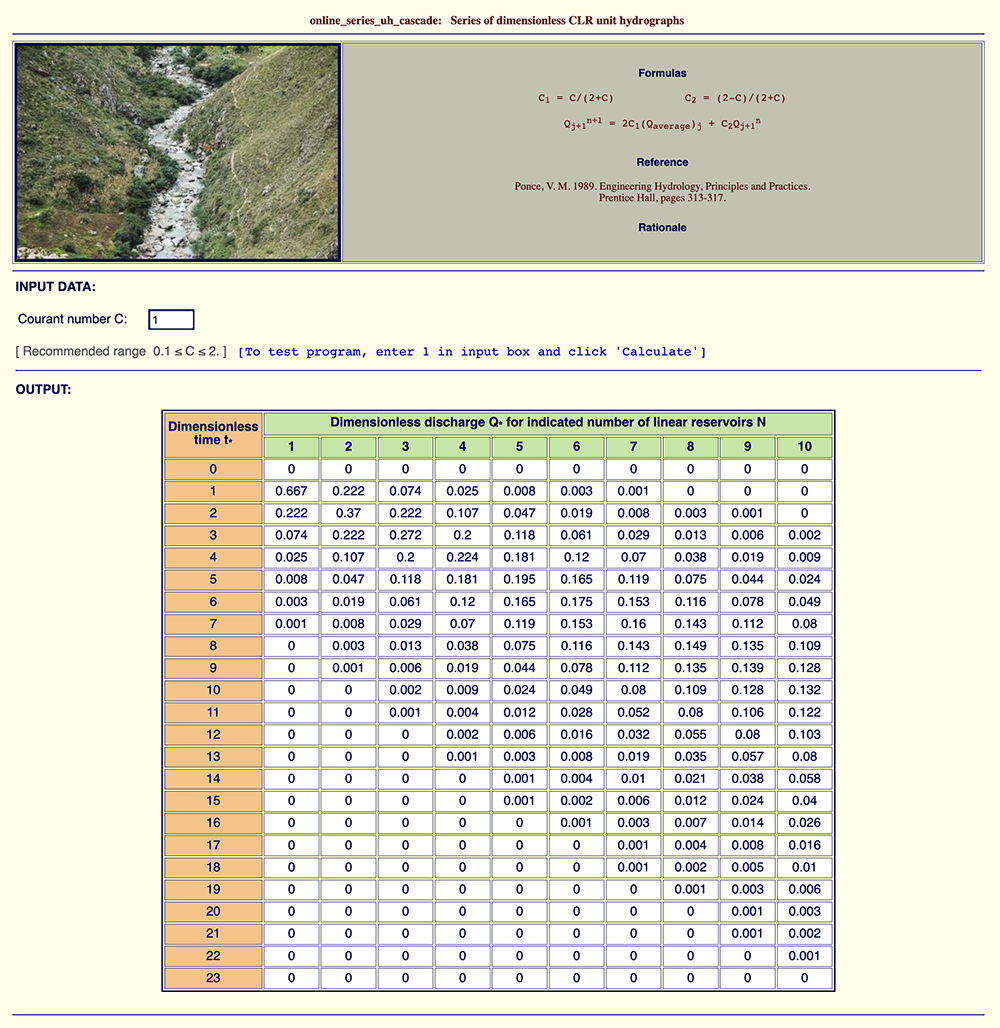
Example 2:  ONLINE_SERIES_UH_CASCADE

[Click on top of above link and enter C = 1 to run online script]

[https://ponce.sdsu.edu/onlineseriesuhcascade.php]

This example shows the calculation of dimensionless unit hydrographs for a given Courant number C and the number of reservoirs in the range 1 ≤ N ≤ 10. For this example, C = 1. The results are shown in Fig. 9. It is seen that diffusion increases with the number of reservoirs. For N = 1, Q_*p = 0.667 at t_*p = 1; for N = 10, Q_*p = 0.132 at t_*p = 10.

[Click on top of figure to expand] Fig. 9   Example 2:  Dimensionless unit hydrographs for C = 1 and 1 ≤ N ≤ 10.

---

Example 3:  ONLINE_ALL_SERIES_UH_CASCADE

[Click on top of above link and then Click "Calculate" to run online script in default mode for the entire specified series]

[https://ponce.sdsu.edu/onlineallseriesuhcascade.php]

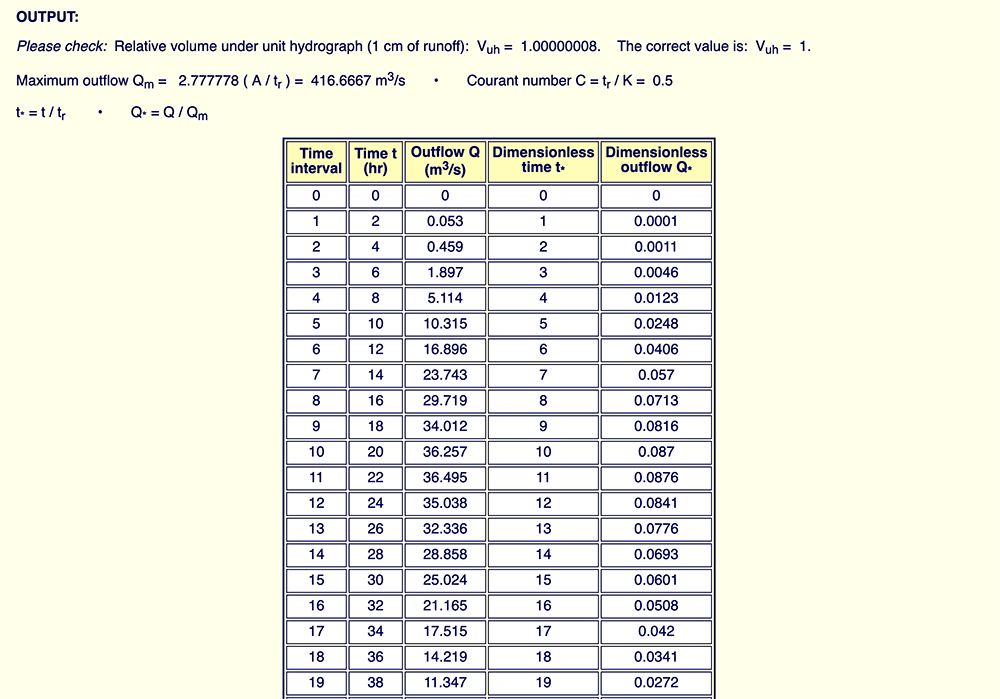
This example shows the calculation of dimensionless unit hydrographs for six (6) Courant numbers in the range 0.1 ≤ C ≤ 2.0 and ten (10) cascades of reservoirs (N = number of reservoirs in each cascade), with 1 ≤ N ≤ 10. The script produces sixty (6 × 10 = 60) dimensionless unit hydrographs, encompassing all combinations of Courant numbers C = 0.1, 0.2, 0.5, 1.0, 1.5, and 2.0, and number of reservoirs N = 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10. As predicted by the theory, it is confirmed that runoff diffusion increases with a decrease in Courant number C and an increase in the number N of reservoirs in the cascade.

---

Example 4:  PRACTICAL APPLICATION

[https://ponce.sdsu.edu/onlinedimensionlessuhcascade.php]

Problem statement. Calculate the t_r = 2-hr unit hydrograph for a basin with surface area A = 300 km² and mean land surface slope S_o = 0.005.

Answer. According to Table 1, this basin is classified as mild. Therefore, the applicable cascade parameters are estimated from this table as C = 0.5 and N = 6. The time interval Δt ≡ t_r = 2 hr, and the reservoir storage constant is: K = Δt / C = 2 / 0.5 = 4 hr.

We run ONLINE_DIMENSIONLESS_UH_CASCADE with A = 300 km², unit hydrograph duration t_r = 2 hr, storage constant K = 4 hr, and number of reservoirs N = 6. Box C shows the calculation of the maximum peak outflow, verified to be Q_p = 416.6667 m³/s. The volume under the unit hydrograph is verified to be 1 cm of runoff (see Fig. 10).

The resulting dimensional and dimensionless unit hydrographs are shown in Fig. 10. The dimensional unit hydrograph peak outflow is Q_p = 36.495 m³/s at the time-to-peak t_p = 22 hr. The dimensionless unit hydrograph peak outflow is Q_*p = 0.0876 at the dimensionless time-to-peak t_*p = 11.

Box C.  Calculation of the maximum peak flow Qp for Example 4.                          0.5 cm/hr × 300 km2 × (1,000 m/km)2 Qp  =  i A  =  _________________________________________  =  416.6667 m3/s                                       3,600 s/hr × 100 cm/m

[Click on top of figure to expand] Fig. 10 (a)   Example 4:  Input Data.

[Click on top of figure to expand] Fig. 10 (b)   Example 4:  Output.

---

8.  SUMMARY

A review of the method of cascade of linear reservoirs for unit hydrograph development is presented, explained, and clarified. Section 1 compares the cascade with the synthetic unit hydrographs of Snyder and NRCS. Section 2 presents basin modeling concepts, including Hayami's diffusivity, which characterizes the diffusion of one-dimensional free-surface flows. Section 3 reviews concepts of unit hydrograph theory. Section 4 explains the methodology of cascade of linear reservoirs, deriving the routing equation and displaying actual online example calculations. Section 5 provides an analysis of the cascade, focusing on its capability to model a broad range of runoff diffusion effects, from zero (0) to infinity (∞). Section 6 describes the geomorphological approach to estimate the parameters of the cascade. Section 7 provides several examples of online calculation, including an actual practical application (Example 4).

The cascade of linear reservoirs is predicated on its capability to model a broad range of runoff diffusion effects, enabling increased accuracy for simulating synthetic unit hydrographs and associated flood hydrographs. The online computational capability enhances the method's utility for the effective modeling of runoff diffusion to solve a wide variety of flooding problems.

---

REFERENCES

Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, December.

Natural Resources Conservation Service (NRCS). 1985. National Engineering Handbook. Section 4: Hydrology, Washington, D.C. (First edition: 1954).

Ponce, V. M. 1980. Linear reservoirs and numerical diffusion. Journal of the Hydraulics Division, Vol. 106, No. 5, May, 691-699.

Ponce, V. M. 1991. The kinematic wave controversy. Journal of Hydraulic Engineering, Vol. 117, No. 4, April, 511-525.

Ponce, V. M. 1995. Hydrologic and environmental impact of the Parana-Paraguay waterway on the Pantanal of Mato Grosso, Brazil. https://ponce.sdsu.edu/hydrologic_and_environmental_impact_of_the_parana_paraguay_waterway.html

Ponce, V. M. 2008. La Leche river flood control project, Lambayeque, Peru. https://ponce.sdsu.edu/0908231200.html

Ponce, V. M. 2009a. A general dimensionless unit hydrograph.
https://ponce.sdsu.edu/general_dimensionless_unit_hydrograph.html

Ponce, V. M. 2009b. Cascade and convolution: One and the same.
https://ponce.sdsu.edu/cascade_and_convolution.html

Ponce, V. M., A. Taher-Shamsi and A. V. Shetty. 2003. Dam-breach flood wave propagation using dimensionless parameters. Journal of Hydraulic Engineering, Vol. 129, No. 10, October, 777-782.

Ponce, V. M. 2014a. Engineering Hydrology: Principles and Practices. Online textbook.
https://ponce.sdsu.edu/enghydro/index.html

Ponce, V. M. 2014b. Fundamentals of Open-channel Hydraulics. Online textbook.
https://ponce.sdsu.edu/openchannel/index.html

Ponce, V. M. 2023a. When is the diffusion wave applicable? Online paper.

Ponce, V. M. 2023b. Kinematic and dynamic waves: The definitive statement. Online paper.

Saint-Venant, B. de. 1871. Theorie du mouvement non-permanent des eaux avec application aux crues des rivieres et l' introduction des varees dans leur lit, Competes Rendus Hebdomadaires des Seances de l'Academie des Science, Paris, France, Vol. 73, 1871, 148-154.

Sherman, L. K. 1932. Streamflow from Rainfall by Unit-Graph Method. Engineering News-Record, Vol. 108, April 7, 501-505.

Snyder, F. F. 1938. Synthetic Unit-Graphs. Transactions, American Geophysical Union. Vol. 19, 447-454.

U.S. Army Corps of Engineers. 1975. Program Description and User Manual for SSARR Model, Streamflow Synthesis and Reservoir Regulation. North Pacific Division, Portland, Oregon, September, revised June, 1975.

---