1.  Ondas pulsantes en canales

Figura 1  La foto clásica de Cornish (1907) en un canal en los Alpes Suizos.

Figura 2  Canal de irrigación, Cabana-Mañazo, Puno, Perú (2007).

Video 1  Canal del río Achumani, La Paz, Bolivia (2014).

Video 2  Canal del río Huayñajahuira, La Paz, Bolivia (2016).

2.  Flujo inestable en canales

El número de Vedernikov

Chow, Froude, y Vedernikov (2014)

Q = α A^{1 + (V / F)}

3.  Efecto de la sección transversal

Figura 3  Río Misisipi en Mud Island, Memphis, Tennessee, EE.UU. (2014).

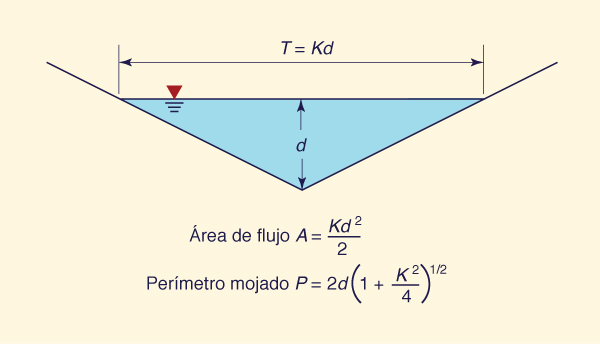
Figura 4  Definición de una sección triangular típica.

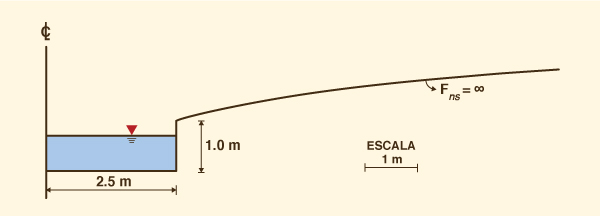
Figura 5  Ejemplo de una sección transversal inherentemente estable.

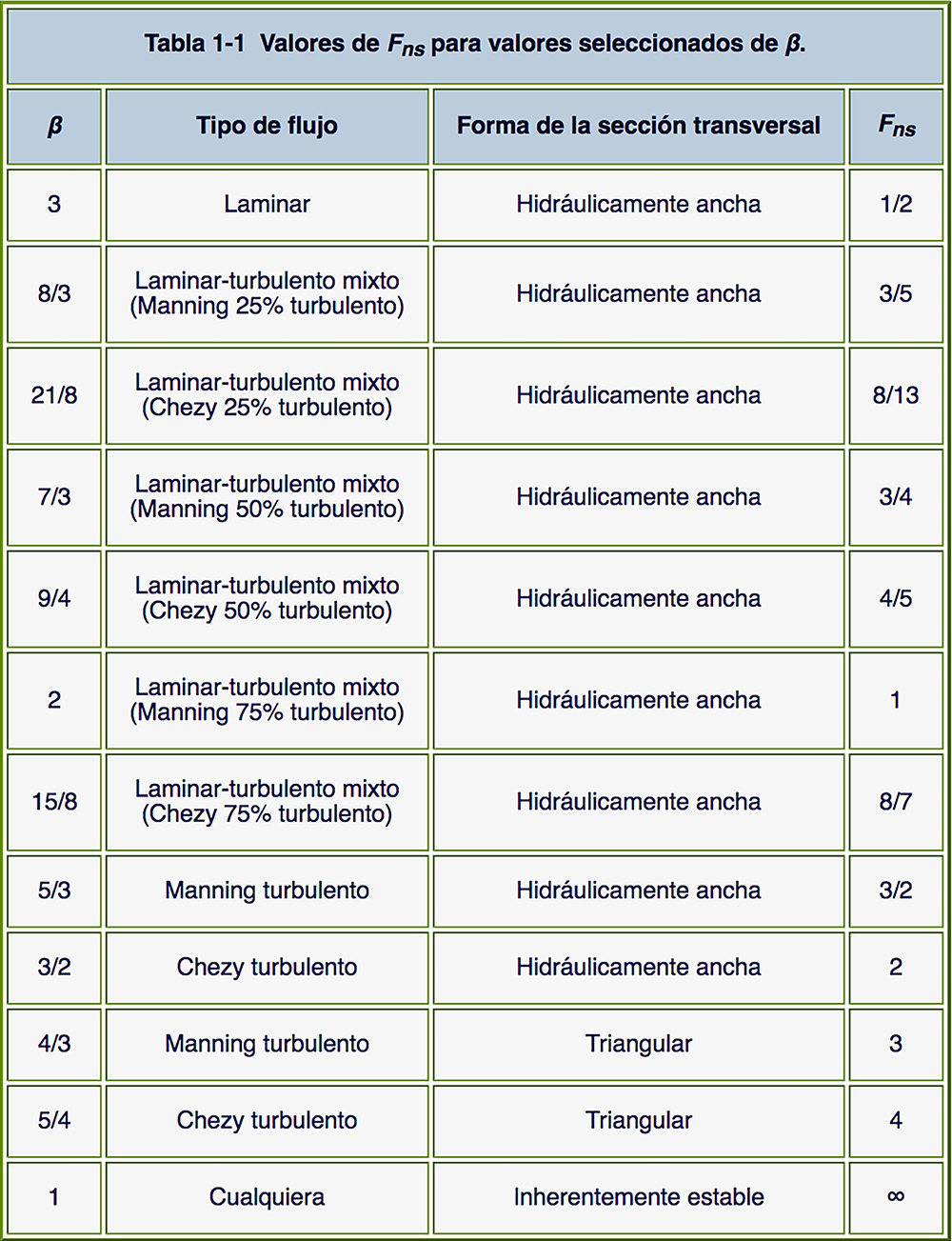
Tabla 1  Valores del número de Froude neutralmente estable para diversos valores
del exponente de la curva de gasto β.

4.  Propagación de ondas en flujo en canales (Ponce y Simons, 1977; Ponce, 2014)

Profundidad de referencia:   d_o

Pendiente media del flujo:   S_o

Longitud de referencia del canal:   L_o = d_o / S_o

Número de onda adimensional:   σ = (2 π / L) L_o

Velocidad media de referencia:   u_o

Celeridad de la onda:   c = β u_o

Celeridad relativa adimensional:   c_r = (c - u_o) / u_o

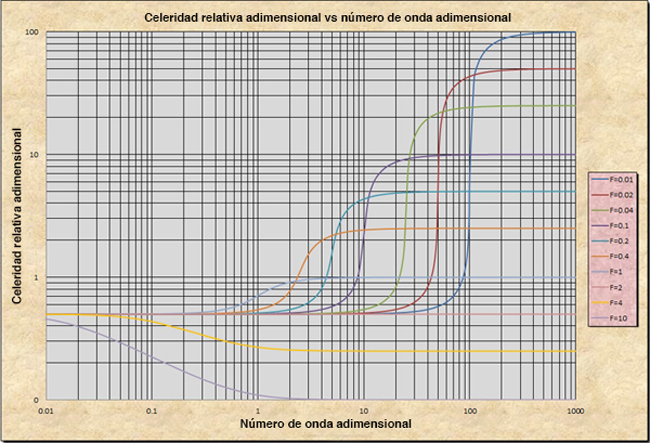
Figura 6  Celeridad relativa adimensional de la onda primaria
en función del número de onda adimensional.

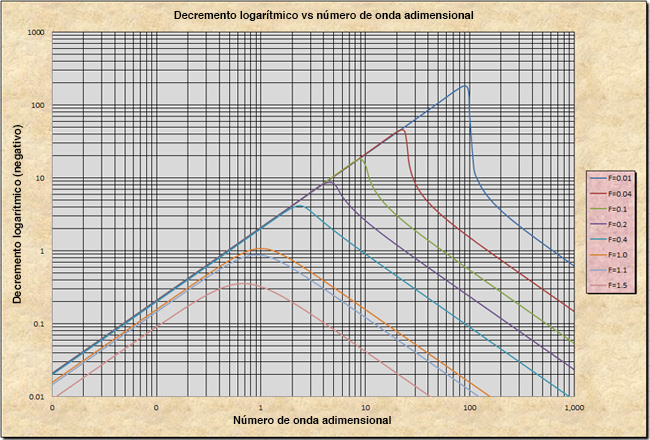
Figura 7  Decremento logarítmico de la onda primaria, para números de Froude F < 2,
equivalentes a números de Vedernikov V < 1.

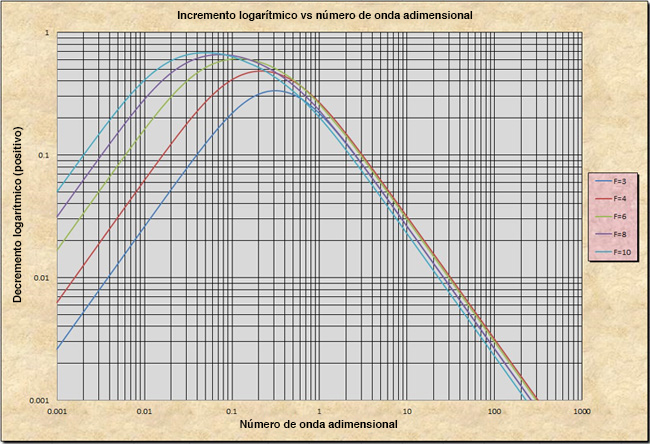
Figura 8   Incremento logarítmico de la onda primaria, para números de Froude F > 2,
equivalentes a números de Vedernikov V > 1.

5.  Verificación de mediciones de ondas pulsantes (Ponce y Maisner, 1993)

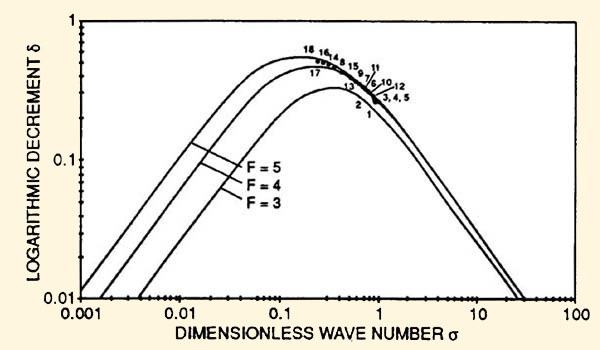
Figura 9 (a)  Incremento logarítmico de la onda primaria en función del número
de onda adimensional, para números de Froude de 3 a 5.

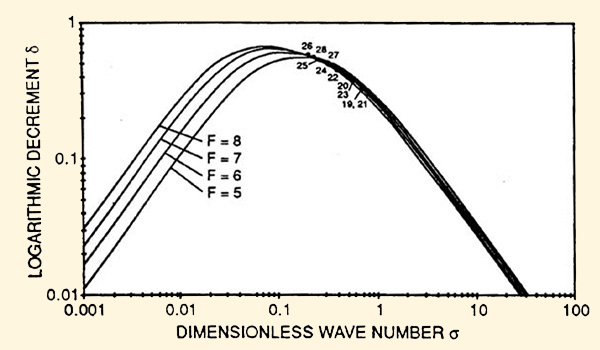
Figura 9 (b)  Incremento logarítmico de la onda primaria en función del número
de onda adimensional, para números de Froude de 5 a 8.

6.  Atenuación mecánica de ondas en canales (Ponce y Windingland, 1985)

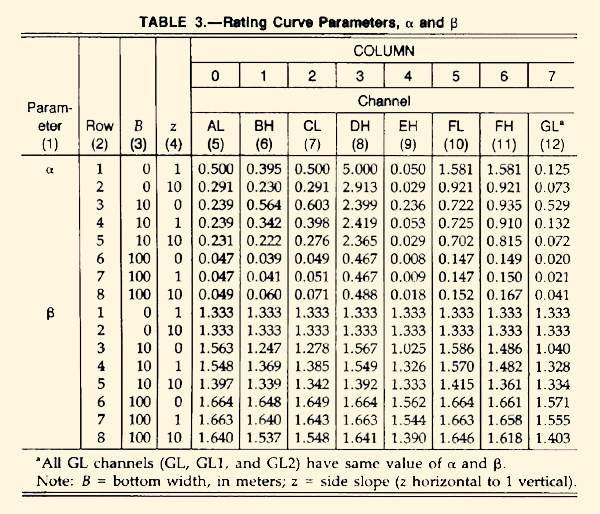
Figura 10 (a)  Tabla que muestra los valores de coeficiente α y exponente β
de la curva de gasto para diferentes tipos de canales y flujos.

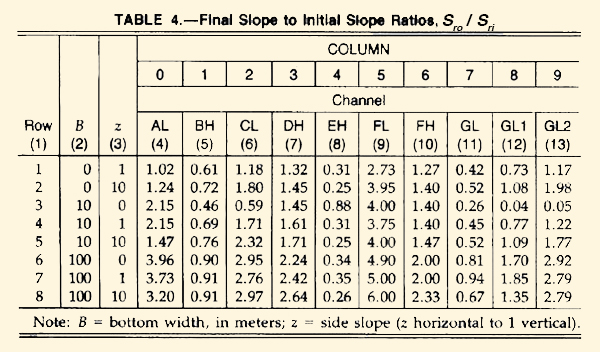
Figura 10 (b)   Tabla que muestra los valores de razones de pendiente S_ro /S_ri
de la superficie del agua (pendiente final a pendiente inicial),
para diferentes tipos de canales y flujos.

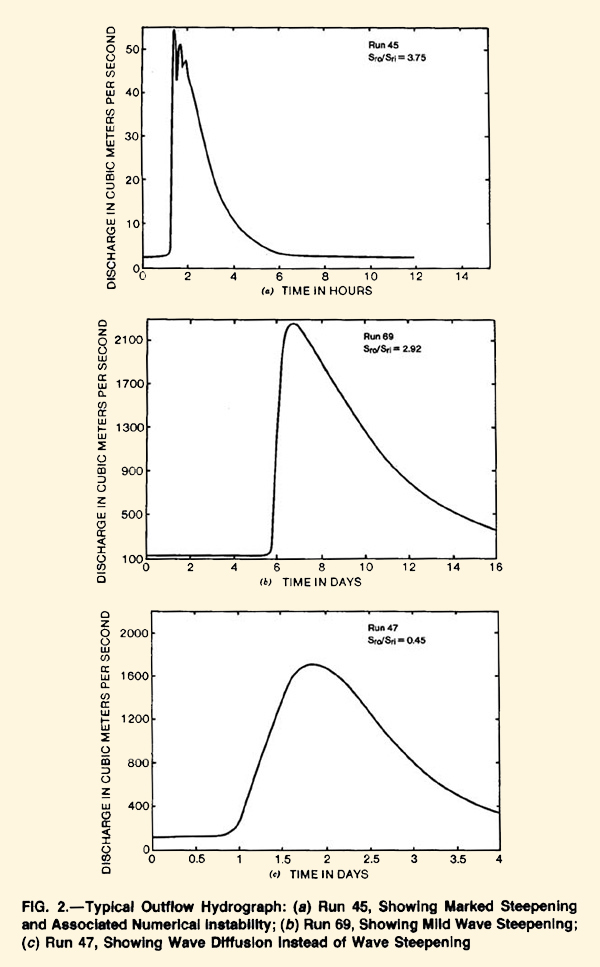
Figura 11   Tres hidrogramas que muestran el efecto del tipo de canal y flujo sobre la cantidad de atenuación de ondas. (a) Corrida 45: Atenuación pequeña; (b) Corrida 69: Atenuación media; y
(c) Corrida 47: Atenuación grande.

7.  Conclusiones

Sección 1 El flujo en canales abiertos con números de Vedernikov V > 1 puede causar el desarrollo de ondas pulsantes (Video 1). Bajo circunstancias desfavorables inusuales, estas ondas pueden ser de tal magnitud que pongan en peligro la vida humana (Video 2). Sección 2 El número de Vedernikov V es la relación entre la celeridad relativa de la onda cinemática (la onda de Seddon) y la celeridad relativa de la onda dinámica (la onda de Lagrange). La condición V ≥ 1 es condición necesaria para la formación de ondas pulsantes, pero no es suficiente. Las ondas pulsantes se producen usualmente bajo condiciones aleatorias favorables en la frontera aguas arriba (el período del hidrograma de entrada). Sección 3 El valor β del exponente de la curva de gasto determina el valor de número de Vedernikov. La forma de la sección transversal determina si el número de Vedernikov alcanza o excede el umbral V = 1. El canal inherentemente estable (Figura 5), con valor β = 1, es decir, equivalente a V = 0, es estable para cualquier valor de flujo, independientemente de las condiciones hidráulicas, permanentes o no permanentes. Sección 4 La propagación de ondas en canales está controlada por el número de onda adimensional σ (Figuras 6 a 8). La amplificación de ondas se produce generalmente para V ≥ 1 en conjunción con valores medios del número de onda adimensional (Figura 8). Sección 5 Para V ≥ 1, la amplificación de ondas es máxima para valores del incremento logarítmico δ cercanos al máximo (Figura 9). Sección 6 La atenuación mecánica de las ondas es minima para valores de β ≅ 3/2 (fricción de Chezy) o β ≅ 5/3 (fricción de Manning) (Figuras 10 y 11). La atenuación es máxima para valores de β → 1, es decir, para V → 0 (Figuras 10 y 11). Los valores de β cercanos a 1 se producen para canales de aspecto profundo, es decir cuando la profundidad de flujo excede substancialmente al ancho del canal. La división, en la entrada, de un canal rectangular normal en varios canales angostos y profundos, cada uno con D2 >> B2, para los cuales β ≅ 1, producirá la atenuación de las ondas, contribuyendo así a controlar la formación de ondas pulsantes en el flujo aguas abajo. Lo anterior equivale al diseño y construcción de un difusor en la entrada del canal, el que contribuirá a atenuar las ondas que puedan desarrollarse aleatoriamente en la vecindad de la frontera aguas arriba.

8.  Aplicación al canal del Río Huayñajahuira, La Paz, Bolivia

I:  Sin difusor

Forma:   Rectangular

Ancho B₁:  5.95 m

Profundidad Y₁:  3.01 m

Pendiente S:  0.056

Coeficiente de Manning (muro de mampostería) n:  0.025

Caudal de diseño (sin borde libre) Q₁:   221.7 m³/s

Velocidad media V₁:  12.38 m/s

Número de Froude F₁:  2.279

II:  Con difusor

Forma:   Rectangular

Ancho B₂:  1.00 m

Profundidad Y₂:  3.01 m

Pendiente S:  0.056

Coeficiente de Manning (muro de mampostería) n:  0.025

Caudal de diseño (sin borde libre) Q₂:  16.20 m³/s

Velocidad media V₂:  5.382 m/s

Número de Froude F₂:  0.99

Número de canales para conducir el caudal de diseño Q₁:  13.69 ≅ 14