¿Es la curva de gasto de sedimentos realmente curva?, Victor M. Ponce

[Haga click encima de la figura para desplegar]

Redibujado del Manual ASCE No. 75, p. 476 (1975)

¿LA CURVA DE GASTO DE SEDIMENTOS ES REALMENTE CURVA?

Victor M. Ponce

Profesor Emérito de Ingeniería Civil y Ambiental

San Diego State University, San Diego, California

07 diciembre 2023

RESUMEN. Se revisa, explica y aclara la naturaleza de una curva de gasto de sedimentos. La "última concentración de sedimentos" es la concentración máxima que se puede alcanzar en ausencia de la fricción del lecho. Su valor puede calcularse directamente en función de las propiedades del flujo y del sedimento. La curva de gasto de sedimentos es una curva, siendo la pendiente alta, alrededor de 7, para los flujos más bajos, y disminuyendo hasta el valor característicamente bajo de 3 para los flujos más altos. Este comportamiento es una consecuencia directa del aumento en la fricción total del lecho. lo cual puede atribuirse a las formas de rugosidad del lecho existentes en el régimen inferior, es decir, dunas y ondulaciones superpuestas. Estas formas interfieren con la capacidad del flujo para transportar la última concentración de sedimentos, reduciendo así la carga de sedimentos. El razonamiento anterior aclara el motivo de la caída en el transporte de sedimentos para flujos bajos y, por lo tanto, explica la forma típica de una curva de gasto de sedimentos. Una verificación con datos de campo confirma los hallazgos de este estudio: Cuanto mayor es la fricción total del lecho, menor es la cantidad de sedimento transportado, y viceversa.

1. INTRODUCCIÓN

La curva de gasto de sedimentos es la relación entre la descarga de agua Q en las abscisas y la descarga de sedimentos Q_s en las ordenadas. La curva es utilizada en la hidráulica fluvial y en la ingeniería de sedimentos para convertir directamente de una descarga a otra, normalmente de Q a Q_s (ASCE, 1975; 2007). En la práctica, la curva se entiende fácilmente por lo que logra; sin embargo, la comprensión de su verdadera naturaleza a menudo pasa desapercibida.

En este artículo detallamos las complejidades de la curva de gasto de sedimentos. Explicamos cómo la Naturaleza ha condicionado los ríos y arroyos aluviales para crear un entorno donde los peces y otras especies continuarían prosperando a pesar de que el clima local no parece cooperar. En este proceso, se unen los campos de climatología, geología, geomorfología, hidrología y ecología en un tejido sin costura, en el cual el principal propósito es la preservación de la biota (Kennedy, 1983). Para preparar el escenario adecuado para explicar los conceptos que seguirán en las siguientes secciones, comenzamos por presentar tres verdades fundamentales de la hidraulica fluvial.

2. TRES VERDADES FUNDAMENTALES DEL TRANSPORTE DE SEDIMENTOS

Verdad No. 1. La relación entre la descarga de sedimentos Q_s y la descarga de agua Q se conoce como concentración de sedimentos C_s (Ec. 1). En condiciones de equilibrio, bajo flujo permanente en una corriente aluvial, la concentración de sedimentos es la carga de sedimentos más alta que la corriente es capaz de transportar bajo el flujo predominante. Esto se debe a que un valor más bajo de C_s conduciría a la degradación del lecho; por el contrario, un valor más alto conduciría a la agradación; y ambas situaciones desafiarían el equilibrio. En la ingeniería de sedimentos, la concentración de sedimento en equilibrio se conoce como "capacidad de transporte de sedimentoss", expresada en unidades F/T, es decir, kilogramos por segundo o toneladas por día. En una corriente aluvial, el flujo permanente siempre transporta la carga máxima de sedimentos que le es posible transportar.

Q_s
C_s = ^_____
Q

(1)

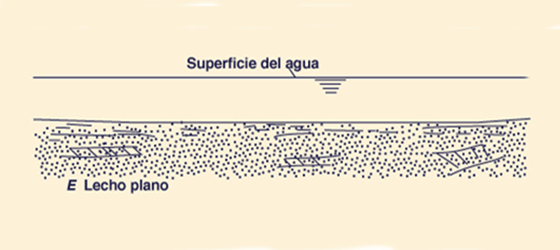
Verdad No. 2. Una corriente aluvial transporta sedimentos que se originan en el lecho, es decir, la carga de material del lecho, de dos maneras distintas: (1) rodando y deslizándose a lo largo del lecho, es decir, la carga del lecho, y (2 ) en suspensión a lo largo de la profundidad, por acción de la turbulencia del flujo sobre las partículas de sedimento que son arrastradas, es decir, la carga de material del lecho en suspensión. Además, una corriente aluvial transporta un tercer tipo de carga, la carga de lavado, consistente en sedimentos de menor tamaño, los cuales no se han originado en el lecho de la corriente, sino en las tierras altas de la cuenca (ASCE, 1975; Ponce, 2014a). La colección de estos tres tipos de carga constituye la carga total de sedimentos (Fig. 1).

Relación entre las dos clasificaciones de carga de sedimentos		Clasificación
		1. Basada en el modo predominante de transporte	2. Basada en si los tamaños de partículas están representados en el lecho
Carga total de sedimentos	Carga de lavado	Carga suspendida	Carga de lavado
	Carga suspendida de material del lecho		Carga de material del lecho
	Carga del lecho	Carga del lecho

Fig. 1 Tipos de carga de sedimento en una corriente aluvial.

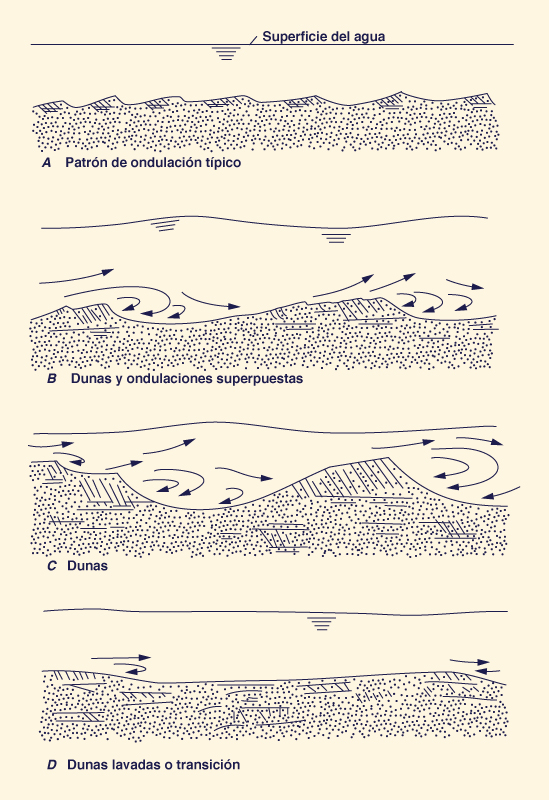
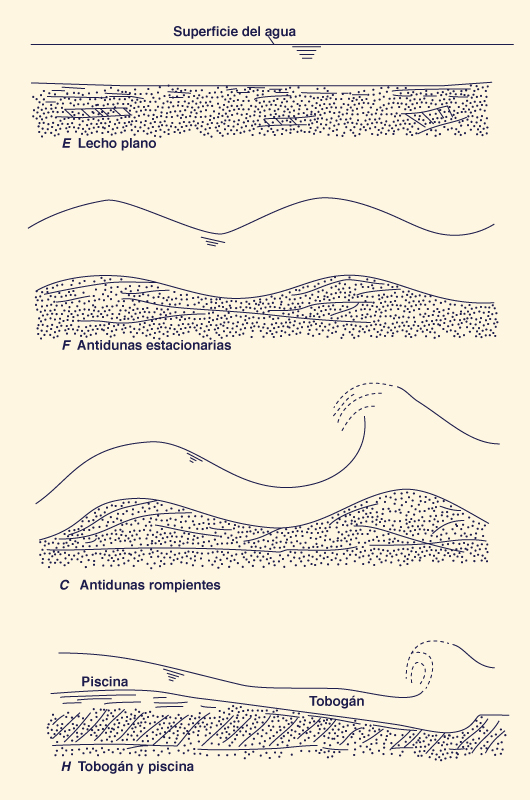
Verdad No. 3. El flujo en un canal aluvial puede está en cualquier uno de dos regímenes: (1) régimen inferior, y (2) régimen superior. Bajo el régimen inferior, el cual tiene lugar para números de Froude bajos, F < 0,5, la carga del lecho genera formas de rugosidad del lecho, específicamente dunas y ondulaciones superpuestas [Fig. 2(a)]. Estas formas actúan para aumentar la fricción total, que ahora consiste en fricción de grano y fricción de forma (Einstein, 1950). Por el contrario, bajo el régimen superior, que tiene lugar para números de Froude más altos, F > 0,5, la rapidez del flujo actúa para borrar las ondulaciones y las dunas, disminuyendo la fricción total a sólo la fricción de grano, lo que lleva a una configuración de lecho plano [Fig. 2 (b)] (Simons y Richardson, 1966).

El cambio de alta fricción para flujos bajos a baja fricción para flujos altos tiene el efecto neto de reducir la fluctuación de la superficie del agua para un cambio correspondiente en el caudal. Por lo tanto, el nivel es más alto de lo normal para flujos bajos y más bajo para flujos altos. Esto redunda en una clara ventaja para la supervivencia de la biota (Kennedy, 1983). Cabe señalar que en el río Alto Paraguay, en Mato Grosso do Sul, Brasil, este inusual fenómeno es conocido como autodragado (Ponce, 1995).

En resumen, las tres verdades fundamentales de la hidráulica fluvial son:

El transporte de sedimentos en flujo de equilibrio occurre a su máxima capacidad. Bajo esta condición, una corriente siempre transportará la máxima cantidad de sedimentos que le sea posible transportar.
La corriente transporta tres tipos de sedimentos: (1) carga de lecho, (2) carga suspendida de material de lecho, y (3) carga de lavado.
La fricción de fondo varía con el regimen de flujo. En flujos bajos, el mismo flujo crea formas de rugosidad del lecho, es decir, dunas y ondulaciones superpuestas. Estas últimas son obliteradas en flujos altos, llevando a superficies planas y otras configuraciones menos rugosas del lecho.

[Haga click encima de la figura para desplegar]

Simons y Richardson (1966)

Fig. 2 (a) Formas de rugosidad del lecho: Régimen bajo.

[Haga click encima de la figura para desplegar]

Simons y Richardson (1966)

Fig. 2 (b) Formas de rugosidad del lecho: Régimen alto.

3. ÚLTIMA CONCENTRACIÓN DE SEDIMENTOS

En la ingeniería práctica se utiliza la siguiente función exponencial para proporcionar un ajuste entre datos medidos de descarga de agua y sedimentos:

Q_s = c Q^m

(2)

en la cual c y m son coeficiente y exponente de la curva de gasto de sedimentos, respectivamente.

En la Ecuación 2, para el caso especial de m = 1, la concentración de sedimentos (Ec. 1) es independente de Q e igual a c. Esta concentración de sedimentos se denomina la última concentración de sedimentos (Ponce, 1988). El valor m = 1 es el mínimo el cual logran alcanzar corrientes típicas bajo flujos suficientemente altos (ASCE, 1975: p. 476).

Una reconocida formula de transporte de sedimentos es la siguiente (Colby, 1964):

q_s = k ρ vⁿ

(3)

en la cual q_s = descarga de sedimentos por unidad de ancho de la corriente; k = parámetro de transporte de material de lecho, el cual es función de las propiedades del sedimento, incluyendo tamaño del sedimento y gravedad específica; ρ = densidad del agua; v = velocidad media; y n = exponente (Ponce, 2014a).

Colby (1964) ha mostrado que n ≅ 7 es típico de flujos bajos, mientras que n ≅ 3 es típico de flujos altos. De hecho, n = 3 es un valor asimptótico característico el cual convierte en adimensional el parametro k en la Ec. 4:

q_s = k ρ v³

(4)

Debido a que n = 3 está típicamente asociado con descargas altas, la Ec. 4 puede ser usada para calcular la última concentración de sedimentos.

La descarga de agua, por unidad de ancho, es:

q = v d

(5)

en la cual d = profundidad de flujo.

La Ecuación 1 se expresa en términos de variables de ancho unitario como sigue:

q_s
C_s = ^_____
q

(6)

La sustitución de las Ecs. 4 y 5 en la Ec. 6 lleva a la ecuación que expresa la última concentración de sedimentos C_s' :

C_s' = k F² γ

(7)

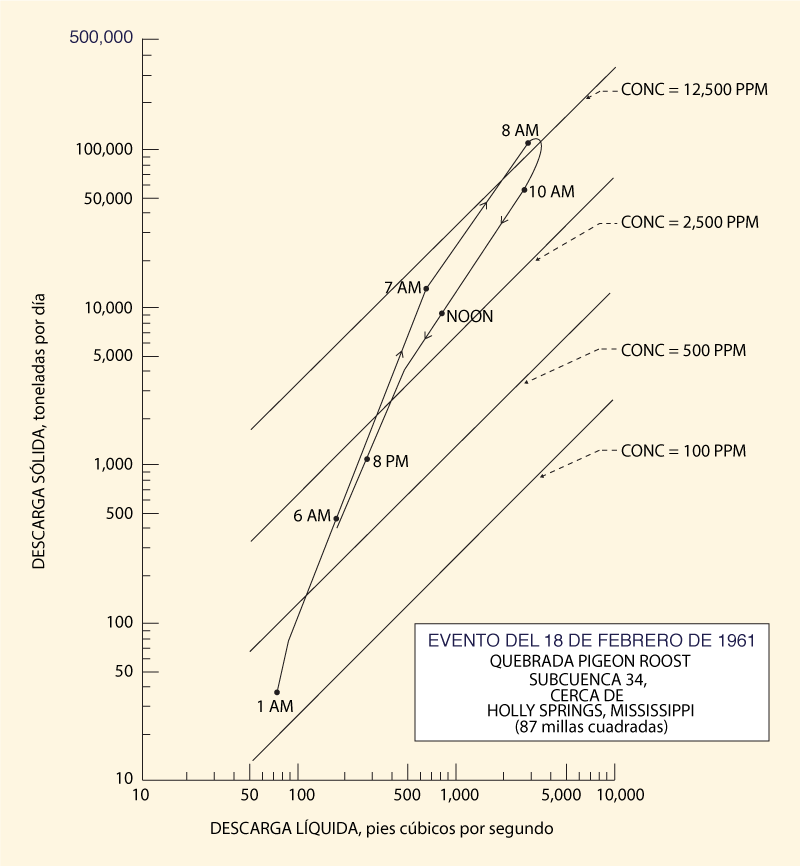
en la cual F = número de Froude, definido como F = v /(gd )^1/2; g = aceleración gravitacional; y γ es el peso específico del agua (γ = ρ/g). Por ejemplo, con k = 0.1, F = 0.4, y γ = 1,000 mg/L, la Ec. 7 lleva a lo siguiente: C_s' = 0.1 × 0.16 x 1,000 g/L = 16 g/L = 16,000 ppm.

La Figura 3 muestra una curva de gasto de sedimentos para la Cuenca 34, con un área igual a 87 millas cuadradas, en Pigeon Roost Creek, cerca de Holly Springs, Mississippi, medida durante la tormenta del 18 de febrero de 1961. [Esta figura ha sido extraída de la p. 476, Capítulo IV-C del Manual de Ingeniería de Sedimentos de la ASCE No. 75]. Las isolíneas de concentración de sedimentos se muestran como referencia. El gráfico muestra la aproximación asintótica de la curva de gasto de sedimentos a una línea de igual concentración (orientación de 45°). En este ejemplo, el valor de la última concentración de sedimento supera el valor de 12.500 ppm. El gráfico muestra que existe un límite para la concentración de sedimentos en suspensión para descargas suficientemente altas, lo cual es probable que ocurra durante una inundación poco frecuente.

[Hafa click en la figura para desplegar]

Redibujado del Manual ASCE No. 75, p. 476 (1975)

Fig. 3 Curva de gasto de sedimentos medida.

4. NATURALEZA DE UNA CURVA DE GASTO DE SEDIMENTOS

Hemos establecido que una curva de gasto de sedimentos tiene característicamente una forma curva, en la cual para valores bajos de Q la pendiente (Q_s /Q) es bastante alta, típicamente alrededor de 7, y que tiene la tendencia a disminuir progresivamente con un aumento en Q, alcanzando eventualmente un límite inferior de 3 para una descarga Q suficientemente alta (Fig. 3). Hay una razón para este comportamiento típico de una curva de gasto de sedimentos. Lo explicamos afirmando los siguientes hechos, los cuales han sido confirmados por amplia teoría y experiencia.

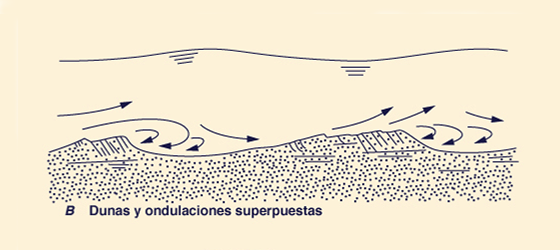
Hecho No. 1. Con flujos lo suficientemente bajos, las corrientes aluviales transportan el material del lecho en una concentración que crece constantemente al aumentar Q. En los flujos bajos, tanto la fricción de grano como la de forma están presentes, ya que las bajas velocidades del flujo son propicias para el desarrollo de la fricción de forma, manifestada como dunas y ondas superpuestas. En efecto, la configuración del lecho resulta ser ondulaciones sobrepuestas sobre dunas [Fig. 2 (a): A, B y C].

Hecho No. 2. Bajo flujos suficientemente altos, las corrientes aluviales transportan su carga de material de lecho a una concentración máxima constante, denominada última concentración de sedimentos (Ec. 7). Esta concentración es función de las propiedades del flujo (número de Froude F y peso específico γ) y de las propiedades del sedimento (el parámetro adimensional k). En estos flujos altos, la fricción de grano es el único tipo de fricción presente, ya que la velocidad de la corriente ya ha actuado para eliminar la fricción de forma. La configuración de lecho resultante es un lecho plano [Fig. 2 (b): E].

Hay una razón para este interesante y seguramente fascinante comportamiento físico de la curva de gasto de sedimentos. La concentración local de sedimentos de material del lecho debe reflejar la capacidad de transporte local de la corriente. Si el fondo del canal fuese rígido, la concentración de sedimentos debería ser única o casi única, es decir, no variar apreciablemente con el flujo. Sin embargo, en un canal aluvial los hechos demuestran lo contrario: Con caudales bajos, la concentración de sedimentos tiende a aumentar con el caudal. Esto se debe a que el flujo está ocupado lidiando con la fricción adicional creada por las formas de lecho de régimen inferior, es decir, la fricción de forma que se origina en las dunas y ondulaciones superpuestas [Fig. 4(a)].

En flujos bajos (régimen inferior), la presencia de formas de lecho no permite que el flujo transporte su carga máxima de sedimentos, reduciéndolo de hecho a una fracción de su valor. Por el contrario, en flujos altos, la rapidez de la corriente actúa para obliterar las formas del lecho, reduciendo la fricción de fondo a únicamente la fricción de grano [Fig. 4 (b)]. Esto permite que el flujo alto eventualmente alcance a transportar la máxima carga de sedimentos posible.

Un espléndido corolario del presente análisis puede expresarse de la siguiente manera: Si no fuera por las formas de lecho del régimen inferior, todo el problema del transporte de sedimentos podría resumirse en la Ec. 7, es decir, el cálculo del transporte de sedimentos recurriendo simplemente a un único valor de concentración de sedimentos: La última concentración de sedimentos.

[Haga click encima de la figura para desplegar]

Extraido de Simons y Richardson (1966)

Fig. 4 (a) Configuración de dunas y ondulaciones superpuestas.

[Haga click encima de la figura para desplegar]

Extraido de Simons y Richardson (1966)

Fig. 4 (b) Configuración de lecho plano.

Cerramos esta sección con una apropiada cita del Prof. Hans A. Einstein (1950), p. 9:

"La parte de la energía que corresponde a la resistencia de forma se transforma en turbulencia en el vórtice, a una distancia considerable del lecho. Por lo tanto, esta energía no contribuye al movimiento de la carga de fondo de las partículas y puede ignorarse en gran medida en el cálculo del transporte de sedimentos." (Las cursivas son del autor).

Está claro que Einstein consideró adecuado no incluir la energía gastada en superar las formas de fondo del régimen inferior en su reconocida fórmula de carga de sedimentos de fondo. Este hecho subraya el concepto de que la última concentración constituye un límite superior para la concentración de sedimentos, lo cual confirma la verdadera naturaleza de la curva de gasto de sedimentos.

5. VERIFICACIÓN CON DATOS DE CAMPO

Ponce y otros (2012) han utilizado un conjunto bastante elaborado de datos compilados originalmente por Williams (1995) para comparar seis (6) curvas de gasto de sedimentos medidas con los correspondientes valores de fricción de Manning medidos. El objetivo ha sido determinar la relación inversa entre la cantidad de transporte de sedimentos y la fricción de fondo: Cuanto mayor es esta última, menor es la correspondiente descarga de agua y sedimentos, y viceversa.

El siguiente conjunto de datos (Brownlie 1981a, 1981b) fueron utilizados por Ponce y otros (2012):

63 datos del Río Atchafalaya.

40 datos del Río Niobrara.

38 datos del Río Middle Loup.

51 datos del Río Grande.

156 datos del Río Mississippi.

29 datos del Río Red.

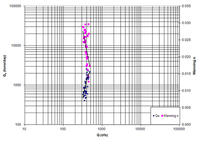
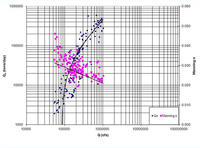
La Figura 5 muestra las curvas de gasto de sedimentos medidas, incluidos gráficos de mejor ajuste. Además, para cada conjunto de datos, se utilizaron la descarga de agua, el ancho del canal, la profundidad hidráulica y la pendiente del fondo para calcular los valores de n de Manning (Ponce, 2014b). Estos valores del n de Manning se trazaron en un eje aritmético secundario, de manera que las tendencias en la curva de gasto de sedimentos y la fricción de fondo pudieran ser comparadas. En todos los casos, se ve claramente que el valor de n de Manning disminuye a medida que aumenta la descarga de sedimentos, lo que confirma el hecho de que una mayor fricción de fondo conduce a una menor descarga de sedimentos, y viceversa.

♦ Haga click en cada figura para desplegar ♦

(a)

(b)

(c)

(d)

(e)

(f)

Fig. 5 Curvas de gasto de sedimentos y los valores correspondientes de n de Manning
(los datos de fricción se muestran en color magenta) (Ponce y otros, 2012).

6. CONCLUSIONES

Se ha revisado, explicado y aclarado la naturaleza de una curva de gasto de sedimentos. La última concentración de sedimentos es la concentración máxima que se puede alcanzar en ausencia de la fricción de fondo. Su valor se puede calcular directamente en función de las propiedades del flujo y del sedimento utilizando la Ecuación 7.

La forma de la curva de gasto de sedimentos constituye efectivamente una curva en la cual la pendiente es alta para los caudales inferiores, alrededor de 7, y disminuyendo asintóticamente para los caudales superiores hasta el valor característicamente bajo de 3. Este comportamiento es una consecuencia directa del aumento de la fricción de fondo, el cual es atribuible a las formas de rugosidad del lecho en el régimen inferior, es decir, dunas y ondulaciones superpuestas. Estas últimas interfieren con el potencial del flujo para transportar la última concentración de sedimentos, reduciendo así la descarga de sedimentos.

El análisis anterior aclara el motivo de la caída en el transporte de sedimentos para flujos bajos y, por lo tanto, explica la forma de una curva típica de gasto de sedimentos. Una verificación con datos de campo confirma los hallazgos de este estudio: Cuanto mayor es la fricción total del lecho (fricción de fondo), menor es la cantidad de sedimentos transportados, y viceversa.

BIBLIOGRAFÍA

ASCE, 1975. Sedimentation Engineering. Manuals and Reports on Engineering Practice, Manual 54, Vito A. Vanoni, editor, New York.

ASCE, 1975. Sedimentation Engineering. Manuals and Reports on Engineering Practice, Manual 54: p.476.

ASCE, 2007. Sedimentation Engineering: Processes, Measurements, Modeling, and Practice. Manuals and Reports on Engineering Practice, Manual 110, Marcelo H. Garcia, editor, New York.

Brownlie, W. L. (1981a). Prediction of flow depth and sediment discharge in open channels. Report KH-R-43A, W.M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology, Pasadena, California.

Brownlie, W. L. (1981b). Compilation of alluvial channel data: Laboratory and field. Report KH-R-43B, W.M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology, Pasadena, California.

Colby, B. R. 1964. Discharge of sands and mean velocity relations in sand-bed streams. U.S. Geological Survey Professional Paper 462-A, Washington, DC.

Einstein, H. A. (1950). The bed-load function for sediment transportation in open-channel flows. USDA Soil Conservation Service, Technical Bulletin No. 1026, Washington, DC, September.

Kennedy, J. F. 1983. Reflections on rivers, research, and Rouse. Journal of Hydraulic Engineering ASCE, 109(10), 1257-1260.

Ponce, V. M. 1988. Ultimate sediment concentration. Proceedings, National Conference on Hydraulic Engineering, Colorado Springs, Colorado, August 8-12, 311-315.

Ponce, V. M. 1995. Hydrologic and environmental impact of the Parana-Paraguay waterway on the Pantanal of Mato Grosso, Brazil. https://ponce.sdsu.edu/hydrologic_and_environmental_impact_of_the_parana_paraguay_waterway.html

Ponce, V. M., D. S. Smith, y R. D Aguilar. 2012. Effect of form friction on the sediment rating curve. Online article.
https://ponce.sdsu.edu/effect_of_form_friction.html

Ponce, V. M. 2014a. Engineering Hydrology: Principles and Practices. Online textbook.
https://ponce.sdsu.edu/enghydro/index.html

Ponce, V. M. 2014b. Fundamentals of Open-channel Hydraulics. Online textbook.
https://ponce.sdsu.edu/openchannel/index.html

Simons, D. B., y E. V. Richardson. 1966. Resistance to flow in alluvial channels. Geological Survey Professional Paper 422-J, U.S. Government Printing Office, Washington, D.C.

Williams, D. T. (1995). Selection and predictability of sand transport relations based upon a numerical index. Ph.D. dissertation, Department of Civil Engineering, Colorado State University, Fort Collins, Colorado.

231208