Observamos que el diseño de un canal revestido para el control de ondas de rollo puede lograrse mediante una elección juiciosa de la forma de la sección transversal. Con este fin, es necesario elegir, en la etapa de diseño, una forma de canal que reduzca efectivamente el número de Vedernikov por debajo del valor de 1 (V < 1). Por lo tanto, el enfoque de diseño debe centrarse en el valor de β, el exponente de la curva de gasto, parámetro definido en términos de V/F.

En este artículo usamos la calculadora en línea canalenlinea15b, la cual determina los valores de β, F y V para un canal prismático (Ponce y Boulomytis, 2021). Corremos la calculadora para una serie de formas de sección transversal, incluidas trapezoidales y rectangulares, manteniendo constantes las siguientes variables: (1) caudal Q, (2) n de Manning, y (3) pendiente de fondo S. El efecto de la forma de la sección transversal se examina corriendo la calculadora para varios valores apropiados de pendiente lateral z (z H: 1 V), y una serie de anchos de fondo b, fijando la profundidad de flujo y para que corresponda con el caudal Q adoptado.

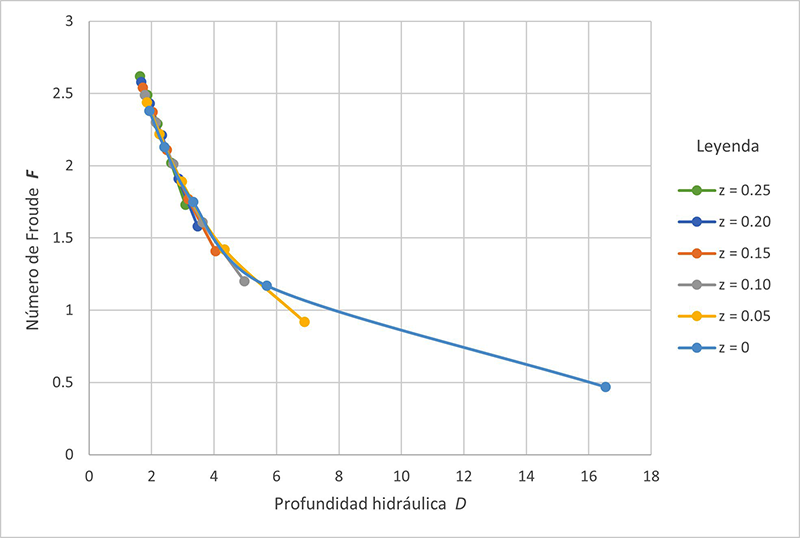
El objetivo es examinar el comportamiento y la sensibilidad de las variables de flujo a los números de Froude F y de Vedernikov V, y al valor asociado de β. En la práctica, se puede demostrar que la estabilidad hidrodinámica se alcanza para valores de β cercanos pero superiores a 1. Por lo tanto, la sección transversal óptima, desde el punto de vista de la estabilidad, corresponde al valor más bajo de β, superior a 1, que sea compatible con el costo del proyecto, las dimensiones sobre el terreno, y otras consideraciones afines.

2.  ANTECEDENTES

La teoría de la estabilidad hidrodinámica del flujo en canales abiertos se debe a Vedernikov (1945). Varios años más tarde, Craya aclaró el criterio de Vedernikov al establecerlo en términos de la celeridad de las ondas (Craya, 1952). El criterio de Vedernikov-Craya establece que la aparición de ondas de rollo se formará cuando la celeridad de Seddon iguale o exceda la celeridad de Lagrange, es decir, cuando la celeridad de la onda cinemática, gobernada por las fuerzas de gravitación y de fricción, iguale o exceda la celeridad de la onda dinámica, gobernada por fuerzas de inercia y del gradiente de presiones. En este caso, el número de Vedernikov es mayor o igual a 1: V ≥ 1. Por el contrario, cuando V < 1, las ondas dinámicas viajan más rápido que las ondas cinemáticas y, en consecuencia, el flujo permanece estable.

En 1907, Cornish mostró, aparentemente por primera vez, una fotografía del fascinante fenómeno en un artículo publicado en el Journal of the Royal Geographical Society (Fig. 2) (Cornish, 1907). En 1948, Powell bautizó el concepto, al afirmar: "Este criterio, al que llamo número de Vedernikov..." (Powell, 1948). Posteriormente, Ven Te Chow se refirió al fenómeno como la "inestabilidad del flujo uniforme", lo que implica que bajo ciertas condiciones, el flujo puede volverse inestable y romperse en un tren de ondas (Chow, 1959: Sección 8.8).

Cornish

Fig. 2  Tren de ondas de rollo observadas en un canal en los Alpes suizos a principios del siglo XX (Cornish, 1907).

Los roles de la masa y la energía son fundamentales para comprender el desarrollo de las ondas de rollo. Mientras que las ondas cinemáticas transportan masa, las ondas dinámicas transportan energía (Lighthill y Whitham, 1955). Por lo tanto, las ondas de rollo ocurren cuando la celeridad de transporte de masa supera a la del transporte de energía. Bajo esta óptica, las ondas de rollo son vistas como una curiosa manifestación física de la preponderancia del transporte de masa sobre el transporte de energía en el flujo no permanente en canales abiertos (Ponce y Choque Guzmán, 2019).

3.  RELACIÓN ENTRE β Y V/F

Hay tres velocidades características en la hidráulica de canales abiertos (Ponce, 1991; Ponce, 2014c):

1. La velocidad media u del flujo permanente normal, expresada por Manning o Chezy;

2. La velocidad relativa v de la onda cinemática, expresada por la celeridad de Seddon; y

3. La velocidad relativa w de la onda dinámica, expresada por la celeridad de Lagrange.

Estas tres velocidades sólo pueden definir dos proporciones, o números adimensionales, independientes, a saber, los números de Froude y Vedernikov (Ponce, 2014a).

El número de Froude es la relación entre la velocidad media del flujo normal u y la celeridad relativa de la onda dinámica w:

u                   u F  =   ____   =    ________             w            ( g D )1/2 (1)

en la cual D = profundidad hidráulica (D = A / T ); A = área de flujo; T = ancho superior; y g = aceleración gravitacional (Ponce y Choque Guzmán, 2019; Ponce y Boulomytis, 2021).

El número de Vedernikov es la relación entre la celeridad relativa de la onda cinemática v y la celeridad relativa de la onda dinámica w:

v               (β - 1) u V  =   ____   =    _________             w             ( g D )1/2 (2)

La tercera relación, la cual función de las otras dos, es la celeridad relativa adimensional de la onda cinemática v/u, expresada de la siguiente manera (Ponce y Choque Guzmán, 2019):

v                             V ____   =   β - 1  =   _____    u                             F (3)

El número de Froude de estabilidad neutra F_ne es el que corresponde al número de Vedernikov V = 1. Por lo tanto, el número de Froude de estabilidad neutra es función únicamente de β, el exponente de la curva de gasto:

La Tabla 1 muestra los valores correspondientes de β y F_ne para tres formas de sección transversal asintótica y dos tipos de fricción. La forma del canal inherentemente estable ha sido documentada, primero por Liggett (1975), y luego por Ponce y Porras (1995) (Fig. 3).

Tabla 1.  Valores de β y Fne correspondientes a tres secciones transversales asintóticas.
Sección transversal asintótica	Tipo de fricción	β	Fne
Hidráulicamente ancha	Manning	5/3	3/2
	Chezy	3/2	2
Triangular	Manning	4/3	3
	Chezy	5/4	4
Inherentemente estable	Manning o Chezy	1	∞

Ponce y Porras

Fig. 3  Sección transversal de un canal inherentemente estable.

La Ecuación 4 muestra que tal como β ⇒ 1, el número de Froude de estabilidad neutra F_ne ⇒ ∞. En la práctica, sin embargo, el número de Froude está limitado por la cantidad demostrablemente finita de la fricción de fondo, por lo que los números máximos de Froude no exceden, de manera realista, un valor en el rango de 25-30. Por lo tanto, el canal inherentemente estable debe considerarse una construcción teórica.

Sin embargo, lo que es más importante, ciertas formas de sección transversal que presentan valores de β cercanos pero superiores a 1, dan como resultado un aumento real en el valor del número de Froude de estabilidad neutra F_ne, lo que reduce efectivamente la probabilidad de que el flujo se vuelva inestable. Este razonamiento se trata en este artículo: Encontrar la forma óptima de la sección transversal, típicamente trapezoidal, que sea tanto práctica como estable.

4.  PROGRAMA DE ENSAYOS

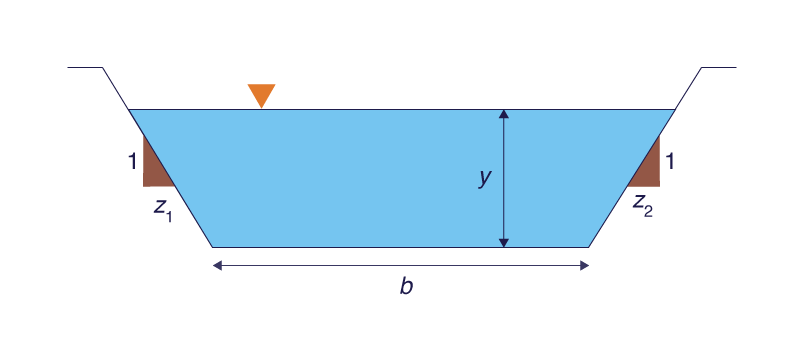
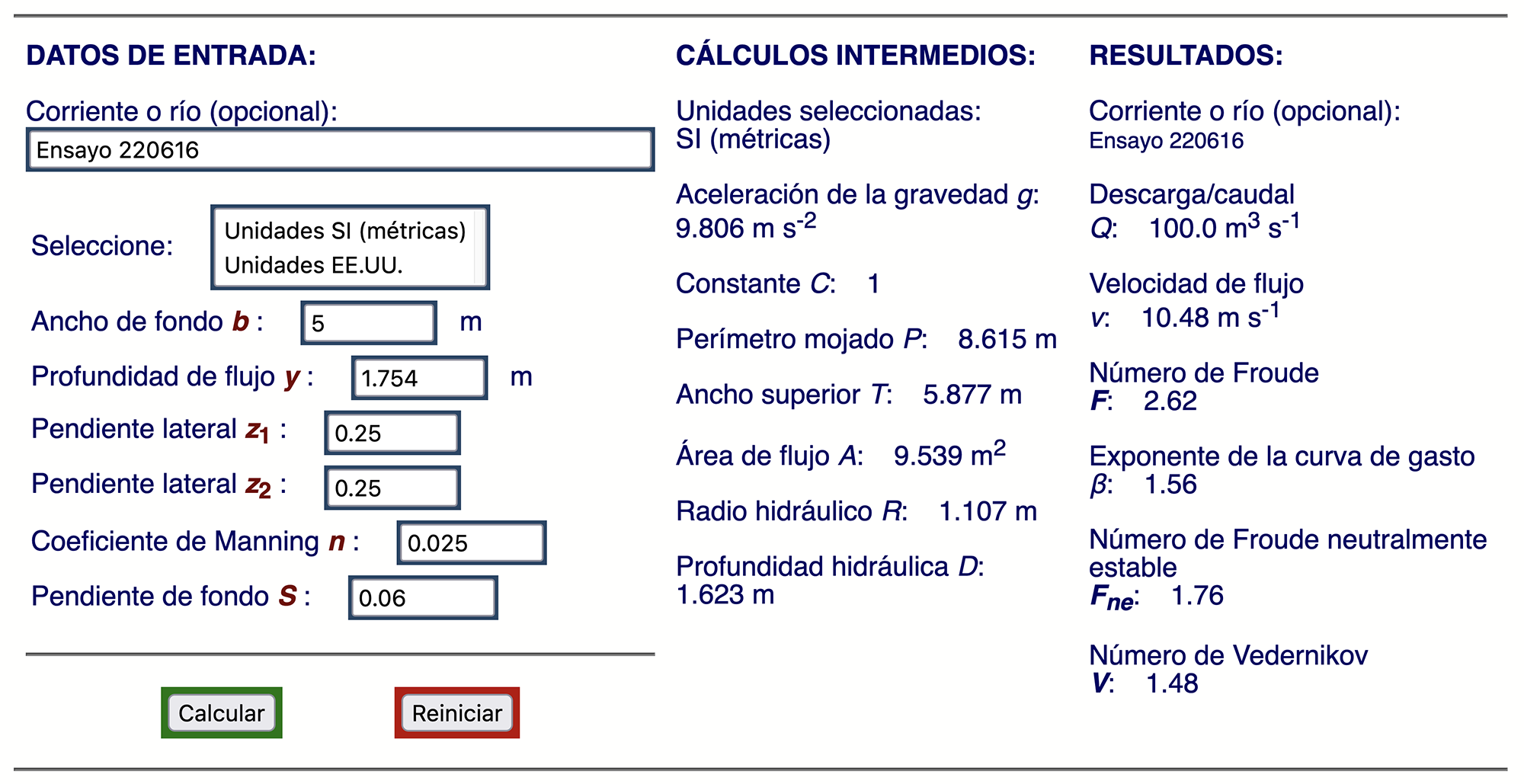
La calculadora canalenlinea15b calcula el valor de β, el exponente de la curva de gasto, correspondiente a una sección rectangular, trapezoidal o triangular. La calculadora requiere los siguientes datos de entrada (Fig. 4):

Al principio, para cada aplicación, determinar los valores aplicables de n de Manning y pendiente de fondo S. La metodología consta de los siguientes pasos:

1. Seleccionar un valor apropiado de caudal de diseño Q;

2. Seleccionar un conjunto de valores apropiados de las pendientes laterales z₁ y z₂;

3. Determinar un conjunto de prueba de valores del ancho inferior b;

4. Usando la calculadora en línea, para cada valor de ancho de fondo b, calcular, por prueba y error, la profundidad de flujo y correspondiente al caudal Q; y;

5. Tomar nota del resultado de la calculadora en línea, el cual consta de lo siguiente: (a) confirmación del valor del caudal Q; (b) velocidad de flujo v; (c) número F de Froude; (d) exponente de la curva de gasto β; (e) número de Froude de estabilidad neutra F_ns; y (f) número de Vedernikov V.

Teniendo en cuenta las consideraciones de estabilidad (V < 1) o inestabilidad (V > 1) del flujo, los resultados se analizan para elegir la forma de sección transversal óptima, compatible con consideraciones de costo y restricciones existentes en el sitio.

El programa de ensayos está diseñado para determinar las condiciones hidráulicas en una serie de secciones transversales alternativas para las cuales el número de Vedernikov calculado varía en el rango V ≷ 1. Se especifican varios valores de pendiente lateral z, que van desde alto (z = 0.25; trapezoidal) a bajo (z = 0; rectangular), y variando el ancho inferior b dentro de un rango adecuado (5 ≥ b ≥ 0). La experiencia indica que es probable que el rango elegido de pendientes laterales (0.25 ≥ z ≥ 0) proporcione un rango deseado de números de Vedernikov V para un análisis adecuado de estabilidad/inestabilidad del flujo en el canal.

Las siguientes seis (6) pendientes laterales se consideran en este estudio:

• z = 0.25;

• z = 0.20;

• z = 0.15;

• z = 0.10;

• z = 0.05; y

• z = 0.0.

Las Tablas 2 a 7 muestran los resultados del cálculo utilizando canalenlinea15b. Generalmente, cuando se reduce el ancho de fondo b en el rango elegido 5 ≥ b ≥ 1, y cuanto menor es el valor de la pendiente lateral z, más rápido disminuye el número de Vedernikov V a valores menores que 1. De hecho, la Tabla 7 muestra que el valor más bajo de V ( V = 0.05) se obtiene para el caso de z = 0 (canal rectangular) y b = 1, es decir, el valor más estrecho de b dentro del rango de ensayo (5 ≥ b ≥ 1). A continuación se presenta un análisis detallado.

5.  ANÁLISIS

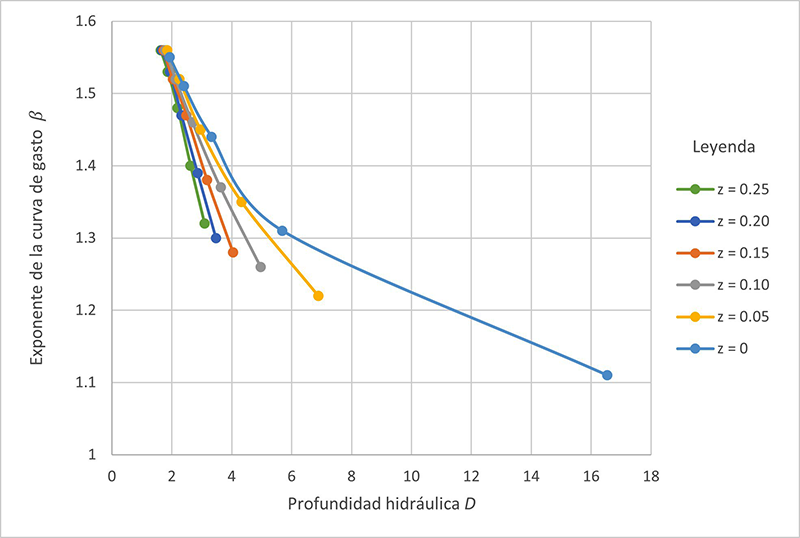
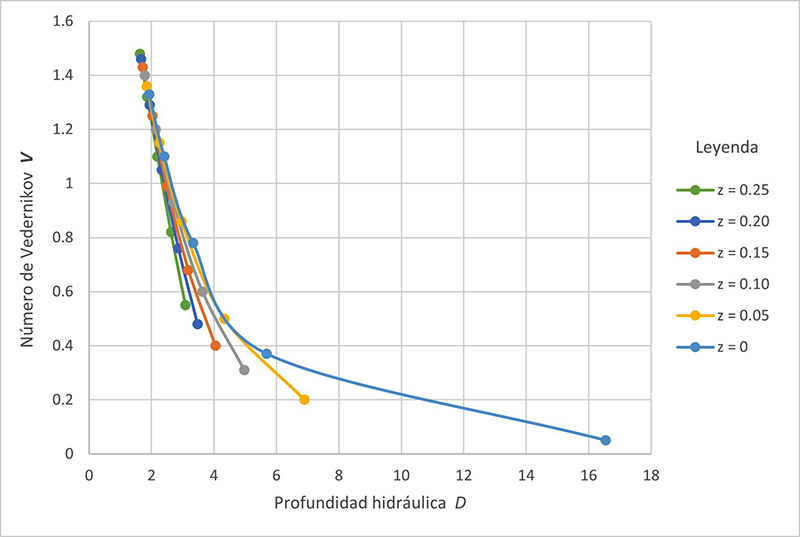
Los resultados de las Tablas 2 a 7 se analizan para determinar la forma de la sección transversal, que en este artículo varía de trapezoidal (z = 0.25; Tabla 2) a rectangular (z = 0; Tabla 7), bajo la cual el número de Vedernikov disminuye. desde el rango inestanle, V > 1, hasta el rango estanle, V ≤ 1. Puede observarse que los números de Froude y Vedernikov (Ecuaciones 1 y 2, respectivamente) varían inversamente con la profundidad hidráulica D. Por lo tanto, cuanto mayor sea el valor de D, menores serán los valores de los números de Froude y Vedernikov, lo que eventualmente conducirá a la condición de flujo estanle, es decir, V ≤ 1. Proponemos que aquí está la solución de la dicotomía estabilidad/inestabilidad: Cuanto mayor sea la profundidad hidráulica D, más estable será el flujo.

Para explicar mejor los hallazgos de este trabajo, la variación, con la profundidad hidráulica D, del exponente β, el número de Froude F, y el número de Vedernikov V se muestran en las Figs. 6 a 8, respectivamente.

La Figura 6 muestra que la disminución de β es gradual para las formas trapezoidales (0.25 ≥ z ≥ 0.05), y marcada (hasta β = 1.11) para la forma rectangular asintótica (z = 0). La Figura 7 muestra que la disminución de F es gradual para las formas trapezoidales (0.25 ≥ z ≥ 0.05), y marcada (hasta F = 0.47) para la forma rectangular asintótica (z = 0). La Figura 8 muestra que la disminución de V es gradual para las formas trapezoidales (0.25 ≥ z ≥ 0.05), y marcada (hasta V = 0.05) para la forma rectangular asintótica (z = 0).

Se concluye que la forma más rápida de disminuir el número de Vedernikov por debajo de 1 y, por lo tanto, asegurar la estabilidad hidrodinámica, es elegir un ancho de fondo b, en conjunto con una pendiente lateral z, que asegure que V < 1.

En la práctica, se puede utilizar como objetivo de diseño un valor apropiado de V < 1. Los resultados de las Tablas 2 a 7 indican que, para el ejemplo aquí presentado, se obtiene un V = 0.93 para b = 3 m y z = 0.10. Además, para b = 3 m y z = 0.05, se obtiene un V = 0.86, algo más bajo y, por lo tanto, más estable.

El análisis presentado aquí considera sólo la cuestión de la estabilidad hidrodinámica. En una situación actual de diseño, otras consideraciones, como el costo, la huella geométrica del proyecto, y la facilidad de construcción pueden desempeñar un papel importante en la elección de la óptima forma de la sección transversal.

Fig. 6  Exponente de la curva de gasto β  vs. profundidad hidráulica D.

Fig. 7  Número de Froude F  vs. profundidad hidráulica D.

Fig. 7  Número de Vedernikov V  vs. profundidad hidráulica D.

6.  CONCLUSIONES

Se realiza un estudio del efecto de la forma de la sección transversal sobre la estabilidad o inestabilidad hidrodinámica del flujo en un canal abierto. Se identifican como las variables de control el exponente de la curva de gasto β, el número de Froude F, y el número de Vedernikov V. El exponente de la curva de gasto caracteriza la relación entre el caudal y el área de flujo (Q = α A ^β). El número de Froude caracteriza el régimen de flujo como: (a) subcrítico, (b) crítico, o (c) supercrítico. El número de Vedernikov describe un tipo de flujo que puede ser: (a) estable, (b) neutro, o (c) inestable.

Para el análisis se especifica un canal revestido y empinado. El caudal de diseño seleccionado es Q = 100 m³/s, con pendiente de fondo S = 0.06, y n de Manning = 0.025, similar a las condiciones hidráulicas en el río Huayñajahuira, en La Paz, Bolivia, en el cual las ondas de rollo se repiten con preocupante regularidad. El programa de prueba considera la variación del ancho del fondo b en el rango 5 ≥ b ≥ 1, en intervalos de 1 m, y la pendiente lateral z en el rango 0.25 ≥ z ≥ 0, en intervalos de 0.05.

La calculadora canalenlinea15b se utiliza para calcular las variables hidráulicas, que culminan en los valores del exponente de la curva de gasto β, el número de Froude F, y el número de Vedernikov V, para cada uno de treinta (5 × 6 = 30) casos. Los resultados demuestran de manera concluyente que a medida que el ancho del canal b se reduce de 5 a 1 m, y la pendiente lateral z se reduce de 0,25 a 0, los valores calculados de β, F, y V se reducen, primero gradualmente, y luego marcadamente, a medida que z → 0. Para una aplicación dada, estos hallazgos pueden usarse para determinar los valores óptimos de ancho de fondo b y pendiente lateral z que aseguren que V < 1, evitando así la inestabilidad hidrodinámica del flujo y las ondas de rollo normalmente asociadas con esta condición.

REFERENCIAS BIBLIOGRÁFICAS

Craya, A. 1952. The criterion for the possibility of roll wave formation. Gravity Waves, Circular 521, 141-151, National Institute of Standards and Technology, Gaithersburg, MD.

Cornish, V. 1907. Progressive waves in rivers. Journal of the Royal Geographical Society, Vol. 29, No. 1, January, 23-31.

Liggett, J. A. 1975. Stability. Chapter 6 in Unsteady Flow in Open Channels, K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Ft. Collins, Colorado.

Lighthill, M. J. y G. B. Whitham. 1955. On kinematic waves: I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.

Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.

Ponce, V. M. y P. J. Porras. 1995. Effect of cross-sectional shape on free-surface instability. Journal of Hydraulic Engineering, ASCE, Vol. 121, No. 4, April, 376-380.

Ponce, V. M. 2014a. Sección 1.3  en Fundamentos de Hidráulica de Canales, texto en línea.

Ponce, V. M. 2014b. Sección 11.4  en Fundamentos de Hidráulica de Canales, texto en línea.

Ponce, V. M. 2014c. Chow, Froude, and Vedernikov. Proceedings, American Society of Civil Engineers (ASCE) World Environment and Water Resources Congress, June 1-5, 2014, Portland, Oregon.

Ponce, V. M. y B. Choque Guzmán. 2019. The control of roll waves in channelized rivers. http://ponce.sdsu.edu/the_control_of_roll_waves.html

Ponce, V. M. y V. Boulomytis, 2021. Design of a stable channel on a steep slope using the exponent of the rating. http://ponce.sdsu.edu/design_of_a_stable_channel_using_the_exponent_of_the_rating.html

Powell, R. W. 1948. Vedernikov's criterion for ultra-rapid flow. Transactions, American Geophysical Union, Vol. 29, No. 6, 882-886.

Vedernikov, V. V. 1945. Conditions at the front of a translation wave disturbing a steady motion of a real fluid, Dokl. Akad. Nauk SSSR, 48(4), 239-242.