1. INTRODUCTION
The question of how much water could be
pumped from an aquifer and still remain sustainable has no
straightforward answer. At first, the decision seems to be one
related to hydrogeology. A careful examination, however, reveals a host of other issues,
among which some of the more significant are:
How does the decision affect surface vegetation?
How does it affect the relation between surface and groundwater?
How does it affect pertinent water rights?
How does it affect land subsidence and salt-water intrusion?
(Ponce, 2006).
In the past two decades, it has become patently clear that the sustainability of an aquifer
has little to do with its hydrogeologic
properties (Alley et al., 1999).
Instead, the focus is now seen to be
on ecosystem conservation and established water rights
(Ponce, 2014a).
This paradigm shift follows from the realization that groundwater is not a volume
to be mined, but rather a flow to be acknowledged. In his seminal paper on hydrogeology, Theis (1940) wrote:
"All ground water of economic importance is in the process of moving
from a place of recharge to a place of discharge. Under natural conditions,
prior to the development of wells, aquifers are in a state of dynamic equilibrium.
Discharge by wells is a new discharge superimposed upon a previously stable system,
and it must be balanced by: (a) an increase in recharge, (b)
a decrease in discharge, (c) a loss of storage,
or (d) a combination of these."
In this article, we endeavor to make the case for the quantification of
groundwater sustainability.
2. GROUNDWATER FLOW EXPLAINED
Groundwater flow is extremely complex, varying in space (in three dimensions) and time (through various spans).
Aquifers may be broadly classified as:
At the outset, we acknowledge that
all groundwater is constantly in motion from
a zone of higher potential to a zone of lower potential, with the
ultimate fate of groundwater being the nearest
ocean. However,
depending on the terrain's geomorphology,
groundwater could eventually exfiltrate as
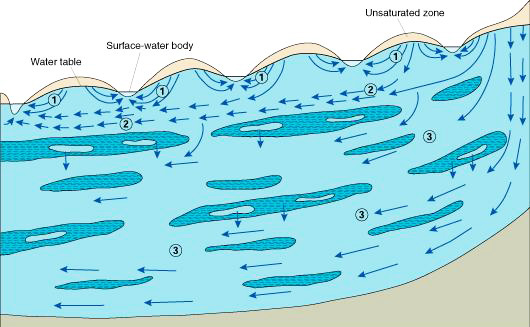
the moisture of wetlands or the baseflow of rivers (Fig. 1). It is clear that surface water
and groundwater are intrinsically connected: Groundwater may actually become surface
water in space and time, and vice versa. Therefore, exploitation of groundwater
could eventually affect the surface water and other components of the
hydrologic cycle in the vicinity (Ponce, 2014a).
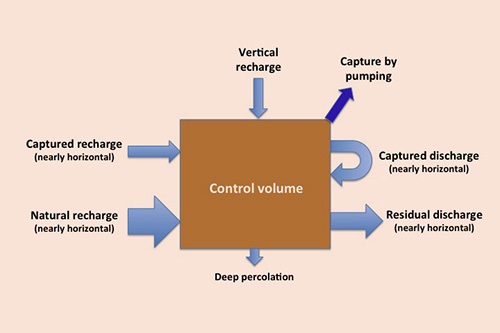
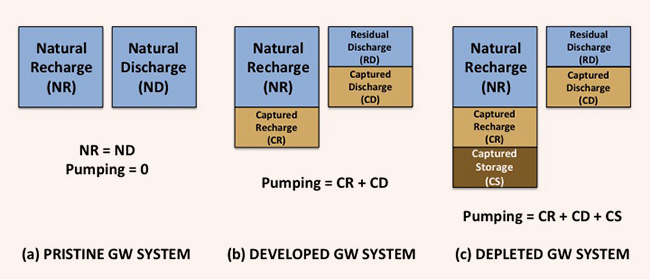
To further compound the problem's complexity, we reckon that a groundwater analysis suffers from a decided limitation: The size of the control volume is not fixed. Since all groundwaters are ultimately connected, defining the limits of a control volume is perforce an arbitrary exercise. Unlike surface water, which is constrained to the applicable watershed or basin boundary, there is no similar boundary for groundwater flow. Pumping without limit will generally result in an ever increasing size of the cone of depression (Prudic and Herman, 1996; Ponce and Vuppalapati, 2015). Echoing Theis' statement, we reiterate that groundwater is not a volume, but a flow. An arbitrarily defined control volume will have: (1) inflow (recharge), (2) outflow (discharge), and (3) stored volume of groundwater (water filling the soil or rock voids). Pumping constitutes an external demand, with its discharge originating in any or all of the three components mentioned above. Under this optic, three scenarios are possible (Fig. 2):
In a typical groundwater system,
recharge consists of all flow entering the control volume.
Note that in a highly developed system, the vertical recharge may include amounts of artificial groundwater replenishment and/or soil leaching amounts (Ponce, 2007). Discharge from the control volume consists of:
Amounts of deep percolation are largely intractable and generally considered to be a relatively small fraction of precipitation (a global average of about 2%) and, therefore, negligible on practical grounds (L'vovich, 1979). In other words, deep percolation is the (small) fraction of precipitation that is effectively lost from the surface waters. Figure 3 shows a schematic of the various fluxes relevant to groundwater flow.
3. SUSTAINABLE USE OF GROUNDWATER The central issue of sustainability is the question of how much water to pump from an aquifer and still remain sustainable (Alley et al., 1999). In the typical case, aquifer replenishment is slow, taking decades, if not hundreds or thousands of years. Thus, it follows that excessive pumping of groundwater may lead to depletion and the consequent lack of sustainability. A depleted aquifer is one that cannot recover fast enough to continue to be of use; therefore, it is unsustainable. Since an aquifer may be depleted through excessive pumping, it may be argued that the solution is to leave the aquifers alone and use only surface waters. Unlike groundwaters, the recycling time of surface water is a global average of 11 days (L'vovich, 1979; Ponce et al., 2000); therefore, all surface waters are sustainable when compared to groundwaters. This approach, while apparently logical, does away with the practice of groundwater pumping established for the past century in developed societies. We argue here that this extreme solution is politically incorrect. Groundwater use should not be altogether suspended; rather, it should be regulated with the aim to manage, mitigate, and/or minimize depletion and other negative effects in order to best meet the challenge of sustainability. The discussion then shifts to the components of the groundwater balance. Where should the pumped water come from? We note that there is a caveat in the hydrologic balance. The water extracted by pumping could be either:
Irrigated agriculture is the classical example of consumptive use, particularly when the drainage waters (drainage is ostensibly a necessity in arid/semiarid regions) are collected and removed from the premises via surface flow (Fig. 4). Other uses (domestic or industrial) may be totally or partially consumptive, depending on the local situation.
While the concept of sustainable yield has only been recently recognized (Alley et al., 1999), the admittedly older concept of safe yield has been around for nearly a century. Lee (1915) defined "safe yield" as the limit to the quantity of water which can be withdrawn from an aquifer, regularly and permanently, without dangerous depletion of the storage reserve. He noted that water permanently extracted from an underground reservoir reduces the volume of water passing through the basin by way of natural channels, i.e., the natural discharge. To illustrate the existence of this natural discharge, Lee observed that heavy pumping would commonly result in the drying up of springs and wetlands (Ponce, 2014). Thus, he distinguished between a theoretical safe yield, equal to the natural recharge, and a practical safe yield, a lower value which takes into account the need to maintain a residual discharge (Fig. 2). According to Lee, the residual discharge must be ascertained and deducted from the theoretical safe yield in order to obtain the practical safe yield. Over the past two decades, the latter has morphed into sustainable yield, which reaches beyond hydrogeology. How much should the residual discharge be when assessing sustainable yield? In cases when the captured discharge must be minimized due to the existence or claims of downstream water rights (i.e., springs, wetlands, and baseflow), it follows that very little or none of the nearly horizontal recharge could be captured without encroachment on the rights of others. Under nonequilibrium conditions, pumping one-hundred percent of the natural recharge could approximately result in the capturing of up to 50% of the natural discharge (Fig. 2). Under equilibrium conditions, any amount of capture would come from discharge and possibly encroach upon established downstream rights.
This bleak picture is somewhat ameliorated when it is recognized
that the vertical discharge, i.e., the fraction of local precipitation
that manages to reach the water table, is not specifically included
in the determination of (nearly horizontal) recharge.
Thus, a resolution of the conflict
of rights between surface water and groundwater would be the capture of any of the vertical recharge.
4. THE CYBERNETIC HYDROLOGIC BALANCE
Ir order to properly quantify vertical recharge and, therefore, gain a handle on
sustainable groundwater yield,
we resort to L'vovich's cybernetic
hydrologic balance, an approach better suited for yield
hydrology than the conventional one (L'vovich, 1979;
Ponce, 2018).
In L'vovich's
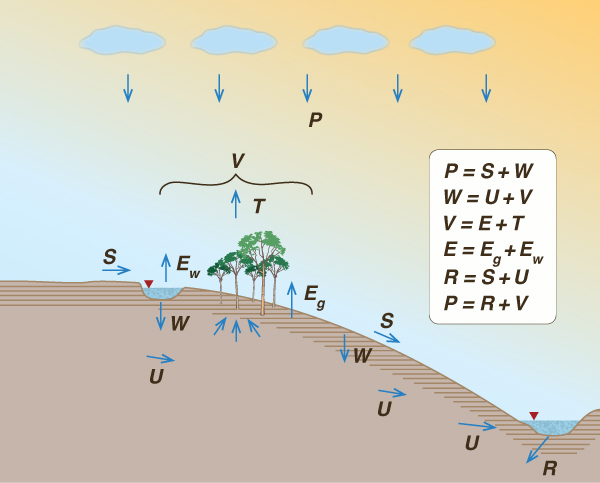
approach, annual precipitation P is separated into two components (Fig. 5):
in which S = surface runoff, i.e., the fraction of runoff originating on the land surface, and
In turn, wetting is separated into two components:
in which U = baseflow, i.e., the fraction of wetting which exfiltrates as the dry-weather flow of streams and rivers, and V = vaporization, i.e., the fraction of wetting returned to the atmosphere as water vapor. Runoff (i.e., total runoff) is the sum of surface runoff and baseflow:
Combining Eqs. 1 to 3:
Equations 1 to 4 constitute a set of water balance equations. Four water balance coefficients may be defined: (1) runoff coefficient, (2) baseflow coefficient, (3) wetting coefficient, and (4) recharge coefficient. The runoff coefficient is:
The baseflow coefficient is:
The wetting coefficient is:
The groundwater recharge coefficient is:
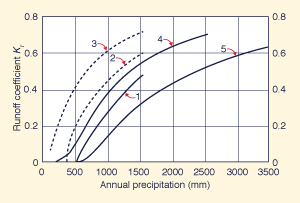
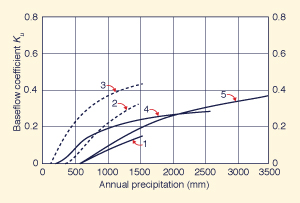
Figure 6 shows runoff and baseflow coefficients calculated by Ponce and Shetty (1995), based on data reported by L'vovich (1979). It is seen that in five all cases, runoff and baseflow coefficients increase with annual precipitation.
5. EXAMPLE APPLICATION
The methodology described in the previous section is applied herein
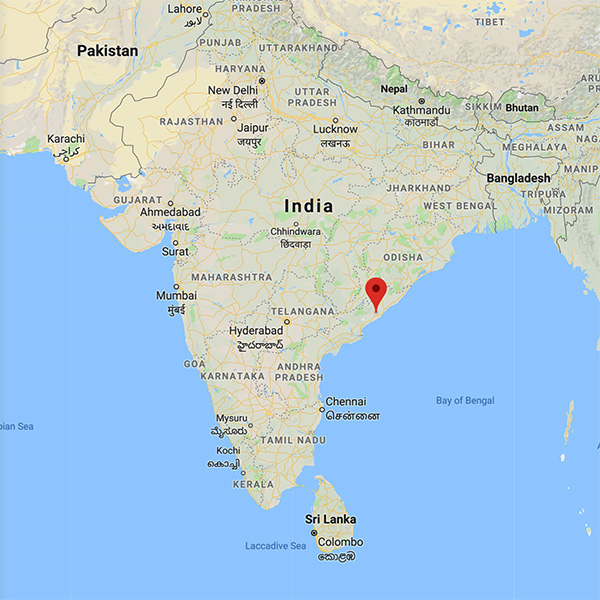
to data from the
Sarada river basin, upstream of Anakapalli, in Andhra Pradesh, India (Fig. 7).
The basin is positioned between the Eastern Ghats
and the eastern coastline of India, and features a
subhumid climate (Ponce et al., 2000), with a drainage area of 1,980 km2.
Eleven (11) years of rainfall-runoff data are
analyzed. The precipitation data consists of a daily rainfall hyetograph and
the runoff data consists of the hydrograph measured at the basin outlet.
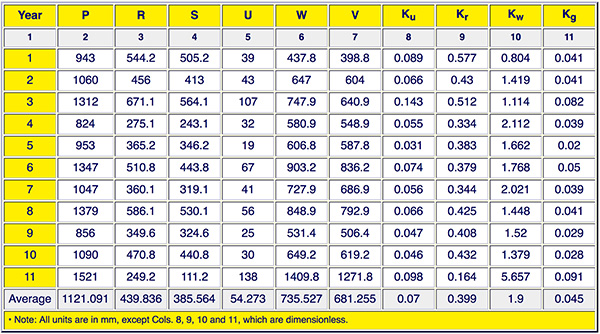
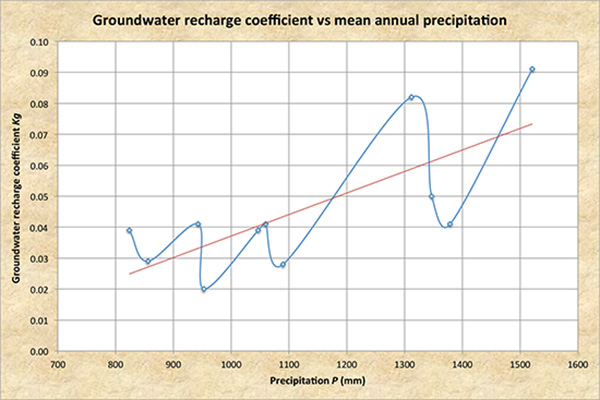
The annual hyetographs are used to calculate annual rainfall Figure 8 shows the tabular results of the online program, where the groundwater recharge coefficient Kg is given in Col. 11. Figure 9 plots Kg vs mean annual precipitation P, in ascending order of precipitation. Despite the apparent noise in the data, the general trend is for an increase in Kg with an increase in P.
6. RECHARGE COEFFICIENTS
AND SUSTAINABLE YIELD
The vertical groundwater recharge coefficient
is the fraction of precipitation that manages to reach the groundwater table.
Given mean annual
precipitation, and, for that matter, given any amount of annual precipitation, the recharge coefficient
may be interpreted as the amount of water that could be captured by pumping while assuring
a sustainable yield.
This strategy does not compromise any part of the (nearly horizontal) recharge
or discharge. Note that the conversion of discharge to recharge (in a control volume)
has been a point of contention in groundwater resource evaluations for many decades (Kazmann, 1956).
For any one watershed/basin, the
recharge coefficient may be evaluated following the cybernetic hydrologic balance
described herein (Ponce, 2018). Given the natural
hydrologic variability, in any one year,
the sustainable groundwater yield, i.e., the permissible
amount of capture, could be practically based on the amount of precipitation occurring
in the previous year. Amounts of artificial replenishment
and/or return flows,
if any, may be added to the (natural) vertical recharge
at this time (Ponce, 2007).
7. SUMMARY AND CONCLUSIONS
The concepts of safe yield and sustainable yield of groundwater
are analyzed and compared
in the context of a hydrologic balance. All recharge and discharge fluxes
are duly accounted for.
A methodology to evaluate vertical recharge is developed and tested.
The methodology is based on the cybernetic hydrologic balance of L'vovich (1979),
including the definition of
a groundwater recharge coefficient. This coefficient
represents the fraction of precipitation that reaches the water table;
therefore, it may be used to evaluate and assess
sustainable groundwater yield.
Any amount of groundwater capture over and above the vertical recharge would have to
demonstrate, by means of suitable hydrological (baseflow) and ecohydrological (ecosystems) studies,
that it does not significantly affect established rights.
The online calculator online water balance 2 rounds up the analysis.
ACKNOWLEDGMENTS
The authors wish to recognize Donna Tisdale and the people of the
community of Boulevard,
in southeast San Diego County, California, for
their support of theoretical and applied
research in groundwater
sustainability throughout the past 12 years.
The Sarada river basin data used in this study was provided by
REFERENCES
Alley, W. M., T. E. Reilly, and O. E. Franke. 1999. Sustainability of groundwater resources. U.S. Geological Survey Circular 1186, Denver, Colorado, 79 p.
Kazmann, R. G. (1956). "Safe yield" in ground water development: Reality or illusion?
Journal of the Irrigation and Drainage Division,
American Society of Civil Engineers, Vol. 82, No. IR3, November, Paper 1103.
Lee, C. H. (1915). The determination of safe yield of underground reservoirs of the closed-basin type. Transactions, American Society of Civil Engineers, Vol. LXXVIII, Paper No. 1315, 148-218.
L'vovich, M. I. 1979. World water resources and their future.
Translation from Russian by Raymond L. Nace, American Geophysical Union.
Ponce, V. M., and A. V. Shetty. 1995.
A conceptual model of catchment balance: 2. Application to runoff
and baseflow modeling.
Journal of Hydrology, 173, 41-50.
Ponce, V. M., R. P. Pandey, and S. Ercan. 2000. Characterization of drought across climatic spectrum.
Journal of Hydrologic Engineering, ASCE, Vol. 5, No. 2, April, 222-224.
Ponce, V. M. 2006. Groundwater utilization and sustainability. Online article.
Ponce, V. M. 2007. Sustainable yield of groundwater. Online article.
Ponce, V. M. 2014a.
Effect of groundwater pumping on the health of arid vegetative ecosystems. Online article.
Ponce, V. M. 2014b. Engineering hydrology: Principles and practices. Online textbook.
Ponce, V. M. and B. Vuppalapati. 2015.
The myth of groundwater resource evaluation. Online article.
Ponce, V. M. 2018.
Why is the cybernetic hydrologic balance
better suited for yield hydrology
than the conventional approach?
Online article.
Prudic, D. E., and M. E. Herman. 1996. Ground-water flow and simulated effects of development in Paradise Valley, a basin tributary to the Humboldt River, in Humboldt County, Nevada. U.S. Geological Survey Professional Paper 1409-F.
Sophocleous, M. 1997. Managing water resources systems: Why "safe yield" is not sustainable. Editorial,
Ground Water, Vol. 35, No. 4, July-August, 561.
Theis, C. V. 1940.
The source of water derived from wells: Essential factors controlling the response of an aquifer to
development.
Civil Engineering, Vol. 10, No. 5, May, 277-280.
|
| 240910 |