Fecho dos Morros, literally Closing of the Hills, a substantial tectonic uplift feature (≃ 40 m)
responsible for the existence of the mild land-surface slope (So ≃ 0.00001) and associated
runoff diffusion in the Pantanal of Mato Grosso, Mato Grosso do Sul, Brazil.


IS THE DYNAMIC HYDRAULIC DIFFUSIVITY ALTOGETHER

BETTER THAN ITS KINEMATIC COUNTERPART?


Victor M. Ponce

Professor of Civil and Environmental Engineering

San Diego State University, San Diego, California


23 October 2023

ABSTRACT. A comparison between kinematic and dynamic hydraulic diffusivities using an actual catchment model of overland flow is accomplished. The kinematic diffusivity is the well known Hayami diffusivity. On the other hand, the dynamic diffusivity is a function of the Vedernikov number. Several examples of rainfall-runoff conversions using the catchment model show that the difference between these two formulations of hydraulic diffusivity is negligible. This may be attributed to the very low Vedernikov numbers typically featured in catchment models, or to the specification of kinematic and diffusion waves in the test cases, since the latter are the only ones likely to be encountered in actual practice. The question of the true nature of mixed kinematic-dynamic waves is examined using available analytical data. It is concluded that given their extremely strong dissipative tendencies, mixed waves may not be there for us to calculate. Nevertheless, the dynamic hydraulic diffusivity is advocated as the method of choice, because it is the complete solution, it is applicable to all types of routing, and it does not significantly complicate the methodology.

1.  INTRODUCTION

Runoff diffusion is the property of free-surface flows to diffuse appreciably, attenuating unsteady flow stages in Nature's apparently determined quest to return the flow to its steady uniform condition. Diffusion is characterized by the coefficient of the second-order term of the partial differential equation governing the flow (Ponce, 2014a: Diffusion waves). This coefficient is commonly referred to as hydraulic diffusivity.

Since the 1950s, several mathematical expressions for hydraulic diffusivity have been developed as more information became available. Hayami (1951) developed the first expression for hydraulic diffusivity. He was followed by Dooge (1973) and later by Dooge and others (1982), culminating in the work of Ponce (1991), who identified the Vedernikov number in the expression for dynamic hydraulic diffusivity. The question remains as to whether the aforementioned improvements are indeed such when practical applications are considered. This article reviews and compares Hayami's and Ponce's expressions for hydraulic diffusivity. In the process, we manage to advertently cast a doubt on the existential nature of dynamic waves (Ponce, 2023a).

2.  KINEMATIC HYDRAULIC DIFFUSIVITY

Hayami (1951) pioneered the diffusion wave approach with free-surface flow (Ponce, 2023a) with the specific purpose for flood routing applications. His approach has been widely referred to in the literature as Hayami's diffusion analogy. He neglected the inertia terms in the equation of motion and combined the resulting equation with the equation of water continuity to derive a second-order equation with discharge as dependent variable. The coefficient of the second-order term, i.e., Hayami's hydraulic diffusivity, is (Ponce, 2014):

            qo
ν  =  _______
           2So 		(1)

in which ν = hydraulic diffusivity, qo = reference unit-width discharge, and So = bottom slope.

Since Hayami's formulation explicitly excludes inertia, it is properly a kinematic hydraulic diffusivity, to follow the work of Lighthill and Whitham (1955) on kinematic wave theory. Therefore:

             qo
νk  =  _______
            2So 		(2)

in which νk = kinematic hydraulic diffusivity.

3.  DYNAMIC HYDRAULIC DIFFUSIVITY

Using linear theory, Dooge (1973) derived the complete convection-diffusion equation of flood flows, including the inertia terms, leading to the formulation of a dynamic hydraulic diffusivity:

              qo                 F2
νd  =  _______  ( 1 - ______ )
             2So                4 		(3)

in which νd = dynamic hydraulic diffusivity. In Equation 3, F = Froude number of the equilibrium flow, defined as follows: F = v / (g D)1/2, in which v = mean flow velocity, g = gravitational acceleration, and D = hydraulic depth, defined as D = A / T, in which A = flow area, and T = channel top width.

Dooge and others (1982) improved the original Dooge formulation (Eq. 3) by expressing the fraction within parenthesis in terms of the exponent β of the discharge-flow area rating Q = α A β, to yield:

              qo                 
νd  =  _______  [ 1 - (β - 1)2 F2 ]
             2So                 		(4)

In fact, for Chezy friction in a hydraulically wide channel, β = 1.5. Therefore, for this case, Eq. 4 is shown to be equivalent to Eq. 3.

Ponce (1991a; 1991b) recognized the term  (β - 1)F  in Eq. 4 as the Vedernikov number V (Ponce, 2014b), thereby reducing the expression for dynamic hydraulic diffusivity to the following:

              qo                 
νd  =  _______  ( 1 - V2 )
             2So                 		(5)

We note that while the kinematic hydraulic diffusivity (Eq. 2) is independent of the Vedernikov number, the dynamic hydraulic diffusivity (Eq. 5) has a clearly defined threshold for V = 1, being positive for V < 1, leading to wave attenuation, and negative for V > 1, leading to wave amplification.

4.  TYPES OF WAVES IN OPEN-CHANNEL FLOW

While Equation 2 does not include the inertia terms, Equation 5 clearly does. Therefore, Eq. 5 should be a more accurate description of hydraulic diffusivity. To throw additional light on the issue, Table 1 shows the various types of waves in unsteady open-channel flow, including classical and common names.

Equation 2 was derived by Hayami by neglecting inertia in the equation of motion (Table 1, Line 2), i.e., a kinematic wave with diffusion; therefore, we confirm the appropriateness of the name kinematic hydraulic diffusivity. On the other hand, Eq. 5 was derived by considering all terms in the equation of motion (Table 1, Line 4), i.e., a mixed kinematic-dynamic wave, commonly referred to as a dynamic wave; therefore, the name dynamic hydraulic diffusivity appears justified at this juncture.

Table 1.  Types of waves in unsteady open-channel flow.
Line No. Classical wave name Terms included in the equation of motion Common name
Local inertia Convective inertia Pressure gradient Friction Gravity
1 Kinematic       ✓ ✓ Kinematic
2 Kinematic with
diffusion 		    ✓ ✓ ✓ Diffusion
3 Dynamic ✓ ✓ ✓     "Gravity"
4 Mixed kinematic-
dynamic 		✓ ✓ ✓ ✓ ✓ "Dynamic"

We have confirmed that Eq. 2 is an approximation for hydraulic diffusivity and that Eq. 5 is the complete expression. The question arises as to what is the actual difference between the two formulations when practical applications are considered. In the following section (Section 5) we evaluate the difference between the two alternative formulations for hydraulic diffusivity (Eqs. 2 and 5) using a catchment model of overland flow.

5.  COMPARISON BETWEEN DIFFUSIVITIES

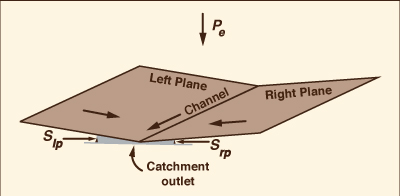
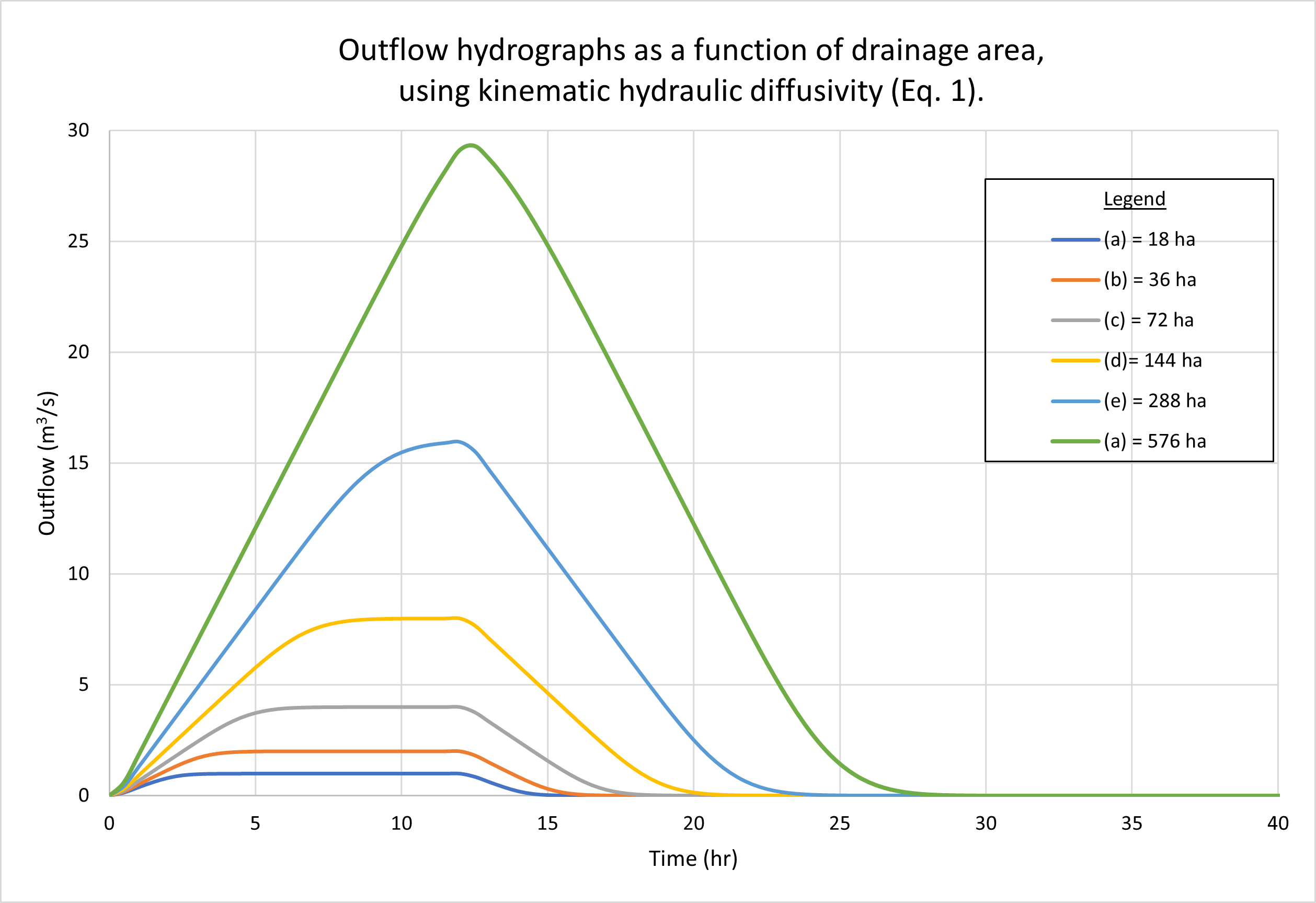
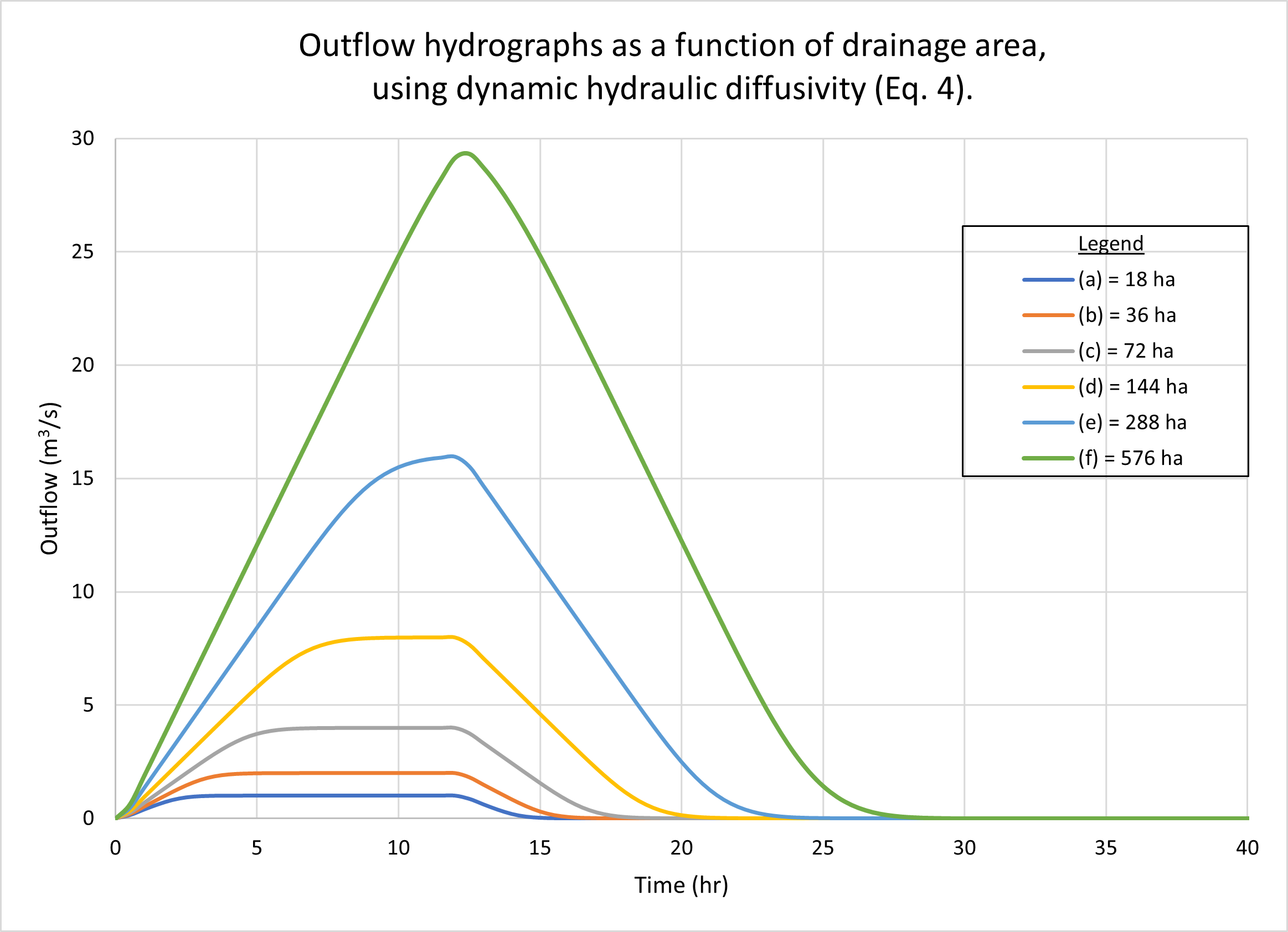
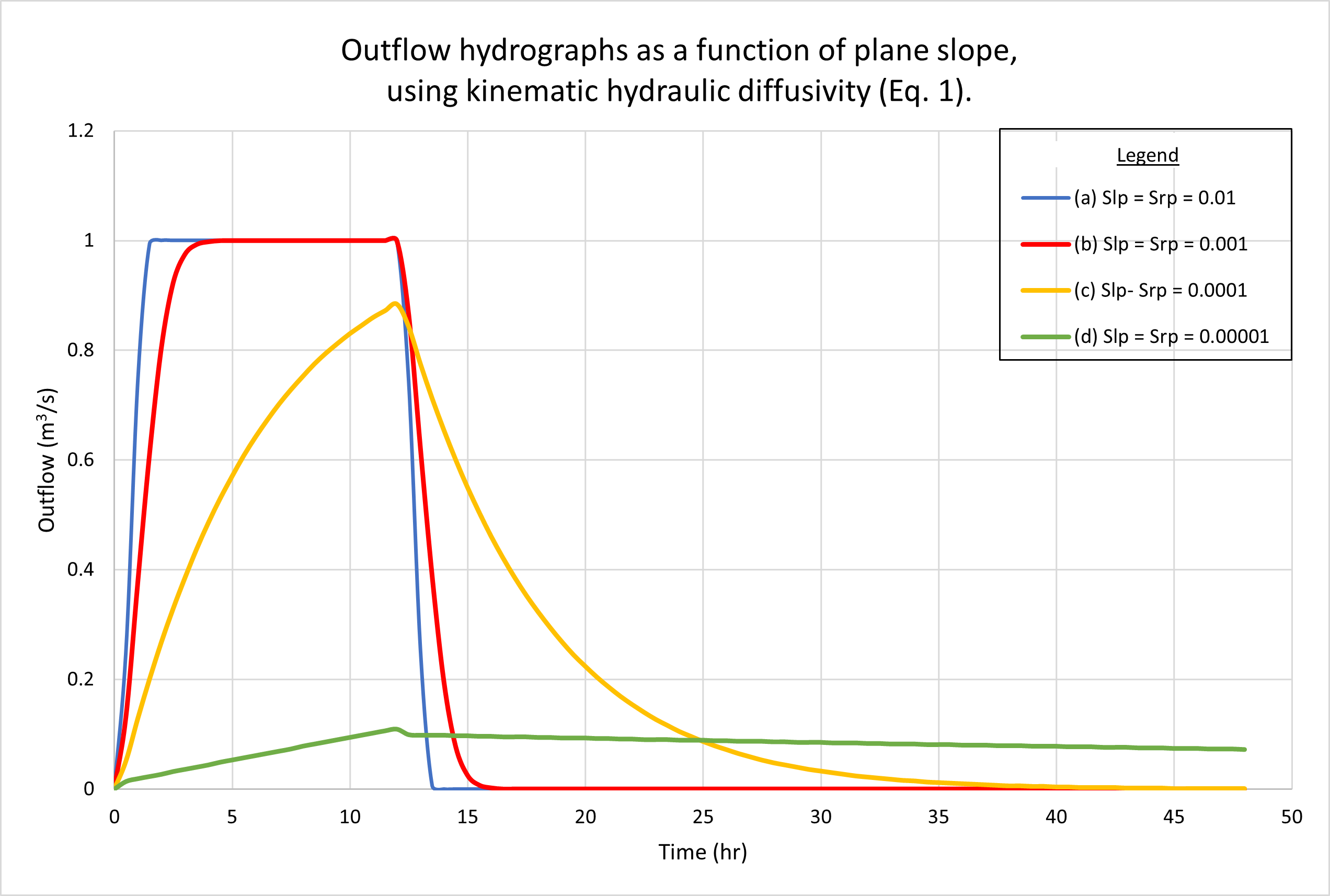
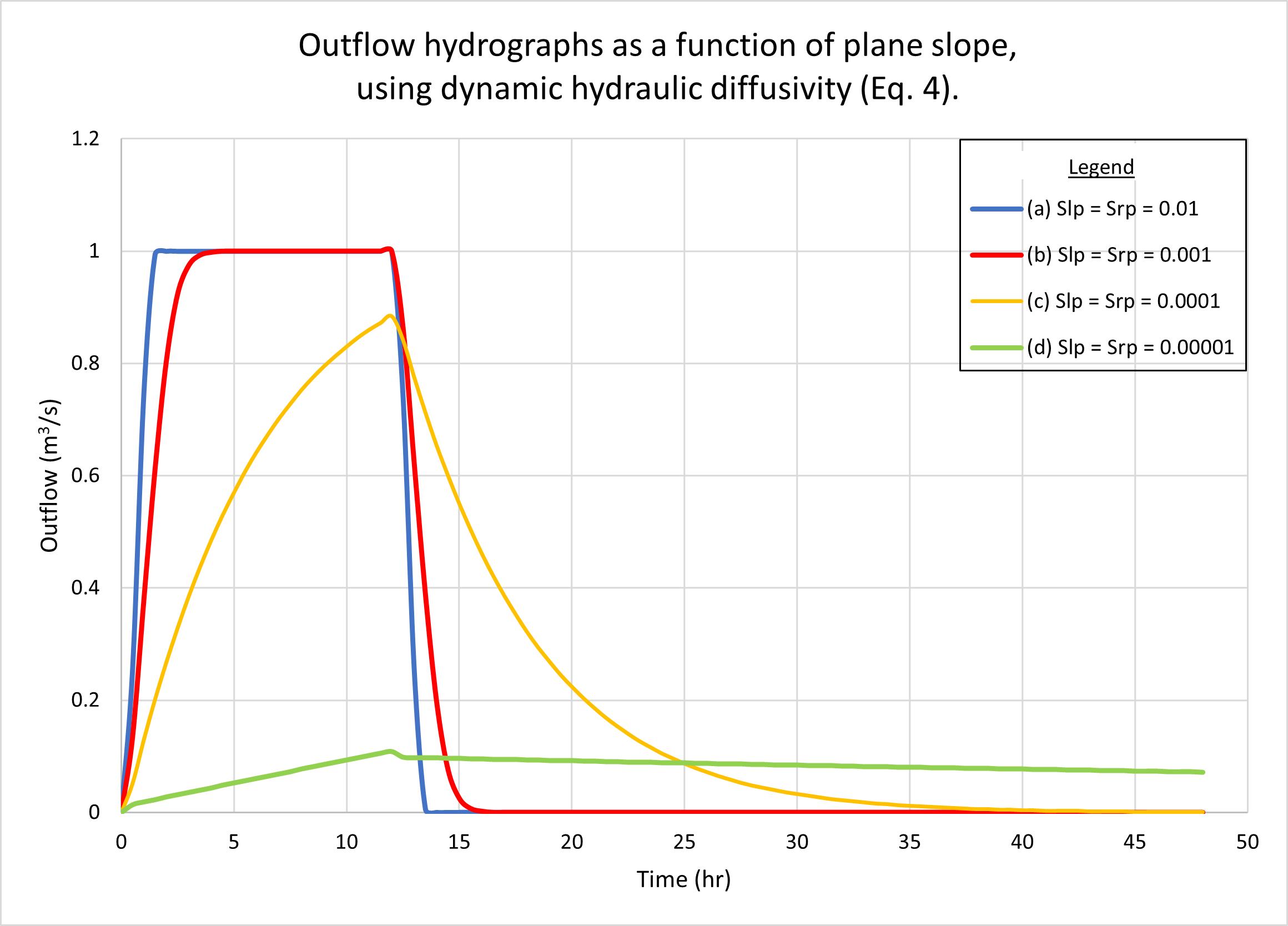
In this section, we use an overland flow model to test the difference between the two formulations of hydraulic diffusivity, Eqs. 2 and 5. The model simulates catchment dynamics using an open-book geometric configuration, i.e., two planes (left and right) and one channel in the middle (Fig. 1) (Ponce, 1986). The model's rainfall-runoff results are compared for the following two conditions: (1) kinematic hydraulic diffusivity (Eq. 2); and (2) dynamic hydraulic diffusivity (Eq. 5) (Ponce and Scott, 2022).

Fig. 1  ONLINEOVERLAND open-book geometric configuration.

The results show negligible differences between the two diffusivities under a wide range of flow conditions. Kinematic waves (Table 1, Line 1) and diffusion waves (Table 1, Line 2) were used in the tests because these were the only ones likely to be encountered in actual practice. The Vedernikov number in the planes was quite low, around 0.03.

Figure 2 shows the outflow hydrographs for drainage areas varying from 18 hectares (small) to 576 hectares (midsize). Figure 3 shows the outflow hydrographs for plane slopes (left and right) varying from 0.01 (steep) to 0.00001 (mild). No appreciable differences are observed between hydrographs generated using kinematic [(a) figures] and dynamic [(b) figures] hydraulic diffusivities.

[Click on top of figure to expand]

Fig. 2 (a)  Outflow hydrographs as a function
of drainage area using kinematic
hydraulic diffusivity.
[Click on top of figure to expand]

Fig. 2 (b)  Outflow hydrographs as a function
of drainage area using dynamic
hydraulic diffusivity.

[Click on top of figure to expand]

Fig. 3 (a)  Outlow hydrographs as a function
of plane slope using kinematic
hydraulic diffusivity.
[Click on top of figure to expand]

Fig. 3 (b)  Outlow hydrographs as a function
of plane slope using dynamic
hydraulic diffusivity.

The lack of any appreciable difference between output hydrographs when comparing results using kinematic and dynamic diffusivities (Eqs. 2 and 5) is attributed to the type of modeling used in this study. Catchment flow typically features low Vedernikov numbers, particularly in the planes; in this case, V ≃ 0.03. In fact, for V = 0.03: νd = 0.9991 νk.

The examples shown in Figs 2 and 3 depict kinematic waves (Table 1, Line 1) and diffusion waves (Table 1, Line 2), since these are the ones likely to be encountered in actual practice. By definition, these waves are not subject to substantial diffusion; thus, featuring relative small values of either of the two diffusivities. We conclude that when modeling catchment flows using kinematic and diffusion waves, the difference between hydraulic diffusivities is likely to be negligible.

6.  DOES THE DYNAMIC WAVE REALLY EXIST IN PRACTICE?

A question to be addressed at this juncture is the nature of mixed kinematic-dynamic waves (Table 1, Line 4), the so-called "dynamic" waves of hydraulic engineering (Fread, 1985). Do the dynamic waves really exist in practice? It is appropriate to begin this discussion with a quote from Lighthill and Whitham (1955), who, in their seminal treatise on kinematic waves, saw fit to describe the dynamic waves as follows.

"... In some applications, including the case of flood waves, kinematic waves and dynamic waves are both possible together. However, the dynamic waves have both a much higher wave velocity and also a rapid attenuation. Hence, although any disturbance sends some signal downstream at the ordinary wave velocity for long gravity waves, this signal is too weak to be noticed at any considerable distance downstream, and the main signal arrives in the form of a kinematic wave at a much slower speed." (Page 285).

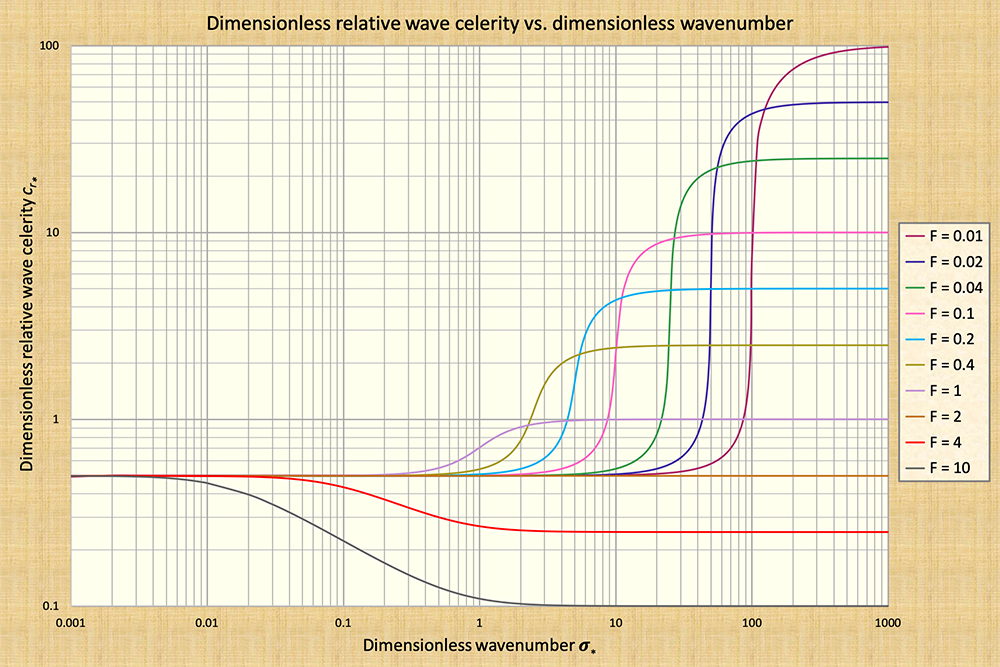
Further confirmation of the correctness of Lighthill and Whitham's observations regarding the strong dissipative nature of dynamic waves was given by Ponce and Simons (1977), who used linear stability analysis to derive celerity and attenuation functions for the four types of shallow-water waves shown in Table 1. Ponce and Simons (1977) identified the dimensionless wavenumber σ* as the fundamental physical parameter describing the propagation of shallow-water waves. Their findings are summarized in Fig. 4.

The amount of wave diffusion is expressed in terms of the logarithmic decrement δ, a measure of the rate at which the wave changes upon propagation (Wylie, 1966). The definition of logarithmic decrement is: δ = ln Q1 - ln Q0, or, alternatively: Q1 = Q0 eδ, in which Q0 = flood discharge at the start of the measurement, and Q1 = flood discharge after an elapsed time equal to one (sinusoidal) period of propagation.

[Click on top of figure to expand]

Fig. 4 (a)  Dimensionless relative celerity vs dimensionless wavenumber in unsteady open-channel flow.
[Click on top of figure to expand]

Fig. 4 (b)  Logarithmic decrement vs dimensionless wavenumber in unsteady open-channel flow.

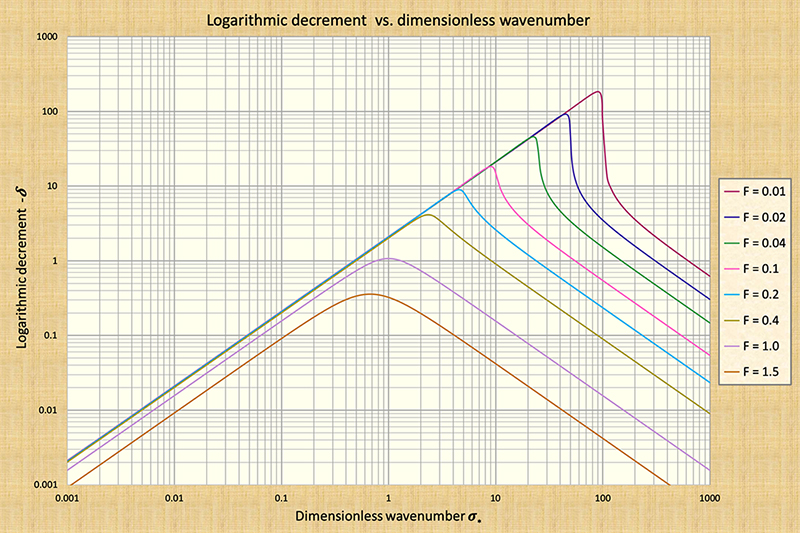
The findings of Ponce and Simons (1977) confirm the very strong dissipative tendencies of mixed kinematic-dynamic waves, commonly referred to in the hydraulic engineering literature simply as "dynamic waves" (Fread, 1985). The peak attenuation amount occurs at the point of inflection in the dimensionless relative celerity cr* vs dimensionless wavenumber σ* [compare Fig. 4 (a) with Fig. 4 (b)]. Note that the amount of wave attenuation increases markedly with a decrease in equilibrium flow Froude number. For the lowest Froude number shown in Fig. 4, F = 0.01, the peak logarithmic decrement is δ = 180, corresponding to σ* = 90 [Fig. 4 (b)].

Table 2 shows peak logarithmic decrements (Column 3) for the range of subcritical Froude numbers between 0.01 and 1.5 (Column 1) shown in Fig. 4 (b) and their corresponding wave attenuation amounts (Column 5). The prevailing wave type is shown to be mixed kinematic-dynamic for all subcritical flows, and kinematic with diffusion for critical and supercritical flows (Column 6). The amount of wave attenuation, shown at or very close to 1, indicates that the entire range of subcritical flows is subject to very strong dissipative tendencies. This result further casts doubts on the mixed kinematic-dynamic wave as a basis for computation. The mixed kinematic-dynamic wave is simply not there for us to calculate!

Table 2. Peak logarithmic decrements of the mixed kinematic-dynamic wave model
for Froude numbers between F = 0.01 and F = 1.5.
[1] [2] [3] [4] [5] [6]
Froude No. Dimensionless wavenumber σ* Peak logarithmic decrement δeδWave attenuation
(1 - eδd)		Wave type
0.01901800.1.Mixed kinematic-dynamic
0.0245950.1.Mixed kinematic-dynamic
0.0423480.1.Mixed kinematic-dynamic
0.19190.1.Mixed kinematic-dynamic
0.24.59.50.1.Mixed kinematic-dynamic
0.42.34.20.0150.985Mixed kinematic-dynamic
1.01.11.10.3330.667Kinematic with diffusion
1.50.70.370.6910.309Kinematic with diffusion

Having demonstrated that the mixed kinematic-dynamic wave may not be there for us, we still have a choice of using or not the dynamic hydraulic diffusivity (Eq. 5) in all applications of unsteady free-surface flow, including both catchment and channel flow. Since Eq. 5 is indeed the complete equation to model diffusivity and it does not significantly complicate the calculation of runoff diffusion it may still be regarded as the best choice.

7.  SUMMARY

A comparison between kinematic and dynamic hydraulic diffusivities using an actual catchment model of overland flow is accomplished. The kinematic hydraulic diffusivity is the well known Hayami diffusivity, which is independent of the Vedernikov number. On the other hand, the dynamic hydraulic diffusivity is a function of the Vedernikov number. Several examples of rainfall-runoff conversions using the catchment model show that the difference between these two formulations of hydraulic diffusivity is negligible. This may be attributed to the very low Vedernikov numbers typically featured in catchment models, or to the specification of kinematic and diffusion waves in the test cases, since these waves are the only ones likely to be encountered in actual practice.

The question of the true nature of mixed kinematic-dynamic waves is examined using available analytical data. It is concluded that given their extremely strong dissipative tendencies, mixed waves may not be there for us to calculate. Nevertheless, the dynamic hydraulic diffusivity is advocated as the method of choice because it is the complete solution, it is applicable to all types of routing, including catchment and channel flow, and it does not significantly complicate the methodology.

REFERENCES

Dooge, J. C. I. 1973. Linear theory of hydrologic systems: Lecture 9. Technical Bulletin No. 1468, U.S. Department of Agriculture, Washington, D.C. Dooge (1973).

Dooge, J. C. I., W. B. Strupczewski, and J. J. Napiorkoswki. 1982. Hydrodynamic derivation of storage parameters in the Muskingum model. Journal of Hydrology, 54, 371-387.

Fread, D. L. 1985. "Channel Routing," in Hydrological Forecasting, M. G. Anderson and T. P. Burt, eds. New York: John Wiley.

Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, December.

Lighthill, M. J. and G. B. Whitham. 1955. On kinematic waves. I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.

Natural Resources Conservation Service (NRCS). 1985. National Engineering Handbook. Section 4: Hydrology, Washington, D.C. (First edition: 1954).

Ponce, V. M. and D. B. Simons. 1977. Shallow wave propagation in open channel flow. Journal of Hydraulic Engineering, ASCE, 103(12), 1461-1476.

Ponce, V. M. 1986. Diffusion wave modeling of catchment dynamics. Journal of Hydraulic Engineering, Vol. 112, No. 8, August, 716-727.

Ponce, V. M. 1991a. The kinematic wave controversy. Journal of Hydraulic Engineering, Vol. 117, No. 4, April, 511-525.

Ponce, V. M. 1991b. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.

Ponce, V. M. 2014a. Engineering Hydrology: Principles and Practices. Online textbook.
https://ponce.sdsu.edu/enghydro/index.html

Ponce, V. M. 2014b. Fundamentals of Open-channel Hydraulics. Online textbook.
https://ponce.sdsu.edu/openchannel/index.html

Ponce, V. M. and A. C. Scott. 2022. Comparison between kinematic and dynamic hydraulic diffusivitites using script ONLINEOVERLAND. Online paper.

Ponce, V. M. 2023a. When is the diffusion wave applicable? Online paper.

Ponce, V. M. 2023b. Kinematic and dynamic waves: The definitive statement. Online paper.

Wylie, C. R. 1966. Advanced Engineering Mathematics, 3rd ed., McGraw-Hill Book Co., New York, NY.

231023