Kinematic waves demystified, Victor M. Ponce

Fig. 1 Upper Paraguay river at Porto Murtinho, Mato Grosso do Sul, Brazil,
featuring a flood hydrograph lasting one year (the maximum possible),
clearly the quintessential kinematic flood wave.

KINEMATIC WAVES DEMYSTIFIED

Victor M. Ponce

Professor Emeritus of Civil and Environmental Engineering

San Diego State University, San Diego, California

21 March 2024

ABSTRACT. We have clarified the concept of kinematic wave and its applications in hydraulic and hydrologic engineering. We have focused on the nature of kinematic waves and its importance as the method of choice for modeling flood waves. Given the kinematic wave's capability to properly account for wave diffusion, its applicability is seen to be substantially enhanced. Competing wave types such as the mixed kinematic-dynamic and the dynamic waves of Lagrange lack either the size (scale) and/or permanence of kinematic waves. Therefore, the kinematic wave is regarded as the preferred method to model flood wave propagation.

1. INTRODUCTION

Kinematic waves remain clouded in controversy (Ponce, 1991). While they have been used in theory and practice for nearly six decades (since the 1960's), their advantages and disadvantages are often not completely understood by practitioners. Accordingly, our objective here is to shed additional light on the subject of kinematic waves, explaining their origin, nature, features, and utility. We round up the treatment by elaborating on ways to model kinematic waves properly and accurately.

2. ORIGIN OF KINEMATIC WAVES

The theoretical foundations of what we presently know as kinematic waves originated in the seminal work of Lighthill and Whitham (1955), who mathematically formulated a certain type of wave motions which ostensibly were not dynamic in nature. Rather, these waves could readily be construed as kinematic, since they followed purposely from the continuity equation of one-dimensional fluid motion. Furthermore, unlike dynamic waves, which are characteristically poised to transport energy, kinematic waves are actually transporting mass. Different terms in the governing equations describe each of these two waves, kinematic and dynamic; thus, their wave properties (celerity and attenuation) differ accordingly (Ponce and Simons, 1977).

Boussinesq (1877) mentions Breton (1867) and Graëff (1875) as pioneers of the theory. Chow (1959) credits Kleitz (1877) with being the first to derive the formula for the celerity of a kinematic wave. A few years later, Seddon (1900) evaluated the said celerity from actual gage measurements in the Mississippi and Missouri rivers. Following a detailed analysis, Seddon concluded that the celerity m of a kinematic wave at a given cross-section is equal to the slope dQ/dh of the applicable rating curve, divided by its width W. In practice, Seddon's formula for the kinematic wave celerity has been referred to as the Kleitz-Seddon law, or simply as Seddon's law. More than 50 years later, Seddon's findings were amply confirmed by Lighthill and Whitham (1955).

3. NATURE OF KINEMATIC WAVES

Kinematic waves are flood waves; the reverse statement is also true: Flood waves are kinematic; albeit with some exceptions which we will discuss in Section 5. Lighthill and Whitham (1955) put it clearly when they stated, to wit: "In some applications, including the case of flood waves, kinematic waves and dynamic waves are both possible together. However, the dynamic waves have a much higher wave velocity and also a rapid attenuation. Hence, although any disturbance sends some signal downstream at the ordinary wave velocity for long gravity waves [sic], this signal is too weak to be noticed at any considerable distance downstream, and the main signal arrives in the form of a kinematic wave at a much slower velocity." Thus, in many problems of practical interest, the dynamic waves are seen to be completely subordinated to the kinematic waves, which travel downstream only, with significantly greater mass and volume, and at a much slower speed (celerity).

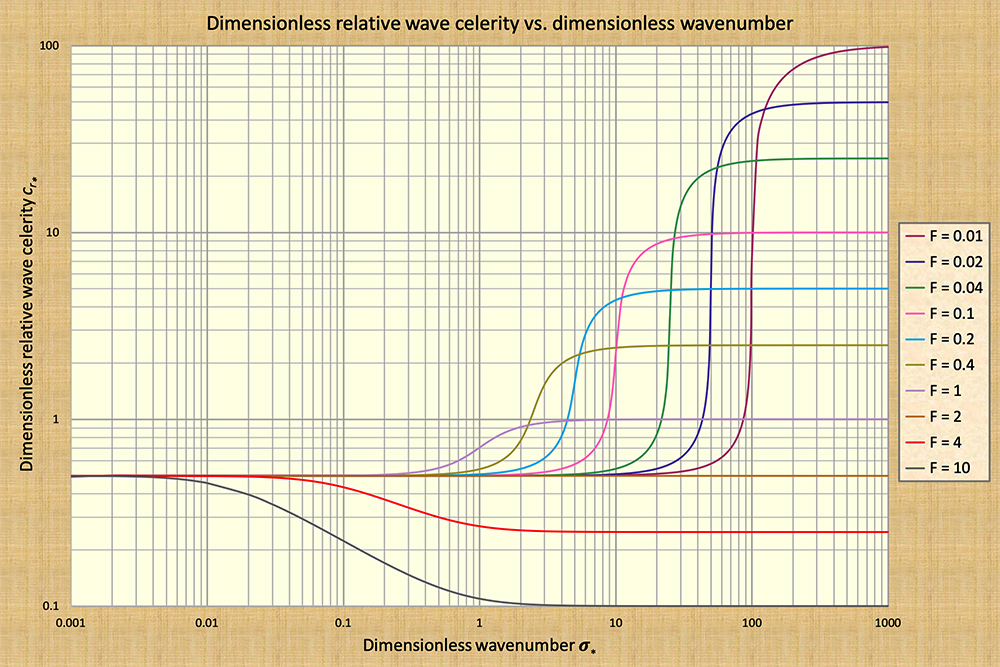
The differences between the various types of waves in one-dimensional open-channel flow has been clarified by Ponce and Simons (1977). They used linear stability theory to determine celerity and attenuation functions for all types of shallow-water waves, including: (1) kinematic, (2) mixed kinematic-dynamic, and (3) dynamic. The unifying element is seen to be the dimensionless wavenumber σ_{_*}, defined by multiplying the applicable wavenumber (2π /L) times the reference channel length L_o, i.e., the length of channel that it would take the equilibrium flow to drop a head equal to its depth.

Kinematic waves are those of Seddon (1900), while dynamic waves are those of Lagrange (1877) [Note that the latter are the "long gravity waves" referred to by Lighthill and Whitham; see the previous paragraph]. Mixed kinematic-dynamic waves are those lying along the middle-to-right of the wavenumber spectrum identified by Ponce and Simons (1977) (Fig. 2). These "mixed" waves were featured in the numerical models developed beginning in the 1970s to solve the complete St. Venant equations (Fread, 1985). These models have been widely referred to as "dynamic wave" models although the misnomer has led to confusion with the classical Lagrange (1877) waves.

Ponce and Simons (1977)

Fig. 2 Dimensionless relative wave celerity c_{_{_r}}_{_{_*}} vs dimensionless wavenumber σ_{_{_*}}.

To put it in a nutshell, Seddon's kinematic waves, lying toward the left of the dimensionless wavenumber spectrum, feature a constant wave celerity and are, therefore, nondiffusive. Following the same rationale, Lagrange's dynamic waves, lying toward the right, are also nondiffusive. However, the mixed kinematic-dynamic waves, lying toward the middle-to-right and featuring sharply varying celerity, are shown to be strongly diffusive! The amount of diffusion varies with the prevailing Froude number, with greater diffusion corresponding to the lower Froude numbers, provided the latter remains below the threshold value F = 2, applicable for Chezy friction in hydraulically wide channels (Fig. 2).

To close, we reiterate that Lighthill and Whitham (1955) pointedly elaborated on the competition between kinematic and mixed waves, in order to show how completely the latter are subordinated to the former in the case of greatest practical interest, that is, when the speed of the river is well below subcritical. This underscores the general unsuitability of the mixed wave as a basis for flood wave computations and, by extension, stresses the practical importance of kinematic waves.

4. KINEMATIC-WITH-DIFFUSION WAVES

And here is where the plot tickens! Kinematic waves are referred to as such because they occur ostensibly in the absence of inertia, while also excluding the pressure gradient [Table 1, Row 1]. Conversely, the (exact opposite, to judge by its components) dynamic wave occurs significantly in the absence of only friction and gravity [Row 4].

Note that the existence of the pressure-gradient term complicates the definition of kinematic waves. This fact led Lighthill and Whitham (1955) to distinguish between two types of kinematic waves: (1) those with friction and gravity only, excluding inertia and the pressure gradient, referred to simply as kinematic waves [Row 1]; and (2) those with friction, gravity and the pressure gradient, excluding only inertia, referred to as kinematic-with-diffusion waves or, for short, diffusion waves [Row 2] (Ponce and Simons, 1977). The mixed kinematic-dynamic waves, which feature all terms in the equation of motion [Row 3], complete the list of shallow-water waves in hydraulic engineering practice.

Table 1. Types of waves in unsteady open-channel flow.
No.	Wave name	Terms of the equation of motion participating in the wave description					Common name
No.	Wave name	Local inertia	Convective inertia	Pressure gradient	Friction	Gravity	Common name
1	Kinematic				✓	✓	Kinematic
2	Kinematic-with-diffusion			✓	✓	✓	Diffusion
3	Mixed kinematic-dynamic	✓	✓	✓	✓	✓	Mixed
4	Dynamic (Lagrange)	✓	✓	✓			Dynamic

We observe that since kinematic waves do not attenuate [Row 1], and diffusion waves do [Row 2], it follows that the pressure-gradient term must be responsible for the attenuation, i.e., the limited amount of wave diffusion experienced by typical flood waves. That this is, indeed, the case has been amply confirmed by theory and practice.

We have established that dynamic (Lagrange) waves [Row 4] are too small to resemble flood waves. We have also established that mixed kinematic-dynamic waves [Row 3] are too dissipative to play a practical role in flood wave applications. Therefore, only kinematic [Row 1] and diffusion [Row 2] waves are likely to be large enough, and permanent enough, to be appropriate models of flood wave propagation.

The precise amounts of flood wave diffusion, shown in Table 2, have been calculated by Ponce (2023a). For this purpose, the range of applicable dimensionless wavenumbers varies five orders of magnitude, from σ_{_{_*}} = 0.0001 to σ_{_{_*}} = 10 (Fig. 2). For σ_{_{_*}} = 0.0001, the waves are kinematic, undergoing zero attenuation; for σ_{_{_*}} = 0.001, the waves are kinematic to diffusion, undergoing very little attenuation (0.002); for σ_{_{_*}} = 0.01, the waves are diffusion, undergoing small but perceptible attenuation (0.021); for σ_{_{_*}} = 0.1, the waves are definitely diffusion, undergoing sizable attenuation (0.189); for σ_{_{_*}} = 1, the waves are mixed, undergoing very strong attenuation (0.877); and for σ_{_{_*}} = 10, the waves have completely attenuated (1.0), i.e., they have ceased to exist!

Table 2. Amounts of wave diffusion across the dimensionless wavenumber spectrum.
[1]	[2]	[3]	[4]	[5]	[6]
No.	*Dimensionless wavenumber σ_{_{_}}**	Logarithmic decrement δ_d	e^δ_d	Wave attenuation (1 - e^δ_d)	Wave type
0	0.0001	0.00020944	1	0	Kinematic
1	0.001	0.0020944	0.998	0.002	Kinematic to diffusion
2	0.01	0.020944	0.979	0.021	Diffusion
3	0.1	0.20944	0.811	0.189	Diffusion
3a	0.17	0.35604	0.700	0.300	Diffusion to mixed
4	1	2.0944	0.123	0.877	Mixed
5	10.	20.944	0	1.0	Mixed

We confirm that kinematic waves are not subject to attenuation, although they may undergo change of shape due to nonlinearities (Ponce and Windingland, 1985). We also confirm that for the midrange value of dimensionless wavenumber σ_{_{_*}} > 0.17, the wave attenuation is greater than 0.30 (30%), a threshold which is widely regarded as the limit between diffusion waves (of limited wave diffusion, less than 30%) and mixed waves (of unlimited wave diffusion, which could reach 1.0 (100%) (Flood Studies Report, 1975). Therefore, it is confirmed that mixed waves are very strongly dissipative and, in most cases of practical interest, they are not likely to be there for us to calculate them (Ponce, 1992).

Before we wrap up the subject of kinematic waves vis-à-vis flood waves, it remains for us to bring into the proper context the nature of roll waves. Are these waves kinematic or dynamic? It has now been firmly established that roll waves occur in steep lined channels of rectangular cross-section when the kinematic wave celerity (Seddon celerity) exceeds the dynamic wave celerity (Lagrange celerity) (Craya, 1952). In unsteady open-channel flow, this condition exists when the Vedernikov number exceeds the threshold V = 1, typically in steep lined of rectangular cross-section (Ponce, 1991b). Note that this condition is equivalent to a Froude number F = 2, applicable to Chezy friction in hydraulically wide channels.

The question as to whether a roll-wave event may be considered a flood wave is an assessment that is best left to the individual case. If the roll waves manage to overcome the channel boundaries, they may be considered dangerous and, therefore, a flood wave "of sorts". Otherwise, if the roll waves remain constrained within the channel boundaries, within reason, they may not be taken as flood waves. The flood risk arising from a roll-wave event tends to be highly site-specific, with recurrent determinations likely to vary in space and time.

To close, we affirm that kinematic and diffusion waves find their practical application in the routing of flood waves. Flood waves are generally massive and slow moving, unlike dynamic (Lagrange) waves that are neither. Furthermore, mixed waves are so diffusive that they quickly disappear, with their mass going on to join the adjacent or underlying kinematic waves, which continue to grow as they propagate downstream.

5. USES OF KINEMATIC AND DIFFUSION WAVES

Kinematic waves find their best application in the routing of flood waves. However, they have also been used in the routing of free-surface (overland) flows, which, due to their usually reduced scale, may not constitute actual flood waves. Wooding (1965) was the first to apply kinematic flow in numerical (digital computer) models of overland flow, using an open-book configuration which has been widely referred to as the Wooding plane (Fig. 2).

Fig. 2 The Wooding plane: Open-book geometric configuration used in the modeling of free-surface overland flow.

The most general application of kinematic waves is in the routing of flood waves, that is, the numerical computer calculation of the progression of a flood wave as it travels downstream, along a stream, river, or channel. The actual flood wave may be a kinematic wave, with zero diffusion or, else, a diffusion wave, featuring a small but perceptible amount of diffusion, i.e., wave attenuation or dissipation (Table 2). Flood waves are thus formed as the agglomeration of an infinite number of mixed waves of varying sizes, with their strong diffusive tendencies acting to convert the relatively small-scale mixed waves into a much larger kinematic or diffusion flood wave (Lighthill and Whitham, 1955).

The distinguishing property of flood waves is that they are generally massive, and that they have little or no attenuation. In an actual field situation, the contributions of lateral inflows, from all sources, will ensure that flood waves continue to increase in mass and overall size, becoming more massive and, therefore, less attenuating, as the flood wave progresses downstream.

Numerical computer models of kinematic and diffusion waves are in current use. They have been around since the 1970s, but they are not without pitfalls. Analytical solutions of the kinematic wave equation lack diffusion; numerical solutions, however, will invariably show a perceptible amount of diffusion. The latter must be attributed to the diffusion originating in the numerical scheme itself, since diffusion is absent in the (analytical) kinematic wave equation. Schemes that rely on the kinematic wave equation have no way of relating the observed numerical diffusion to the actual physical diffusion of the problem at hand (U.S. Army Corps of Engineers, 2024). Therefore, they are conceptual at best, generally falling short of the accuracy that would be expected in a mathematical model that is truly physically based.

The dilemma has been resolved by Cunge (1969), who proposed a match of the numerical diffusion of the scheme itself with the physical diffusion of the related kinematic wave equation with diffusion, i.e., the diffusion wave equation. This development led to the Muskingum-Cunge method of flood routing (Ponce, 2014), an improvement on the classical Muskingum method of McCarthy (1938).

The feature of grid independence, a significant asset of the Muskingum-Cunge method, sets it apart from methods based solely on the kinematic wave equation (Ponce, 1986; Ponce, 2023b). Therefore, overland flow models with diffusion wave components are clearly the next step in catchment, watershed and basin modeling (Aguilar, 2014).

6. A SINGULAR EXAMPLE

By now, surely the reader may have become thoroughly familiar with the nature and utility of kinematic waves, and, by extension, of diffusion waves. All flood waves worthy of the name are subject to modeling using kinematic wave theory. It should be obvious that the greater the basin, the more kinematic the wave is, and the more damage may be caused by an associated flood. Kinematic waves are not only large, but are also slowly decaying, or attenuating, and in some cases, they lack attenuation completely (See Table 2, Row 0). No wonder researchers like Seddon (1900) were able to document only kinematic waves in their pioneering work. We reckon that Lighthill and Whitham (1955) were very timely in expounding on kinematic wave theory, which widely facilitated ensuing research. Unfortunately, the title of their paper may be somewhat misleading: It read "Flood movement in long rivers." Instead, maybe it should have read: "Flood movement in all rivers".

We close by focusing on the example of the anual flood wave on the Upper Paraguay river, which drains 496,000 square kilometers in the plains of Western Central Brazil and Eastern Bolivia. The central portion of the basin drains a continental delta, with very mild stream and river bottom slopes, documented to be as low as 0.00001, or 1 cm/km. The resulting kinematic wave is so large that the flood wave measured at Porto Murtinho, Mato Grosso do Sul, has typically only one annual peak, basically constituting "the quintessential kinematic flood wave" (Fig.3).

Fig. 3 Upper Paraguay river at Porto Murtinho, Mato Grosso do Sul, Brazil,
featuring a flood hydrograph lasting typically one year.

7. CONCLUDING REMARKS

We have clarified the concept of kinematic wave and its applications in hydraulic and hydrologic engineering. We have focused on the nature of kinematic waves and its importance as the method of choice for modeling flood waves. Given the kinematic wave's capability to properly account for wave diffusion, its applicability is seen to be substantially enhanced. Competing wave types such as the mixed kinematic-dynamic and the dynamic waves of Lagrange lack either the size (scale) and/or permanence of kinematic waves. Therefore, the kinematic wave is regarded as the preferred method to model flood wave propagation.

REFERENCES

Aguilar, R. 2014. Diffusion wave modeling of catchment dynamics using online calculation. M.S. thesis, Departament of Civil, Construction, and Environmental Engineering, San Diego State University, San Diego, California, Spring.

Boussinesq. J. 1877. Essai sur la théorie de eaux courantes (Essay on the theory of running waters), Mém. prés. Acad.Sci., Paris, 23.

Breton, Ph. 1867. Sur les barrages de retenue des graviers dans les gorges des torrents (On gravel retention dams in torrent gorges), Paris.

Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, New York, NY.

Craya, A. 1952. The criterion for the possibility of roll wave formation. Gravity Waves, National Bureau of Standards Circular No. 521, National Bureau of Standards, Washington, D.C. 141-151.

Cunge, J. A. 1969. On the Subject of a Flood Propagation Computation Method (Muskingum Method). Journal of Hydraulic Research, 7(2), 205-230.

Flood Studies Report. 1975. Vol. III: Flood Routing Studies, Natural Environment Research Council, London, England.

Fread, D. L. 1985. "Channel Routing," in Hydrological Forecasting, M. G. Anderson and T. P. Burt, eds., Wiley, New York.

Graëff, J. 1875. Sur l'application des courbes de débits à l'etude du regime des rivières (On the application of flow curves to the study of the regime of rivers), Mém. prés. Acad.Sci., Paris, 21.

Kleitz, M. 1877. Note sur la théorie du mouvement non permanent des liquides et sur application à la propagation des crues des rivières (Note on the theory of unsteady flow of liquids and on application to flood propagation in rivers), Annales des ponts et chaussées, ser. 5, Vol. 16, 2e semestre, 133-196.

Lagrange, J. L. de. 1788. M�canique analytique, Paris, part 2, section II, article 2, 192.

Lighthill, M. J. and G. B. Whitham. 1955. On kinematic waves. I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.

McCarthy, G.T. . 1938. "The Unit Hydrograph and Flood Routing," unpublished manuscript, presented at a Conference of the North Atlantic Division, U.S. Army Corps of Engineers, June 24. (Cited by V. T, Chow's text "Open-channel Hydraulics," page 607).

Ponce, V. M. and D. B. Simons. 1977. Shallow wave propagation in open channel flow. Journal of Hydraulic Engineering, ASCE, 103(12), 1461-1476.

Ponce, V. N., and D. Windingland. 1985. Kinematic shock: Sensitivity analysis. Journal of Hydraulic Engineering, ASCE, 111(4), April, 600-611.

Ponce, V. M. 1986. Diffusion wave modeling of catchment dynamics. Journal of Hydraulic Engineering, 112(8), August, 716-727.

Ponce, V. M. 1991a. The kinematic wave controversy. Journal of Hydraulic Engineering, 117(4), April, 511-525.

Ponce, V. M. 1991b. New perspective on the Vedernikov number. Water Resources Research, 27(7), July, 1777-1779.

Ponce, V. M. 1992. Kinematic wave modeling: Where do we go from here? International Symposium on Hydrology of Mountainous Areas, Shimla, India, May 28-30.

Ponce, V. M. 2014. Engineering Hydrology: Principles and Practices. Online textbook.
https://ponce.sdsu.edu/enghydro/index.html

Ponce, V. M. 2023a. When is the diffusion wave applicable? Online publication.

Ponce, V. M. 2023b. Why is the Muskingum-Cunge the best flood routing method? Online publication.

Seddon, J. A. 1900. River Hydraulics. Transactions, American Society of Civil Engineers, Vol. XLIII, 179-243, June; Extract: pages 218-223.

U.S. Army Corps of Engineers. 2024. HEC-HMS Technical Reference Manual: Synopsis of Program Methods.
https://www.hec.usace.army.mil/confluence/hmsdocs/hmstrm/program-components/synopsis-of-program-methods>

Wooding, J. 1965. "A Hydraulic Model for the Catchment-stream Problem, I. Kinematic Wave Theory," Journal of Hydrology, Vol. 3, Nos. 3/4, 254-267.

240321