|
CAPÍTULO 2: PROPRIEDADES DE CANAIS |
2.1 TIPOS DE CANAIS
|
|
Em geral, existem dois tipos de canais abertos: (1) natural e (2) artificial. Os canais naturais são formados pela natureza por meio de ações geológicas, geomorfológicas e hidrológicas. Eles incluem todos os cursos de água naturais, do menor ao maior. Um exemplo de um pequeno curso de água é o pequeno riacho ou córrego mostrado na Fig. 2-1. Um exemplo de um grande curso de água é o grande rio mostrado na Fig. 2-2. O maior canal natural é o rio Amazonas em sua foz, mostrado na Fig. 2-3. As aplicações da hidráulica de canal aberto em fluxos naturais são tipicamente nas áreas de controle de inundação, navegação e restauração de fluxo.
|
|
|
Os canais artificiais também podem ser chamados de canais. Eles são normalmente desenvolvidos pelos seres humanos para uma finalidade específica, geralmente para transferir água de um local em que existe um amplo suprimento para um local em que ele é escasso, ou para transferir água entre dois locais para satisfazer diariamente, mensalmente, sazonalmente ou anualmente os requisitos necessários. Canais artificiais também são construídos para controle de inundação e navegação.
Canais artificiais vem sendo construídos desde a época das sociedades antigas, geralmente para transferir água para irrigação ou para fins de abastecimento de água. Exemplificando, a Fig. 2-4 mostra um pequeno canal construído há cerca de 3.500 anos pelos povos antigos de Cajamarca, Peru.
|
Os canais artificiais podem ser nomeados de formas diferentes, dependendo dos seus recursos e finalidades:
-
Canal: Geralmente longo, de inclinação (ou declividade) suave, com ou sem revestimento, apoiado diretamente no solo. O revestimento pode ser composto de vários materiais, como concreto, alvenaria, asfalto ou madeira (Fig. 2-5).

Fig. 2-5 Canal de Irrigação do Distrito de Wellton-Mohawk, Wellton, Arizona.
-
Calha: Canal suportado acima do solo, em escala real ou laboratorial. O revestimento pode ser por meio de vários materiais, como metal, madeira ou acrílico (Fig. 2-6).

Fig. 2-6 Canal de Dulzura no Condado de San Diego, California, EUA,
com sobrecarga após a chuva intensa do dia 05 de março de 2005. -
Calha com declive: Canal com declive muito íngreme (Fig. 2-7).

Fig. 2-7 Canal com declive em Taymi, Lambayeque, Peru.
-
Calha em queda: Canal com queda acentuada a uma distância muito curta, geralmente acompanhando a topografia local (Fig. 2-8).

Fig. 2-8 Canal com queda acentuada usado para fins de irrigação em Arequipa, Peru.
-
Aqueduto: Canal utilizado para transportar água para um uso específico, tipicamente sobre o terreno ou elevado sobre um vale, córrego ou estrada (Fig. 2-9).

Fig. 2-9 Aqueduto de Wari em Sumaq Tika, Cuzco, Peru, datado de 1000 d.C.
-
Galeria: Um conduto livre de comprimento relativamente pequeno, geralmente parcialmente preenchido, para permitir que um riacho atravesse sob uma estrada ou aterro (Fig. 2-10).

Fig. 2-10 Galeria sob a divisa dos EUA e México, no Cânion de Yogurt, na California, EUA.
Usos de canais
Tanto os canais naturais como os artificiais são usados em várias áreas do seguimento de recursos hídricos, incluindo:
Irrigação e drenagem, Fig. 2-11 (a);
Controle de inundação;
Drenagem urbana;
Geração hidrelétrica;
Navegação fluvial;
Abastecimento urbano de água;
Escoamento de águas residuárias;
Recuperação de rios, Fig. 2-11 (b).
A Figura 2-11 (a) mostra um canal de irrigação (à esquerda) e um canal de drenagem (à direita), fluindo em direções opostas, no projeto de irrigação de Wellton-Mohawk, em Wellton, Arizona. A água do canal de irrigação está sendo bombeada à montante, enquanto a água de drenagem está fluindo à jusante.
|
A Figura 2-11 (b) mostra um canal para a passagem de peixes em Ferris Creek, Condado de Plumas, Califórnia.
|
Campos relacionados
Outros campos relacionados que se beneficiam diretamente do conhecimento de hidráulica de canal aberto incluem:
Hidrologia: O estudo da água no ciclo hidrológico.
Geomorfologia fluvial: O estudo da gênese e forma de córregos e rios.
Mecânica dos rios: O estudo das propriedades mecânicas e do comportamento ou rios.
Sedimentologia fluvial: O estudo de sedimentos fluviais, incluindo sua fonte, transporte e destino.
Hidroclimatologia: O estudo do clima e do ciclo hidrológico.
Ecohidrologia: O estudo da interação entre água e vegetação no ciclo hidrológico.
Potamologia: O estudo científico de rios.
2.2 GEOMETRIA DO CANAL
|
|
Os canais naturais se referem ao grande número de córregos e rios ao redor do mundo. No que diz respeito à orientação longitudinal, os canais naturais são classificados como:
retilíneos;
meandrantes;
anastomosados.
Um canal retilíneo é aquele que tende a seguir um caminho reto. Por outro lado, um canal meandrante possui curvas sinuosas, como mostra a Fig. 2-12. A razão entre o comprimento do fluxo e o comprimento do vale é denominada sinuosidade. A sinuosidade do fluxo mostrado é de cerca de 5.
|
Um canal anastomosado apresenta vários subcanais sinuosos interconectados (Fig. 2-13). As condições de fluxo e de sedimentos que levam um canal a assumir uma determinada forma longitudinal são objetos de estudo da geomorfologia fluvial.
|
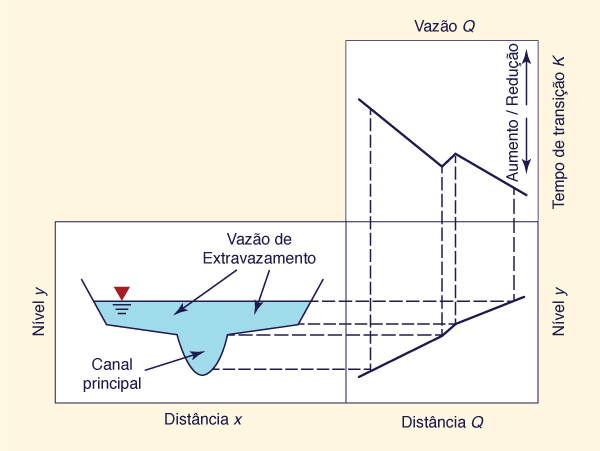
Durante as inundações, os canais naturais podem transbordar e tomar temporariamente porções significativas da planície adjacente (Fig. 2-14). Com relação ao período de inundação, o fluxo nos canais naturais pode estar dentro da calha fluvial, ou seja, quando o fluxo permanece no canal principal, ou fora da calha principal, quando o fluxo transborda para as planícies adjacentes.
|
A Figura 2-15 mostra a variação típica do tempo de viagem K do perímetro de inundação e das suas respectivas ondas de inundação ao logo da sua extensão. Essas variações são devidas aos aumentos ou diminuições de atrito no leito fluvial o estágio de inundação aumenta.
|
Os canais artificiais são classificados como:
prismático;
não prismático.
Os canais prismáticos têm uma seção transversal constante, sendo elas dos tipos trapezoidal, retangular ou triangular. Canais trapezoidais são o tipo mais comum (Fig. 2-16). Canais retangulares são frequentemente usados para o escoamento de obras de saneamento ou experimentos laboratoriais.
|
Os canais não prismáticos são aqueles para os quais a seção transversal não é constante. Canais não prismáticos são usados para a transição de uma seção transversal de um tamanho para outra de tamanho diferente, geralmente em decorrência da variação da declividade do leito.
Canal hidraulicamente amplo
Existem três formas transversais assintóticas em canais prismáticos (Capítulo 1, Seção 1.3):
Hidraulicamente amplo, para o qual o perímetro molhado é constante;
Triangular, para o qual a largura do topo é proporcional à profundidade do fluxo (Fig. 1-9);
Inerentemente estável, para o qual o raio hidráulico é uma constante (Fig. 1-10).
Quando um canal é hidraulicamente amplo (largo), o perímetro molhado P pode ser aproximado pela largura do topo T. Por definição, o raio hidráulico R é igual à área de fluxo A dividida pelo perímetro molhado P. Da mesma forma, a profundidade hidráulica D é igual à área de fluxo A dividida pelo largura do topo T. Portanto, as seguintes relações são válidas para um canal hidraulicamente amplo:
|
P ≅ T | (2-1) |
|
R ≅ D
| (2-2) |
Na prática, um canal pode ser considerado hidraulicamente largo se a largura do topo T for maior ou igual a 10 vezes a profundidade hidráulica D (Chow, 1959):
T _____ ≥ 10 D
| (2-3) |
Em geral:
|
Q = V A | (2-4) |
Em que: Q = vazão;
A = área de escoamento;
V = velocidade média.
Por definição:
|
A = D T | (2-5) |
Sendo que:
|
Q = V D T | (2-6) |
E, consequentemente:
|
q = V D | (2-7) |
Em que: q = vazão unitária da largura do canal.
Para simplificar, um canal hidraulicamente amplo pode ser analisado em termos de sua vazão unitária da largura do canal. Para um canal hipotético de largura unitária, o perímetro molhado é uma constante: P = T = 1. Portanto, um canal hidraulicamente amplo é definido alternativamente como aquele para o qual o perímetro molhado é uma constante. Na prática, a maioria dos canais naturais é hidraulicamente ampla (Fig. 2-17).
|
Hidráulica da seção transversal
A classificação da área de escoamento para a vazão de um canal é:
|
Q = α A β | (2-8) |
Os valores assintóticos de β são (Seção 1.3):
β = 5/3 para um canal hidraulicamente amplo com coeficiente de atrito de Manning turbulento;
β = 3/2 para um canal hidraulicamente amplo com coeficiente de atrito de Chezy turbulento;
β = 4/3 para um canal triangular com coeficiente de atrito de Manning turbulento;
β = 5/4 para um canal triangular com coeficiente de atrito de Chezy turbulento;
β = 1 para um canal inerentemente estável.
Para canais trapezoidais, os valores de β estão entre os valores dos canais hidraulicamente amplos e triangulares. Os valores típicos de β para canais trapezoidais situam-se aproximadamente na faixa de
|
Profundidade de fluxo e seção da profundidade de fluxo
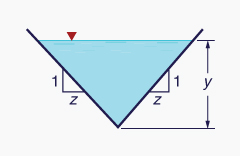
Existem duas profundidades relacionadas ao escoamento de um canal aberto (Fig. 2-19):
A profundidade do fluxo y ;
Seção da profundidade de fluxo d.
A profundidade do fluxo y é a distância vertical medida a partir da superfície livre até o ponto mais baixo da seção transversal do canal. A seção da profundidade de fluxo d é a distância normal à direção do escoamento, medida a partir da superfície livre até o ponto mais baixo da seção transversal do canal.
|
A relação entre a profundidade do fluxo y e a seção da profundidade do fluxo d é:
|
d = y cos θ | (2-9) |
Elementos geométricos
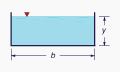
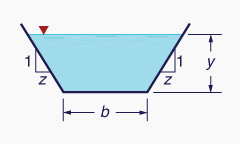
A Tabela 2-1 mostra os elementos geométricos de quatro tipos de seção transversal comumente usadas na engenharia hidráulica.
As propriedades geométricas de uma seção parabólica podem ser
encontradas em
Propriedades geométricas de uma seção parabólica (Mejía e Ponce, 2021).
2.3 DISTRIBUIÇÃO DE VELOCIDADE
|
|
A velocidade média no fluxo de canal aberto é:
Q V = _____ A
| (2-10) |
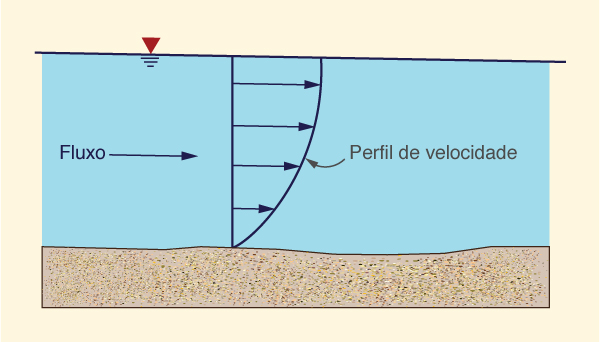
As velocidades locais, no entanto, normalmente variam significativamente. Os perfis de velocidade vertical variam de zero no limite (ou seja, na condição de não escorregamento no fundo do canal) a valores ligeiramente maiores que a média próxima à superfície da água (Fig. 2-20).
|
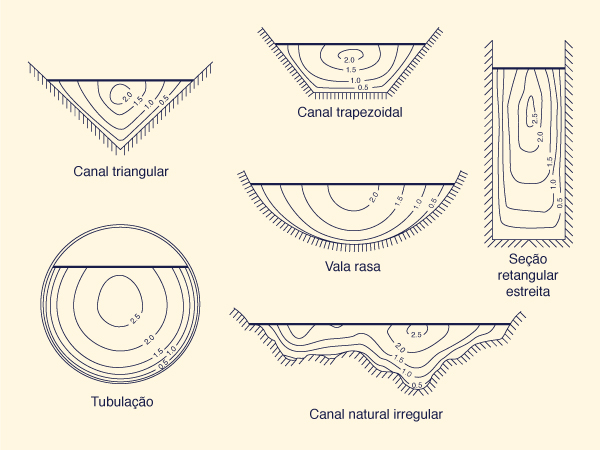
As velocidades transversais também podem variar significamente, de zero (nos limites laterais) a valores máximos (no centro ou perto do meio do canal) (Fig. 2-21). Nos canais mais sinuosos, ou canais de alinhamento curvo, as velocidades são maiores ao longo das laterais externas às margens e menores na parte interna. No entanto, para canais hidraulicamente amplos, os lados têm uma influência desprezível no fluxo. Nesse caso, o fluxo é efetivamente bidimensional (nas direções longitudinal e vertical).
|
A suposição da velocidade média V (Eq. 2-10) reduz ainda mais o fluxo para uma declaração de unidimensionalidade (na direção longitudinal). Essa premissa é estritamente aplicável a canais relativamente retos e para os quais os fluxos permanecem na calha fluvial. De forma a simplificar de modo coerente, a suposição da unidimensionalidade foi aplicada a canais com meandros suaves e escoamentos limitados de extravazamento da calha. No entanto, a suposição da unidimensionalidade geralmente se decompõe para canais de grande sinuosidade e/ou fluxos substanciais de transbordamento da calha (Fig. 2-22).
|
2.4 MEDIÇÕES DE VELOCIDADE
|
|
Medições de velocidade são comumente realizadas usando um medidor de corrente (molinete).
Os medidores em conchas cônicas são amplamente utilizados nos Estados Unidos. O tipo mais comum de medidor de concha é o molinete do tipo Price, que possui seis conchas montadas em um eixo vertical (Fig. 2-23). A velocidade do escoamento é proporcional à velocidade angular do rotor do medidor e é determinada a partir do número de rotações por segundo do rotor, comparando-se com os valores calibrados e tabelados pelo fabricante do medidor.
|
A medição de vazão em uma seção transversal do fluxo requer a determinação da área de escoamento e da velocidade média para um determinado estágio. A seção transversal deve ser perpendicular ao fluxo e a velocidade média deve ser baseada em um número suficiente de medições de velocidade ao longo da seção.
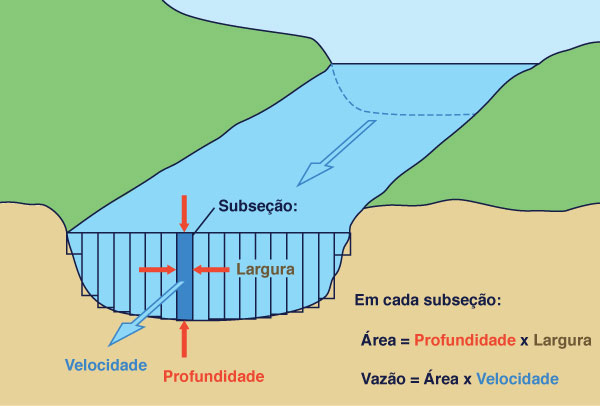
Em um procedimento típico de medição de vazão, cada um dos vários levantamentos de profundidade, geralmente de 20 a 30, define a posição de uma vertical (Fig. 2-24). O valor levantado em cada profundidade é associado a uma seção parcial do escoamento. Uma seção parcial é um retângulo de profundidade igual à sonda e de largura igual à metade da diferença das distâncias para verticais adjacentes. Em cada vertical, são feitas as seguintes observações:
Profundidade do fluxo;
Velocidade medida pelo molinete em um ou dois pontos ao longo da vertical.
|
No método de dois pontos, o molinete é posicionado em 0,2 e 0,8 da profundidade do fluxo. No método de um ponto, o molinete é posicionado a 0,6 da profundidade do fluxo, medido a partir da superfície da água. A média das velocidades a 0,2 e 0,8 de profundidade ou a velocidade única a 0,6 de profundidade é tomada como a velocidade média na vertical. Nas situações em que a medição de dois pontos é impraticável (por exemplo, em fluxos muito rasos), o método de um ponto é recomendado.
Para cada seção parcial, a vazão é calculada da seguinte forma:
q = v a | (2-11) |
Em que: q = vazão;
a = área de escoamento;
v = velocidade média;
Q = soma de todas as vazões de cada subseção.
Os molinetes Price dos tipos AA e A são usados para medições de velocidade de dois pontos em rios com profundidades de fluxo acima de 0,75 m e para medições de um ponto em rios com profundidades variando de 0,45 a 0,75 m. O micromolinete é usado para medições de um ponto em rios rasos ou calhas de laboratório com profundidades na faixa de 0,10 m a 0,45 m.
As técnicas para medir a velocidade do fluxo com um molinete variam com o tamanho do rio. Se o rio for raso, o medidor é afixado a uma haste de profundidade graduada. Se o rio for profundo, o medidor é suspenso em um cabo e mantido na água com um peso. Os pesos podem ser de vários tamanhos, de 6,8 kg a 135 kg. As medidas com molinetes suspensos em cabo são feitas a partir de pontes, teleféricos ou barcos (Fig. 2-25). Para pesos maiores, uma bobina pode ser utilizada para auxiliar a puxar os mesmos de modo a auxiliar a equipe durante o levantamento.
|
2.5 COEFICIENTES DE DISTRIBUIÇÃO DE VELOCIDADE
|
|
Devido à distribuição de velocidade não uniforme ao longo da seção transversal, a carga de velocidade real hv é maior do que a carga de velocidade calculada com base na velocidade média V. Geralmente, a carga real da velocidade é:
V 2 hv = α ____ 2g
| (2-12) |
Em que: α = coeficiente de energia ou ao coeficiente Coriolis. Os valores de Coriolis variam, aproximadamente, de 1,03 a 1,36 para canais prismáticos razoavelmente retos. Os valores mais altos correspondem aos canais menores e os valores mais baixos aos canais maiores.
Da mesma forma que no caso da energia, o momento também requer uma correção devido às velocidades não uniformes (Fig. 2-26). A verdadeira expressão para fluxo de momento (força) é:
|
F = β ρ Q V | (2-13) |
Em que: β = coeficiente de momento ou de Boussinesq;
ρ = densidade mássica da água.
Os valores de β variam entre 1,01 e 1,12 para canais prismáticos relativamente retos. Os valores de α e β são ligeiramente maiores que 1, sendo α sempre maior que β. Para canais com seção transversal composta, os valores de α e β podem facilmente chegar a 1,6 e 1,2, respectivamente (Figs. 2-26 e 2-27). Nos canais de alinhamento irregular, α and β podem variar significamente. Em casos extremos, valores de
|
Coeficiente de Coriolis
Assume-se que:
- A = área total da seção transversal;
- V = velocidade média na seção transversal;
- ΔA = área incremental;
- v = velocidade por meio da área incremental.
A velocidade média é definida como:
Σ v ΔA V = ____________ ... [L T -1] Σ ΔA
| (2-14) |
Em geral, a energia é igual à força integrada a uma distância ou à força multiplicada pelo comprimento:
|
E = ∫ F ds = F L ... [F L] | (2-15) |
A energia cinética para a área total A é igual à massa M multiplicada pela aceleração e pela distância:
1 E = ____ M V 2 ... [M L 2 T -2] 2
| (2-16) |
A energia cinética para a área incremental ΔA é:
1 ΔE = ____ m v 2 ... [M L 2 T -2] 2
| (2-17) |
A carga de velocidade através de ΔA é a energia cinética dividida pelo peso p (sendo o p = mg):
v 2 hv = ______ ... [L] 2 g
| (2-18) |
O fluxo volumétrico através de A é:
|
ΔQ = v ΔA ... [L 3 T -1] | (2-19) |
O fluxo de peso através de ΔA é:
|
Δ(WF) = γ v ΔA ... [F T -1] | (2-20) |
Em que: γ = peso unitário da água.
O fluxo de energia cinética incremental por meio de ΔA é igual à energia cinética por peso hv
γ v 3 ΔA Δ(EF) = ___________ ... [F L T -1] 2 g
| (2-21) |
A soma dos fluxos de energia cinética para todas as áreas incrementais é:
γ v 3 ΔA ∑ Δ(EF) = ∑ ___________ ... [F L T -1] 2 g
| (2-22) |
O fluxo de energia cinética por meio da área total A, com base na velocidade média V , é:
γ V 3 A (EF) = α ___________ ... [F L T -1] 2 g
| (2-23) |
Igualando as Eqs. 2-22 e 2-23 e resolvendo o coeficiente da energia de Coriolis:
Σ v 3 ΔA α = _____________ V 3 A
| (2-24) |
Coeficiente de Boussinesq
O fluxo de massa J através da área total A é igual à densidade mássica multiplicada pelo fluxo volumétrico
|
J = ρ V A ... [M T -1] | (2-25) |
O fluxo de massa J através da área total A é igual à densidade mássica multiplicada pelo fluxo volumétrico incremental ΔQ = v ΔA:
|
ΔJ = ρ v ΔA ... [M T -1] | (2-26) |
Em geral, o momento M é igual à força integrada ao longo do respectivo intervalo de tempo ou à massa multiplicada pela velocidade:
|
M = ∫ F dt = m V ... [M L T -1 ] | (2-27) |
O fluxo de momento, ou força F , é igual ao fluxo de massa multiplicado pela velocidade. Dessa forma, o fluxo de momento através da área incremental ΔA é:
|
ΔF = ρ v 2 ΔA ... [F = M L T -2] | (2-28) |
A soma de todos os fluxos de momento ou soma de forças para todas as áreas incrementais é:
|
∑ ΔF = ∑ ρ v 2 ΔA ... [F] | (2-29) |
O fluxo de momento, ou força F, através da área total é:
|
F = β ρ V 2 A ... [F] | (2-30) |
Igualando as Eqs. 2-29 e 2-30 e resolvendo o coeficiente de momento de Boussinesq:
Σ v 2 ΔA β = _____________ V 2 A
| (2-31) |
|
Formulações aproximadas de α e β
Apesar das Eqs. 2-24 e 2-31 serem precisas, elas requerem medição detalhada da distribuição de velocidade na seção transversal de interesse. Alternativamente, quando apenas a velocidade média V e a velocidade máxima Vmax são conhecidas, as seguintes fórmulas podem ser usadas para calcular os valores aproximados dos coeficientes de Coriolis e Boussinesq (Chow, 1959), conforme o que segue:
Vmax ε = ________ - 1 V
| (2-32) |
Assumindo uma distribuição de velocidade logarítmica, os coeficientes podem ser aproximados como:
|
α = 1 + 3ε 2 - 2ε 3 | (2-33) |
|
β = 1 + ε 2 | (2-34) |
Por outro lado, assumindo uma distribuição de velocidade linear:
|
α = 1 + ε 2 | (2-35) |
ε 2 β = 1 + _____ 3
| (2-36) |
2.6 DISTRIBUIÇÃO DE PRESSÃO
|
|
A distribuição de pressão ao longo da profundidade do fluxo em um canal aberto varia com a forma do fundo do canal em relação à forma da superfície da água, medida ao longo da direção do fluxo. Existem três casos possíveis:
fluxo paralelo;
fluxo curvilíneo convexo;
fluxo curvilíneo côncavo.
Fluxo paralelo
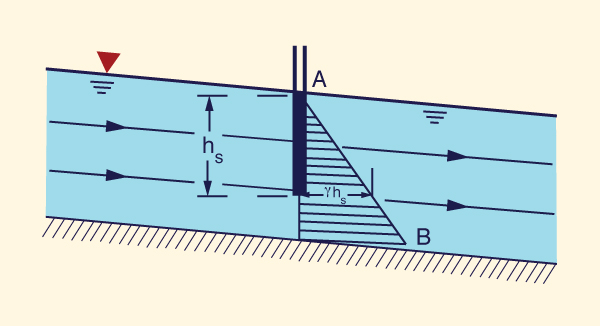
Sob o fluxo paralelo, o fundo do canal é relativamente reto e é paralelo à superfície da água, como no fluxo uniforme (Fig. 2-28), ou aproximadamente paralelo à superfície da água, como no fluxo gradualmente variado. Nesse caso, a distribuição da pressão é essencialmente hidrostática, com a pressão variando linearmente à profundidade do fluxo parcial (linha AB na Fig. 2-28). Na profundidade do fluxo parcial hs, a pressão é: ps = γ hs. Em outras palavras, um piezômetro localizado na profundidade parcial hs abaixo da superfície da água se elevaria para a superfície da água.
|
Na prática, o fluxo uniforme e o fluxo gradualmente variado apresentam uma distribuição de pressão hidrostática (Fig. 2-29). Essa distribuição é caracterizada por velocidades e acelerações nulas ou desprezíveis na direção (quase vertical) normal ao fluxo.
|
Fluxo curvilíneo convexo
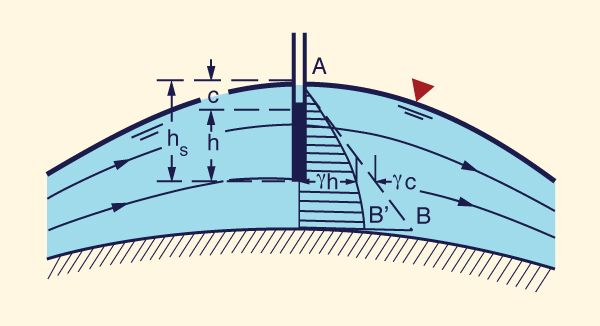
Sob o fluxo curvilíneo convexo, o fundo do canal é substancialmente curvo, apresentando um perfil convexo no plano vertical (Fig. 2-30). Nesse caso, a distribuição da pressão é não hidrostática, com a pressão ao longo da profundidade do fluxo variando como uma função não linear da profundidade do fluxo parcial (curva AB' na Fig. 2-30). Um piezômetro localizado na profundidade parcial hs abaixo da superfície da água se elevaria para um nível mais baixo que o da superfície da água. A verdadeira carga piezométrica é:
|
Na prática, o fluxo rapidamente variado, por exemplo, flui sobre a crista de um vertedouro do tipo Ogee. Esse vertedouro possui o formato similar ao do tipo S, e contem dois arcos que se curvam em direções opostas e terminam em paralelo. São também chamados de arcos canopiais, os quais possuem duas curvas convexas no lado inferior e duas côncavas no lado superior, convergindo em um vértice.
O vertedouro do tipo Ogee, apresenta uma distribuição de pressão não hidrostática (Fig. 2-31).
|
Fluxo curvilíneo côncavo
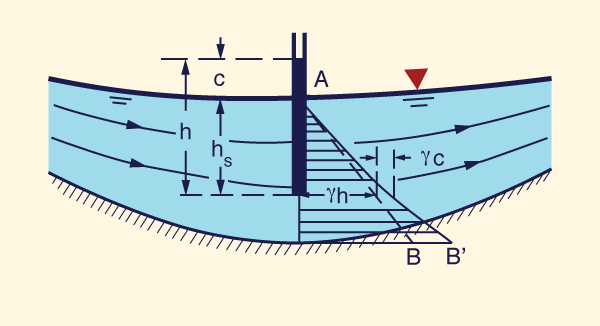
Sob o fluxo curvilíneo côncavo, o fundo do canal é substancialmente curvo, apresentando um perfil côncavo no plano vertical (Fig. 2-32). Nesse caso, a distribuição da pressão é não hidrostática, com a pressão ao longo da profundidade do fluxo variando como uma função não linear em relação à profundidade do fluxo parcial (curva AB' na Fig. 2-32). Um piezômetro localizado na profundidade parcial hs abaixo da superfície da água se elevaria para um nível maior que o da superfície da água. A carga piezométrica real é:
|
Na prática, o fluxo rapidamente variado, ou seja, o escoamento na jusante da soleira de um vertedouro ou em suas proximidades, é caracterizado por uma pressão não hidrostática (Fig. 2-33).
|
A carga de pressão centrífuga c pode ser calculada, aproximadamente, da seguinte forma:
Força centrífuga f = massa multiplicada pela aceleração centrífuga.
Pressão centrífuga pc = massa por unidade de área multiplicada pela aceleração centrífuga.
A carga de pressão centrífuga c = pressão centrífuga dividida pelo peso unitário da água (γ).
A massa por unidade de área é:
|
massa/área = ρ (volume/área) = ρ d = (γ/g) d ... [M L -2 = F T 2 L -3] | (2-37) |
Em que: d = profundidade do escoamento.
A aceleração centrífuga é:
V 2 a = ______ ... [L T -2] r
| (2-38) |
Em que: r = raio de curvatura dos rios.
Assim, a pressão centrífuga pode ser obtida pela multiplicação da Eq. 2-37 pela Eq. 2-38:
γd V 2 pc = _____ _____ ... [F L -2] g r
| (2-39) |
Por fim, a carga de pressão centrífuga pode ser derivada por:
d V 2 c = ____ _____ ... [L] g r
| (2-40) |
Em relação à elevação, ela é considerada negativa para o fluxo curvilíneo convexo e positiva para o fluxo curvilíneo côncavo (Fig. 2-34).
|
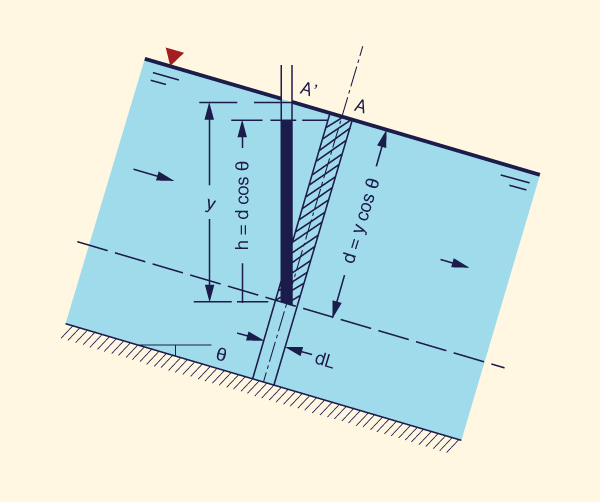
Efeito da declividade na distribuição da pressão
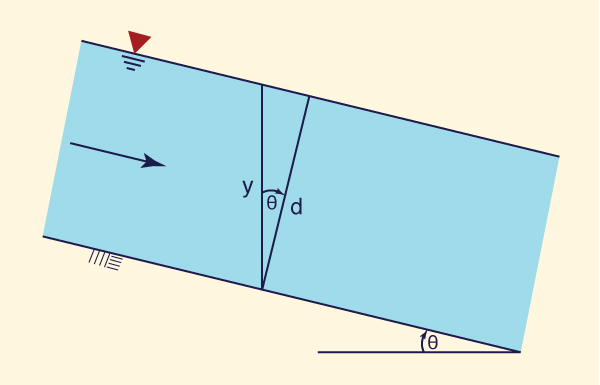
A Figura 2-35 mostra um esquema da distribuição de pressão em um canal com declividade θ. Observa-se o seguinte:
O peso do elemento sombreado é:
γ d dL = γ y cosθ dL ... [F]
| (2-41) |
A pressão exercida pelo elemento sombreado é:
|
γ h = γ d cosθ = γ y cos2θ ... [F L-2] | (2-42) |
O aumento da pressão é:
h = d cos θ = y cos2θ ... [L] | (2-43) |
Para um canal de pequena declividade, h ≅ y, a profundidade vertical y pode ser usada para estimar o aumento da pressão h. No entanto, para um canal de grande declividade, a diferença pode ser substancial.
Uma declividade de 10% (ou seja, uma inclinação igual a 0,1) corresponde a um ângulo θ = 5.7°, para o qual cos2 (5.7°) = 0.99. Assim, para uma declividade superior a 10%, o erro em obter a profundidade vertical y ao invés do aumento da pressão h é superior a 1%. Um canal com inclinação superior a 10% é considerado um canal de grande inclinação.
|
Na prática, um canal de grande declividade apresenta altas velocidades, o que pode levar à entrada de ar, aumento de volume e, consequentemente, ao aumento de profundidade e diminuição de densidade. Assim, a pressão calculada pela Eq. 2-41 pode apresentar um valor ligeiramente superior ao valor real.
QUESTÕES
|
|
O que é uma rampa?
O que é um aqueduto?
O que é uma galeria (ou bueiro)?
O que é potamologia?
O que é sinuosidade em conexão com rios?
O que é um canal hidraulicamente amplo?
Que relação entre a largura do topo e a profundidade hidráulica pode ser considerada hidraulicamente ampla?
Qual é o intervalo típico do expoente β para canais trapezoidais?
Qual é o tipo mais comum de molinete nos Estados Unidos?
Por que a carga de velocidade real é maior que a carga de velocidade calculada com base na velocidade média?
Como a energia se difere do momento?
Como a distribuição de pressão na vertical varia sob o fluxo paralelo?
Como a distribuição de pressão na vertical varia sob o fluxo curvilíneo convexo?
Como a distribuição de pressão na vertical varia sob o fluxo curvilíneo côncavo?
O que é um canal de grande declividade?
PROBLEMAS
|
|
Qual é a vazão por unidade de largura se a vazão for de 24 m3/s e a largura de topo do canal for
T = 8 m? Dado o coeficiente da curva-chave α = 0,4, expoente β = 1,55, área de escoamento A = 45,6 m2, qual é a vazão Q ?
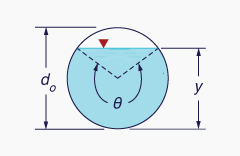
Dado o diâmetro do bueiro do= 1 m, qual é a área de escoamento para θ = 300°? (Veja a Tabela 2-1).
Qual é a força F desenvolvida por uma vazão de Q = 10 ft3/s e velocidade V = 1 ft/s, em uma seção transversal com um coeficiente de Boussinesq β = 1,05?
Um rio com área de escoamento A = 100 m2 é dividido em três seções: (1) margem superior esquerda, com 20% da área de fluxo e velocidade 0,2 m/s; (2) centro da calha, com 70% da área de vazão e velocidade de 1 m/s; e (3) margem superior direita, com 10% da área de vazão e velocidade de 0,1 m/s. Calcule o coeficiente de Coriolis α e o coeficiente de Boussinesq β.
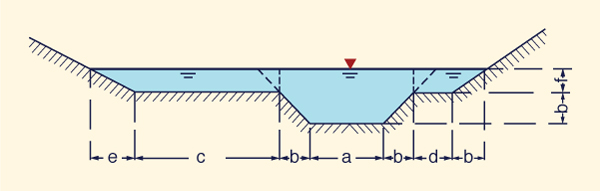
Fig. 2-36 Seção transversal composta.
Verifique os seus cálculos com onlinevelocitycoefficients.php.
Calcule os coeficientes de distribuição de velocidade para os seguintes dados do canal, com a área de fluxo
A = 2768 ft2. Item Velocidade v
(ft/s)Área incremental
do escoamento ΔA (%)1 3.5 0.5 2 4.0 2.9 3 4.5 10.3 4 5.0 23.5 5 5.5 52.7 6 6.0 10.1
Verifique os seus cálculos com onlinevelocitycoefficients.php. Compare os seus resultados com os das fórmulas logarítmicas aproximadas.
Um vertedouro é projetado para uma vazão q = 5 m2/s com uma profundidade de fluxo d = 0,5 m. Qual é o raio mínimo de curvatura da seção transversal do vertedouro necess&aacue;rio para garantir que a pressão não caia abaixo de 50% da hidrostática?
REFERÊNCIAS
|
|
Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, New York.
Ponce, V. M., e D. Windingland. 1985. Kinematic shock: Sensitivity analysis. Journal of Hydraulic Engineering, ASCE, Vol. 111, No. 4, April, 600-611.
| http://ponce.sdsu.edu/canais/index.html |
|
210223 10:15 |