| CAPÍTULO 5: ESCOAMENTO UNIFORME |
5.1 ESCOAMENTO UNIFORME
O fluxo uniforme é estritamente aplicável apenas em canais prismáticos. No fluxo uniforme, a profundidade do fluxo, a área do fluxo, a velocidade média e a vazão são constantes ao longo do canal. Para canais não-prismáticos (naturais) de seção transversal quase uniforme, o termo fluxo de equilíbrio é frequentemente usado para descrever a condição de fluxo que se aproxima ou se assemelha ao fluxo uniforme de canais prismáticos.
Em um escoamento uniforme, todas as declividades (de atrito Sf, de energia Se, da superfície da água Sw e do leito So) são constantes e iguais à declividade S.
Sf = Se = Sw = So = S
| (5-1) |
Não existe escoamento uniforme e instável. Se o fluxo é instável, ele simplesmente não é uniforme.
Estabelecimento de escoamento uniforme
Do ponto de vista mecânico, o fluxo uniforme ocorre em um volume de controle quando a força de atrito é igual à força gravitacional. Na ausência de controles de seção (Seção 4.3), todos os fluxos de canais tendem naturalmente a ter escoamento uniforme.
No fluxo uniforme, a propriedade única da área da curva-chave da vazão ou profundidade qualifica o fluxo uniforme como um controle do canal. Assim, o fluxo crítico uniforme é muito significativo no controle de canais.
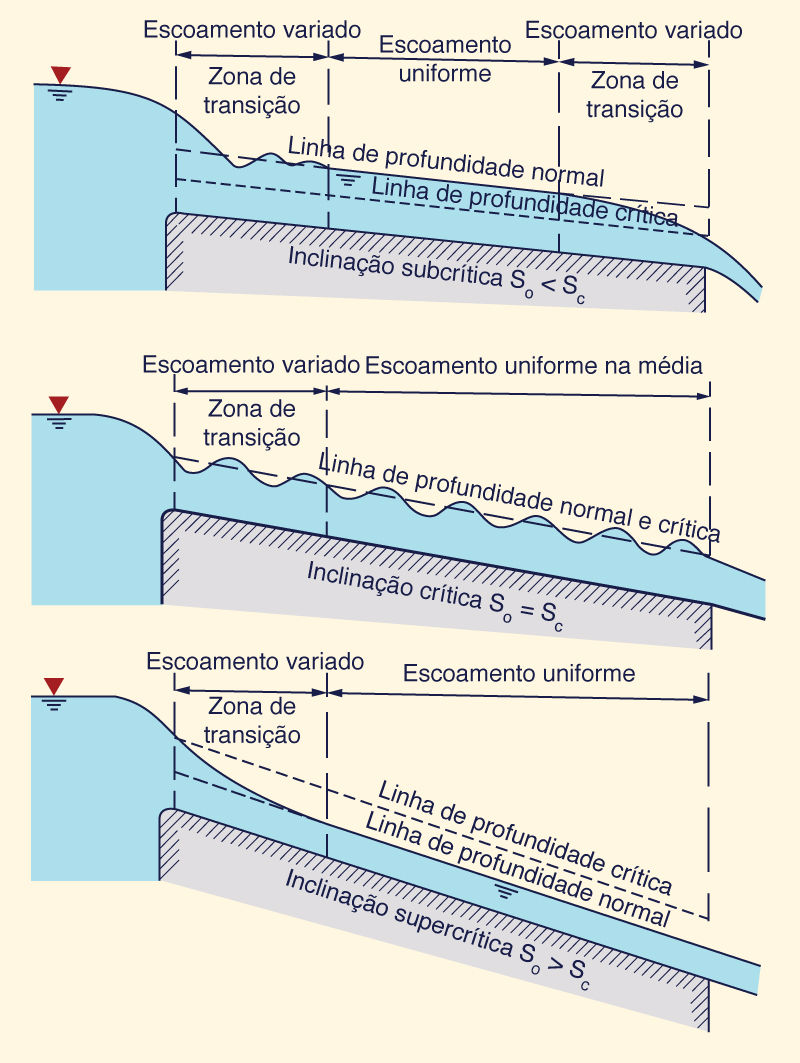
A profundidade do fluxo uniforme é conhecida como profundidade normal. A Figura 5-1 mostra o estabelecimento de fluxo uniforme em um canal suficientemente longo. A figura superior mostra o fluxo normal subcrítico, com controles de seção à montante e à jusante. A figura central mostra o fluxo crítico, com controles de seção à montante e à jusante. A figura inferior mostra o fluxo normal supercrítico, apenas com o controle da seção à montante.
|
Velocidade do fluxo uniforme
Em geral, a velocidade média do fluxo uniforme é descrita pela seguinte fórmula:
V = C R x S y | (5-2) |
Em que: C = coeficiente de atrito;
R = raio hidráulico (sendo R = A/P, onde A = área molhada e P = perímetro molhado);
x e y = expoentes em função da rugosidade e da forma da seção do canal.
Os expoentes x e y variam de acordo com o tipo de rugosidade (laminar, turbulenta, transitória ou laminar-turbulenta mista) e com o formato da seção transversal (arbitrária, hidraulicamente ampla, retangular, trapezoidal, triangular ou inerentemente estável).
Na prática, existem duas fórmulas uniformes de fluxo estabelecidas: (1) a fórmula de Chézy e (2) a fórmula de Manning. Algumas variações dessas fórmulas são atuamente utilizadas, dentre elas a fórmula adimensional de Chézy e a de Manning-Strickler.
5.2 FÓRMULA DE CHÉZY
Para derivar a fórmula de Chézy, a tensão de cisalhamento τb desenvolvida ao longo do fundo do canal é modelada como uma lei de atrito quadrático:
τb = ρ f V 2 | (5-3) |
Em que: ρ = densidade de massa;
f = coeficiente de atrito;
V = velocidade média.
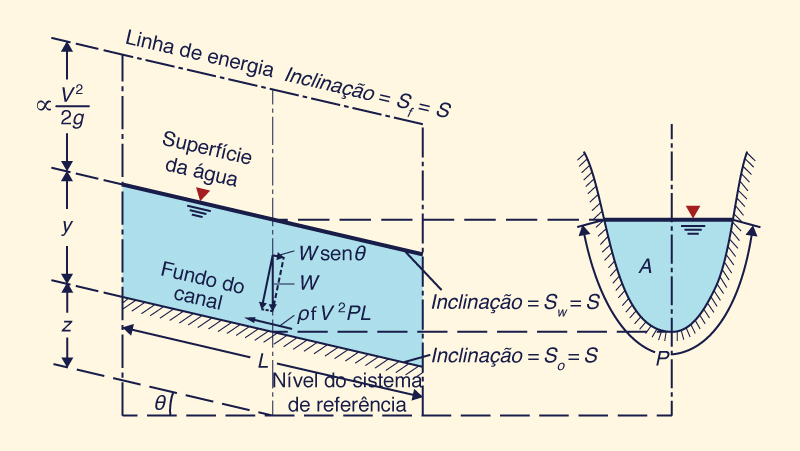
Esta equação é adimensional. Dessa forma, ela tem uma base teórica consolidada. A força de cisalhamento τb desenvolvida ao longo do perímetro molhado P de um volume de controle de comprimento L é (Fig. 5-2):
Fs = τb PL = ρ f V 2 PL | (5-4) |
|
O peso da água no volume de controle é W. Essa força gravitacional está na direção do movimento de forma que:
Fg = W sen θ | (5-5) |
Para um canal de pequena declividade: sein θ ≅ tan θ = S. Portanto:
Fg = W tan θ = W S = γ A L S | (5-6) |
Igualando as forças de atrito (Eq. 5-4) e as gravitacionais (Eq. 5-6):
ρ f V 2 P = γ A S | (5-7) |
Que se reduz a:
f V 2 = g (A /P ) S = g R S | (5-8) |
Em que: R = raio hidráulico.
Resolvendo V:
V = (g/f )1/2 (R S ) 1/2 | (5-9) |
V = C (R S )1/2 | (5-10) |
Em que: C = coeficiente de Chézy.
O coeficiente de Chézy é definido da seguinte forma:
C = (g/f )1/2 | (5-11) |
Assim, o fator de atrito f na Eq. 5-3 é:
g | (5-12) |
A Eq. 5-10 corresponde à fórmula de Chézy. Uma variação da fórmula de Chézy pode ser obtida resolvendo-se a declividade inferior S da Eq. 5-8:
V 2 | (5-13) |
A qual é equivalente a:
D V 2 | (5-14) |
Dada a Eq. 4-6, a Eq. 5-14 é reduzida para:
D | (5-15) |
A Eq. 5-15 é basicamente a mesma da Eq. 4-5, que foi derivada da equação de Darcy-Weisbach aplicada ao fluxo em canal aberto. Assim, a equação adimensinal de Chézy (Eq. 5-15) e a equação modificada de Darcy-Weisbach (Eq. 4-5) são as mesmas.
Para um canal hidraulicamente amplo, D ≅ R,a Eq. 5-15 se reduz à:
|
S = f F 2 | (5-16) |
Que é o mesmo que a Eq. 4-8.
A Tabela 5-1 mostra os valores correspondentes de f, fator de atrito de Darcy-Weisbach f e coeficientes de Chézy.
| [Veja tambén o video do laboratório: Escoamento uniforme]. |
| ||||||||||||||||||||||||||
| ||||
|
Antoine Chézy nasceu em Chalon-sur-Marne, França, em 1 de setembro de 1718 e morreu em 4 de outubro de 1798. Em 1749, trabalhando em Amsterdã, Cornelius Velsen afirmou:
"A velocidade deve ser proporcional à raiz quadrada da inclinação." Em 1757, em Hannover, Alemanha, Albert Brahms escreveu:
Velsen e Brahms estavam trabalhando nas leis e teorias gerais de Torricelli e Bernoulli. Chézy usou algumas dessas idéias para desenvolver sua fórmula.
Foi dada a Chézy a tarefa de determinar a seção transversal e a vazão relacionada para um canal proposto no rio Yvette, que fica perto de Paris, mas em uma altitude mais alta.
Em 1776, Chézy escreveu outro artigo, intitulado: "Fórmula para encontrar a velocidade uniforme que a água terá em uma vala ou em um canal do qual a inclinação é conhecida". V = 272 (ah/p)1/2 Em que: h é a declividade, a é a área e p é o perímetro molhado. O coeficiente 272 é dado para o canal de Courpalet em um antigo sistema de unidades. No sistema métrico, o valor equivalente é: V = 31 (ah/p)1/2 Para o rio Sena, o valor do coeficiente é 44. Clemens traduziu para o inglês os dois artigos de Chézy. Riche de Prony, um dos ex-alunos de Chézy, foi o primeiro a usar a fórmula de Chézy. Mais tarde, em 1801, na Alemanha, Eytelwein usou as idéias de Chézy e De Prony para promover o desenvolvimento da fórmula. |
5.3 FÓRMULA DE MANNING
A fórmula de Manning, em unidades SI, é:
| 1 V = ____ R 2/3 S 1/2 n | (5-17) |
Em que: n = coeficiente de atrito de Manning, fator de atrito ou simplesmente n de Manning.
Nas unidades habituais dos EUA, a fórmula de Manning é:
1,486 | (5-18) |
A quantidade 1,486 é um fator de conversão resultante da equivalência (3,28 pés/m)1/3 = 1.48582 ≅ 1.486. O fator é necessário para expressar a equação original de Manning (Eq. 5-17) em unidades habituais nos EUA.
Para comparar com a fórmula de Chézy, a equação de Manning é expressa da seguinte forma:
1,486 | (5-19) |
Comparando as Eqs. 5-10 e 5-19, obem-se a relação entre os coeficientes de Manning e Chézy:
1,486 | (5-20) |
A equação 5-20 implica que, enquanto C varia com o raio hidráulico, o valor de n não varia. Isso pode acontecer praticamente em canais prismáticos (artificiais), mas geralmente não ocorre em canais naturais (Barnes, 1967).
Nos canais naturais, o valor de n pode variar com o estágio e a profundidade do fluxo. Isso é atribuído a:
Variações naturais na rugosidade do canal com o aumento do estágio, incluindo o efeito dos fluxos de extravazamento (Fig. 2-15 na Seção 2.2), ou
Alterações morfológicas no atrito total do fundo, composto pelo atrito da pele e da forma, à medida que o fluxo sobe do estágio baixo, passando pelo estágio intermediário, até o estágio alto (Simons e Richardson, 1966).
Fórmulas empíricas para o n de Manning
Diversas correlações entre n de Manning e tamanho de partícula (diâmetro do grão) foram desenvolvidas. Williamson (1951) correlacionou o fator de atrito de Darcy-Weisbach f com a rugosidade relativa para produzir a seguinte relação (Henderson, 1966):
| ks | (5-21) |
Em que: ks = rugosidade do grão, em unidades de comprimento;
R = raio hidráulico.
Como f = 8 (g /C 2), a Eq. 5-21 se reduz para:
8g R | (5-22) |
Nas unidades habituais dos EUA, a Eq. 5-22 pode ser convenientemente reduzido para:
1,486 R1/6 | (5-23) |
Comparando a Eq. 5-23 com a Eq. 5-20, n pode ser expresso em termos de rugosidade dos limites da seguinte forma (ks em pés):
n = 0,0311 ks1/6 | (5-24) |
Uma expressão geral para n de Manning em termos de rugosidade relativa e rugosidade absoluta é (Chow, 1959):
n = [f (R/ks)] ks1/6 | (5-25) |
Isso implica que na Eq. 5-24 a rugosidade relativa é uma constante (0,0311).
Supondo que a rugosidade dos limites possa ser representada pelo tamanho de partícula d84, ou seja, aquele para o qual 84% dos grãos (em peso) são mais finos, a Eq. 5-24 converte para:
| n = 0,0311 d841/6 | (5-26) |
Strickler usou uma constante (0,0342) para a função de rugosidade relativa f(R/ks) e o tamanho médio de partícula d50 como o diâmetro representativo do grão, para produzir:
| n = 0,0342 d501/6 | (5-27) |
Já que d84 > d50, as equações de Strickler e Williamson são consideradas mutuamente consistentes.
A Tabela 5-2 mostra os valores n de Manning calculados com a fórmula Strickler (Eq. 5-27).
| ||||||||||||||
| ||||
|
Robert Manning nasceu na Normandia, França, em 1816, e morreu em 1897. Em 1826, mudou-se para Waterford, na Irlanda, e trabalhou como contador. Em 1846, durante o ano da grande fome, Manning foi recrutado para a Divisão de Drenagem Arterial do Gabinete Irlandês de Obras Públicas. Depois de trabalhar como desenhista por um tempo, foi promovido a engenheiro assistente. Em 1848, tornou-se engenheiro distrital, cargo que ocupou até 1855. Como engenheiro distrital, leu "Traité d'Hydraulique" de d'Aubisson des Voissons, após o qual desenvolveu um grande interesse em hidráulica. De 1855 a 1869, Manning foi contratado pelo Marquês de Downshire, enquanto supervisionava a construção do Dundrum Bay Harbor, na Irlanda, e projetou um sistema de abastecimento de água para Belfast. Após a morte do marquês em 1869, Manning retornou ao Gabinete Irlandês de Obras Públicas como assistente do engenheiro-chefe. Ele se tornou engenheiro-chefe em 1874, cargo que ocupou até sua aposentadoria em 1891. Manning não recebeu nenhuma educação ou treinamento formal em mecânica dos fluidos ou engenharia. Sua formação contábil e pragmatismo influenciaram o seu trabalho e o levaram a reduzir os problemas à sua forma mais simples. Ele comparou e avaliou sete fórmulas mais conhecidas da época: Du Buat (1786), Eyelwein (1814), Weisbach (1845), St. Venant (1851), Neville (1860), Darcy e Bazin (1865) e Ganguillet e Kutter (1869). Em seguida, calculou a velocidade obtida de cada fórmula para uma determinada declividade e para o raio hidráulico variando de 0,25 m a 30 m. Então, para cada condição, ele encontrou o valor médio das sete velocidades e desenvolveu uma fórmula que melhor se ajustou aos dados. A fórmula original de melhor ajuste de Manning foi a seguinte: V = 32 [RS (1 + R1/3)]1/2 A qual, posteriormente, ele simplificou para: V = C Rx S1/2 Em 1885, Manning atribuiu a x o valor de 2/3 e escreveu sua fórmula da seguinte maneira: V = C R2/3 S1/2 Em uma carta a Flamant, Manning afirmou: "O recíproco de C corresponde intimamente ao de n , conforme determinado por Ganguillet e Kutter; ambos C e n são constantes para o mesmo canal". Em 4 de dezembro de 1889, aos 73 anos de idade, Manning propôs a sua fórmula à Instituição de Engenheiros Civis da Irlanda. Essa fórmula viu a luz em 1891, em um artigo escrito por ele intitulado "Sobre o fluxo de água em canais e tubulações abertas", publicado nas Transactions of the Institution of Civil Engineers (Irlanda). Manning não gostou de sua própria equação por dois motivos: primeiro, era difícil naqueles dias determinar a raiz cúbica de um número e depois elevá-la ao quadrado utilizando a potência 2/3. Além disso, a equação estava dimensionalmente incorreta e, para obter a correção dimensional, ele desenvolveu a seguinte equação: V = C (gS)1/2 [R1/2 + (0,22/m1/2 )(R - 0.15 m)] Na qual = m = "altura de uma coluna de mercúrio que equilibra a atmosfera" e C = "número adimensional que variava com a natureza da superfície". No entanto, nos livros didáticos do final do século XIX, a fórmula de Manning foi escrita da seguinte maneira:
V = (1/n) R2/3 S1/2
Por meio do seu "Manual de Hidráulica", King (1918) levou à generalização da fórmula de Manning, na forma como é conhecida hoje, bem como à aceitação de que o coeficiente de Manning C deve ser o inverso do n de Kutter . Nos Estados Unidos, n é referido como coeficiente de atrito de Manning, ou simplesmente n de Manning. Na Europa, o Strickler K é o mesmo que o Cn de Manning , ou seja, o recíproco de n. Quando K é usado no lugar de n, a equação de Manning é chamada de equação de Manning-Strickler ou Strickler. |
5.4 COEFICIENTE DE RUGOSIDADE DE MANNING
Dada a Eq. 5-17 (ou 5-18), uma vez conhecidas três das variáveis, a quarta pode ser calculada. Normalmente, R e S são conhecidos e n é estimado, a partir do qual V pode ser calculado. Este é o método direto, a maneira mais típica de usar a equação de Manning.
Quando maior precisão é necessária, ou então, quando n não pode ser estimado com total certeza, recomenda-se uma medição da velocidade V , juntamente com a medição do raio hidráulico R e da inclinação do canal Sn , para calcular n . Este procedimento é chamado de método inverso ou método de calibração. Na prática, a maioria dos aplicativos usou o método direto.
Estimativa do coeficiente n de Manning
Não existe método ou procedimento exato para estimar o n de Manning . Um conjunto comprovado de recomendações é dado abaixo.
Recomendações para a estimativa do coeficiente n de Manning
|
Chow (1959) apresentou uma coleção pictórica de vinte e quatro (24) canais típicos para os quais o n de Manning foi estabelecido. Os valores documentados por Chow variam de n = 0,012 (um canal revestido com lajes de concreto, com superfície muito lisa) até n = 0,150 (um rio natural em solo argiloso, inclinações laterais irregulares e fundo irregular). Chow (1959) listou valores do coeficiente de Manning tão baixo quanto n = 0,008 (lucite, plástico acrílico) até tão alto quanto n = 0,200 (planícies de inundação de córregos naturais, com salgueiros densos, no verão) (Tabela 5-4). Esses valores são aplicáveis escoamento de canais no regime turbulento.
Barnes (1967) apresentou uma coleção pictórica colorida de cinquenta (50) canais de fluxo típicos nos Estados Unidos, para os quais o n de Manning havia sido calculado por calibração. A coleção Barnes pode ser visualizada online em Características de rugosidade dos canais naturais. O valor mais baixo de n de Manning documentado por Barnes é n = 0,024, para o rio Columbia em Vernita, Washington (Fig. 5-3). O valor mais alto de n de Manning é n = 0,075, para Rock Creek, perto de Darby, Montana (Fig. 5-4).
|
|
Arcement e Schneider (1989) apresentaram uma coleção pictórica colorida de quinze (15) planícies de inundação típicas no sudeste dos Estados Unidos, para as quais o n de Manning foi calculado por calibração. A coleção Arcement e Schneider pode ser visualizada online nos Coeficientes de rugosidade de Manning para canais naturais e planícies de inundação. O valor mais baixo de n de Manning, documentado por Arcement e Schneider, é n = 0,100, correspondendo a Cypress Creek, perto de Downsville, Louisiana (Fig. 5-5). O valor mais alto é n = 0,200, correspondendo a Thompson Creek, perto de Clara, Mississippi (Fig. 5-6).
|
|
Na prática, o valor de n de Manning é altamente variável. Nos canais naturais dos rios, pode variar de um pouco mais baixo que 0,020 para alguns rios muito grandes, com um limite relativamente suave (Fig. 5-7), e mais alto que 0,200 para pequenos riachos em córregos íngremes nas montanhas
|
|
| |||||||||||||||||||||||||||||||||
Cowan (1956) desenvolveu uma metodologia racional para estimar o n de Manning. A equação de Cowan é:
| n = (no + n1 + n2 + n3 + n4 ) m5 | (5-28) |
Em que:
no = valor básico de n para um canal reto, uniforme e declividade suave;
n1 = valor adicional para compensar irregularidades na superfície;
n2 = valor adicional considerando as variações no tamanho e formato da seção transversal;
n3 = valor adicional para a compensação das obstruções;
n4 = valor adicional para para a compensação do efeito da vegetação nas condições de escoamento;
m5 = fator relacionado à sinuosidade do canal (meandros).
A Tabela 5-3 lista os valores apropriados a serem usados na Eq. 5-28.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
A Tabela 5-4 lista os valores de n de Manning para canais de vários tipos, compilados por Chow (1959). Para cada tipo de canal, os valores mínimo, normal e máximo de n são mostrados. Os valores normais são recomendados apenas para canais com boa manutenção. Os valores geralmente recomendados para o projeto são mostrados em negrito.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Clicar -aqui- para obter a Tabela 5-4 completa. |
5.5 DETERMINAÇÃO DO ESCOAMENTO UNIFORME
Da Eq. 5-2, a vazão no fluxo de canal aberto é:
Q = V A = C R x S y A | (5-29) |
A equação 5-29 pode ser expressa da seguinte maneira:
Q = K S y = K S 1/2 | (5-30) |
Em que: K = transporte, definido como:
K = C R x A | (5-31) |
Ou, alternativamente:
Q | (5-32) |
De acordo com Chézy:
K = C A R 1/2 | (5-33) |
Segundo Manning, em unidades do SI:
1 | (5-34) |
Nas unidades habituais dos EUA:
1,486 | (5-35) |
O transporte K contém informações sobre atrito, tamanho e forma da seção transversal e é independente da inclinação do canal.
Canais com rugosidade composta
Um canal que transborda geralmente possui mais de um valor de n de Manning, um para a parte interna do escoamento e dois adicionais, um para a margem esquerda e outro para a direita (Fig. 5-9). Um valor composto de n de Manning pode ser calculado sob a suposição de que as velocidades para as três subseções (interna, margem esquerda e direita) permanecem as mesmas. Embora essa suposição seja conveniente, ela evita a possível não uniformidade de fluxo na seção transversal composta.
Considere um canal de rugosidade variável ao longo do seu perímetro úmido, com N sendo o número de subseções. Os perímetros molhados são: P1, P2, P3, ..., PN. Supondo que todas as velocidades são iguais:
V1 = V2 = V3 = VN = V | (5-36) |
Para qualquer subseção i :
1 | (5-37) |
1 | (5-38) |
A área de fluxo da subseção i é:
Vi 3/2 ni 3/2 Pi | (5-39) |
A área total de fluxo do canal é:
V 3/2 n 3/2 P | (5-40) |
A área total do fluxo é igual à soma das subáreas. Portanto:
| (5-41) |
| N |
Da Eq. 5-36, todas as velocidades são iguais. Assim, a Eq. 5-41 reduz para:
| (5-42) |
| N |
Assim, o valor de n de Manning para um canal de seção transversal composta é:
| ∑ (ni 3/2 Pi ) N n = [ _________________ ] 2/3 P | (5-43) |
|
A seção transversal de um canal pode ser composta por várias subseções distintas, e cada uma delas pode ter uma rugosidade diferente. Por exemplo, um canal aluvial sujeito a inundações sazonais geralmente consiste em um canal principal e dois canais laterais (Fig. 5-9). Os canais laterais são geralmente mais ásperos que o canal principal; portanto, a velocidade média no canal principal é geralmente maior que a dos canais laterais. A equação de Manning pode ser aplicada separadamente a cada subseção e a vazão total é igual à soma das vazãos da subseção. Para o canal como um todo, a velocidade média é igual à vazão total dividida pela área total.
O coeficiente de distribuição de velocidade aplicável a todo o canal é diferente dos coeficientes de distribuição de velocidade aplicáveis a cada subseção. O coeficiente de distribuição de velocidade total pode ser calculado como explicado abaixo.
Suponha um número total de subsecções N e várias subsecções i que variam de 1 a N.
Qi = Vi Ai | (5-44) |
Em que: Qi = vazão através subsecção i;
Vi = velocidade média através subseção i na área de fluxo Ai.
Além disso, da Eq. 5-30:
Qi = Ki S 1/2 | (5-45) |
Em que: Ki = transporte através subseção i (Eq. 5-33 ou 5-34).
Combinando as Eqs. 5-44 e 5-45:
Vi = (Ki / Ai) S 1/2 | (5-46) |
A vazão total é:
N Q = ∑ Q i i = 1
| (5-47) |
Usando a Eq. 5-45 na Eq. 5-47:
N Q = ( Σ Ki ) S 1/2 i = 1
| (5-48) |
Da Eq. 2-4, Q = V A. Portanto:
N V = ( Σ Ki ) ( S 1/2 / A ) i = 1
| (5-49) |
Da Eq. 2-24, o coeficiente de energia é reafirmado da seguinte forma:
|
N Σ Vi 3 Ai i = 1 α = _____________ V 3A
| (5-50) |
Da mesma forma, da Eq. 2-31, o coeficiente de momento é:
N Σ Vi 2 Ai i = 1 β = _____________ V 2A
| (5-51) |
Substituindo as Eqs. 5-46 e 5-49 em 5-50, o coeficiente de energia composto α, aplicável a toda a seção transversal, é obtido:
N A2 [ Σ (αi Ki 3 / Ai 2 ) ] i = 1 α = ____________________________ N ( Σ Ki ) 3 i = 1
| (5-52) |
Da mesma forma, substituindo as Eqs. 5-46 e 5-49 em 5-51, o valor composto de β é:
N A [ Σ (βi Ki 2 / Ai ) ] i = 1 β = ____________________________ N ( Σ Ki ) 2 i = 1
| (5-53) |
Exemplo 5-1.
Calcule os coeficientes α e β no pico do fluxo em um canal natural de seção transversal composta (ver Fig. 5-9), com os seguintes dados geométricos e hidráulicos (Adaptado de Chow, 1959):
Solução: Para cada componente i, use a Eq. 5-35 para calcular o transporte K, e
com ele, os componentes das Eqs. 5-52 e 5-53. Um resumo dos resultados é mostrado na tabela a seguir.
Digite as somas de Cols. 3, 8 e 10 desta tabela na Eq. 5-52 para calcular α = 1,42. Da mesma forma, insira as somas de Cols. 3, 8 e 9 na Eq. 5-53 para calcular β = 1,15.
|
Cálculo do fluxo uniforme
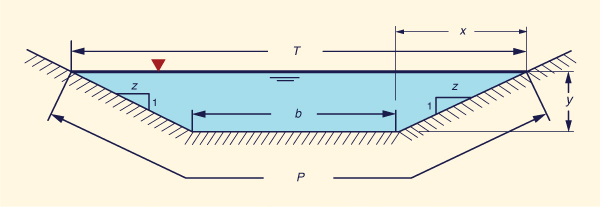
Com referência à Fig. 5-10, a seguinte proporção é válida: z /1 = x /y. Então, a largura do topo T é:
|
T = b + 2x = b + 2zy | (5-54) |
A área de fluxo A é:
A = (b + x ) y = (b + zy ) y | (5-55) |
|
O perímetro molhado P é:
|
P = b + 2 (y 2 + z 2y 2 )1/2 | (5-56) |
Simplificando:
|
P = b + 2 y ( 1 + z 2 )1/2 | (5-57) |
A partir da equação de Manning, a vazão Q é:
| k Q = _____ A R 2/3 S 1/2 n | (5-58) |
Em que: k = 1 em unidades SI e k = 1,486 em unidades habituais nos EUA.
Já que R = A /P, Eq. 5-58 se reduz para:
Q n A 5/3 | (5-59) |
Substituindo as Eqs. 5-55 e 5-57 na Eq. 5-59:
Q n [ (b + zy ) y ] 5/3 | (5-60) |
Simplificando:
| Q n Q n [ (b + zy ) y ] 5/2 - ( ________ ) 3/2 [ 2 y ( 1 + z 2 )1/2 ] - ( ________ ) 3/2 b = 0 k S 1/2 k S 1/2 | (5-61) |
Os dados de entrada que consistem em: (1) vazão Q , (2) largura inferior b, (3) inclinação de tamanho z [z:H to 1:V, Fig. 5-10], (4) inclinação inferior S, e (5) n de Manning. Com dados de entrada fornecidos, Eq. 5-61 é resolvido para a profundidade normal y. Então, com Eqs. 5-54 e 5-55:
A | (5-62) |
Q | (5-63) |
A equação 5-61 é a fórmula geral para fluxo uniforme ou normal, aplicável a canais prismáticos de seção transversal trapezoidal. Para um canal retangular: z = 0. Da mesma forma, para um canal triangular de seção simétrica: b = 0.
Para resolver a Eq. 5-61, é expresso da seguinte forma:
Q n Q n | (5-64) |
Fazendo a alteração da variável x = y para simplificar:
| Q n Q n f (x) = [ (b + zx ) x ] 5/2 - ( ________ ) 3/2 [ 2 x ( 1 + z 2 )1/2 ] - ( ________ ) 3/2 b k S 1/2 k S 1/2 | (5-65) |
A solução da Eq. 5-65 é realizada por um procedimento de tentativa e erro. Um algoritmo iterativo baseado no valor da função é descrito abaixo. Um exemplo de fluxo normal é mostrado na Fig. 5-11.
Algoritmo de profundidade normal com base no valor da função
|
|
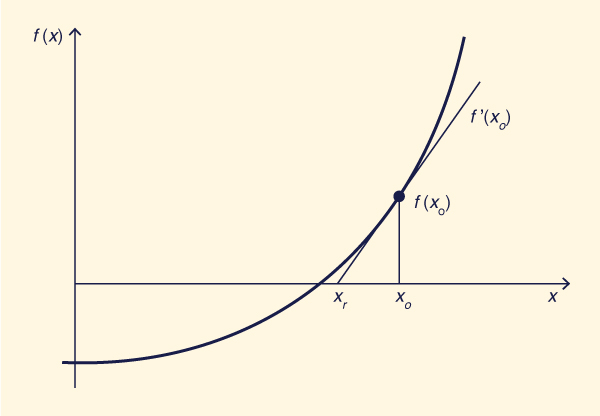
Aproximação de Newton à raiz
A interação acima usa apenas o valor da função para se aproximar da raiz. Um algoritmo mais rápido utiliza a aproximação de Newton, que é baseada na tangente. Observe que, para que a iteração de Newton funcione bem, é necessário primeiro se aproximar da raiz usando a iteração de função descrita acima. Caso contrário, o método tangente de Newton pode não convergir.
Com referência à Fig. 5-12, o valor da tangente em xo é:
f(xo) | (5-66) |
Em que: xo = valor de teste atual de x ;
f(xo) = valor da função em xo ;
xr = novo valor de x, que se aproxima da raiz.
|
Da Eq. 5-66, resolvendo para xr :
f (xo) | (5-67) |
Como mostrado na Fig. 5-12, quando f (xo) aumenta com xo (como é o caso da Eq. 5-65), à medida que a raiz é passada, o valor da função e o valor da tangente são positivos; portanto, o denominador da Eq. 5-66 também é positivo, e xr fica à esquerda de xo. A cada iteração subsequente, a raiz é aproximada para valores ligeiramente superiores ou inferiores, até que a tolerância especificada seja satisfeita.
É facilmente demonstrado que a Eq. 5-67 também se aplica quando f (xo) diminui à medida que xo aumenta, ou seja, como no caso de fluxo crítico, consulte a Seção 4.2.
O valor de f '(x) é:
Q n |
| (5-68) |
Simplificando a Eq. 5-68:
Q n | (5-69) |
O procedimento para a aproximação de Newton da raiz da Eq. 5-65 é descrito abaixo.
Algoritmo de profundidade normal: aproximação de Newton
|
Exemplo 5-2.
Usando a calculadora CANAL EM LINHA 01,
calcule a profundidade normal para as seguintes condições de fluxo: Q = 3 m3/s;
CÁLCULO ONLINE.
Usando a calculadora
CANAL EM LINHA 01, a profundidade normal é |
Exemplo 5-3.
Usando CANAL EM LINHA 01,
calcule a profundidade normal para as seguintes condições de fluxo: Q = 20 ft3/s;
CÁLCULO ONLINE. Usando CANAL EM LINHA 01, a profundidade normal é
|
5.6 DETERMINAÇÃO DA VAZÃO DE CHEIA
Os altos estágios e as rápidas correntes que prevalecem durante as inundações se combinam para aumentar o risco de acidentes e danos à população (Fig. 5-13). Portanto, geralmente não é possível medir a vazão durante a passagem de uma inundação. Uma estimativa do pico de vazão pode ser obtida indiretamente pelo uso de fórmulas de fluxo de canal aberto. Essa é a base do método da área da inclinação .
|
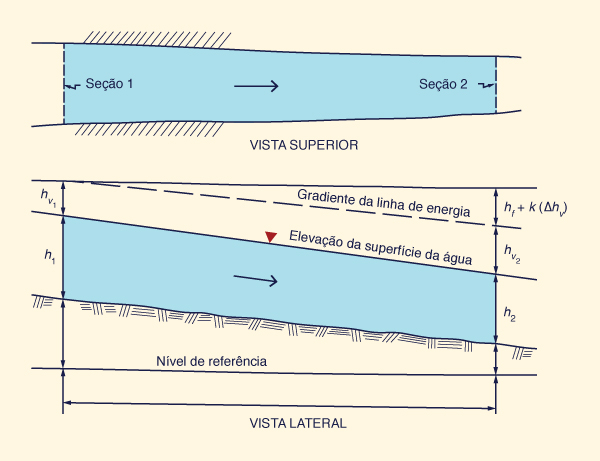
Para aplicar o método da área da declividade para um determinado alcance do rio, são necessários os seguintes dados:
O comprimento do trecho;
A queda, ou seja, a mudança média na elevação da superfície da água ao longo do trecho;
A área de fluxo, o perímetro molhado e os coeficientes da carga de velocidade nas seções transversais à montante e à jusante;
O valor médio de n de Manning para o trecho.
As diretrizes a seguir são usadas na seleção de um trecho adequado:
- As marcas d'água mais elevadas devem ser facilmente reconhecíveis (Fig. 5-14).
O trecho deve ser suficientemente longo para que a queda possa ser medida com precisão.
A forma da seção transversal e as dimensões do canal devem ser relativamente constantes.
O trecho deve ser relativamente reto, embora um alcance de contração seja preferível a um alcance em expansão.
Pontes, curvas de canal, cachoeiras e outros recursos que causam não uniformidade de fluxo devem ser evitados.
|
A precisão do método da área da inclinação melhora à medida que o comprimento do trecho aumenta (Fig. 5-15). Um trecho adequado deve atender a um ou mais dos seguintes critérios:
A relação entre o comprimento do alcance e a profundidade hidráulica deve ser superior a 75,
A queda deve ser maior ou igual a 0,15 m: F ≥ 0,15 m, e
A queda deve ser maior que qualquer uma das cargas de velocidade calculadas nas seções transversais àa montante e à jusante.
|
O procedimento consiste nas seguintes etapas:
Calcule o transporte K nas seções à montante e à jusante:
1
K1 = ( __ ) A1 R1 2/3
n
(5-70a) 1
K2 = ( __ ) A2 R2 2/3
n
(5-70b) Em que: K = transporte;
R = raio hidráulico;
n = valor médio de Manning n no trecho.Nas Eq. 5-70a e 5-70b, os índices 1 e 2 denotam as seções à montante e à jusante, respectivamente. Ambas estão em unidades do SI.
Calcule a condução do trecho, igual à média geométrica dos transportes à montante e à jusante:
K = ( K1 K2 )1/2
(5-71) Em que: K = condução do trecho.
Calcule a primeira aproximação à inclinação da energia:
F
S = ___
L
(5-72) Em que: S = primeira aproximação à inclinação da energia;
F = queda;
L = comprimento do trecho.Calcule a primeira aproximação ao pico de vazão:
Qi = K S 1/2
(5-73) Em que: Qi = primeira aproximação para a vazão de pico.
Calcule as cargas de velocidade:
α1 ( Qi /A1 ) 2
hv1 = ______________
2g
(5-74a) α2 ( Qi /A2 ) 2
hv2 = ______________
2g
(5-74b) Em que: hv1 = carga de velocidade à montante;
hv2 = carga de velocidade à jusante;
α1 = coeficiente de carga de velocidade à montante;
α2 = coeficiente de carga de velocidade à jusante;
g = aceleração da gravidade.Calcule um valor atualizado da inclinação da energia:
F + k ( hv1 - hv2 )
Si = ___________________
L
(5-75) Em que: Si = valor atualizado da inclinação da energia;
k = coeficiente de perda.Para a expansão do fluxo, ou seja, quando
A2 > A1, k = 0,5; para o contração do fluxo, ou seja, paraA1 > A2, k = 1.Calcule um valor atualizado do pico de vazão:
Qi = K Si 1/2
(5-76) -
Volte à Etapa 5 e repita as Etapas 5 a 7. O procedimento é encerrado quando a diferença entre dois valores sucessivos de pico de vazão Q obtidos na Etapa 7 é insignificante. Na prática, isso geralmente é realizado com pelo menos duas iterações.
Exemplo 5-4.
Calcule a vazão de inundação pelo método da área de declive, considerando os seguintes dados:
comprimento do trecho L = 1,450 m; queda F = 2,2 m; valor médio do n de Manning no trecho = 0,035; área de fluxo à montante A1 = 432 m2; perímetro molhado à montante P1 = 85 m; coeficiente de carga da velocidade à montante α1 = 1,15; área de fluxo à jusante A2 = 455 m2; perímetro molhado àjusante P2 = 92 m; e coeficiente de carga da velocidade à jusante α2 = 1,12.
Solução: Use a Eq. 5-70 para calcular a conduçãoo da montante e da jusante K1 = 36.486 and
A coluna 5 mostra o pico de vazão calculado após cada passagem pela Eq. 5-73. O pico final de vazão é mostrado para a Linha i = 2, Coluna 5 (segunda e última iteração).
CÁLCULO ONLINE. Usando a calculadora
EM LINHA DECLIVE AREA, a vazão de inundação é: |
5.7 ESCOAMENTO SUPERFICIAL UNIFORME
O escoamento na planície de inundação de uma bacia é conhecido como fluxo superficial. Nesse caso, a profundidade do fluxo é normalmente muito pequena em comparação com a largura. Sob essas condições, o fluxo pode ser laminar ou turbulento, dependendo da rugosidade absoluta e relativa. Se as velocidades e as profundidades do fluxo são suficientemente pequenas, o fluxo pode ser laminar; caso contrário, o fluxo pode ser transitório ou turbulento, dependendo do número de Reynolds (Seção 1.4).
No fluxo superficial, geralmente existe um regime laminar-turbulento misto. Esse tipo de fluxo é caracterizado por mudanças do regime laminar para turbulento sob as condições de fluxo espacialmente variadas normalmente encontradas no fluxo superficial da bacia hidrográfica.
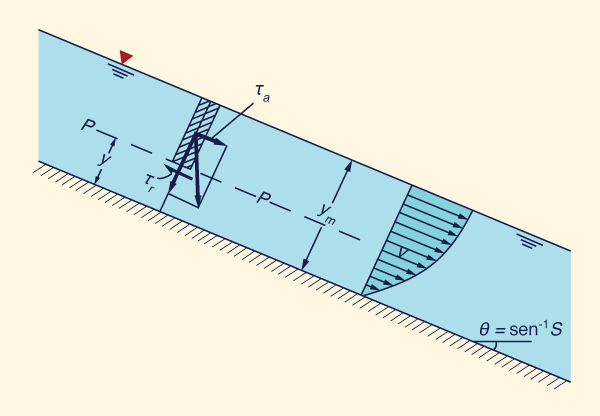
Fluxo de superfície laminar
Com referência à Fig. 5-16, a tensão de cisalhamento de atuação no nível P é:
τa = γ (ym - y ) S | (5-77) |
De acordo com a lei de viscosidade de Newton, a tensão de cisalhamento de resistência em P é proporcional ao gradiente de velocidade vertical:
dv | (5-78) |
Em que: μ = constante de proporcionalidade referida como viscosidade dinâmica.
|
Igualando as tensões de ação e resistência:
dv | (5-79) |
Na forma diferencial:
|
μ dv = γ (ym - y ) S dy | (5-80) |
A densidade de massa γ = ρg e a viscosidade dinâmica μ = ρν, na qual ν = viscosidade cinemática. Assim, a Eq. 5-80 se reduz para:
gS | (5-81) |
Integrando a Eq. 5-81:
gS | (5-82) |
gS y 2 v = _____ [ ym y - _____ ] + C ν 2
| (5-83) |
Em que: C = constante de integração.
Para v = 0, y = 0. Portanto, C = 0, e a relação velocidade-profundidade média do fluxo é:
| gS y 2 v = _____ [ ym y - _____ ] ν 2
| (5-84) |
A Equação 5-84 revela que o perfil de velocidade do fluxo superficial uniforme tem uma distribuição parabólica.
A classificação de profundidade da vazão é obtida pela integração da Eq. 5-84 entre os limites de 0 e ym, ou seja, do fundo para a superfície, para produzir:
| gS y 2 q = ∫ v dy = _____ ∫ [ ym y - _____ ] dy ν 2
| (5-85) |
| gS ym 2 ym 3 q = _____ [ _____ - _____ ] ν 2 6
| (5-86) |
Que se reduz a:
| gS q = ______ ym 3 3ν
| (5-87) |
Ou:
q = CL ym 3 | (5-88) |
Em que: CL = coeficiente da taxa de vazão laminar, que é definido como:
| gS CL = ______ 3ν
| (5-89) |
Observe que, sob fluxo laminar, o expoente da classificação de vazão é β = 3 (Eq. 5-88), e a classificação é uma função do atrito interno, ou viscosidade interna, representada pela viscosidade cinemática ν. Assim, o fluxo laminar é uma função da temperatura.
Dada a Eq. 5-77, a velocidade média no fluxo laminar, v = q /ym, é:
v = CL ym 2 | (5-90) |
A taxa de vazão turbulenta de Chézy é:
q = C S 1/2 ym 3/2
| (5-91) |
A taxa de vazão turbulenta de Manning em unidades do SI é:
q = (1/n) S 1/2 ym 5/3
| (5-92) |
Da mesma forma, em unidades habituais nos EUA é:
q = (1.486 / n) S 1/2 ym 5/3
| (5-93) |
Observa-se que o expoente da classificação varia de β = 3 para fluxo laminar (Eq. 5-88) a β = 3/2 para atrito turbulento de Chézy (Eq. 5-91) ou β = 5/3 para fricção de tripulação turbulenta (Eq. 5-92). No fluxo superficial uniforme, os valores de β na faixa entre laminar e turbulento representam a condição do fluxo laminar-turbulento misto (Seção 1.3).
O número de Vedernikov é:
(β - 1) v | (5-94) |
Sob V = 1, o fluxo é neutro e estável, promovendo o desenvolvimento de ondas de rolagem (Fig. 5-17). A relação entre o expoente β e o número Vedernikov
Relação entre o expoente β e o número de Vedernikov
|
Exemplo 5-5.
Calcular o número de Vedernikov, dado: velocidade de fluxo v = 1 m / s; profundidade do fluxo y = 1 m; e expoente da taxa da área de vazão β = 1,63.
Solução:
Usando a Eq. 5-94: V = (β - 1) v / (gy) = 0,201.
CÁLCULO ONLINE. Usando a calculadora
EM LINHA VEDERNIKOV, o resultado obtido para o número deVedernikov é: |
|
QUESTÕES
Quando o fluxo uniforme se torna instável?
No que a fórmula do Chezy se baseia?
Qual é a diferença entre as fórmulas de Manning e Chezy?
Qual é o valor mínimo do n de Manning que pode ser alcançado na prática?
Qual é o intervalo de valores de n de Manning medido por Barnes?
Qual é o intervalo de valores de n de Manning medido por Arcement e Schneider para planícies de inundação?
Por que o cálculo da rugosidade composta que usa a Eq. 5-43 é considerado apenas uma aproximação?
Quais são as cinco variáveis de entrada usadas no cálculo do fluxo uniforme em um canal trapezoidal?
Por que é melhor usar a aproximação de Newton para a raiz, ao invés de depender apenas da aproximação de funções para resolver o problema de profundidade normal?
Qual é a razão mínima entre o comprimento do trecho e a profundidade hidráulica no método da área de inclinação?
Qual é o expoente da taxa de vazão/profundidade sob condições de fluxo laminar?
Qual é o expoente da taxa de vazão/profundidade sob o atrito turbulento do Chezy em canais hidraulicamente amplos?
Qual é o expoente da taxa de vazão/profundidade sob o atrito turbulento de Manning em canais hidraulicamente amplos?
Sob qual valor do número de Froude é provável que o fluxo se torne instável sob condições de fluxo laminar?
PROBLEMAS
Prove que o fator de atrito de Darcy-Weisbach está relacionado ao n de Manning pela seguinte relação:
fD = 8 g n 2 / (k 2 R 1/3)
Em que: fD = fator de atrito de Darcy-Weisbach, g = aceleração da gravidade, R = raio hidráulico, e k = constante específica para o sistema de unidades, igual a 1 em unidades SI e 1,486 em unidades habituais nos EUA. Expresse a relação em unidades habituais do SI e dos EUA.
Calcule a vazão Q usando a equação de Manning, dado que: área de fluxo A = 23,5 ft2; raio hidráulico R = 5,6 ft; inclinação do canal S = 0,0025; Coeficiente de rugosidade de Manning
n = 0,035. Calcule a vazão Q usando a equação de Manning, dado que: área de fluxo A = 45 m2; raio hidráulico R = 6 m; inclinação do canal S = 0,003; Coeficiente de rugosidade de Manning
n = 0,04. Dado f = 0,0025, calcule a vazão Q for uma área de fluxo A = 12,4 m2, raio hidráulico
R = 2,1 m; e inclinação do canal S = 0,0015.Dado f = 0,0035, calcule a vazão Q for uma área de fluxo A = 18 pés2, raio hidráulico
R = 4,5 pés; e inclinação do canal S = 0,0018.Use a caculadora CANAL EM LINHA 01 para calcular a profundidade normal, velocidade e número de Froude para o seguinte caso: Q = 150 m3/s, b = 10 m, z = 2, So = 0,0005, n = 0,025.
Use a caculadora CANAL EM LINHA 01 para calcular a profundidade normal, velocidade e número de Froude para o seguinte caso: Q = 250 cfs (pés cúbicos por segundo), b = 20 pés, z = 1, So = 0,001, n = 0,030.
Use a caculadora CANAL EM LINHA 15, para cacular a vazão do canal prismático com b = 20 pés,
y = 3 pés, z = 2, n = 0,025, S = 0,0016.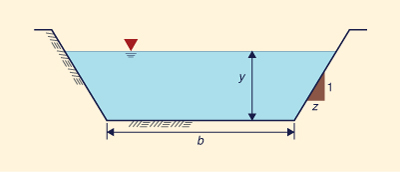
Fig. 5-18 Desenho esquemático do canal trapezoidal.
Use a caculadora CANAL EM LINHA 15, para cacular a vazão do canal prismático com b = 6 m,
y = 1 m, z = 1,5, n = 0,015, S = 0,0002.Uma inundação recente em Clearwater Creek deixou marcas de água observáveis em um determinado trecho do rio. Para estimar a magnitude da inundação, os dados hidráulicos foram medidos em duas seções transversais A e B, a uma distância de 1.850 pés de distância. A queda do trecho entre as seções transversais é de 9,1 pés e o n médio de Manning é de 0,035. A área de fluxo à montante, o perímetro molhado e o coeficiente α de Coriolis são 550 pés2, 55 pés e 1,17; a área de fluxo à jusante, o perímetro molhado e o coeficiente α são 620 pés2, 52 pés e 1,10. Use a calculadora EM LINHA DECLIVE AREA da área de declive para calcular a vazão de inundação.
Calcule a vazão de largura unitária em um plano de fluxo terrestre, sob fluxo laminar, com profundidade média de 1,5 cm e inclinação de 0,001. Assuma a temperatura da água T = 20oC. Relate a vazão em L/s/m.
Usando o cálculo diferencial, encontrar a profundidade relativa y/D em que a vazão é máxima em um bueiro circular de diâmetro D. Explique o motivo desse comportamento.
REFERÊNCIAS
Arcement, G. J. e V. R. Schneider. 1989. Guide for selecting Manning's roughness coefficients for natural channels and flood plains. U.S. Geological Survey Water-Supply Paper 2339, Washington, D.C.
Barnes, H. A. 1967. Roughness characteristics of natural channels. U.S. Geological Survey Water-Supply Paper 1849, Washington, D.C.
Cowan, W. L. 1956. Estimating hydraulic roughness coefficients. Agricultural Engineering, Vol. 37, No. 7, pp. 473-475, July.
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, New York.
Henderson, M. H. 1966. Open-channel flow. Macmillan, New York.
Simons, D. B., e E. V. Richardson. 1966. Resistance to flow in alluvial channels. U.S. Geological Survey Professional Paper 422-J, Washington, D.C.
Williamson, J. 1951. The laws of flow in rough pipes. La Houille Blanche, Vol. 6, No. 5, September-October, p. 738.
| http://ponce.sdsu.edu/canais/index.html |
|
201102 06:35 |