|
|
| CAPÍTULO 1: INTRODUÇÃO |
1.1 ESCOAMENTO EM CANAIS
|
|
O escoamento em condutos livres (ou canais) está em contato com a superfície livre e, por isso, está sujeito à pressão atmosférica (Fig. 1-1). Por outro lado, o escoamento em condutos forçados (ou tubulações) está sujeito apenas à pressão hidráulica que atua no conduto. Devido à sua superfície livre, a análise do fluxo de um canal é geralmente mais complexa que a de um conduto forçado, pois a superfície livre é susceptível a variações espaciais e temporais. Quando o escoamento de um canal não varia no espaço, ele é chamado de uniforme, do contrário ele é variado. Se o escoamento não varia no tempo, ele é chamado de permanente, mas se varia, ele é não permanente.
|
O escoamento dos condutos forçados é delimitado pela seção transversal das paredes do tubo.
Nos condutos forçados, a rugosidade varia de acordo com o material utilizado para a sua confecção, entre outros fatores, desde um latão liso a tubos corroídos, enquanto que nos canais, o rugosidade varia de vidro acrílico ou lucite® (um tipo de plástico muito suave), ambos usados em experimentos laboratoriais, até a dos materiais dos leitos e margens de canais naturais, além das planícies de inundação.
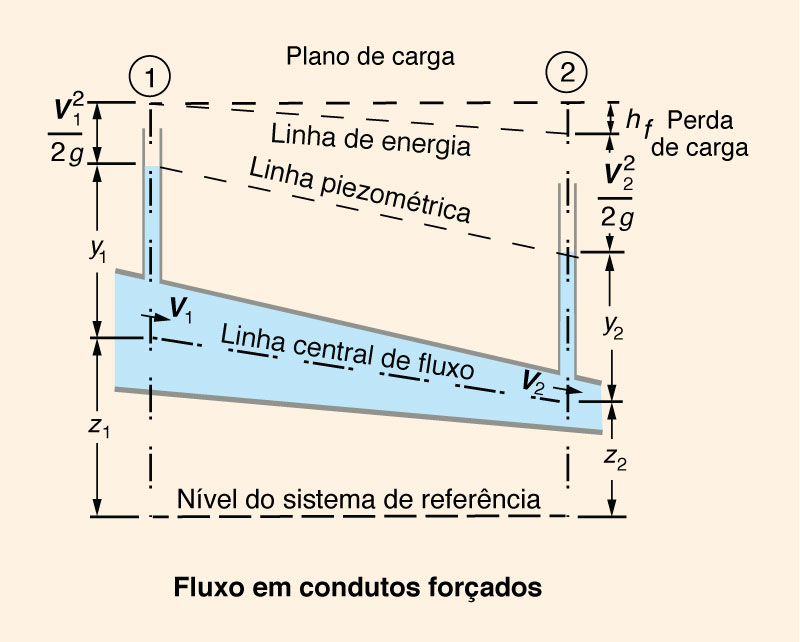
A pressão hidráulica no centro dos condutos forçados define a linha do gradiente hidráulico ou linha piezométrica (Fig. 1-2). A linha de energia corresponde à V 2/(2g) na seção transversal. A perda de carga, ou perda de carga por atrito, da seção 1 à 2, é representada por hf.
|
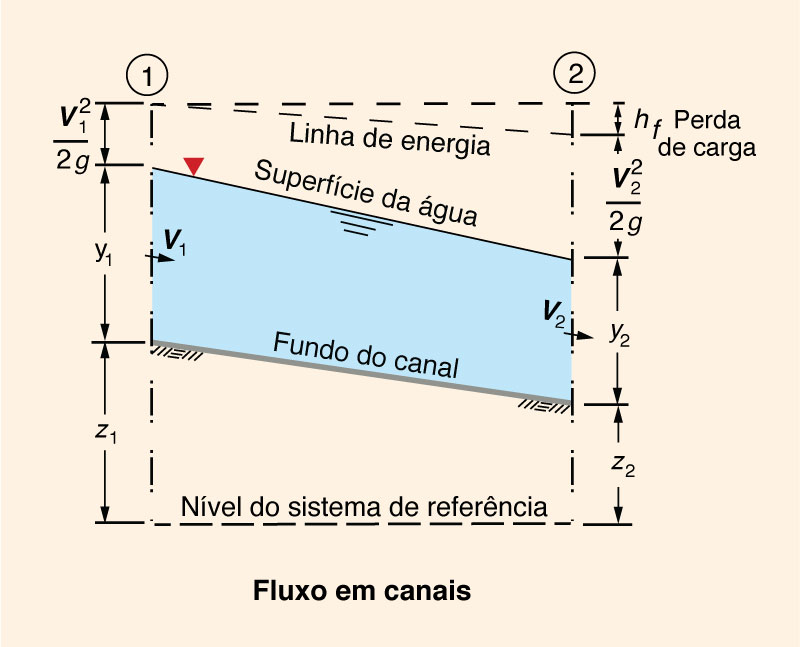
Nos canais, a profundidade do fluxo, medida a partir do leito, define a elevação da superfície da água, equivalente à linha do gradiente hidráulico de um conduto forçado (veja a Figura 1-3). A linha de energia total se refere à parcela de energia cinética V 2/(2g) na seção transversal. A perda de carga, ou perda de carga por atrito, da seção 1 à 2, é representada por hf.
|
Observa-se que no conduto forçado a água sobe até o nível que define a linha do gradiente hidráulico, associada à pressão hidráulica. Por outro lado, no conduto livre, a superfície da água é a linha do gradiente hidráulico que está sujeita à pressão atmosférica.
1.2 TIPOS DE ESCOAMENTO
|
|
Existem dois tipos gerais de seções transversais de canais:
- Prismático;
Não prismático.
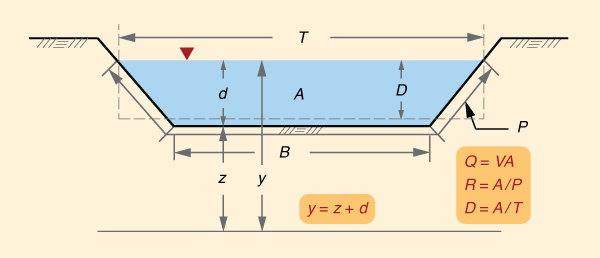
Os canais artificiais (ou feitos pelo homem) são geralmente prismáticos, apresentando uma forma e tamanho constantes, pelo menos para um determinado comprimento de canal. Por outro lado, os canais naturais são tipicamente não prismáticos, isto é, a forma e o tamanho da seção transversal variam ao longo do canal. Várias propriedades geométricas e hidráulicas ajudam a descrever um canal aberto (Fig. 1-4), entre elas:
Vazão Q,
- Área de fluxo A,
Velocidade média V, com V = Q /A,
Perímetro molhado P,
Largura do topo T,
Raio hidráulico R, com R = A /P,
Profundidade hidráulica D, com D = A /T,
Largura do canal B,
Elevação inferior do canal ou elevação do leito z,
Profundidade de fluxo d,
Nível da água na régua limnimétrica em relação ao plano de referência ou elevação da superfície da água, y = z + d.
|
Nos canais prismáticos, a profundidade do fluxo d é conhecida como y, particularmente quando não pode ser confundida com a altura do nível da água obtida pela leitura da régua limnimétrica. Além disso, a inclinação do lado do canal é frequentemente referida como zH:1V, particularmente quando não pode ser confundida com a elevação do leito.
Classificação do escoamento em canais
O fluxo de um canal pode ser classificado da seguinte forma:
Permanente (ou estável) ou não permanente (ou instável);
Uniforme (para canal prismático) ou em equilíbrio (para canal não prismático);
Gradualmente variado ou bruscamente variado;
Espaciamente variado;
O fluxo é permanente quando as variáveis hidráulicas (vazão, área hidráulica, velocidade média, profundidade do fluxo, etentre outras) não variam ao longo do tempo. Do contrário, o fluxo é instável. O escoamento permanente é relativamente simples de calcular, quando comparado com o instável.
O fluxo é uniforme quando o canal é prismático e as variáveis hidráulicas (Q, A, V, d, etc) são constantes no tempo e no espaço. O fluxo está em equilíbrio quando o canal não é prismático e as variáveis hidráulicas são aproximadamente constantes no tempo e no espaço. O cálculo do fluxo uniforme é relativamente direto quando comparado ao de outros tipos de escoamento.
O fluxo varia gradualmente quando a vazão Q é constante, mas as outras variáveis hidráulicas (A, V, d, etc) variam gradualmente no espaço. Sob o fluxo gradualmente variado, a distribuição de pressão na direção vertical, normal ao fluxo, é muito próxima da hidrostática, isto é, proporcional à profundidade do fluxo.
O fluxo varia bruscamente quando a vazão é constante, mas as outras variáveis hidráulicas (A, V, d, etc.) variam bruscamente no espaço, de modo que uma distribuição de pressão hidrostática não possa ser assumida na direção vertical normal ao fluxo. Embora o cálculo do fluxo variado gradualmente seja mais factível, o cálculo do fluxo variado rapidamente é geralmente mais complexo, baseado em fórmulas empíricas, por falta de uma solução teórica.
O fluxo é espacialmente variado quando a descarga Q varia apenas no espaço (ou seja, ao longo do canal), normalmente devido à alguma entrada ou saída lateral.
Ocorrência de vários tipos de escoamento
O escoamento uniforme ocorre em um canal prismático (Fig. 1-5), enquanto que o escoamento em equilíbrio ocorre em um canal não prismático. O fluxo uniforme instável não existe na natureza, porque o fluxo não pode ser uniforme e instável ao mesmo tempo. A palavra "instável" implica em não equilíbrio; portanto, não existe fluxo de equilíbrio instável.
|
O fluxo gradualmente variado e constante é representado pelos perfis da superfície da água, também conhecidos como cálculos de água de retorno (ou rebaixamento) (consulte o Capítulo 7).
O fluxo constante e bruscamente variado é representado pelo fluxo nos vertedouros ou pelo salto hidráulico. O fluxo instável e bruscamente variado é representado pelo salto hidráulico em movimento, surtos, ondas de rolagem, choques cinemáticos e remansos de maré. A Figura 1-6 mostra ondas rolantes em um canal de irrigação íngreme.
O fluxo espacialmente variado ocorre em um canal artificial quando a vazão varia ao longo do canal, devido a extrações laterais da água ou transbordamento do canal.
|
1.3 ESTADO DE ESCOAMENTO
|
|
O estado do fluxo de um canal pode ser descrito em função das velocidades e viscosidades características. Velocidade é a razão do comprimento (distância) ao longo do tempo, com unidades
Razões de velocidade
Existem três velocidades características no fluxo de um canal:
A velocidade média u do escoamento uniforme;
A velocidade ou celeridade ck das ondas cinemáticas;
A velocidade, ou celeridade (na verdade, duas celeridades) cd das ondas dinâmicas.
A velocidade média do fluxo uniforme usando a equação de Manning (unidades SI) é:
1 | (1-1) |
Em que: n = coeficiente de atrito de Manning;
R = raio hidráulico;
S = inclinação de atrito.
A velocidade média do fluxo uniforme constante usando a equação de Chezy é:
|
u = C R 1/2 S 1/2 | (1-2) |
Em que: C = coeficiente de atrito de Chezy.
Em geral, quatro forças estão ativas em um volume de controle no fluxo de canal. Essas forças são causadas por atrito, gravidade, gradiente de pressão (profundidade do fluxo) e inércia. Ondas cinemáticas são aquelas em que o equilíbrio do momento é expresso apenas em termos das forças de atrito e forças gravitacionais (Lighthill and Whitham, 1955).
A celeridade das ondas cinemáticas, ou celeridade de Seddon, é (Seddon, 1900; Chow, 1959; Ponce, 1989):
|
ck = β u | (1-3) |
Em que: β = expoente de classificação da área da curva-chave A, que é definida da seguinte forma:
|
Q = α Aβ | (1-4) |
Em que: α = razão da profundidade hidráulica D com a profundidade do fluxo y.
As ondas dinâmicas são aquelas em que o equilíbrio do momento é expresso apenas em termos do gradiente de pressão e das forças inerciais. A celeridade das ondas dinâmicas é:
|
cd = u ± (g D )1/2 | (1-5) |
Em que: g = aceleração da gravidade;
D = profundidade hidráulica, D = A /T.
Da Eq. 1-3, a celeridade relativa das ondas cinemáticas é:
|
v = (β - 1) u
| (1-6) |
Da Eq. 1-5, o valor absoluto da celeridade relativa das ondas dinâmicas é:
|
w = (g D )1/2 | (1-7) |
Para canais retangulares (onde, D = d ), ou para os canais de grande largura (onde, D ≅ d ), a celeridade relativa das ondas dinâmicas é:
|
w = (g d )1/2 | (1-8) |
A equação 1-8 é conhecida como equação de celeridade de Lagrange (relativa), em homenagem à Lagrange (1788), que a derivou pela primeira vez.
Número de Froude
O número de Froude é definido da seguinte forma (Chow, 1959):
u | (1-9) |
O número Froude caracteriza a condição de:
F < 1: Fluxo subcrítico, ou u < w,
F = 1: Fluxo crítico, ou u = w,
F > 1: Fluxo supercrítico, ou u > w.
Sob o escoamento subcrítico, as ondas de superfície (perturbações) podem fluir para a montante, porque a sua celeridade à montante -w é maior que a velocidade média do fluxo -u.
Sob o escoamento crítico, as ondas superficiais (perturbações) permanecem estacionárias, porque a sua celeridade (absoluta) w é igual à velocidade média do fluxo u.
Sob o escoamento supercrítico, as ondas de superfície (perturbações) podem fluir apenas para a jusante, porque a sua celeridade à montante -w é menor que a velocidade média do fluxo u.
Número de Vedernikov
O número de Vedernikov é definido da seguinte forma (Vedernikov, 1945; 1946; Powell, 1948; Craya, 1952):
v | (1-10) |
O número de Vedernikov caracteriza os seguintes estados de fluxo:
V < 1: Fluxo estável uniforme, ou v < w,
V = 1: Fluxo neutro estável, ou v = w,
V > 1: Fluxo instável, ou v > w.
Sob fluxo estável, a celeridade relativa da onda cinemática v é menor que a celeridade relativa da onda dinâmica w e, portanto, as ondas de superfície (perturbações) são capazes de atenuar (dissipar).
Sob fluxo neutro estável, a celeridade relativa da onda cinemática v é igual à celeridade relativa da onda dinâmica w e, portanto, as ondas superficiais (perturbações) não atenuam nem amplificam.
Sob um fluxo instável, a celeridade relativa da onda cinemática v é maior que a celeridade relativa da onda dinâmica w. Portanto, as ondas de superfície (perturbações) estão sujeitas à amplificação. Na prática, a condição V ~ 1 leva ao desenvolvimento de ondas rolantes, que formam um conjunto de ondas que viajam para rio abaixo, tipicamente em canais artificiais de declive acentuado (Cornish, 1907) (Fig. 1-7).
|
| ||||
|
William Froude nasceu em Dartington, Devon, Inglaterra, em 28 de novembro de 1810 e morreu de acidente vascular cerebral em um cruzeiro para Simonstown, na África do Sul, aos 69 anos. Ele era engenheiro, hidrodinâmico e arquiteto naval.
Em 1832, ele estudou matemática na Universidade de Oxford. Imediatamente após a sua graduação, trabalhou para Isambard Kingdom Burnel, o famoso desenvolvedor de ferrovias, como inspetor da Great Western Railway, na Inglaterra. Em 1857, Brunel o consultou sobre o comportamento do navio Great Eastern no mar. Com base nas recomendações de Froude, Brunel modificou o projeto do navio para evitar a rolar.
A partir de 1859, Froude construiu o primeiro tanque de reboque, usando os seus próprios recursos. Ele realizou experimentos com modelos de navios usando o tanque, primeiramente em sua casa em Paignton, e posteriormente em sua outra casa, em Chelston Cross, em Torquay.
Em 1861, ele escreveu um artigo sobre o projeto da estabilidade de navios em alto mar.
V = k (L)1/2
Em que k é o número que se aplica ao modelo e ao protótipo. Essa lei é conhecida como lei de Froude, embora o próprio Froude tenha reconhecido que Ferdinand Reech (1805-1850) já havia apresentado o conceito vinte anos antes.
O trabalho de Froude foi pioneiro porque ele foi o primeiro a identificar a forma mais eficiente para o casco dos navios, bem como prever a estabilidade do navio tendo como referência modelos de escala reduzida.
Na hidráulica de canais, a Lei de Froude é incorporada ao número de Froude, definido como:
F = V / (gD) 1/2
Em que V = velocidade média, D = profundidade hidráulica, e g = aceleração gravitacional. Diferentemente da relação original de Froude kV, o número de Froude F é adimensional.
|
O expoente β da classificação da área da curva-chave
As três velocidades u, v, e w, levam a apenas duas relações de velocidade independentes, que são os números de Froude (Eq. 1-8) e de Vedernikov (Eq. 1-9). A terceira relação é a celeridade da onda cinemática relativa adimensional, que corresponde ao expoente da classificação da área da curva-chave subtraida de 1:
v
V | (1-11) |
Dessa forma, pode-se verificar que o expoente β na Eq. 1-4 está em função dos números de Froude e de Vedernikov.
O valor de β varia de acordo com o tipo de regime de atrito (laminar, transitório ou turbulento; e Manning ou Chezy turbulento) e com a forma da seção transversal.
Para o escoamento laminar, β = 3. Para o escoamento turbulento, sob atrito de fricção Manning:
Tipos de forma da seção transversal
Existem três formas transversais assintóticas em canais:
Canal hidraulicamente amplo, para o qual o perímetro molhado P é uma constante (Ponce and Porras, 1995). Nesse caso,
β = 5/3 para o coeficiente de atrito de Manning eβ = 3/2 para o coeficiente de atrito de Chezy. Geralmente, uma seção transversal do canal é considerada hidraulicamente ampla para os valores da relação entre a largura superior (do topo) e profundidade do fluxoT /d > 10. Na prática, a maioria dos canais naturais é hidraulicamente ampla (Fig. 1-8).
Nuccitelli Fig. 1-8 Rio Mississipi na ilha Mud, em Memphis, Tennessee.
Canal triangular, no qual a largura do topo T é proporcional à profundidade do fluxo d
(Fig. 1-9). Nesse caso,β = 4/3 para o Coeficiente de atrito de Manning e β = 5/4 para o coeficiente de atrito de Chezy. A drenagem das rodovias (em galerias abertas), geralmente ocorre em seções transversais triangulares.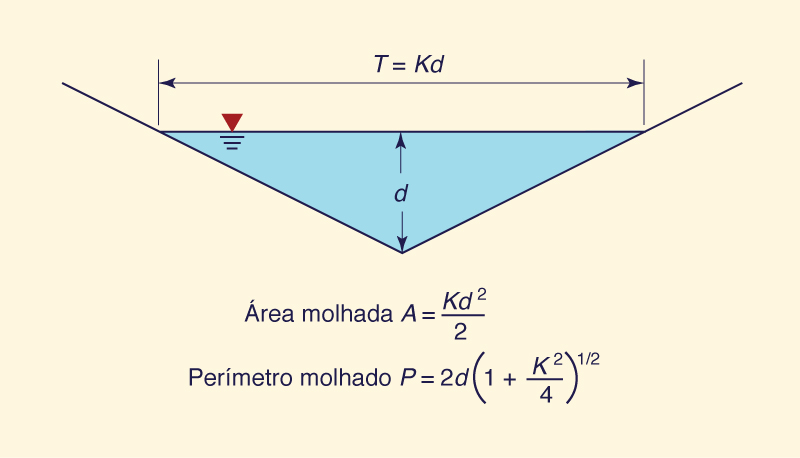
Fig. 1-9 Seção transversal triangular.
Canal inerentemente estável, para o qual o raio hidráulico R é uma constante (Ponce and Porras, 1995). Nesse caso, β ≡ 1 (Fig. 1-10).
Fig. 1-10 Canal inerentemente estável.
Fluxo neutro estável
Para a estabilidade neutra: V = 1. Portanto, da Eq. 1-11, o número de Froude correspondente ao fluxo neutro estável é:
1 | (1-12) |
A Tabela 1-1 mostra os valores de Fns para os valores selecionados de β. Observa-se que, como β varia de 3 (fluxo laminar) para 1 (canal inerentemente estável), o valor de Fns varia de 1/2 a ∞.
Na prática, como o atrito possui efetivamente um limite inferior, o número de Froude é restrito a um limite superior, que raramente excede F = 25. Portanto, na maioria dos casos, um valor de β = 1,04 já seria estável para fins práticos.
| Tabela 1-1 Valores de Fns para os vaores selecionados de β. | |||
| β | Tipo de fricção | Formato da seção transversal | Fns |
| 3 | Laminar | Hidraulicamente amplo | 1/2 |
| 8/3 | Misto laminar-turbulento (Manning 25% turbulento) |
Hidraulicamente amplo | 3/5 |
| 21/8 | Misto laminar-turbulento (Chezy 25% turbulento) |
Hidraulicamente amplo | 8/13 |
| 7/3 | Misto laminar-turbulento (Manning 50% turbulento) |
Hidraulicamente amplo | 3/4 |
| 9/4 | Misto laminar-turbulento (Chezy 50% turbulento) |
Hidraulicamente amplo | 4/5 |
| 2 | Misto laminar-turbulento (Manning 75% turbulento) |
Hidraulicamente amplo | 1 |
| 15/8 | Misto laminar-turbulento (Chezy 75% turbulento) |
Hidraulicamente amplo | 8/7 |
| 5/3 | Manning turbulento | Hidraulicamente amplo | 3/2 |
| 3/2 | Chezy turbulento | Hidraulicamente amplo | 2 |
| 4/3 | Manning turbulento | Triangular | 3 |
| 5/4 | Chezy turbulento | Triangular | 4 |
| 1 | Qualquer | Inerentemente estável | ∞ |
Conforme o mostrado na Tabela 1-1, os valores de β no fluxo de canal e no transbordamento são limitados no intervalo
Relações de viscosidade
Existem três viscosidades características no fluxo de canais:
Viscosidade interna, ou viscosidade cinemática ν do fluido (Apêndice A);
Viscosidade externa (ou difusividade hidráulica νh) do fluxo constante;
Viscosidade externa (ou difusividade das ondas νw) do fluxo instável.
A viscosidade cinemática ν do fluido varia em função da temperatura (Apêndice A). O conceito de difusividade hidráulica νh é devido a Hayami (1951). Hayami combinou as equações de fluxo de canais (Capítulo 10) para desenvolver uma única equação de convecção-difusão, ou seja, uma equação que descreve a convecção (processo de primeira ordem) e a difusão (processo de segunda ordem) de uma onda de inundação. A difusividade hidráulica é definida da seguinte forma:
qo | (1-13) |
Em que: qo = vazão da largura unitária;
So = inclinação (energia) de atrito.
Observa-se que a difusão das ondas de inundação é diretamente proporcional à vazão de largura unitária e inversamente proporcional à inclinação do atrito. A equação 1-13 pode ser expressa em termos de velocidade uo e profundidade do fluxo do da seguinte maneira:
uo do | (1-14) |
Um valor relacionado de difusividade, independente da inclinação, é:
|
νh' = uo do | (1-15) |
Em geral, para uma forma de seção transversal arbitrária:
|
νh' = uo Ro | (1-16) |
Em que: Ro = raio hidráulico
Na teoria das ondas cinemáticas, o comprimento de alcance característico é definido da seguinte forma (Lighthill and Whitham, 1955):
do | (1-17) |
Em que: Lo = comprimento do canal no qual o fluxo de equilíbrio decai no mesmo valor que a sua profundidade. Assim, em termos do comprimento de alcance característico, a difusividade hidráulica é:
uo Lo | (1-18) |
De maneira semelhante à difusividade hidráulica, a difusividade das ondas é convenientemente definida da seguinte forma:
uo L | (1-19) |
Em que: L = comprimento de onda da perturbação.
Número de Reynolds
O número de Reynolds R pode ser expresso da seguinte forma (Chow, 1959):
vh' uo Ro | (1-20) |
O número de Reynolds R descreve o regime de fluxo como:
Laminar;
Transitório;
Turbulento.
Sob condições de fluxo estável no fluxo de canal aberto, o fluxo laminar ocorre para R ≤ 500 e fluxo turbulento para R > 2000. O fluxo de transição ocorre na faixa intermediária: 500 < R ≤ 2000.
Na prática, para a maioria dos casos de escoamento em canais,
o regime é do tipo turbulento.
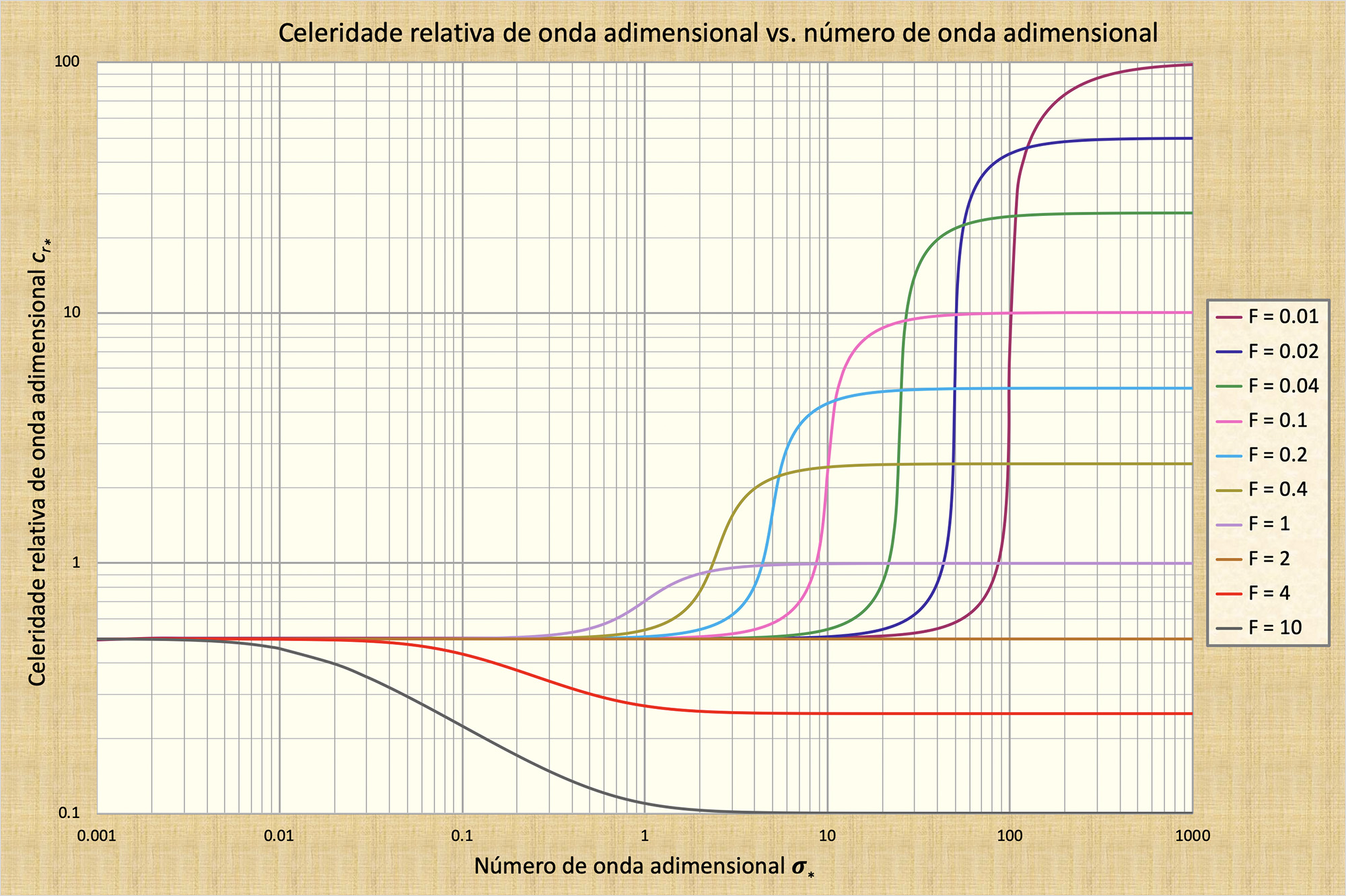
Número de onda adimensional
O número de onda adimensional σ é definido da seguinte forma (Ponce and Simons, 1977):
νh 2 π | (1-21) |
O número de onda σ descreve a escala de comprimento adimensional da onda, como mostrado na Fig. 1-11, em termos de:
ondas cinemáticas;
ondas dinâmicas;
ondas cinemáticas-dinâmicas mistas.
A Figura 11 é aplicável ao caso do coeficiente de atrito de Chezy em canais hidraulicamente amplos.
Sob o escoamento cinemático, descrito no lado esquerdo da Fig. 1-11:
O balanço do momento é descrito apenas em relação às forças de atrito e gravitacionais,
Referente à celeridade da onda cinemática relativa adimensional (Eq. 1-3), uma constante para todos os números de onda e números de Froude prevalece;
A atenuação das ondas é teoricamente zero.
Sob o fluxo dinâmico, descrito no lado direito da Fig. 1-11:
O balanço do momento é descrito apenas em termos do gradiente de pressão e das forças inerciais;
Referente à celeridade dinâmica relativa adimensional (Eq. 1-5), uma constante para todos os números de onda e variações do número de Froude, prevalecem;
A atenuação das ondas é teoricamente zero.
Sob o fluxo misto cinemático-dinâmico, representado na seção central da Fig. 1-11:
O equilíbrio do momento incorpora todas as quatro forças presentes no fluxo instável do canal (de atrito, gravitacional, gradiente de pressão e inercial);
Não há celeridade característica e, portanto, a onda está sujeita a uma atenuação muito forte no intervalo médio dos números de onda adimensionais;
Para cada curva representada na Figura 1-11, a taxa de atenuação é máxima no ponto de inflexão (consulte o Capítulo 10) ( Ponce and Simons, 1977)
|
Difusividade hidráulica dinâmica
A difusividade hidráulica dinâmica, que, diferentemente da difusividade hidráulica de Hayami da
uo Lo | (1-22) |
Para números de Vedernikov baixos, V ⇒ 0, a difusividade hidráulica dinâmica se reduz à expressão de difusividade hidráulica cinemática, isto é, Eq. 1-18. Por outro lado, para números altos de Vedernikov, V ⇒ 1, a difusividade hidráulica dinâmica desaparece. Sob essa condição de fluxo, a ausência total de atenuação das ondas é propícia ao desenvolvimento de ondas rolantes (Figs. 1-6 e 1-7).
|
Na prática de engenharia hidráulica, a onda mista cinemática-dinâmica (que inclui todos os termos da equação do momento de atrito, gravidade, gradiente de pressão e inércia) é comumente referida como "onda dinâmica", seguindo o trabalho de Fread (1993).
No entanto, a onda dinâmica original de Lagrange (1788) representava apenas o gradiente de pressão e a inércia. Para aumentar a confusão, a onda dinâmica de Lagrange tem sido frequentemente chamada de "onda de gravidade". Obviamente, o termo "onda de gravidade" não é apropriado, porque a força da gravidade está ostensivamente ausente de sua formulação.
Assim, parece melhor utilizar o termo "cinemático" para ondas governadas por atrito e gravidade (Lighthill e Whitham, 1955), "dinâmico" para ondas governadas por gradiente de pressão e inércia (Lagrange, 1788), e usar "mista dinâmica-cinemática" para ondas governadas pela abordagem completa do momento (considerando todas as quatro forças). |
1.4 REGIMES DE ESCOAMENTO
|
|
Os regimes de fluxo de um canal podem ser do tipo:
Laminar;
Transitório;
Turbulento.
Os regimes de escoamento são caracterizados pelo número R de Reynolds, Eq. 1-20. No fluxo de um canal, o regime laminar prevalece para R ≤ 500, o regime transitório para 500 < R ≤ 2000 e o regime turbulento para R > 2000.
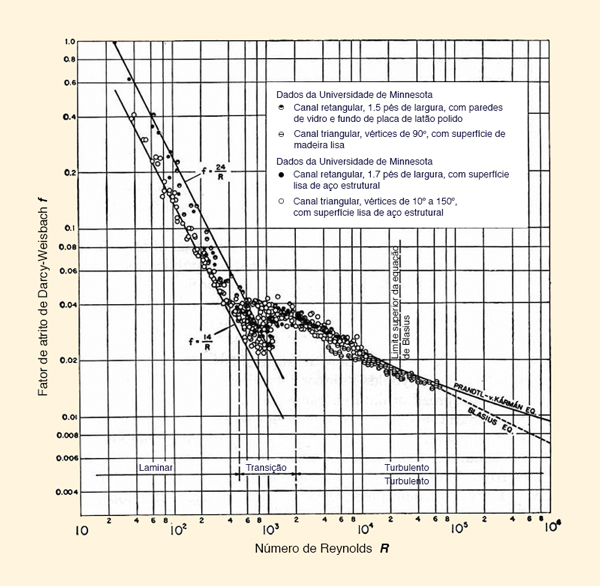
Os regimes de escoamento variam com a rugosidade da superfície do canal. A Figura 1-12 mostra a relação entre o número de Reynolds R e o fator de atrito de Darcy-Weisbach f para o escoamento em canais lisos. A Figura 1-13 mostra a relação entre R e f para o escoamento em canais rugosos.
A fórmula de atrito de Darcy-Weisbach, desenvolvida em paralelo com a do escoamento em tubulações, é:
L
V 2 | (1-23) |
Em que: hf = perda de carga por atrito;
f = fator de atrito de Darcy-Weisbach;
L = comprimento da tubulação;
do = diâmetro da tubulação;
V = velocidade média do fluxo no tubo;
g = aceleração da gravidade;
|
|
Observando-se as Fig. 1-12 e 1-13 pode-se concluir que:
O fluxo laminar prevalece sob baixos números de Reynolds. Sob fluxo laminar, o fator de atrito de Darcy-Weisbach é inversamente proporcional ao número de Reynolds. Em geral:
K
f = _____
R(1-24) Em que: K = constante que varia de acordo com forma e rugosidade do canal.
A constante K varia entre 14 (para canais triangulares) e 24 (para canais retangulares), para superfícies de canal lisas, e entre 33 e 60 para superfícies de canal rugosas.
A faixa de transição não é bem definida, dependendo da forma do canal. Para fins práticos, o intervalo de transição para o escoamento do canal aberto pode ser assumido como:
500 ≤ R ≤ 2.000. Sob um fluxo turbulento, a relação entre f e R segue a fórmula de Blasius (Chow, 1959):
0.223
f = _________
R 0.25(1-25) Esta equação é válida para os números de Reynolds no intervalo: 750 ≤ R ≤ 25.000.
Uma expressão geral para a relação entre f e R foi desenvolvida por von Karman e posteriormente modificada por Prandlt para melhor concordância com os dados aplicáveis. A equação de Prandtl-von Karman resultante é (Chow, 1959):
1
_______ = 2 log (R f 1/2 ) + 0.4
f 1/2(1-26) A equação de Prandtl-von Karman pode ser expressa de forma explícita da seguinte maneira:
1
R = _______ 10 [ ( 1 - 0.4 f 1/2 ) / ( 2 f 1/2 ) ]
f 1/2(1-27)
Fator de atrito de Darcy-Weisbach para o escoamento de canais
A fórmula de Darcy-Weisbach, Eq. 1-23, é estritamente aplicável ao escoamento de condutos forçados. Nessas tubulações, o comprimento de atrito característico é o diâmetro do tubo. Por outro lado, em canais, o comprimento de atrito característico é o raio hidráulico R, isto é, a razão entre a área do escoamento e o perímetro molhado:
A | (1-28) |
Como a área de escoamento de um tubo circular (totalmente cheio) é A = π do2/4, e o perímetro molhado é
L
V 2 | (1-29) |
Em que: V = velocidade média do escoamento no canal.
Em canais com escoamento uniforme, a inclinação da energia, é a mesma do atrito e do leito:
hf
V 2 f V 2 | (1-30) |
Para uma seção transversal de forma arbitrária, o número de Froude é:
V | (1-31) |
Em que: D = profundidade hidráulica: D = A /T.
A equação 1-30 pode ser expressa em relação ao número de Froude, da seguinte maneira:
f D | (1-32) |
A equação 1-32 indica a proporcionalidade entre a inclinação da energia e o número de Froude, com o fator de proporcionalidade, sendo uma função do fator de atrito de Darcy-Weisbach e do fator de forma D /R.
Para um canal hidraulicamente amplo, no qual D ≅ R, a Eq. 1-32 se reduz para:
f | (1-33) |
Assim, para um canal hidraulicamente amplo, o fator de proporcionalidade entre a inclinação da energia e o número de Froude é apenas uma função do fator de atrito de Darcy-Weisbach f. Essencialmente, para o escoamento de canais, deve-se utilizar o fator modificado de Darcy-Weisbach f, igual a 1/8 do fator de atrito convencional f de Darcy-Weisbach. A equação de Darcy-Weisbach modificada para escoamento em canais é:
|
S = f F 2 | (1-34) |
A Tabel 1-2 mostra os valores aproximados do fator de atrito f de Darcy-Weisbach e o correspondente fator de atrito modificado f para valores selecionados de R na faixa turbulenta.
| Tabela 1-2 Valores aproximados para fatores de atrito
f e f para valores selecionados de R na faixa turbulenta. |
||
| R | f | f |
| 2000 | 0,0360 | 0,0045 |
| 4000 | 0,0320 | 0,0040 |
| 7000 | 0,0280 | 0,0035 |
| 10000 | 0,0240 | 0,0030 |
| 15000 | 0,0200 | 0,0025 |
| 60000 | 0,0160 | 0,0020 |
|
A equação 1-33 revela uma propriedade fundamental do escoamento de canais na faixa turbulenta: a proporcionalidade entre a inclinação da energia e o número de Froude.
Para f contante, a inclinação da energia S aumenta proporcionalmente ao aumento do número de Froude e vice versa;
Para F constante, a inclinação da energia S aumenta proporcionalmente ao aumento do fator de atrito f e vice versa.
Para S constante, o número de Froude F aumenta proporcionalmente à diminuição do fator de atrito f e vice versa.
|
QUESTÕES
|
|
Qual é a diferença entre a profundidade do escoamento d e a profundidade hidráulica D ?
É possível um fluxo uniforme instável? Por quê?
Quais são as quatro forças que atuam no equilíbrio do momento do escoamento de um canal?
O que é uma onda cinemática?
O que é uma onda dinâmica de acordo com Lagrange?
Qual é a definição do número de Froude?
Qual é a definição do número de Vedernikov?
O que é o fluxo neutro e estável?
Qual é a faixa normal no expoente β da classificação da área da curva-chave de um canal?
Qual tipo de atrito é descrito por β = 2?
Para qual condição o valor de β pode ser menor que 1?
Qual a definição do número de Reynolds?
Qual é o intervalo geralmente estimado para os valores do número de Reynolds durante o regime de transição do escoamento de um canal?
Qual é o número de onda adimensional?
As ondas cinemáticas atenuam?
As ondas dinâmicas atenuam?
As ondas cinemáticas-dinâmicas mistas atenuam?
Qual é o tipo de onda de escoamento de um canal que mais atenua?
Para qual valor do número de onda adimensional a taxa de atenuação de ondas cinemáticas-dinâmicas mistas é máxima?
Qual é a celeridade relativa da onda cinemática adimensional sob a força de atrito de Chezy para um canal hidraulicamente amplo?
Qual é o comprimento de alcance característico?
Qual é a difusividade hidráulica?
Para qual valor da inclinação do canal a difusividade hidráulica é máxima?
Qual é a difusividade hidráulica dinâmica?
Sob que condição de fluxo a difusividade hidráulica dinâmica desaparece?
Na prática de engenharia hidráulica, a que normalmente se refere o termo "onda dinâmica"?
Qual é a fórmula de Darcy-Weisbach modificada aplicada ao fluxo em canal?
Qual é a faixa típica do fator de atrito de Darcy-Weisbach f na faixa turbulenta?
Qual é a faixa típica do fator de atrito modificado de Darcy-Weisbach f na faixa turbulenta?
Existe um limite superior teórico para o número de Froude? Como pode ser calculado?
PROBLEMAS
|
|
Derive a expressão para o ângulo θ em um canal circular (bueiro) em função da profundidade do escoamento y e do diâmetro D, em que: D = 2r (Fig. 1-14).
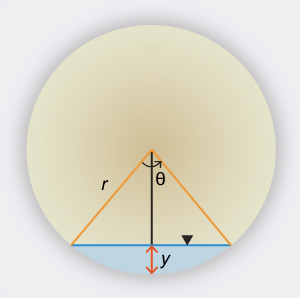
Fig. 1-14 Desenho esquemático de um canal circular.
Mostre que a vazão máxima em um canal circular (Fig. 1-14) é atingida em y = 0.94 D. Use o CANAL EM LINHA 03. Explique a razão desse comportamento.
Derive a fórmula para a área de escoamento A, perímetro molhado P e largura do topo T para um canal trapezoidal, em termos de profundidade do fluxo y, largura inferior b e inclinação lateral z considerando-se a relação zH:1V (Fig. 1-15).
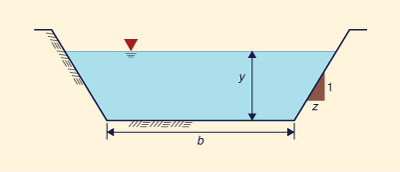
Fig. 1-15 Desenho esquemático de um canal trapezoidal.
Supondo um canal trapezoidal com profundidade do fluxo y, largura do fundo b e inclinação lateral zH:1V (Fig. 1-15). Para um valor dado de z, derive uma expressão para a razão largura/profundidade b/y como função de α, que é a razão da profundidade hidráulica D com a profundidade do fluxo y. Para z = 1 e α = 0,99, qual é o valor de b/y?
Calcule a celeridade relativa da onda cinemática adimensional sob o coeficiente de atrito de Manning para um canal hidraulicamente amplo.
Qual é o valor de β para um canal hidraulicamente amplo no número Froude
F = 1,8 e número de Vedernikov V = 0,9?Um canal hidraulicamente amplo tem profundidade de fluxo = 1 m e velocidade de fluxo = 1,5 m / s. Calcule o número de Froude. Confirme com EM LINHA FROUDE.
Um canal hidraulicamente amplo tem um expoente da classificação β = 1,6. A profundidade do fluxo é de 1 m, e a velocidade do fluxo é de 1,5 m/s. Calcule o número de Vedernikov. Confirme com EM LINHA VEDERNIKOV.
Dado um canal hidraulicamente amplo com coeficiente de atrito de Manning e velocidade média u = 1 m/s, profundidade do fluxo d = 1 m e inclinação inferior S = 0,001. Determine as difusividades hidráulicas cinemáticas e dinâmicas.
Dado um canal hidraulicamente amplo com coeficiente de atrito de Chezy e profundidade de fluxo d = 1 m. Qual velocidade média fará com que a difusividade hidráulica dinâmica desapareça?
De acordo com a equação de Blasius, qual é o número de Reynolds R correspondente ao fator de atrito de Darcy-Weisbach f = 0,03?
De acordo com a equação de Prandt-von Karman, qual é o número de Reynolds R correspondente ao fator de atrito de Darcy-Weisbach f = 0,03?
Sendo a inclinação a jusante do vertedouro WES de 0,6H:1V e fator de atrito de Darcy-Weisbach de f = 0,03, calcule o número máximo possível de Froude para essas condições.
Supondo um número máximo possível de Froude F = 25, calcule o valor de β que garantirá um fluxo neutro e estável.
Um canal prismático escoa próximo ao nível crítico. A inclinação inferior é de S = 0,004. Qual é o valor do coeficiente de atrito modificado de Darcy-Weisbach f?
REFERÊNCIAS
|
|
Chow, V. T. 1959. Open-channel Hydraulics. Mc-Graw Hill, New York.
Cornish, V. 1907. Progressive waves in rivers. The Geographical Journal. Vol. 29, No. 1, January, 23-31.
Craya, A. 1952. The criterion for the possibility of roll wave formation. Gravity Waves, Circular 521, 141-151, National Institute of Standards and Technology, Gaithersburg, Md.
Dooge, J. C. I., W. B. Strupczewski, and J. J. Napiorkoswki. 1982. Hydrodynamic derivation of storage parameters in the Muskingum model. Journal of Hydrology, 54, 371-387.
Fread, D. 1993. "Flow Routing," Chapter 10 in Handbook of Hydrology, D. R. Maidment, editor, McGraw-Hill, New York.
Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, December.
Lagrange, J. L. de. 1788. Mécanique analytique, Paris, part 2, section II, article 2, p 192.
Lighthill, M. J., and G. B. Whitham. 1955. On kinematic waves: I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.
Ponce, V, M., and D. B. Simons. 1977. Shallow wave propagation in open-channel flow. Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, December, 1461-1476.
Ponce, V. M. 1989. Engineering Hydrology: Principles and Practices. Prentice-Hall, Englewood Cliffs, New Jersey.
Ponce, V. M. 1991a. The kinematic wave controversy. Journal of Hydraulic Engineering, ASCE, Vol. 117, No. 4, April, 511-525.
Ponce, V. M. 1991b. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.
Ponce, V. M., and P. J. Porras. 1995. Effect of cross-sectional shape on free-surface instability. Journal of Hydraulic Engineering, ASCE, Vol. 121, No. 4, April, 376-380.
Powell, R. W. 1948. Vedernikov's criterion for ultra-rapid flow. Transactions, American Geophysical Union, Vol. 29, No. 6, 882-886.
Seddon, J. A. 1900. River hydraulics. Transactions, ASCE, Vol. XLIII, 179-243, June.
Vedernikov, V. V. 1945. Conditions at the front of a translation wave disturbing a steady motion of a real fluid, Dokl. Akad. Nauk SSSR, 48(4), 239-242.
Vedernikov, V. V. 1946. Characteristic features of a liquid flow in an open channel, Dokl. Akad. Nauk SSSR, 52(3), 207-210.
| http://ponce.sdsu.edu/canais/index.html |
|
200720 08:00 |