2.1  TIPOS DE CANALES

[Geometría de Canales]   [Distribución de Velocidades]   [Medición de Velocidades]   [Coeficientes de Distribución de Velocidades]   [Distribución de Presiones]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]

Existen dos tipos de canales: (1) naturales, y (2) artificiales. Los canales naturales son formados por la naturaleza a través de acciones geológicas, geomorfológicas, e hidrológicas. Todas las corrientes naturales de agua, desde la más pequeña hasta la más grande se conocen como canales naturales. La Fig. 2-1 muestra un arroyo, ejemplo de un canal con poco flujo de agua. La Fig. 2-2 muestra un ejemplo de canal natural con gran cantidad de flujo de agua. La Fig. 2-3 muestra el canal natural más grande del mundo: el Río Amazonas. Las aplicaciones de la hidráulica de canales en corrientes naturales son típicamente para control de inundaciones, navegación, y la restauración de corrientes naturales.

Fig. 2-1  Un pequeño riachuelo, aguas arriba de la presa Sheep Creek Barrier, Utah.

Nuccitelli Fig. 2-2  El Río Mississippi en Mud Island, Memphis, Tennessee.

Fig. 2-3  El Río Amazonas cerca de su desembocadura, Macapá, Amapá, Brasil.

A los canales artificiales se les conoce simplemente como canales. Éstos son construidos por el hombre para satisfacer necesidades específicas; por ejemplo, para transferir agua de un lugar con abundancia a un lugar de escasez. Además, para transferir agua entre dos localidades para satisfacer necesidades diarias, mensuales, estacionales o anuales. Adicionalmente los canales se construyen para control de inundaciones y navegación.

Históricamente los canales han sido construídos con el fin de transferir agua para riego o abastecimiento. La Fig. 2-4 muestra un pequeño canal construído hace aproximadamente 3,500 años por los antiguos pobladores de Cajamarca, Perú.

Fig. 2-4  El Canal de Cumbemayo, cerca de Cajamarca, Perú.

A los canales se les conoce con diversos nombres, dependiendo de sus características y uso previsto, por ejemplo:

• Canal:  Generalmente largo y de pendiente suave, con o sin revestimiento, apoyado sobre el terreno. El revestimiento puede ser de concreto, mampostería, asfalto, o madera (Fig. 2-5).

  Fig. 2-5  Canal de irrigación, Distrito de riego Wellton-Mohawk, Wellton, Arizona.

• Canal elevado:  Canal apoyado por encima del terreno, ya sea a escala natural o de laboratorio. El revestimiento puede ser de metal, madera o acrílico (Fig. 2-6).

  Fig. 2-6   El conducto de Dulzura, en el Condado de San Diego, California, desbordando después de fuertes lluvias, el 5 de Marzo del 2005.

• Rápida:  Un canal de pendiente muy pronunciada (Fig. 2-7).

  Fig. 2-7  Rápida en el Canal Taymi, Lambayeque, Perú.

• Caída:  Canal de caída rápida y distancia muy corta, generalmente para ajustarse a la topografía (Fig. 2-8.).

  Fig. 2-8  Caída en un canal de irrigación, Arequipa, Perú.

• Acueducto:  Canal para transportar agua para algún uso específico. Por lo general se construyen sobre el terreno, o elevado sobre un valle, arroyo o camino (Fig. 2-9).

  Fig. 2-9  El acueducto Wari en Sumaq Tika, Cuzco, Perú, c. 1,000 A.D.

• Alcantarilla:  Conducto (o conductos) cubierto, de longitud relativamente corta, que permite el paso de un arroyo por debajo de una carretera o terraplén. Por lo general, fluye parcialmente llena (Fig. 2-10).

  Fig. 2-10  La alcantarilla del Cañón Yogurt, California, que cruza la frontera entre Estados Unidos y México.

Usos de los Canales

Los canales se utilizan en diversas áreas de la hidraúlica, como son:

• Irrigación y drenaje,

• Control de inundaciones,

• Drenaje urbano,

• Generación de energía hidroeléctrica,

• Navegación fluvial,

• Suministro de agua potable,

• Drenaje de aguas servidas, y

• Restauración de cauces naturales.

La Figura 2-11 muestra un canal utilizado para el paso de peces, en Ferris Creek, Condado de Plumas, California.

Fig. 2-11  Canal de pasaje de peces en el Arroyo Ferris restaurado, Condado de Plumas, California.

Áreas Relacionadas

Algunas áreas relacionadas a la hidráulica de canales que se benefician directamente de ella son:

• Hidrología:   El estudio del agua en el ciclo hidrológico.

• Geomorfología fluvial:  El estudio de la génesis y la forma de los arroyos y ríos.

• Mecánica fluvial: El estudio del comportamiento y las propiedades mecánicas de los ríos.

• Sedimentología fluvial:   El estudio de los sedimentos fluviales, incluyendo su origen, transporte y destino.

• Hidroclimatología:  El estudio del clima y el ciclo hidrológico.

• Ecohidrología:   El estudio de la interacción entre el agua y la vegetación.

• Potamología:  El estudio científico de los ríos.

2.2  GEOMETRÍA DE CANALES

[Distribución de Velocidades]   [Medición de Velocidades]   [Coeficientes de Distribución de Velocidades]   [Distribución de Presiones]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Tipos de Canales]

El término "canales naturales" se usa para referirse al gran número de arroyos y ríos que existen en la naturaleza. De acuerdo a su orientación longitudinal, los canales naturales se clasifican en: (a) rectos, (b) meándricos, o (c) trenzados.

Un canal recto es aquél que sigue aproximadamente una trayectoria rectilínea. Un canal meándrico es aquél que visto en planta tiene curvas como las que se muestran en la Fig. 2-12. La relación entre la longitud del cauce y la longitud del valle se conoce como índice de sinuosidad, o simplemente sinuosidad. La sinuosidad de la corriente que se muestra en la Fig. 2-12 es de aproximadamente 5.

Fig. 2-12  Río Humea, Departamento de Meta, Colombia.

Un canal trenzado presenta múltiples subcanales meándricos interconectados (Fig. 2-13). El flujo de agua y sedimentos bajo el cual un canal asume una cierta forma longitudinal es parte del estudio de geomorfología fluvial.

Fig. 2-13   Río Guatiquía, Departamento de Meta, Colombia.

Durante una inundación, los canales naturales pueden desbordarse y asumir temporalmente una parte de la planicie de inundación adyacente (Fig. 2-14). El flujo en canales naturales se clasifica de la siguiente manera: (1) dentro del banco, cuando el flujo se mantiene en el canal principal, o (2) fuera del banco, cuando el flujo se derrama a las planicies adyacentes (Fig. 2-15).

Hidroconsulta S.A.S. Fig. 2-14  Un río que ha desbordado sus bancos.

La Figura 2-15 muestra la variación típica del nivel de la superficie del agua (y) y el tiempo de traslación de la onda de avenida K, en función del grado de inundación. Estas variaciones se deben a cambios en la fricción conforme el nivel de agua aumenta.

Fig. 2-15  Variación típica del nivel de la superficie del agua y el tiempo de traslación de la onda de avenida en función del grado de inundación.

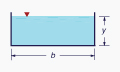
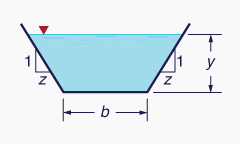
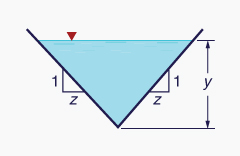
Los canales artificiales se clasifican en: (1) prismáticos, y (2) no prismáticos. Los canales prismáticos tienen una sección transversal constante, ya sea trapezoidal, rectangular o triangular. Los canales trapezoidales son el tipo más común (Fig. 2-16). Los canales rectangulares se utilizan a menudo en flujos sanitarios y aplicaciones de laboratorio. Los canales triangulares normalmente se utilizan en el drenaje urbano y de carreteras.

Fig. 2-16  Canal de alimentación del embalse Tinajones, Lambayeque, Perú.

Los canales no prismáticos son aquéllos en los cuales la sección transversal no es constante. Éstos se utilizan en la transición de una sección transversal a otra, usualmente para tomar en cuenta el cambio de la pendiente del fondo.

Canal hidráulicamente ancho

En canales prismáticos, existen tres formas asintóticas de secciones transversales (Sección 1.3):

1. Hidráulicamente ancho, para el cual el perímetro mojado es constante,

2. Triangular, para el cual el ancho superior es proporcional a la profundidad de flujo (Fig. 1-9), y

3. Inherentemente estable, para el cual el radio hidráulico es constante (Fig. 1-10).

Un canal es hidráulicamente ancho cuando el perímetro mojado P es aproximadamente igual al ancho de la superficie T. Por definición, el radio hidráulico R es igual al área de flujo A dividida entre el perímetro mojado P. Asimismo, la profundidad hidráulica D es igual al área de flujo A dividida entre el ancho de superficie T. Por lo tanto, las siguientes relaciones son válidas para un canal hidráulicamente ancho:

P ≅ T

(2-1)

R ≅ D

(2-2)

En la práctica, un canal se considera hidráulicamente ancho si el ancho de superficie T es mayor o igual a 10 veces la profundidad hidráulica D (Chow, 1959):

T           _____  ≥  10   D

(2-3)

Por definición:

Q = V A

(2-4)

en la cual Q = descarga, A = área de flujo, y V = velocidad media. Así mismo:

A = D T

(2-5)

Por lo tanto:

Q = V D T

(2-6)

y:

q = V D

(2-7)

en la cual q = caudal descarga por unidad del ancho, o gasto unitario [L² T ^-1].

Un canal hidráulicamente ancho puede ser analizado en términos del flujo unitario. Dado un canal hipotético de ancho unitario, el perímetro mojado es una constante: P = T = 1. Por lo tanto, un canal hidráulicamente ancho es aquél para el cual el perímetro mojado es una constante. En la práctica, la mayoría de los canales naturales son hidráulicamente anchos (Fig. 2-17).

Fig. 2-17   El Río Apa, frontera entre Brasil y Paraguay.

Hidráulica de la sección transversal

La relación descarga-área, o curva de gasto, en un canal es:

Q = α Aβ

(2-8)

Los valores asintóticos de β son (Sección 1.3):

1. β = 5/3 para un canal hidráulicamente ancho con el factor de fricción de Manning,

2. β = 3/2 para un canal hidráulicamente ancho con el factor de fricción de Chezy,

3. β = 4/3 para un canal triangular con el factor de fricción de Manning,

4. β = 5/2 para un canal triangular con el factor de fricción de Chezy, y

5. β = 1 para un canal inherentemente estable.

En los canales trapezoidales, los valores de β varían entre aquéllos para los canales hidráulicamente anchos y los triangulares. Los valores típicos de β se encuentran aproximadamente en el rango 1.35 ≤ β ≤ 1.65 (Fig. 2-18) (Ponce y Windingland, 1985).

Fig. 2-18   El Canal San Luis, cerca de Coalinga, en el Valle Central de California.

Profundidad de flujo y profundidad de la sección de flujo

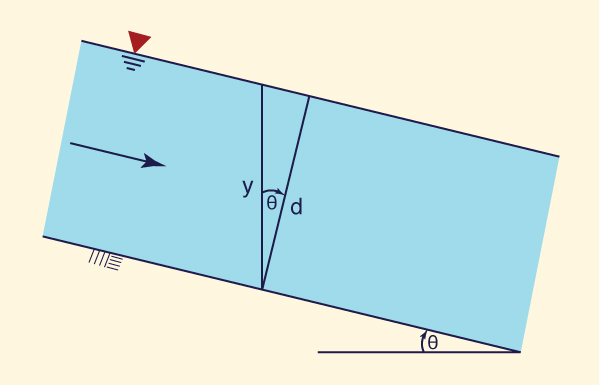
Hay dos profundidades características en el flujo en canales (Fig. 2-19):

1. La profundidad de flujo y, y

2. La profundidad de la sección de flujo d.

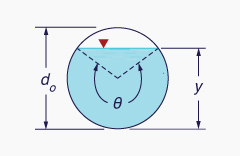
La profundidad de flujo y es la distancia vertical desde la superficie libre hasta el punto más bajo de la sección transversal. La profundidad de la sección de flujo d es la distancia, normal a la dirección del flujo, medida desde la superficie libre hasta el punto más bajo de la sección transversal.

Fig. 2-19   Profundidad de flujo y y profundidad de la sección de flujo d.

La relación entre la profundidad de flujo y y la profundidad de la sección de flujo d es:

d = y cos θ

(2-9)

Geometría de la sección transversal

La Tabla 2-1 muestra la geometría de la sección transversal para cuatro secciones comúnmente usadas.

Tabla 2-1   Geometría de la sección transversal para cuatro secciones comúnmente usadas.
Sección (Haga click en la figura para ampliar)	Área A	Perímetro mojado P	Ancho de superficie T	Radio hidráulico R	Profundidad hidráulica D
	by	b + 2y	b	by __________ b + 2y	y
	(b + zy )y	b + 2y (1 + z 2)1/2	b + 2zy	(b + zy )y ____________________ b + 2y (1 + z 2)1/2	(b + zy )y ____________ b + 2zy
	zy2	2y (1 + z 2)1/2	2zy	zy _______________ 2 (1 + z 2)1/2	y ___ 2
	(θ - sin θ) do2 ________________ 8	θ do ______ 2	do sin (θ/2)	(θ - sin θ) do ________________ 4 θ	(θ - sin θ) do ________________ 8 sin (θ/2)

2.3  DISTRIBUCIÓN DE VELOCIDADES

[Medición de Velocidades]   [Coeficientes de Distribución de Velocidades]   [Distribución de Presiones]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Tipos de Canales]   [Geometría de Canales]

La velocidad media del flujo en un canal es:

Q V  =  _____            A

(2-10)

Las velocidades locales tienden a variar ampliamente. Los perfiles de velocidad vertical varían desde cero en el fondo (la condición de no deslizamiento a nivel del fondo) a valores ligeramente mayores a la media cerca de la superficie del agua (Fig. 2-20).

Fig. 2-20   Esquema del perfil vertical de velocidades.

Las velocidades transversales también tienden a variar, desde cero en los límites laterales a valores máximos cerca del centro del canal (Fig. 2-21). En los canales con meandros, o canales de alineación curva, las velocidades son mayores a lo largo del exterior de la curva y menores en el interior. Sin embargo, para canales hidráulicamente anchos, los costados tienen poca influencia sobre el flujo. En este caso, el flujo se considera bidimensional en las dimensiones longitudinal y vertical.

Fig. 2-21   Curvas típicas de igual velocidad (isotacas) para varias formas de canal (Chow, 1959).

Asumiendo una velocidad media V (Ec. 2-10) se simplifica aún más el flujo, convirtiéndose en una declaración unidimensional en la dirección longitudinal. Este supuesto es aplicable a canales relativamente rectos, en los cuales el flujo permanece dentro de los bancos. El supuesto unidimensional es también aplicable a los canales de meandros con sinuosidades pequeñas y desbordamientos limitados. Sin embargo, la hipótesis unidimensional es insuficiente para canales de gran sinuosidad y/o flujos con grandes desbordamientos (Fig. 2-22).

Fig. 2-22   Ejemplo de canal sinuoso:  Río Meta, Colombia.

2.4  MEDICIÓN DE VELOCIDADES

[Coeficientes de Distribución de Velocidades]   [Distribución de Presiones]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Tipos de Canales]   [Geometría de Canales]   [Distribución de Velocidades]

Las mediciones de velocidad son hechas utilizando medidores de corriente, denominados correntómetros. Éstos miden la velocidad de flujo mediante el conteo del número de revoluciones por segundo del rotor. La rotación puede ser alrededor de un eje vertical, como en el medidor de copa, o alrededor de un eje horizontal, como en el medidor de hélice.

Los correntómetros son ampliamente utilizados en la práctica. El correntómetro Price, el cual tiene seis copas montadas en un eje vertical, es el más común (Fig. 2-23). La velocidad de flujo es proporcional a la velocidad angular del rotor, y se determina contando el número de revoluciones por segundo y consultando la tabla de calibración.

Servicio Geológico de los EE.UU. Fig. 2-23   El correntómetro Price.

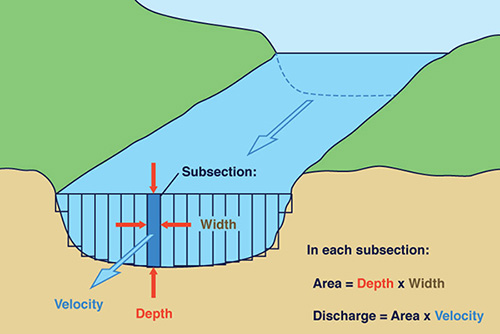
Mediciones de descarga o caudal. La medición del flujo de la corriente en una sección transversal se efectúa determinando el área y la velocidad media para la sección dada. La sección transversal debe ser perpendicular al flujo, y la velocidad media debe basarse en un número suficiente de mediciones de velocidad a lo ancho de la sección.

En el procedimiento típico, se hacen varios sondeos de profundidad, por lo general de 20 a 30 (Fig. 2-24). Cada sondeo está asociado a una sección parcial de la corriente. La sección parcial es un rectángulo de profundidad igual a la de la medición, y de ancho igual a la mitad de la distancia entre las dos verticales adyacentes. En cada vertical se hacen las siguientes observaciones:

1. La profundidad de flujo, y

2. La velocidad medida por el correntómetro en uno o dos puntos en la vertical.

U.S. Geological Survey Fig. 2-24   Procedimiento para el aforo de la descarga o caudal.

En el método de dos puntos, el correntómetro se coloca a 0.2 y 0.8 de la profundidad de flujo, medida a partir de la superficie del agua. Entretanto, en el método de un solo punto, el correntómetro se coloca a 0.6 de la profundidad. El promedio de las velocidades a las profundidades de 0.2 y 0.8, o la velocidad a la profundidad de 0.6 se toma como la velocidad media. El método de un solo punto se recomienda cuando la medición de dos puntos es impráctica; por ejemplo, en corrientes muy poco profundas.

Para cada sección parcial, la descarga se calcula como sigue:

q =  v a

(2-11)

en la cual q = descarga, v = velocidad media, y a = área de flujo. La descarga total Q es la suma de los flujos de todas las secciones parciales.

Los correntómetros Price tipo AA y A se utilizan para mediciones de velocidad de dos puntos en corrientes con profundidades de flujo por encima de 0.75 m, y para las mediciones de un punto en corrientes con profundidades de 0.45 a 0.75 m. El correntómetro pigmeo se utiliza para mediciones en corrientes poco profundas o aforos de laboratorio, con profundidades de 0.10 a 0.45 m.

Las técnicas de medición con correntómetro varían con la profundidad de la corriente. Si la corriente puede ser vadeada, el medidor se fija a una varilla graduada. Si la corriente es muy profunda, el medidor se suspende en un cable y se mantiene en el agua con un contrapeso. Existen contrapesos de diversos tamaños, desde 6.8 kg a 135 kg. Las mediciones que utilizan cables de suspensión son realizadas desde puentes, teleféricos, o lanchas (Fig. 2-25). Para los contrapesos más pesados o cuando se utiliza un barco, puede ser necesario el uso de un cabrestante (winche).

Fig. 2-25   Estación de sondeo de caudal USGS, Campo Creek en Campo Road, Condado de San Diego, California.

2.5  COEFICIENTES DE DISTRIBUCIÓN DE VELOCIDADES

[Distribución de Presiones]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Tipos de Canales]   [Geometría de Canales]   [Distribución de Velocidades]   [Medición de Velocidades]

Debido a la distribución no uniforme de velocidades en una sección transversal, la verdadera carga de velocidad h_v es mayor que la carga de velocidad calculada en base a la velocidad media V. La verdadera carga de velocidad es:

V 2 hv  =  α  ____                2g

(2-12)

en la cual α es el coeficiente de energía, o coeficiente de Coriolis. Los valores de α varían entre 1.03 y 1.36 para los canales prismáticos relativamente rectos. Los valores más altos corresponden a los canales más pequeños y los valores más bajos a los canales más grandes.

El momentun también requiere de una corrección debido a las velocidades no uniformes (Fig. 2-26). La verdadera expresión de flujo de momentun (fuerza) es:

F =  β ρ Q V

(2-13)

en la cual β es el coeficiente de momentun, o coeficiente de Boussinesq; y ρ = densidad de la masa del agua. Los valores de β varían entre 1.01 y 1.12 para canales prismáticos relativamente rectos.

Los valores de α y β son ligeramente mayores de 1, siendo α siempre mayor que β. Para los canales de sección transversal compuesta, α y β fácilmente pueden alcanzar valores de hasta 1.6 y 1.2, respectivamente (Figs. 2-26 y 2-27). En los canales de alineamiento irregular, α y β pueden variar en forma considerable. Valores de β > 2 han sido observados en casos extremos (Chow, 1959).

Fig. 2-26  Una sección transversal de canal compuesto, la cual presenta un alto coeficiente de Coriolis α.

El coeficiente de Coriolis

Asumiendo:

• A = área total de la sección transversal                 ... [L²]

• V = velocidad media de flujo en la sección transversal                 ... [L T ^-1]

• ΔA = área parcial                 ... [L²]

• v = velocidad en el área parcial ΔA                 ... [L T ^-1]

La velocidad media es:

Σ v ΔA V  =  ____________                 ... [L T -1]              Σ ΔA

(2-14)

Por lo general, la energía es la fuerza desarrollada a lo largo de una distancia, o fuerza por distancia:

E  =  ∫ F ds  =  F L                 ... [F L]

(2-15)

La energía cinética correspondiente al área total A es igual al producto de la masa M, por la aceleración, por la distancia:

1 E  =  ____ M V 2                ... [M L 2 T -2]            2

(2-16)

La energía cinética para el área parcial ΔA es:

1 ΔE  =  ____ m v 2                 ... [M L 2 T -2]               2

(2-17)

La carga de velocidad a través de ΔA es igual a la energía cinética dividida por el peso, en el cual peso = mg:

v 2 hv  =  ______                 ... [L]             2 g

(2-18)

El flujo volumétrico a través de ΔA es:

ΔQ  =  v ΔA                 ... [L 3 T -1]

(2-19)

El flujo del peso a través de ΔA es:

Δ(WF)  = γ v ΔA                 ... [F T -1]

(2-20)

en la cual γ = peso específico del agua.

El flujo de energía cinética a través de ΔA es igual al producto de la energía cinética por unidad de peso h_v (Ec. 2-18) por el flujo del peso Δ(WF) (Ec. 2-20):

γ v 3 ΔA Δ(EF)  =  ___________                 ... [F L T -1]                         2 g

(2-21)

La suma de los flujos de energía cinética para todas las áreas parciales es:

γ v 3 ΔA ∑ Δ(EF)  =  ∑ ___________                 ... [F L T -1]                                 2 g

(2-22)

El flujo de energía cinética a través del área total A, basado en la velocidad media V, es:

γ V 3 A (EF)  =  α   ___________                 ... [F L T -1]                          2 g

(2-23)

Igualando las Ecuaciones 2-22 y 2-23, y resolviendo para el coeficiente de energía de Coriolis se obtiene:

Σ v 3 ΔA α  =  _____________                                 V 3 A

(2-24)

El coeficiente de Boussinesq

El flujo de masa J  a través del área total A es igual a la densidad de la masa ρ por el flujo volumétrico total Q = V A:

J  =  ρ V A                 ... [M T -1]

(2-25)

El flujo de masa a través del área parcial ΔA es igual a la densidad de la masa ρ por el flujo volumétrico parcial ΔQ = v ΔA:

ΔJ  =  ρ v ΔA                 ... [M T -1]

(2-26)

En general, el momentun M es igual a la fuerza integrada a lo largo de un período de tiempo, y a su vez es igual a la masa por la velocidad:

M  =  ∫ F dt  =  m V                 ... [M L T -1 ]

(2-27)

El flujo de momentun, o la fuerza F, es igual al flujo de masa por la velocidad. Así, el flujo de momentun a través del área parcial ΔA es:

ΔF  =  ρ v 2 ΔA                 ... [F = M L T -2]

(2-28)

La suma de todos los flujos de momentun, o la suma de las fuerzas para todas las áreas parciales es:

∑ ΔF  =  ∑ ρ v 2 ΔA                 ... [F]

(2-29)

El flujo de momentun, o la fuerza F, a través del área total es:

F  =  β ρ V 2 A                 ... [F]

(2-30)

Igualando las ecuaciones 2-29 y 2-30, y resolviendo para el coeficiente de momentun de Boussinesq se obtiene:

Σ v 2 ΔA β  =  _____________                                 V 2 A

(2-31)

Fig. 2-27   Un río mostrando un nivel alto de inundación, con un valor alto del coeficiente de Boussinesq β.

Formulaciones aproximadas de α y β

Las Ecs. 2-24 y 2-31 son bastante precisas; sin embargo, requieren de mediciones detalladas de la distribución de velocidades en la sección transversal. Alternativamente, cuando únicamente se conocen la velocidad media V  y la velocidad máxima V_max, las siguientes fórmulas pueden ser utilizadas para calcular valores aproximados de los coeficientes de Coriolis y Boussinesq (Chow, 1959):

Vmax ε  =  ________  -  1                              V

(2-32)

Asumiendo una distribución logarítmica de velocidades:

α  =  1  +  3ε 2  -  2ε 3

(2-33)

β  =  1  +  ε 2

(2-34)

Asumiendo una distribución lineal de velocidades:

α  =  1  +  ε 2

(2-35)

ε 2 β  =  1  +  _____                    3

(2-36)

2.6  DISTRIBUCIÓN DE PRESIONES

[Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Tipos de Canales]   [Geometría de Canales]   [Distribución de Velocidades]   [Medición de Velocidades]   [Coeficientes de Distribución de Velocidades]

La distribución de presiones a lo largo de la profundidad de flujo varía con la forma del fondo del canal en relación con la forma de la superficie del agua. Hay tres casos posibles: (1) flujo paralelo, (2) flujo curvilíneo convexo, y (3) flujo curvilíneo cóncavo.

Flujo paralelo

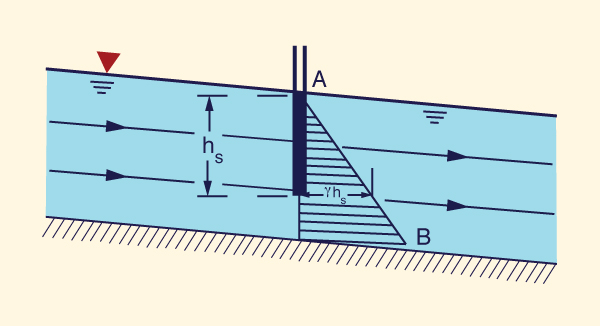
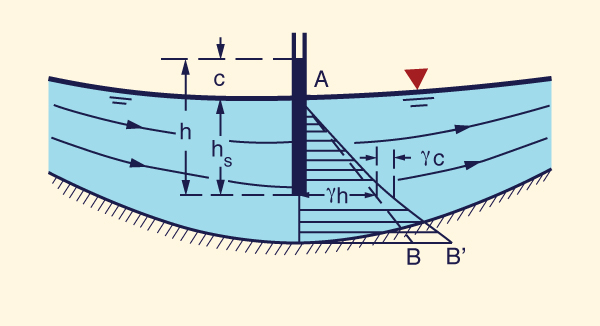
Bajo flujo paralelo, el fondo del canal es relativamente recto y puede ser: (a) paralelo a la superficie del agua, como en el caso del flujo uniforme (Fig. 2-28), o (b) aproximadamente paralelo a la superficie del agua, como el flujo gradualmente variado. En estos casos, la distribución de presiones es hidrostática y la presión varía como una función lineal de la profundidad, como muestra la línea AB de la Fig. 2-28. En la profundidad parcial de flujo h_s, la presión es: p_s = γ h_s. Es decir, un piezómetro situado a la profundidad parcial h_s se elevará a la superficie del agua.

Fig. 2-28   Flujo paralelo.

En la práctica, tanto el flujo uniforme como el flujo gradualmente variado tienen una distribución hidrostática de presiones (Fig. 2-29). Esta distribución se caracteriza por tener velocidades y aceleraciones nulas o despreciables en la dirección normal al flujo.

Fig. 2-29   Flujo uniforme en un canal prismático.

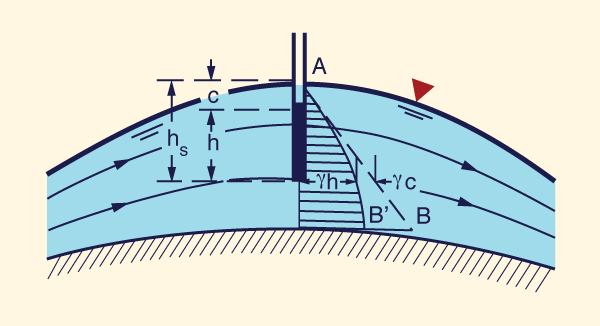
Flujo curvilíneo convexo

En el flujo curvilíneo convexo, la forma del fondo del canal es marcadamente curva, mostrando un perfil convexo en el plano vertical (Fig. 2-30). En este caso, la distribución de presiones no es hidrostática. La presión a lo largo de la profundidad varía en forma no lineal con la profundidad parcial de flujo, como muestra la curva AB' de la Fig. 2-30. Un piezómetro situado en la profundidad parcial h_s ascenderá a una elevación comprendida entre h_s y la superficie del agua. La carga piezométrica real es: h = h_s - c. El valor de c es negativo debido a que la fuerza centrífuga apunta hacia arriba, reduciendo la acción de la gravedad.

Fig. 2-30   Flujo curvilíneo convexo.

En la práctica, el flujo rápidamente variado, por ejemplo, el flujo sobre la cresta de un aliviadero conopial (ogee), tiene una distribución no hidrostática de presiones (Fig. 2-31). Esta distribución se caracteriza por tener grandes velocidades y aceleraciones en la dirección normal al flujo.

Fig. 2-31   Aliviadero de emergencia, Presa El Capitán, Condado de San Diego, California.

Flujo curvilíneo cóncavo

En el flujo curvilíneo cóncavo, la forma del fondo del canal es marcadamente curva, mostrando un perfil cóncavo en el plano vertical (Fig. 2-32). En este caso, la distribución de presiones no es hidrostática. La presión a lo largo de la profundidad varía como una función no lineal de la profundidad parcial de flujo, como muestra la curva AB' de la Fig. 2-32. Un piezómetro situado en la profundidad parcial h_s ascenderá a una elevación mayor que la elevación de la superficie del agua. La carga piezométrica real es: h = h_s + c. El valor de c es positivo porque la fuerza centrífuga apunta hacia abajo, sumándose a la acción de la gravedad.

Fig. 2-32   Flujo curvilíneo cóncavo.

En la práctica, el flujo rápidamente variado, por ejemplo, el flujo en el pie de un aliviadero, cuenta con una distribución no hidrostática de presiones (Fig. 2-33). Esta distribución se caracteriza por tener grandes velocidades y aceleraciones en la dirección normal al flujo.

Fig. 2-33   Flujo curvilíneo cóncavo en el pie del aliviadero de la Presa Cresta, sobre el Río North Fork Feather, California.

La carga de presión centrífuga c puede calcularse aproximadamente como sigue:

• La fuerza centrífuga es igual a la masa por la aceleración centrífuga (f = m × a).

• La presión centrífuga p_c es igual a la masa por unidad de área por la aceleración centrífuga.

• La carga de presión centrífuga c es igual a la presión centrífuga dividida por el peso específico del agua (γ).

La masa por unidad de área es:

Masa/área  =  ρ (Volumen/área)  =  ρ d  =  (γ/g) d                 ... [M L -2 = F T 2 L -3]

(2-37)

en la cual d = profundidad de flujo.

La aceleración centrífuga es:

V 2 a  =  ______                 ... [L T -2]             r

(2-38)

.

en la cual r = radio de curvatura de las líneas de flujo.

Por lo tanto, la presión centrífuga es igual a la Ec. 2-37 por la Ec. 2-38:

γd      V 2 pc  =  _____ _____                 ... [F L -2]             g        r

(2-39)

y la carga de presión centrífuga es:

d      V 2 c  =  ____ _____                 ... [L]           g      r

(2-40)

El valor de c es negativo para el flujo curvilíneo convexo y positivo para el cóncavo (Fig. 2-34).

Fig. 2-34   Flujo curvilíneo cóncavo (salto de esquí), Aliviadero de la presa Tucurui, Para, Brasil.

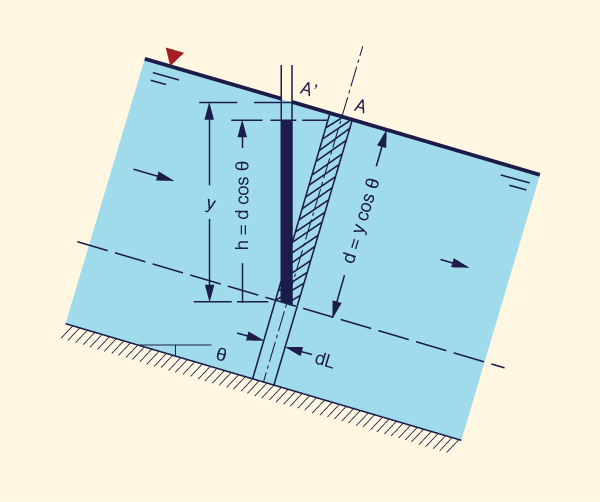
Efecto de la pendiente en la distribución de presiones

La Figura 2-35 muestra un esquema de la distribución de presiones en un canal de pendiente θ muy pronunciada. Observese lo siguiente:

1. El peso del elemento sombreado es:  γ d [dL (1)] = γ y cosθ [dL (1)]

2. La presión ejercida por el elemento sombreado es:  γ d cosθ = γ y cos²θ

3. La carga de presión hidrostástica es:

   h = d cos θ = y cos2θ                 ... [L]

   (2-41)

Para un canal de poca pendiente, h ≅ y, y la profundidad vertical y puede ser utilizada para estimar la carga de presión h. Sin embargo, en un canal de pendiente muy pronunciada, la diferencia puede ser considerable.

Una pendiente de 10% (es decir, una pendiente igual a 0.1) corresponde a un ángulo θ = 5.7°, para el cual cos² (5.7°) = 0.99. Por lo tanto, para una pendiente mayor del 10% se produce un error mayor al 1% al reemplazar la carga de presión h por la profundidad vertical y. Un canal de pendiente pronunciada es aquél que tiene una pendiente mayor al 10%.

Fig. 2-35   Distribución de presiones en un canal de pendiente pronunciada.

En la práctica, un canal de pendiente pronunciada tiene velocidades altas, lo que puede llevar a la oclusión de aire. Esto produce un aumento en volumen y profundidad, y a su vez a una disminución de densidad. Por lo tanto, la presión calculada por la Ec. 2-41 puede ser un poco mayor que el valor real.

PREGUNTAS

[Problemas]   [Bibliografía]   •   [Arriba]   [Tipos de Canales]   [Geometría de Canales]   [Distribución de Velocidades]   [Medición de Velocidades]   [Coeficientes de Distribución de Velocidades]   [Distribución de Presiones]

1. ¿Qué es una rápida?

2. ¿Qué es un acueducto?

3. ¿Qué es una alcantarilla?

4. ¿Qué es potamología?

5. ¿Qué es la sinuosidad en los ríos?

6. ¿Qué es un canal hidráulicamente ancho?

7. ¿Cuál es relación de ancho de superficie a profundidad hidráulica para que un canal pueda ser considerado hidráulicamente ancho?

8. ¿Cuál es el rango típico del exponente β para canales trapezoidales?

9. ¿Cuál es el tipo más común de correntómetro?

10. ¿Por qué la carga de velocidad real es mayor que la carga de velocidad calculada en base a la velocidad media?

11. ¿Cuál es la diferencia entre energía y momentun?

12. ¿Cómo varía la distribución vertical de presiones en el flujo paralelo?

13. ¿Cómo varía la distribución vertical de presiones en el flujo curvilíneo convexo?

14. ¿Cómo varía la distribución vertical de presión en el flujo curvilíneo cóncavo?

15. ¿Qué es un canal de pendiente pronunciada?

PROBLEMAS

[Bibliografía]   •   [Arriba]   [Tipos de Canales]   [Geometría de Canales]   [Distribución de Velocidades]   [Medición de Velocidades]   [Coeficientes de Distribución de Velocidades]   [Distribución de Presiones]   [Preguntas]

1. ¿Cuál es la descarga por unidad de ancho si la descarga es de 24 m³/s y el ancho de superficie del canal es T = 8 m?

2. Dados el factor de la curva de gasto α = 0.4, el exponente β = 1.55, y el área de flujo A = 45.6 m². ¿Cuál es la descarga Q?

3. Dado el diámetro de una alcantarilla d_o = 1 m. ¿Cuál es el área de flujo correspondiente a θ = 300°? (Ver la Tabla 2-1).

4. ¿Cuál es la fuerza F desarrollada por una descarga Q = 10 pies³/s a una velocidad V = 1 pie/s, en una sección transversal con coeficiente de Boussinesq β = 1.05?

5. Una corriente con área de flujo A = 100 m² está dividida en tres secciones: (1) sección de la izquierda, fuera del banco, con 20% del área total de flujo y velocidad de 0.2 m/s; (2) sección central, dentro del banco, con 70% del área total de flujo y velocidad de 1 m/s; y (3) sección de la derecha, fuera del banco, con 10% del área total de flujo y velocidad de 0.1 m/s. Calcular el coeficiente de Coriolis α y el coeficiente de Boussinesq β.

   Fig. 2-36   Una sección transversal compuesta.

6. Calcular los coeficientes de distribución de velocidades para los siguientes datos de un canal, con área total de flujo A = 2768 pies².

   Incremento	Velocidad v (pies/s)	Área parcial de flujo ΔA (%)
   1	3.5	0.5
   2	4.0	2.9
   3	4.5	10.3
   4	5.0	23.5
   5	5.5	52.7
   6	6.0	10.1

   Compare los resultados con los de las fórmulas aproximadas.

7. Un aliviadero está diseñado para un caudal unitario q = 5 m²/s y una profundidad de flujo d = 0.5 m. ¿Cuál es el radio de curvatura mínimo de la sección transversal necesario para asegurar que la presión no baje a un nivel menor del 50% de la hidrostática?

BIBLIOGRAFÍA

•   [Arriba]   [Tipos de Canales]   [Geometría de Canales]   [Distribución de Velocidades]   [Medición de Velocidades]   [Coeficientes de Distribución de Velocidades]   [Distribución de Presiones]   [Preguntas]   [Problemas]

Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, New York.

Ponce, V. M., y D. Windingland. 1985. Kinematic shock: Sensitivity analysis. Journal of Hydraulic Engineering, ASCE, Vol. 111, No. 4, April, 600-611.