4.1  FLUJO CRÍTICO

[Cálculo del Flujo Crítico]   [Control del Flujo Crítico]   [Vertederos de Pared Delgada]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]

En el flujo en canales, dos valores característicos describen el estado de flujo (Sección 1.3):

1. El flujo crítico, el cual describe el flujo permanente para el número de Froude F = 1, y

2. El flujo neutralmente estable, el cual describe el inicio de la inestabilidad de flujo, el cual ocurre para el número de Vedernikov V = 1.

La relación V/F representa dos propiedades importantes:

1. El tipo de fricción, y

2. La forma de la sección transversal.

La curva de gasto, Ec. 1-4 se repite aqui:

Q = α Aβ

(4-1)

en la cual α = coeficiente, y β = exponente. El exponente β es (Sección 1.3):

V β  = 1  +   _____                    F

(4-2)

Los valores del número de Froude F correspondientes a los valores del número de Vedernikov V = 1, es decir, los valores de F_ns, se muestran en la Tabla 1-1.

Criterio del Flujo Crítico

El flujo crítico ocurre bajo las siguientes condiciones (Fig. 4-1):

• Para cierto flujo Q, cuando la energía específica E es mínima.

• Para cierta energía específica E, cuando la descarga Q es máxima.

• Para cierto flujo Q, cuando la fuerza específica F es mínima.

• Para cierta fuerza específica F, cuando la descarga Q es máxima.

• Cuando la velocidad de flujo media u es igual a la celeridad relativa w de las perturbaciones superficiales pequeñas, es decir, ondas dinámicas (Sección 1.3).

• Cuando la carga de velocidad h_v es igual a la mitad de la profundidad hidráulica D.

• Cuando el número de Froude F  es igual a 1.

Fig. 4-1  Flujo crítico sobre el vertedero de emergencia, Reservorio Turner, Condado de San Diego, California.

La condición del flujo crítico representa el límite entre el flujo subcrítico, para el cual F < 1, y el flujo supercrítico, para el cual F > 1.

Las ondas dinámicas en el flujo de canales tienen dos componentes: (1) primario, y (2) secundario (Ponce and Simons, 1977).

Las ondas primarias viajan con velocidades absolutas:

v1 = u  +  w

(4-3)

Las ondas secundarias viajan con velocidades absolutas:

v2 = u  -  w

(4-4)

Mientras que las ondas primarias siempre viajan en dirección aguas abajo, las ondas secundarias pueden viajar en dirección aguas arriba o aguas abajo, dependiendo de las condiciones del flujo. En el flujo subcrítico, w > u, y las ondas secundarias son capaces de viajar en dirección aguas arriba. En el flujo supercrítico, w < u, y las ondas secundarias no pueden viajar en dirección aguas arriba, por lo que siempre viajan aguas abajo. En la práctica, esto significa que el flujo subcrítico es controlado desde aguas abajo, ya que las perturbaciones superficiales son capaces de viajar en dirección aguas arriba. Por el contrario, el flujo supercrítico no puede ser controlado desde aguas abajo, debido a que las perturbaciones superficiales no son capaces de viajar en dirección aguas arriba. El flujo supercrítico siempre es controlado desde aguas arriba.

El flujo crítico puede ocurrir de dos maneras:

1. A lo largo del canal, bajo flujo uniforme, el cual se conoce como flujo uniforme crítico. La pendiente del canal donde se presenta el flujo uniforme crítico se conoce como la pendiente crítica.

2. En una sección transversal específica, bajo el flujo gradualmente variado aguas arriba y aguas abajo, en lo que se conoce como la sección transversal crítica. [En realidad, en la proximidad de la sección transversal del flujo crítico, el flujo puede ser rápidamente variado (Sección 3.3)]. En una sección transversal crítica, la profundidad de flujo se conoce como la profundidad crítica (Fig. 4-2).

Fig. 4-2   Flujo crítico sobre un vertedero natural formado después de la degradación del arroyo al lecho rocoso, Aguaje de la Tuna, Tijuana, Baja California, México.

La ecuación de Darcy-Weisbach para el flujo en canales

La ecuación de Darcy-Weisbach para el flujo en canales, Eq. 1-32, se repite aquí por conveniencia (Sección 1.4):

f        D S  =  ___   _____   F 2           8       R

(4-5)

en la cual el número de Froude es:

V F  =  __________            (gD)1/2

(4-6)

Para un canal hidráulicamente ancho, para el cual D ≅ R, la Ec. 4-5 se reduce a:

f        S  =  ___   F 2           8

(4-7)

En el flujo de canales, se utiliza un factor modificado de fricción Darcy-Weisbach f, igual a 1/8 del factor de fricción Darcy-Weisbach convencional f. La ecuación modificada de Darcy-Weisbach para el flujo en canales es:

S  =  f F 2

(4-8)

Significado físico de la pendiente crítica

La pendiente crítica es aquélla para la cual F = 1. La Ec. 4-5 para F = 1 es:

f        D Sc  =  ___   _____             8       R

(4-9)

en la cual S_c = pendiente crítica. La Ec. 4-7 para F = 1 es:

f         Sc  =  ___               8

(4-10)

Además, la Ec. 4-8 para F = 1 es:

Sc  =  f

(4-11)

Las Ecuaciones 4-9 a 4-11 demuestran que el factor de fricción y la pendiente crítica están muy relacionados. La Ec. 4-9 se utiliza para canales de sección transversal arbitraria, mientras que la Ec. 4-10 se utiliza para canales hidráulicamente anchos. La Ec. 4-11 se utiliza cuando se aplica el factor modificado de fricción Darcy-Weisbach f.

En general:

S  =  Sc F 2

(4-12)

en la cual S_c   se puede definir por cualquiera de las Ecs. 4-9, 4-10, o 4-11.

La Ecuación 4-12 es una modificación de la ecuación de Darcy-Weisbach aplicable al flujo en canales. En el flujo uniforme, esta ecuación muestra claramente el concepto de pendiente crítica. En el flujo gradualmente variado, la Ec. 4-12 permite un mayor entendimiento de los límites asintóticos de las curvas de remanso (Sección 7.3).

Relación entre la pendiente de fondo, la pendiente crítica, y el número de Froude La pendiente de fondo es directamente proporcional al número de Froude, cuando la constante de proporcionalidad es la pendiente crítica. La pendiente de fondo es directamente proporcional a la pendiente crítica, cuando la constante de proporcionalidad es el número de Froude. La pendiente crítica es inversamente proporcional al número de Froude, cuando la constante de proporcionalidad es la pendiente del fondo.

Ocurrencia de flujo crítico

Como indica la Ecuación 4-12, el flujo crítico ocurre cuando la descarga es tal que la pendiente crítica (pendiente de fricción) es igual a la pendiente de fondo. Esto es posible en un canal revestido, donde a medida que aumenta la descarga, la pendiente de fricción disminuye hasta coincidir con la pendiente de fondo. Por lo tanto, en un canal prismático artificial, es posible lograr profundidades de flujo críticas, e inclusive supercríticas. Los flujos supercríticos no son comunes, pero tampoco son imposibles. Por ejemplo, en el caso de la fricción de Chezy en los canales hidráulicamente anchos, las ondas de rollo se forman cuando el número de Vedernikov V = 1, el cual corresponde al número de Froude F = 2 (Fig. 1-6 y Tabla 1-1).

La situación es muy diferente en un canal natural, donde el flujo es capaz de interactuar libremente con el fondo del canal, lo cual aumenta la pendiente "actual" o la fricción efectiva. En la práctica, la pendiente de fricción no disminuye hasta coincidir con la pendiente de fondo, por lo cual el flujo permanece subcrítico. De acuerdo a Jarrett (1982), es muy raro que se presente el flujo crítico o supercrítico en un canal natural (Fig. 4-3).

ASCE Fig. 4-3  El río Arkansas, cerca de Buena Vista, Colorado, con F < 1.

4.2  CÁLCULO DEL FLUJO CRÍTICO

[Control del Flujo Crítico]   [Vertederos de Pared Delgada]   [Preguntas]   [Problemas]   [Bibliografía]   •      [Flujo Crítico]

De la Ec. 4-6, el cuadrado del número de Froude es:

V 2 F 2  =  _______               gD

(4-13)

Al sustituir V = Q /A y D = A /T   en la Ec. 4-13, se obtiene:

Q 2 T F 2  =  _______              g A 3

(4-14)

En el flujo crítico, F = 1, por lo cual la Ec. 4-14 se puede expresar de la siguiente manera:

Q 2 Tc ________  -  Ac 3  =  0      g

(4-15)

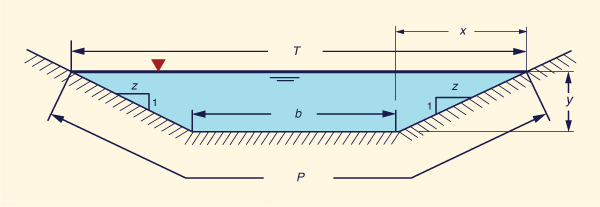
Con referencia a la Fig. 4-4, el ancho de superficie T es:

T = b  +  2zy

(4-16)

El área A del flujo es:

A  =  (b  + x ) y  =  (b  + zy ) y

(4-17)

Fig. 4-4  Ilustración de una sección transversal trapezoidal.

Sustituyendo las Ecs. 4-16 y 4-17 en la Ec. 4-15:

Q 2 (b  +  2zyc) ________________  -  [ (b  + zyc ) yc ] 3  =  0              g

(4-18)

Conociendo g = aceleración de la gravedad, y los datos de descarga Q, ancho de fondo b, y pendiente lateral z [z:H a 1:V, Fig. 4-3], la profundidad crítica y_c se encuentra resolviendo la Ec. 4-18. Además:

Tc = b  +  2zyc

(4-19)

Ac = (b  + zyc ) yc

(4-20)

Ac Dc  =  ______              Tc

(4-21)

Q Vc  =  ______              Ac

(4-22)

La Ecuación 4-18 se expresa como sigue:

Q 2 (b  +  2zyc) f (yc)  =  _________________  -  [ (b  + zyc ) yc ] 3                           g

(4-23)

La Ecuación 4-23 es la fórmula general para el flujo crítico, aplicable a canales trapezoidales. Para un canal rectangular: z = 0, y para un canal triangular de sección simétrica: b = 0.

Con el fin de simplificar la Ecuación 4-23, se hace el cambio de variable x = y_c , obteniéndose:

Q 2 (b  +  2zx) f (x)  =  ________________  -  [ (b  + zx ) x ] 3                          g

(4-24)

La solución de la ecuación cúbica 4-24 se consigue mediante un procedimiento de prueba y error. En el cuadro que sigue se describe un algoritmo utilizado para calcular la primera raíz de la ecuación.

Profundidad crítica en un canal hidráulicamente ancho

Para un canal hidráulicamente ancho, al igual que para un canal rectangular: Q = qb, y z = 0. Sustituyendo estos valores en la Ec. 4-18 se obtiene una expresión para la profundidad crítica y_c en función de la descarga por unidad de ancho q:

q2 yc  =   ( ____ ) 1/3                g

(4-25)

Ejemplo 4-1. Usando CANAL EN LÍNEA 02, calcular la profundidad de flujo crítico para las siguientes condiciones: Q = 10 m3/s; b = 5 m; z = 1.   CÁLCULO EN LÍNEA. Usando la calculadora CANAL EN LÍNEA 02, se obtiene una profundidad crítica de yc = 0.706 m; y una velocidad crítica de vc = 2.483 m/s.

Ejemplo 4-2. Usando CANAL EN LÍNEA 02, calcular la profundidad de flujo crítico para las siguientes condiciones de flujo Q = 100 ft3/s; b = 12 ft; z = 0.   CÁLCULO EN LÍNEA. Usando la calculadora CANAL EN LÍNEA 02, la profundidad crítica es yc = 1.292 ft; y la velocidad crítica es vc = 6.448 ft/s.

4.3  CONTROL DEL FLUJO CRÍTICO

[Vertederos de Pared Delgada]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Flujo Crítico]   [Cálculo del Flujo Crítico]

En la Ecuación 4-23, la profundidad de flujo crítico es una función de Q, b, y z solamente. Entonces, la profundidad de flujo crítico y el flujo crítico son independientes de la pendiente de fondo y de la fricción. Puede observarse que para F = 1, la pendiente crítica y la pendiente de fondo se cancelan mutuamente. Por lo cual, en el flujo crítico, para una descarga dada, la profundidad de flujo es una constante, independiente de la pendiente.

Cuando la curva de gasto es única, es decir cuando existe solamente una profundidad de flujo para cada descarga, y viceversa, la condición se conoce como control. El control puede ser: (1) control de sección (control transversal), actuando en una sección transversal, o (2) control de canal (control longitudinal), actuando a lo largo del canal.

Las figuras 4-5 a 4-7 muestran tres casos de control de flujo crítico en un canal prismático, actuando bajo las siguientes pendientes: (1) subcrítica, (2) crítica, y (3) supercrítica.

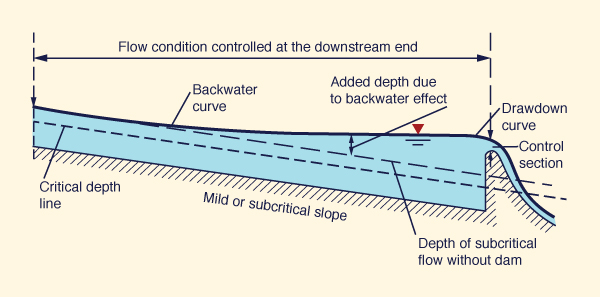
La condición de flujo subcrítico representado en la Fig. 4-5 muestra la existencia del control de la sección crítica solamente en la cresta de la presa aguas abajo, de tal manera que el flujo se controla en el extremo aguas abajo.

Fig. 4-5  Ubicación de la sección de control crítica en el flujo subcrítico (Chow, 1959).

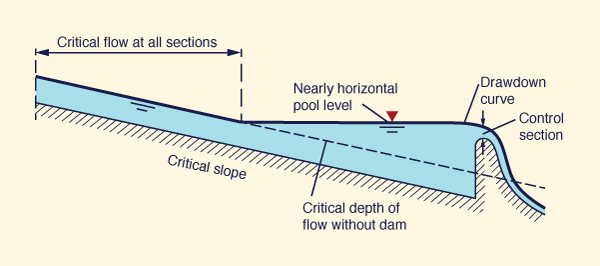
La condición de flujo crítico de la Fig. 4-6 muestra el control crítico en dos puntos: (1) control de la sección en la cresta de la presa aguas abajo, y (2) control del canal a lo largo del canal de pendiente crítica aguas arriba. Se muestra un perfil de remanso, el cual tiene un nivel casi horizontal, el cual conecta a las dos secciones de control de flujo. El flujo se controla en el extremo de aguas abajo.

Fig. 4-6   Ubicación de la sección de control crítica en el flujo crítico (Chow, 1959).

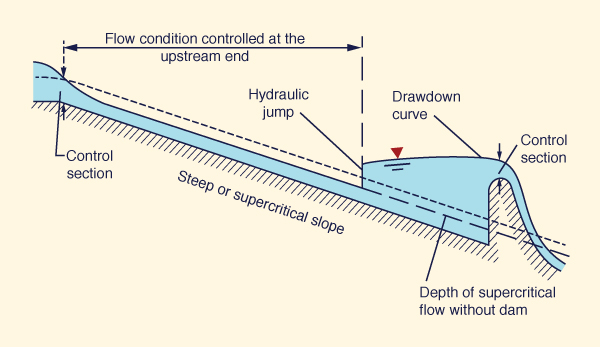
La condición de flujo supercrítico de la Fig. 4-7 muestra control crítico en dos puntos: (1) sección de control en la cresta de la presa aguas abajo, y (2) sección de control en la primera sección aguas arriba del canal supercrítico. El flujo es controlado en ambos extremos, con un salto hidráulico que ocurre cerca del punto medio.

Fig. 4-7  Ubicación de las secciones de control críticas en el flujo supercrítico (Chow, 1959).

El concepto de singularidad de la curva de gasto califica al flujo crítico como un control (de sección o canal). Esto proporciona una manera conveniente de encontrar la descarga en base a la profundidad, y viceversa. Esta propiedad de flujo crítico es útil en las mediciones de flujo.

El control crítico para la medición de flujo se lleva a cabo de dos maneras: (1) flujo en un vertedero (control de sección), y (2) canaleta o medidor de flujo crítico (control de canal). El flujo en un vertedero se describe en la Sección 4.4. El medidor Parshall es un ejemplo típico de medidor de flujo crítico (Fig. 4-8). En condiciones de flujo libre (con baja profundidad aguas abajo), se requiere únicamente una medición para determinar la descarga. Sin embargo, bajo condiciones sumergidas (con alta profundidad aguas abajo), se requiere de dos mediciones.

Fig. 4-8  Medidor Parshall en el humedal construído de Cucuchucho, Michoacán, México.

En un vertedero de cresta ancha, el flujo crítico ocurre cerca de la cresta. La descarga por unidad de ancho es:

q  =  Vc yc

(4-26)

q  =  (gyc)1/2 yc

(4-27)

q  =  (g)1/2 (yc)3/2

(4-28)

Por definición, la profundidad crítica es 2/3 de la carga total H medida sobre la cresta del vertedero:

yc  =  (2/3) H

(4-29)

Sustituyendo la Ec. 4-29 en la Ec. 4-28:

q  =  C H 3/2

(4-30)

en la cual C es un coeficiente de descarga definida como sigue:

C  =  (2/3)3/2 g1/2

(4-31)

En unidades SI, C = 1.704; y en unidades acostumbradas en EE.UU., C = 3.087.

Por diversas razones, un valor de diseño actual C_d puede diferir del valor teórico C. La experiencia ha demostrado que el rango aproximado es: 0.8 ≤ C_d /C ≤ 1.3. La Figura 4-9 muestra un vertedero de cresta ancha para el cual C_d = 1.45 (unidades SI).

En la práctica, H se toma como la elevación de la superficie del agua por encima de la cresta del vertedero. Esto asume que la velocidad de aproximación V_a en una sección localizada suficientemente aguas arriba del vertedero es nula: V_a = 0.

[Ver también Video de Laboratorio:  Vertederos de cresta ancha].

Fig. 4-9  El vertedero de emergencia, de 8000 pies de coronación, en el Lago de Conservación Boerasirie, Guyana.

4.4  VERTEDEROS DE PARED DELGADA

[Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Flujo Crítico]   [Cálculo del Flujo Crítico]   [Control del Flujo Crítico]   [Vertederos de Pared Delgada]

Los vertederos de pared delgada se utilizan para forzar una sección de control en un canal, con el objetivo de medir el flujo. Los vertederos de pared delgada se construyen usando secciones triangulares, trapezoidales, rectangulares.

Vertederos Triangulares

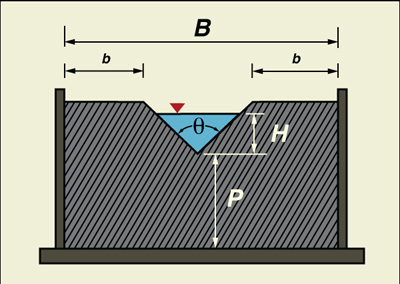
Los vertederos triangulares son de dos tipos: (a) totalmente contraídos, o (b) parcialmente contraídos. La contracción se refiere al tamaño del área de flujo del vertedero en comparación con el tamaño del área de flujo del canal aguas arriba. Un vertedero puede estar sujeto a contracciones tanto verticales como horizontales, dependiendo de su tamaño y diseño. Para que el vertedero sea totalmente contraído, sus extremos deben estar suficientemente lejos de los costados y del fondo del canal (Fig. 4-10). Cuando la contracción es completa, la precisión de la medición se incrementa al obtenerse una sección de control más precisa (una relación única caudal-tirante) muy cerca del vertedero.

Vertedero triangular completamente contraído. El vertedero triangular es un tipo comúnmente usado de vertedero de pared delgada. La contracción completa se produce cuando la distancia b de la ranura al costado del estanque es mayor que 2H. Para un vertedero triangular de 90°, el ancho del flujo a nivel de diseño es igual a 2H. Por lo tanto, se considera que el vertedero es totalmente contraído cuando la relación B/H > 6, es decir, para H/B < 0.167. Un vertedero triangular de 60° se considera totalmente contraído cuando: H/B < 0.194. El criterio práctico del USBR (U.S. Bureau of Reclamation) para un vertedero triangular totalmente contraído es: H/B ≤ 0.2.

Un vertedero se considera parcialmente contraído si no satisface la relación anterior. Por ejemplo, puede ser que el ancho B del canal sea demasiado pequeño en comparación a la carga H. De acuerdo al USBR, el criterio práctico para un vertedero triangular parcialmente contraído es: H/B ≤ 0.4.

Fig. 4-10  Vertedero triangular de pared delgada.

La fórmula para un vertedero triangular totalmente contraído, en unidades acostumbradas en EE.UU. (Q en pies cúbicos por segundo, H en pies), es (USBR Water Manual):

Q = 4.28 Ce tan (θ/2) (H + k)5/2

(4-32)

En la Ecuación 4-32, la descarga Q es una función de la carga hidráulica H y el ángulo θ. El coeficiente de descarga C_e y el coeficiente de corrección de carga k son funciones de θ. El ancho B del canal aguas arriba se utiliza para verificar la contracción completa:   H/B ≤ 0.2.

La fórmula de ajuste polinomial para C_e, con θ en grados, es:

Ce = 0.607165052 - 0.000874466963 θ + 0.0000061039334 θ2

(4-33)

La fórmula para k, con θ en grados, es (LMNO Engineering):

k = 0.0144902648 - 0.00033955535 θ + 0.00000329819003 θ2 - 0.0000000106215442 θ3

(4-34)

El vertedero triangular totalmente contraído debe cumplir las siguientes condiciones:

1. Carga H < 1.25 ft (38 cm).

2. Ancho B > 3 ft (91 cm).

3. Altura P > 1.5 ft (46 cm).

4. Relación b/H ≥ 2.0.

5. Relación carga/ancho H/B ≤ 0.2.

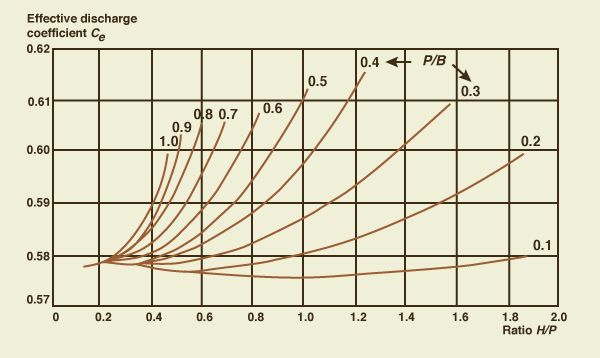
Vertedero triangular parcialmente contraído. Para un vertedero triangular de 90° parcialmente contraído, la Ec. 4-32 se reduce a:

Q = 4.28 Ce (H + 0.0029)5/2

(4-35)

El coeficiente de descarga C_e es función de las relaciones H/P y P/B, como se muestra en la Fig. 4-11.

Fig. 4-11  Variación de Ce como una función de H/P y P/B.

El vertedero triangular de 90° parcialmente contraído debe cumplir las siguientes condiciones:

1. Carga H < 2 ft (61 cm).

2. Ancho B > 2 ft (61 cm).

3. Altura P > 0.33 ft (10 cm).

4. Relación carga/ancho H/B ≤ 0.4.

Ejemplo 4-3. Usando el ENLINEA TRIANGULAR 1, calcular la descarga sobre un vertedero triangular totalmente contraído para las siguientes condiciones: carga H = 1 ft; ancho B = 6 ft; ancho b = 2 ft; ángulo θ = 90°.   CÁLCULO EN LÍNEA. Usando la calculadora ENLINEA TRIANGULAR 1, la descarga es: Q = 2.49 ft3/s.

Vertedero trapezoidal:  Vertedero Cipolletti

Un vertedero Cipolletti estándar es de forma trapezoidal (Fig. 4-12). La cresta y los lados de la placa del vertedero se colocan lo suficientemente lejos del fondo y los lados del canal, con el fin de producir una contracción completa. Los lados se inclinan hacia fuera con una pendiente de 1 horizontal a 4 vertical. El procedimiento del cálculo se encuentra en la Sección 12 del Capítulo 7 del Manual de Medición del Agua USBR.

Fig. 4-12  Vertedero Cipolletti.

La fórmula para el vertedero Cipolletti, en unidades acostumbradas en EE.UU., es:

Q = 3.367 L H 3/2

(4-36)

en la cual L = longitud de la cresta del vertedero, en pies, y H = carga sobre la cresta del vertedero, en pies.

La precisión de las mediciones obtenidas con la Ec. 4-36 es considerablemente menor que la que se obtiene con vertederos triangulares. La precisión del coeficiente de descarga es de ± 5%.

El vertedero Cipolletti está sujeto a las siguientes condiciones:

1. La carga H ≥ 0.2 ft (6.1 cm).

2. La relación P/H ≥ 2.

3. La relación b/H ≥ 2.

La carga H se mide aguas arriba de la cresta a una distancia mayor o igual a 4H.

Vertederos Rectangulares

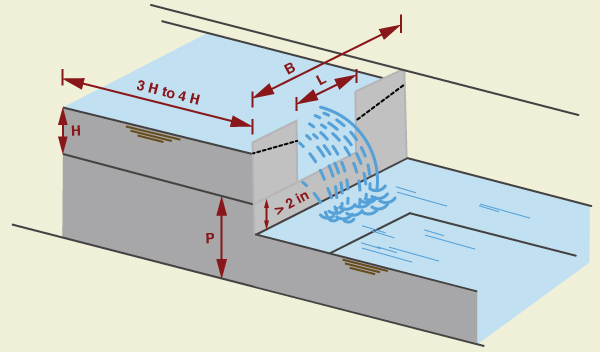
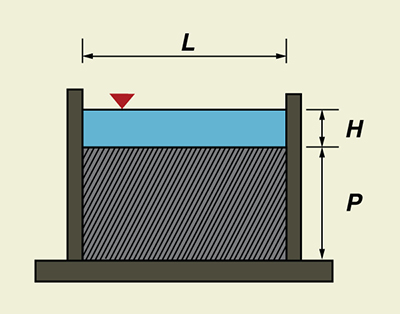
Un vertedero rectangular tiene la forma que se muestra en la Fig. 4-13. Para obtener una contracción completa, la cresta y los lados de la placa del vertedero se colocan a una distancia considerable del fondo y de los lados del canal. El procedimiento de cálculo se muestra en la Sección 6 del Capítulo 7 del Manual de Medición del Agua USBR.

Fig. 4-13  Perspectiva en tres dimensiones de un vertedero rectangular.

La fórmula de Kindsvater-Carter para un vertedero rectangular, en unidades acostumbradas en EE.UU., es:

Q = Ce (L + kb) (H + 0.003)3/2

(4-37)

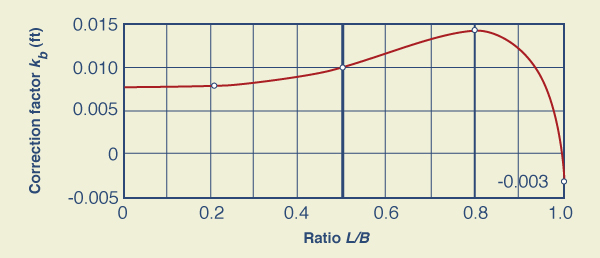
en la cual C_e = coeficiente efectivo de descarga; L = longitud de la cresta del vertedero, en pies, k_b = factor de corrección para obtener la longitud efectiva del vertedero, en pies; H = carga medida sobre la cresta del vertedero, en pies; y Q = descarga, en pies cúbicos por segundo. El valor B es el ancho medio del canal.

El factor de corrección k_b en función de la relación L/B se muestra en la Fig. 4-14.

Fig. 4-14  Factor de corrección kb para la longitud efectiva de un vertedero rectangular.

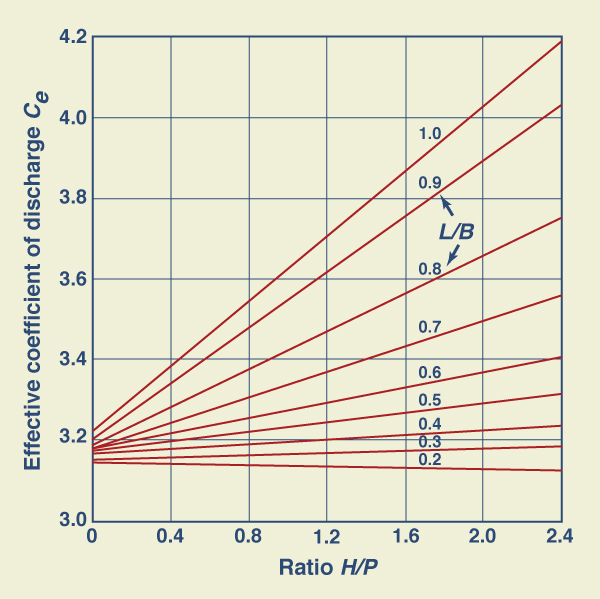
El coeficiente efectivo de descarga C_e incluye efectos de la profundidad relativa y del ancho relativo del canal. Este coeficiente es una función de H/P y L/B, como se muestra en la Fig. 4-15.

Fig. 4-15  Valores de Ce en función de H/P y L/B.

Conociendo los valores H, L, B y P, y las relaciones H/P y L/B, el cálculo se efectúa de la siguiente manera:

1. El factor de corrección k_b es calculado usando la Fig. 4-14.

2. El coeficiente efectivo de descarga C_e es calculado usando la Fig. 4-15.

3. La descarga Q es calculada usando la Ec. 4-37.

La ecuación del vertedero rectangular (Ec. 4-37) está sujeta a las siguientes condiciones:

1. Las relaciones de calibración (Fig. 4-14 y 4-15) han sido desarrolladas considerando flujo rectangular aguas arriba. En el caso de usarse otras formas de sección, para cada carga, el B debe ser el promedio de los anchos de cada sección.

2. La carga H debe ser al menos 0.2 pies (0.061 m).

3. La altura de la cresta P ≥ 4 pulgadas (0.3333 pies, o 0.1015 m).

4. La longitud de la cresta L ≥ 6 pulgadas (0.5 pies, o 0.1524 m).

5. La relación H/P ≤ 2.4.

   La elevación de la superficie del agua en el canal aguas abajo deberá encontrarse por lo menos a 2 pulgadas (5 cm, o 0.05 m) debajo de la cresta del vertedero (Fig. 4-16).

Gary Player Fig. 4-16  Vertedero rectangular en Ash Creek, cerca a New Harmony, Utah.

Vertedero rectangular contraído estándar. La Figura 4-17 muestra un vertedero rectangular contraído estándar. Para obtener una contracción completa, los lados y extremos de la placa de rebose se deben situar a una distancia de los límites del flujo de aguas arriba mayor o igual a 2H. La carga se mide a una distancia aguas arriba del vertedero mayor o igual a 4H. El procedimiento de cálculo se muestra en la Sección 9 del Capítulo 7 del Manual Medición del Agua USBR.

Fig. 4-17  Vertedero rectangular contraído estándar.

La ecuación de Francis es la fórmula para el vertedero rectangular contraído estándar. En las unidades acostumbradas en EE.UU., esta ecuación es:

Q = 3.33 (L - 0.2H ) H 3/2

(4-38)

en la cual Q = descarga, en pies cúbicos por segundo, L = longitud de la cresta del vertedero, en pies, y H = carga en la cresta del vertedero, en pies.

La precisión de las mediciones obtenidas por la Ec. 4-38 es considerablemente menor que la que se obtiene con vertederos triangulares. La precisión del coeficiente de descarga es de ± 5%.

La ecuación 4-38 tiene un coeficiente de descarga constante (3.33), lo que facilita los cálculos. Sin embargo, el coeficiente no permanece constante para una relación de carga-cresta H/L > 1/3, y la descarga real supera la calculada. Los experimentos de Francis se hicieron en vertederos relativamente largos, la mayoría de ellos con longitud de cresta L = 10 pies y cargas en el rango 0.4 pies ≤ H ≤ 1.6 pies, por lo que la ecuación funciona únicamente bajo estas condiciones. Sin embargo los experimentos USBR en vertederos de 6 pulgadas, 1 pie, y 2 pies han demostrado que la ecuación de Francis puede dar buenos resultados en longitudes de cresta L más cortas, siempre y cuando H/L ≤ 1/3.

La ecuación 4-38 está sujeta a las siguientes condiciones:

1. La relación P/H ≥ 2.

2. La relación b/H ≥ 2.

3. La relación  L/H ≥ 3.

Vertedero rectangular suprimido estándar. Un vertedero rectangular sumprimido estándar tiene una cresta horizontal que atraviesa completamente el ancho del canal (Fig. 4-18). Es necesario que la elevación de la cresta sea lo suficientemente alta para asegurar la contracción completa. Las paredes laterales del canal aguas arriba se continúan más allá del flujo sobre el verdedero, para así prevenir una contracción o expansión lateral del flujo de desborde. El procedimiento de cálculo se encuentra en la Sección 10 del Capítulo 7 del Manual de Medición del Agua USBR.

Es necesario asegurar una aereación adecuada en la cresta, debajo de la lámina de desborde. Esto se lleva a cabo colocando rejillas de ventilación debajo de la capa de flujo, en ambos lados del vertedero. Las condiciones adicionales que aseguran la precisión de mediciones en este tipo de vertedero son generalmente las mismas que para las del vertedero rectangular contraído. Sin embargo en este caso no existe la contracción lateral. Además, la altura de la cresta P debe ser mayor o igual a 3H.

Fig. 4-18  Vertedero rectangular suprimido estándar.

La ecuación de Francis es la fórmula para el vertedero rectangular suprimido estándar. En las unidades acostumbradas en EE.UU., esta ecuación es:

Q = 3.33 (L - 0.2H ) H 3/2

(4-39)

en la cual Q = descarga, en pies cúbicos por segundo, L = longitud de la cresta del vertedero, en pies, y H = carga en la cresta del vertedero, en pies.

La precisión del coeficiente de descarga es de ± 5%. La Ecuación 4-39 no debe utilizarse para cargas H < 0.2 pies. Las pequeñas cargas no permiten mediciones de flujo exactas ya que es posible que la capa de flujo sobre la cresta no salte libremente.

La Ecuación 4-39 está sujeta a las siguientes condiciones:

1. Carga H ≥ 0.2 ft.

2. Longitud L ≥ 4 ft.

3. Relación altura-carga P/H ≥ 3.

4. Relación longitud-carga  L/H ≥ 3.

La carga H se mide a una distancia mínima aguas arriba de 4H. Las paredes laterales deben extenderse por lo menos a una distancia 0.3H aguas abajo de la cresta. La lámina de vertido debe estar debidamente ventilada.

Ejemplo 4-4. Usando el ENLINEA ESTÁNDAR SUPRIMIDO, calcular la descarga sobre un vertedero rectangular suprimido estándar bajo las siguientes condiciones: carga H = 0.5 m; longitud L = 5 m; altura P = 2 m.   CÁLCULO EN LÍNEA. Usando la calculadora ENLINEA ESTÁNDAR SUPRIMIDO, la descarga es: Q = 3,250 L/s. Q = 3,250 L/s.

PREGUNTAS

[Problemas]   [Bibliografía]   •   [Arriba]   [Flujo Crítico]   [Cálculo del Flujo Crítico]   [Control del Flujo Crítico]   [Vertederos de Pared Delgada]

1. ¿Por qué el exponente β de la curva de gasto es importante en el flujo de canales?

2. Dada una descarga Q: ¿Cuál es el valor de la energía específica en el flujo crítico?

3. ¿Cuál es la relación entre la carga de velocidad y la profundidad hidráulica bajo el flujo crítico?

4. ¿Cuál es la diferencia entre las ondas primarias y secundarias en el flujo no permanente en canales?

5. ¿Cómo están relacionadas la pendiente del fondo, la pendiente crítica, y el número de Froude en el flujo uniforme?

6. ¿Por qué es poco común tener flujo crítico o supercrítico en un canal natural?

7. La profundidad crítica en un canal hidráulicamente ancho es función de una sola variable. ¿Cuál es esta variable?

8. ¿Cuántos tipos de control existen en el flujo en canales?

9. ¿Bajo qué condición se requieren dos mediciones de nivel en un medidor Parshall?

10. ¿Por qué es necesaria la contracción completa en la medición de flujo con un vertedero de pared delgada?

11. ¿El vertedero Cipolletti es totalmente o parcialmente contraído?

12. ¿Cómo se obtiene la contracción completa en un vertedero rectangular suprimido estándar?

PROBLEMAS

[Bibliografía]   •   [Arriba]   [Flujo Crítico]   [Cálculo del Flujo Crítico]   [Control del Flujo Crítico]   [Vertederos de Pared Delgada]   [Preguntas]

1. Usando la ecuación de Chezy (Ec. 5-10), derivar la fórmula para la pendiente crítica S_c en un canal prismático.

2. Usando la ecuación de Manning (Ec. 5-17 o la Ec. 5-18), derivar la fórmula para la pendiente crítica S_c en un canal prismático.

3. Calcular la descarga teórica sobre un vertedero de cresta ancha de longitud L = 22 pies,, cuando la carga total es H = 1.2 pies. Verificar con CANAL EN LÍNEA 14.

4. Calcular la descarga teórica sobre un vertedero de cresta ancha de longitud L = 8 m, cuando la carga total es H = 0.5 m. Verificar con CANAL EN LÍNEA 14.

5. Calcular la profundidad crítica correspondiente a una descarga q = 1.36 m²/s.

6. Dado un factor de fricción Darcy-Weisbach modificado f = 0.003 y una pendiente de fondo S = 0.002. Calcular el número de Froude.

7. Usar CANAL EN LÍNEA 04 para calcular la pendiente crítica para los siguientes datos del canal: Q = 11 m³/s, b = 1.5 m, z = 1, S = 0.0006, n = 0.013.

8. Usar CANAL EN LÍNEA 04 para calcular la pendiente crítica para los siguientes datos del canal: Q = 35 pies³/s, b = 3 pies, z = 1, S = 0.001, n = 0.015.

9. Usar ONLINE CIPOLLETTI para calcular la descarga de un vertedero Cipolletti (Fig. 4-19), dada la carga H = 1 pie, longitud L = 3.2 pies, altura P = 4 pies, y ancho B = 6 pies.

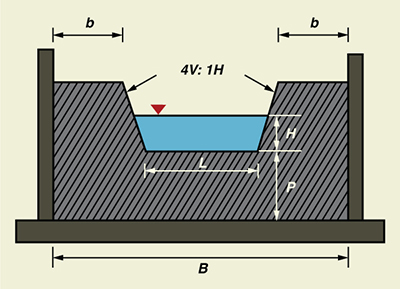
   Fig. 4-19  Vertedero Cipolletti.

10. Usar ONLINE STANDARD CONTRACTED RECTANGULAR para calcular la descarga de un vertedero rectangular contraído estándar (Fig. 4-20), dada la carga H = 0.5 m, longitud L = 3 m, altura P = 3 m, y ancho b = 1.5 m.

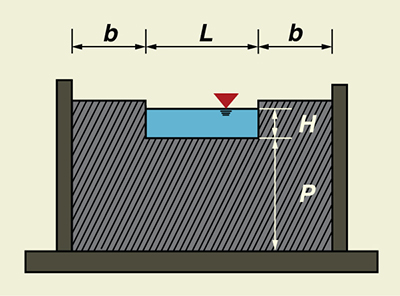
    Fig. 4-20  Vertedero rectangular contraído estándar.

BIBLIOGRAFÍA

•   [Arriba]   [Flujo Crítico]   [Cálculo del Flujo Crítico]   [Control del Flujo Crítico]   [Vertederos de Parede Delgada]   [Preguntas]   [Problemas]

Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, Nueva York.

Jarrett, R. D., 1984. Hydraulics of High-Gradient Streams. ASCE Journal of Hydraulic Engineering, Vol. 110, No. 11, Noviembre, 1519-1539.

Ponce, V, M., y D. B. Simons. 1977. Shallow wave propagation in open-channel flow. Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, Diciembre, 1461-1476.