Victor Miguel Ponce
Julio 2017
1. INTRODUCCIÓN
1.1 Introducción La infraestructura vial de un país constituye el motor principal del desarrollo económico y social de la nación. Esta infraestructura consta de carreteras nacionales, regionales, y locales, las cuales varían en importancia y tamaño, dependiendo del plan nacional de transporte y el tráfico planeado o establecido. Las carreteras se diseñan siguiendo las normas publicadas por los organismos competentes de los gobiernos nacionales, regionales, y locales. El diseño de una carretera o camino incluye los siguientes componentes:
Los diseños geométricos están basados en principios establecidos de la ingeniería de transportes, la cual incluye planeamiento, volumen de tráfico, y la geotecnia relacionada. El diseño de taludes considera criterios de geotecnia. El diseño de obras de drenaje considera criterios de hidrología, hidráulica, y agua subterránea. El diseño adecuado de obras de drenaje vial es muy importante para garantizar la estabilidad, durabilidad, y transitabilidad de una carretera. Se reconoce que la probabilidad P de falla de una estructura vial es finita (P > 0); sin embargo, ésta puede reducirse mediante un análisis exhaustivo de la seguridad de la obra vs el costo asociado. La pregunta a responder es la siguiente: ¿Cuales deben ser las dimensiones de la obra de drenaje con el fin de garantizar un nivel de riesgo previamente establecido? Este manual trata de las consideraciones para el diseño de obras de drenaje de carreteras, incluyendo:
El objetivo es propiciar un mejor diseño de las obras de drenaje
con el fin de reducir y/o minimizar las fallas de carreteras que puedan ser atribuídas a un diseño
hidrológico/hidráulico insuficiente
o defectuoso. Se reconoce que el drenaje insuficiente es la causa más
común de fallas estructurales en los sistemas viales.
Este manual trata procedimientos y metodologías para el análisis, cálculo,
y diseño de obras de
drenaje de carreteras, incluyendo alcantarillas,
puentes, y drenaje longitudinal y transversal, superficial y subterráneo.
El énfasis de esta obra es en conceptos
modernos de hidrología, hidráulica, y transporte de sedimentos.
Acorde con los avances de los tiempos actuales, el manual hace uso de un gran número de calculadoras en línea, las cuales
facilitan el análisis y el cálculo,
optimizando así la experiencia y reduciendo el tiempo requerido para el diseño.
Asimismo, la disponibilidad en línea de este manual en formato HTML facilita grandemente su acceso y visualización, y
por ende, su
corrección, mejora, y ampliación.
Cabe notar que su formato amistoso lo coloca en posición privilegiada
para informar, educar, e instruir a las generaciones presentes y futuras de
profesionales ingenieros
dedicados al planeamiento, diseño, contrucción, conservación y mantenimiento de
carreteras.
2. HIDROLOGÍA
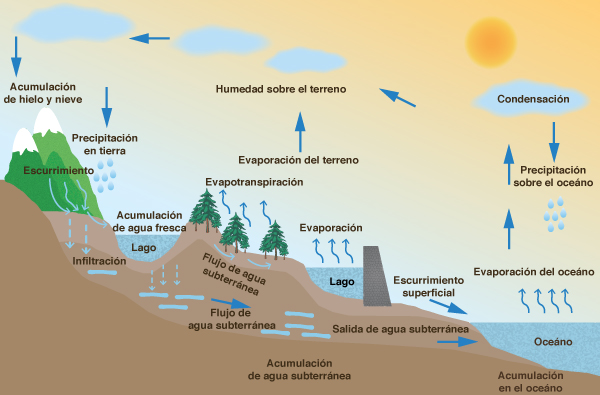
Toda el agua que escurre sobre la Tierra tiene su origen en el ciclo hidrológico.
Éste es un proceso continuo por medio del cual el agua se evapora de los
océanos y es transportada, por gradientes de presiones
atmosféricas, hacia las regiones continentales, donde
se produce su precipitación a la superficie y regresa eventualmente al océano, impulsada esta vez por la fuerza de la gravedad.
La Figura 1 muestra los componentes del ciclo hidrológico.
El drenaje de carreteras tiene como objetivo principal el manejar las aguas del ciclo hidrológico con el fin de reducir y/o eliminar el riesgo de daños a las carreteras y obras accesorias [obras de arte]. Desde el punto de vista de drenaje, la componente más importante del ciclo hidrológico es el escurrimiento, o escorrentía, superficial. El escurrimiento superficial se refiere a la fracción [de tiempo, del ciclo hidrológico] en la cual el agua es transportada sobre el terreno, en contacto directo con éste. En la práctica, el escurrimiento superficial tiene dos manifestaciones bien diferenciadas:
Ambos tipos de escurrimiento son importantes en el drenaje de carreteras. Los flujos sobre el terreno eventualmente se juntan o unifican, formando un flujo en corriente. La situación local determina si el flujo es (a) sobre el terreno, o (b) en corriente. Generalmente, el flujo sobre el terreno tiene profundidades pequeñas (Fig. 2), mientras que el flujo en corriente tiene usualmente profundidades mayores (Fig. 3).
El flujo en corriente puede originarse:
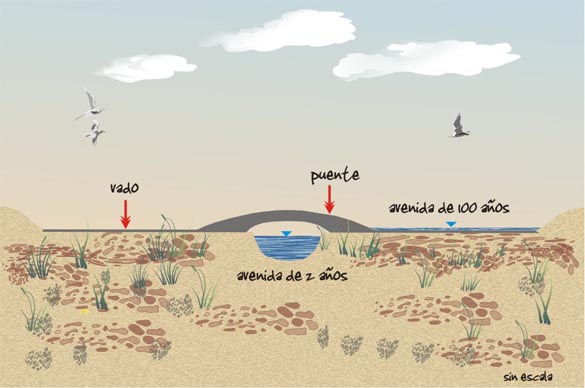
El flujo directo es típicamente rápido, por lo tanto, es muy importante en el drenaje de carreteras. Contrariamente a esto, el flujo indirecto es lento; por lo tanto, es de importancia secundaria en el drenaje. Las corrientes, ya sean naturales o artificiales, se clasifican en: (a) efímeras, (b) intermitentes, y (c) perennes. Las corrientes efímeras las constituyen las quebradas y arroyos, es decir, los cursos de agua predominantemente secos, los cuales conducen flujos solamente durante un evento de lluvia y/o inmediatamente después de éste. Las obras de drenaje se concentran particularmente en las corrientes efímeras, las cuales son capaces de conducir grandes cantidades de agua provenientes de los aguaceros o chubascos. Estos grandes flujos pueden eventualmente poner en peligro la integridad de las obras viales (Fig. 4).
2.2 Difusión del escurrimiento Una consideración importante en el drenaje de carreteras es la difusión del escurrimiento. Ésta se refiere al cálculo de la magnitud de la descarga de diseño. En el análisis hidráulico, el flujo se clasifica en:
La difusión es el mecanismo por medio del cual el flujo no permanente se atenúa en el espacio y en el tiempo, disminuyendo su tamaño por debajo de un valor máximo teóricamente posible. En la práctica, la magnitud de difusión determina el valor de la descarga de diseño. El valor máximo posible Qmax es función de la intensidad de precipitación (intensidad efectiva Ie) y el tamaño de la cuenca (área de drenaje A):
En ausencia de difusión, la descarga o caudal adquiere su valor máximo, dado por la Ec. 1. Contrariamente a esto, en presencia de difusión, la descarga se atenúa, es decir, disminuye su valor por debajo del máximo. El objetivo central de la hidrología del drenaje de carreteras es calcular la magnitud de difusión. Este cálculo depende si el flujo es a través de:
2.2.1 Difusión a través de un embalse
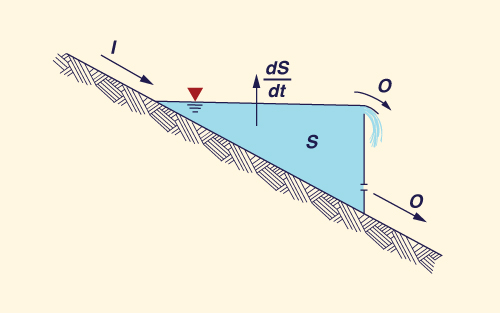
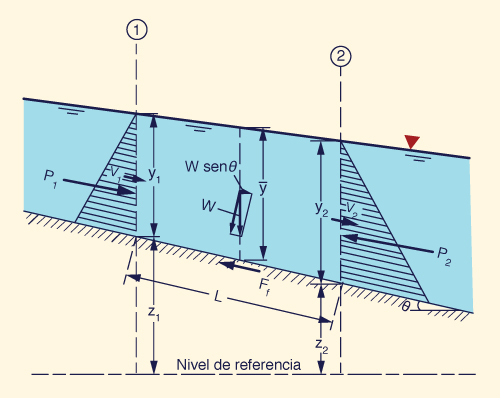
Los embalses, o reservorios, son estructuras naturales o artificiales que producen difusión del escurrimiento. El flujo a través de un embalse está regido por la ecuación diferencial de almacenamiento:
en la cual I = flujo de entrada, O = flujo de salida, y dS/dt = velocidad de cambio del almacenamiento, expresada en unidades L3 T -1 (Fig. 5).
En general, la relación entre el flujo de salida O y el almacenamiento S es:
en la cual K = coeficiente, y m = exponente. Para m = 1, la Ec. 3 se reduce a la forma lineal:
en la cual K = constante de almacenamiento,
con unidades de tiempo (T). En la práctica, la combinación de la Ec. 2 con cualquiera de las Ecs. 3 o 4
produce difusión del escurrimiento.
Una de las funciones de un embalse es difusionar el flujo;
esto le proporciona dos propiedades
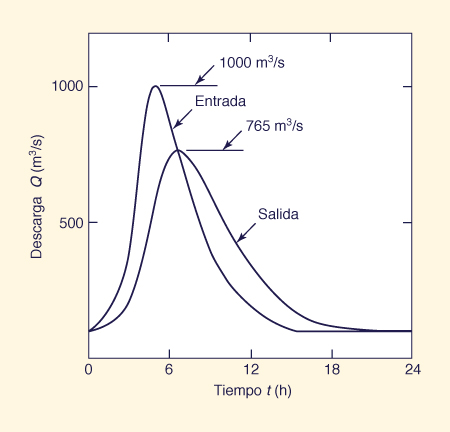
La primera propiedad se debe a que, en un embalse, la superficie del agua es esencialmente horizontal; por lo tanto, la celeridad de las ondas superficiales pequeñas es teóricamente infinita (Ponce, 2014). La segunda propiedad se debe a cuando los flujos de entrada y salida son iguales, el volumen almacenado es el máximo; por lo tanto, el flujo de salida es el máximo (Ec. 4).
2.2.2 Difusión a través de una corriente o canal
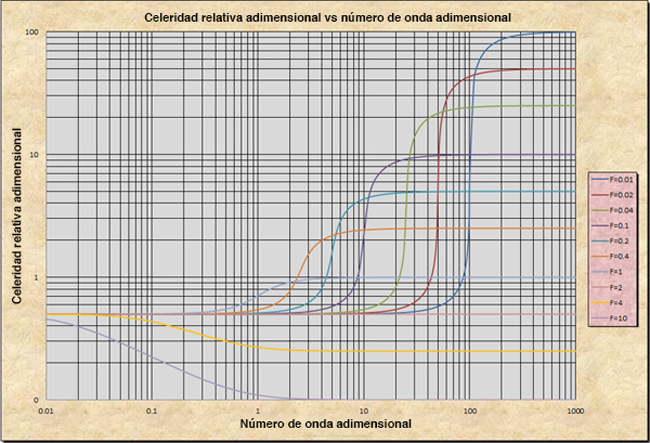
Las corrientes, o canales, son elementos hidráulicos que pueden o no proporcionar difusión del escurrimiento, dependiendo de la escala relativa de la onda de superficie. La magnitud de difusión se caracteriza por el número de onda adimensional σ, como se muestra en la Fig. 7. El número de onda adimensional se define como sigue:
en el cual L = longitud de onda, y Lo = longitud de la corriente (o canal) en el cual el flujo de equilibrio pierde una altura igual a su profundidad (Lighthill and Whitham, 1955):
Existen cuatro tipos de ondas en el flujo en corrientes:
Las ondas cinemáticas se encuentran en el lado izquierdo de la Fig. 7, donde la celeridad relativa adimensional es constante y, por lo tanto, la atenuación es nula. Las ondas dinámicas se encuentran en el lado derecho, también con un valor constante de la celeridad relativa adimensional y, por consiguiente, atenuación nula. Las ondas cinemático-dinámicas mixtas se encuentran hacia el centro de la figura, con celeridad variable y atenuación consecuentemente mayor. Las ondas difusivas son intermedias entre las ondas cinemáticas y las ondas cinemático-dinámicas mixtas, con atenuación pequeña a media. En el drenaje de carreteras, las ondas cinemáticas se aplican en los casos en que la difusión es despreciable o nula; por ejemplo, en el flujo en pendientes fuertes. Las ondas difusivas se aplican cuando la difusión es pequeña; por ejemplo, en pendientes moderadas. Las ondas cinemático-dinámicas mixtas, aplicables usualmente a la rotura de presas, tienen un uso limitado en el drenaje de carreteras. De igual manera, las ondas dinámicas, aplicables a la operación de canales de regadío, tienen un uso limitado en el drenaje de carreteras. Las ecuaciones de continuidad y movimiento del flujo unidimensional no permanente, comúnmente conocidas como las ecuaciones de Saint Venant, pueden ser linearizadas y combinadas en una ecuación de convección-difusión, con la descarga Q como la variable dependiente (Hayami, 1951; Dooge, 1973; Dooge et al., 1982; Ponce, 1991a )
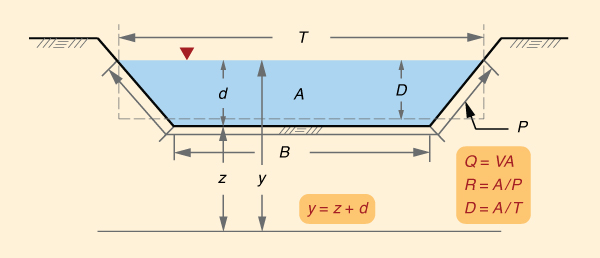
en la cual A = área de flujo;
T = ancho de superficie; So = pendiente del fondo, y
en la cual β = exponente de la curva de gasto (Q = α Aβ), vo = velocidad de flujo, do = profundidad de flujo, y g = aceleración de la gravedad. Nótese que en la Ec. 7, para V = 0, el coeficiente del término de segundo orden se reduce a la difusividad hidráulica cinemática, originalmente debida a Hayami (1951). Por otro lado, para V = 1, el coeficiente se reduce a cero y la difusión desaparece. Bajo esta última condición, todas las ondas, cinemáticas, dinámicas, y mixtas, independientemente de la escala, se propagan a la misma celeridad, fomentando así el desarrollo de ondas de rollo (Fig. 8). Esta condición de estabilidad neutral del flujo (V = 1) debe tomarse en cuenta en el diseño de obras de drenaje urbano y de carreteras.
2.2.3 Difusión a través de una cuenca Una cuenca hidrográfica es una parte de la corteza terrestre que tiene la propiedad de concentrar el escurrimiento superficial en un solo punto, localizado aguas abajo, denominado la boca, o sección de salida, de la cuenca. La Fig. 9 muestra un diagrama de la cuenca del río Alto Parramatta, en Nuevo Gales del Sur, Australia.
La cuenca hidrográfica se describe por sus características geométricas, topográficas, e hidráulicas. Las principales son:
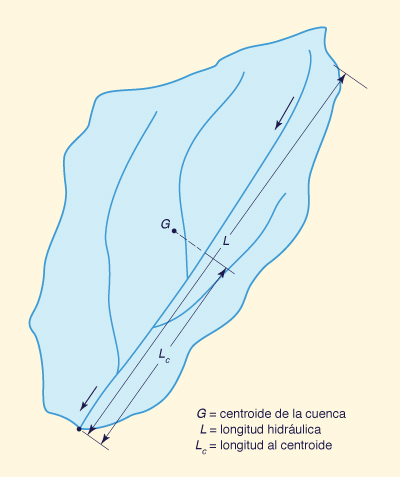
La longitud hidráulica es aquélla medida a lo largo del curso de agua principal (Fig. 10).
El tiempo de concentración es el tiempo que toma un volumen determinado de agua para recorrer la longitud hidráulica y concentrar el flujo en la salida de la cuenca. Bajo condiciones de flujo turbulento, el tiempo de concentración está directamente relacionado con la longitud hidráulica L y la rugosidad de fondo n (es decir, el coeficiente de Manning), e inversamente con la intensidad efectiva de precipitación Ie y la pendiente de fondo So (Ponce, 2014):
en la cual m = exponente de la curva de gasto unitario [en el plano de escurrimiento]
q = ahm,
El escurrimiento superficial en una cuenca puede ser de tres tipos (Ponce, 2014):
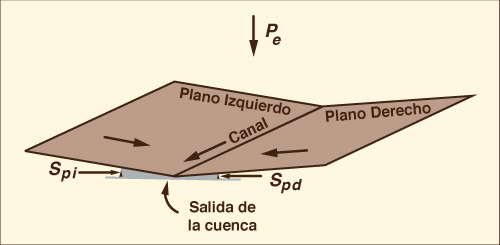
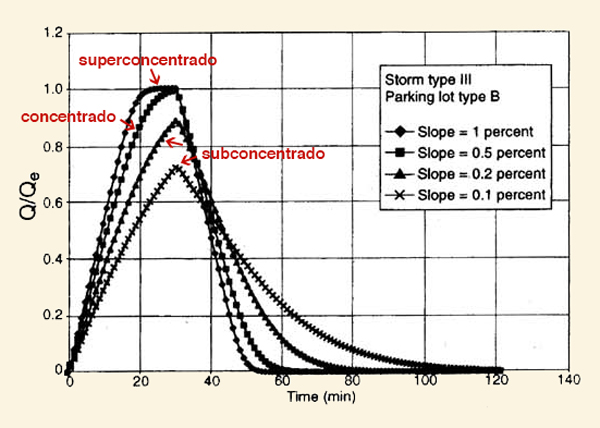
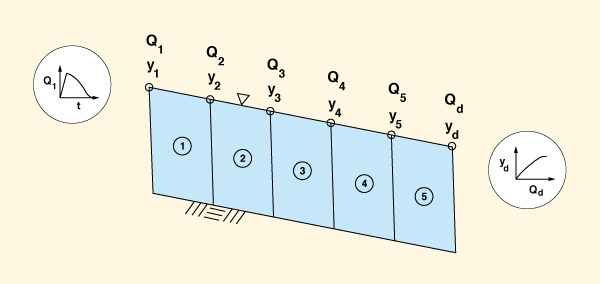
La Figura 11 muestra un esquema de libro abierto utilizado en la modelación del escurrimiento superficial en cuencas. La entrada es la precipitación efectiva en dos planos adyacentes a un canal; la salida es el hidrograma en la boca, o salida, de la cuenca.
La Figura 12 muestra los hidrogramas de salida para los tres casos descritos anteriormente (Ponce y Klabunde, 1999). El caudal máximo posible es: Qp = IeA, en la que Ie = intensidad efectiva de precipitación, y A = área de la cuenca. Por definición, el caudal máximo posible se alcanza en un flujo concentrado o superconcentrado. En el caso del flujo subconcentrado, el caudal no llega a alcanzar el valor máximo posible. Esto representa difusión del escurrimiento, debido a que efectivamente el flujo se ha extendido en el tiempo (y en el espacio).
Por lo tanto, la difusión del escurrimiento en cuencas se produce para todas las ondas o perturbaciones cuando el flujo es subconcentrado, es decir, cuando el tiempo de concentración es mayor que la duración efectiva de precipitación. Esto suele ser así en el caso de las cuencas medianas y grandes, para las cuales la pendiente media de la cuenca (a lo largo de la longitud hidráulica) es suficientemente pequeña.
2.3 Escala de cuencas
El concepto de escala de cuenca y su aplicación al cálculo de la hidrología
de avenidas
es relativamente reciente (Ponce, 1989; 2014). Lo que sí está establecido
hace muchos años
es que la difusión tiende a aumentar con el tamaño de la cuenca.
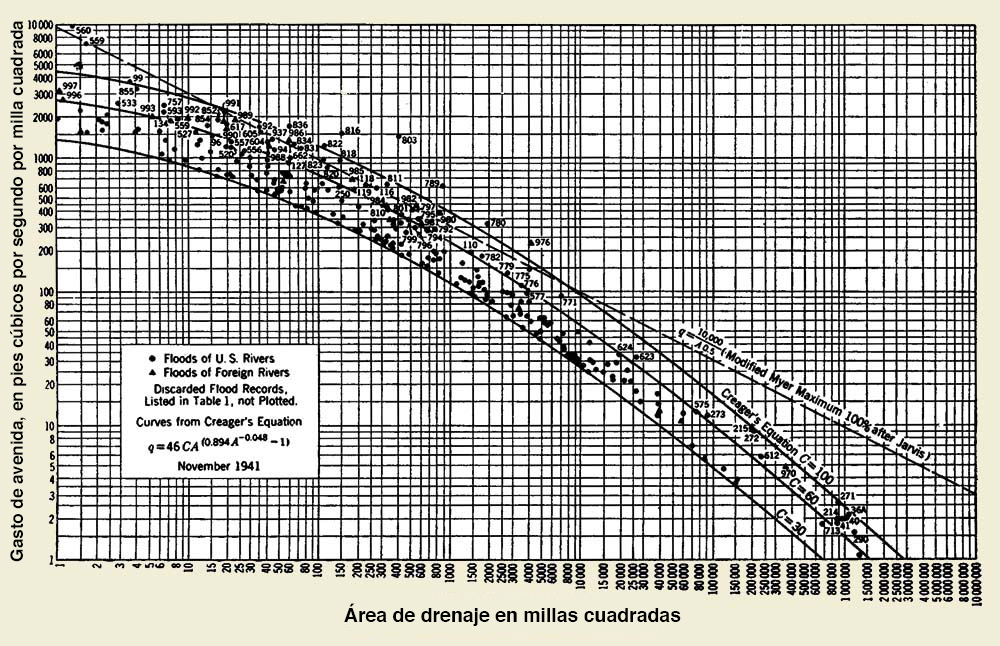
Creager et al. (1945) graficaron por primera vez la descarga de avenida vs el área
de la cuenca
(Fig. 13). El gráfico de Creager muestra claramente que la descarga unitaria
de avenida (la descarga pico por unidad de área) es inversamente proporcional al área
de la cuenca. El gráfico de Creager es empírico,
sin ninguna connotación de frecuencia,
por lo que ha caído en desuso a través de los años. Sin embargo, su mensajes es claro:
En la práctica, la escala de cuenca a analizar varía grandemente. Las cuencas pueden tener desde menos de una hectárea (0.01 km2) (por ejemplo, un desarrollo urbano muy pequeño) hasta varios millones de kilómetros cuadrados (la cuenca del río Amazonas). Los tamaños de cuenca más usuales están en el rango 0.1 km2 a 10 000 km2. Ponce (1989) ha dividido las cuencas, para propósitos de cálculo, en:
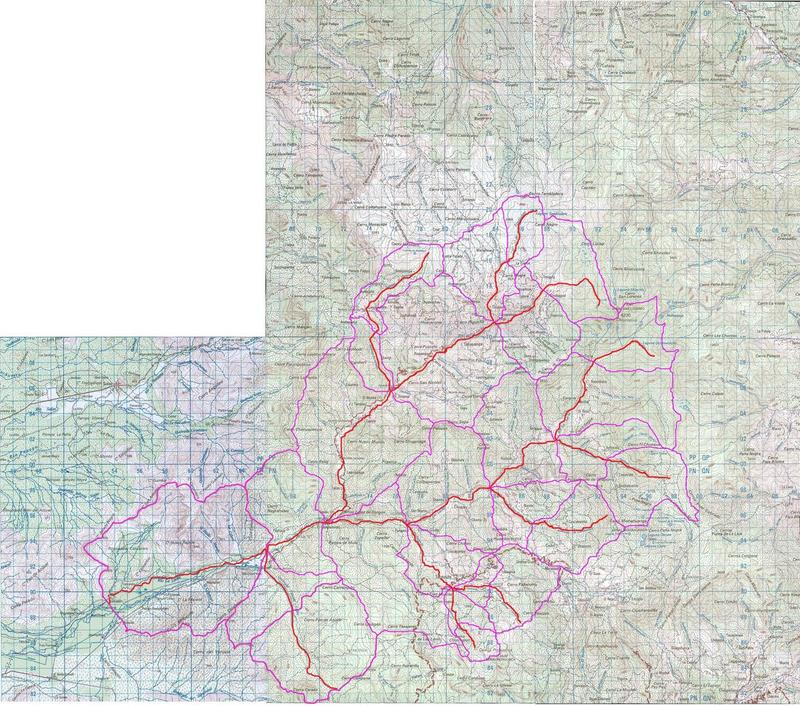
Nótese que la difusión está ausente en las cuencas pequeñas y presente en las cuencas medianas. La Figura 14 muestra la delimitación de la cuenca del río La Leche, en Lambayeque, Perú, aguas arriba de La Calzada (sitio de presa propuesto), la cual drena un área de 907 km2. La red de drenaje está trazada en color rojo, y las divisorias de cuencas en color morado [veintiséis (26) subcuencas].
Todas las obras viales requieren drenaje. El análisis se concentra en la intersección de la red vial con la red natural de drenaje superficial (quebradas, arroyos, corrientes, y ríos). El método de cálculo para determinar la descarga de diseño dependerá del tamaño de la cuenca tributaria. Asimismo, la importancia y el costo de la obra de drenaje dependerán del tamaño de la cuenca.
2.3.1 Relaciones de frecuencia En las cuencas pequeñas, se aplican las curvas de intensidad-duración-frecuencia, a las cuales se las refiere comúnmente por las siglas IDF. Éstas son una serie de curvas de intensidad de precipitación en las ordenadas versus duración en las abscisas, con la frecuencia como el parámetro de las curvas. La frecuencia es el número de años que demora un evento en repetirse; por ejemplo, una vez en 50 años: 1/50, ó 0.02. Las curvas IDF son función del clima prevaleciente y son generadas en forma local o regional.
Las curvas IDF se utilizan en el método racional [Sección 2.4]
para determinar la intensidad, dadas la duración
(la que se asume igual al tiempo de concentración) y la frecuencia.
En las cuencas medianas, se aplican los mapas de profundidad-duración-frecuencia, referidos por las siglas PDF (o, alternativamente,
DDF, su equivalente en Inglés).
Éstos son una serie de mapas de precipitación (P), cada uno aplicable a una duración (D) y frecuencia (F) determinadas.
Los mapas son función del clima prevaleciente, a ser generados en forma local o regional.
Estos mapas Es importante notar que, en cuencas pequeñas, la intensidad de precipitación I (cm/h) es el parámetro de importancia, mientras que en cuencas medianas, lo es la profundidad P (cm).
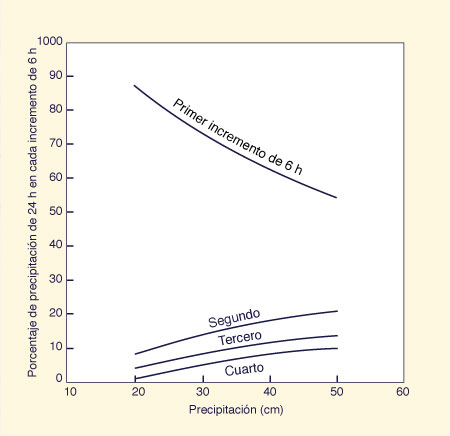
2.3.2 Relaciones temporales En el análisis de cuencas medianas y grandes, es necesario distribuir la tormenta P en la duración D con el fin de obtener un hietograma de tormenta. Para las cuencas medianas, la duración típica es de 6 a 12 h; para las cuencas grandes, es de 24 a 48 h. La Figura 15 muestra un ejemplo de la división de una tormenta estándar de 24 h en cuatro incrementos, o intervalos, de 6 h cada uno (Ponce, 1989).
2.4 El método racional El método racional es el más usado para el análisis de escurrimiento directo en cuencas pequeñas. El método está basado en el principio de concentración del escurrimiento, que establece que la descarga máxima, o descarga pico Qp, es igual al producto de la intensidad de precipitación efectiva Ie por el área de la cuenca tributaria A:
Esto implica que el método racional no considera la difusión, lo cual limita su aplicabilidad a cuencas pequeñas. En la práctica, la intensidad efectiva se estima como una fracción apropiada de la intensidad de precipitación total I:
en la cual C = coeficiente de escurrimiento [del evento], a ser determinado en base a experiencia local o regional. Reemplazando la Ec. 11 en la Ec. 10, la fórmula de método racional es:
En el sistema de unidades SI, la fórmula de método racional es:
en la cual Qp es en L/s, I en mm/h, y A en ha. El valor de C varía teóricamente
en el rango 0-1, aunque los valores más usuales se
encuentran típicamente en el rango 0.3 < C ≤ 0.7. La Tabla 1 muestra coeficientes de escurrimiento
aplicables a zonas rurales.
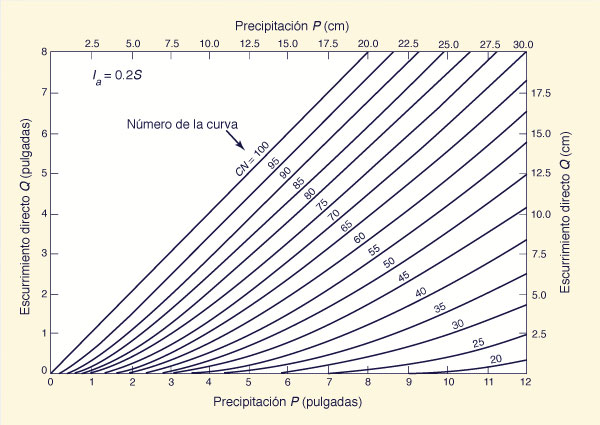
2.5 Abstracciones hidrológicas El método del número de curva fue presentado en 1954 por el Servicio de Conservación de Recursos Naturales de los EE.UU. El método es usado a nivel mundial para calcular la tormenta efectiva, una vez conocidas la tormenta total y un parámetro de abstracción hidrológica denominado "número de la curva," o CN (Curve Number en Inglés). El método fue desarrollado originalmente para ser usado en la abstracción de eventos, aplicable al flujo directo (Sección 2.1) y, por consiguiente, al cálculo de avenidas para las cuales el flujo directo es preponderante. Su uso inicial fue en la hidrología agrícola; posteriormente, su uso fue extendido a las hidrologías forestal, de pastizales, y urbana, y en los últimos años, a otros tipos de hidrología, a falta de métodos alternativos. El método asume la siguiente proporcionalidad entre la retención y el escurrimiento:
en la cual Q = escurrimiento real; P = escurrimiento potencial, es decir, la precipitación; (P - Q) = retención real; y S = retención potencial. El concepto del número de la curva difiere diametralmente del clásico principio de Horton, en el cual el escurrimiento Q es igual a la diferencia entre la precipitación P y la infiltración I (retención); es decir, a mayor retención, menor escurrimiento (Horton, 1933). Contrariamente a esto, en el método del número de la curva, a mayor retención, mayor escurrimiento.
Esta aparente dicotomía se explica de la siguiente manera:
El principio de Horton
asume que el suelo tiene una profundidad infinita, la cual no forma parte del cálculo;
de manera opuesta, en el método del número de la curva,
el suelo tiene una profundidad finita, representada por la retención potencial (el parámetro S).
El método del número de la curva es de naturaleza conceptual; sin embargo, La Ecuación 14 no considera la posibilidad de una abstracción inicial, es decir, de que el escurrimiento Q comience, no para P > 0, sino para P > Pa, en la cual Pa es un valor pequeño, finito. Esta situación se ha resuelto restándole a P una abstracción inicial Ia, compuesta principalmente por intercepción, almacenamiento en la superficie, y alguna infiltración que pueda tener lugar antes de que comience el escurrimiento. Incluyendo la abstracción inicial, la Ec. 14 se expresa como sigue:
Resolviendo para Q:
la cual está sujeta a la siguiente restricción: Q = 0 para P < Ia. La Ecuación 16 tiene dos parámetros: Ia y S. Para simplificar el método, se ha relacionado la abstracción inicial con la retención potencial de la siguiente manera:
Esta relación fue obtenida
en base a datos de precipitación-escurrimiento
en cuencas pequeñas experimentales. El coeficiente 0.2
ha sido objeto de amplio escrutinio.
Por ejemplo, Springer et al. (1980)
evaluaron pequeñas cuencas húmedas y semiáridas y encontraron
que el coeficiente de la Dada la Ec. 17, la Ec. 16 se reduce a:
la cual está sujeta a la siguiente restricción: Q = 0 para P < 0.2 S. La retención potencial S varía dentro de un amplio rango (0 ≤ S ≤ ∞). Para simplificar, se la ha expresado en términos de un parámetro denominado número de la curva, un número entero que varía en el rango de 1 a 100. La ecuación elegida es (Ponce, 1996):
en la cual CN = número de la curva (adimensional) y S,
1000 y 10 son expresados en pulgadas.
Por ejemplo, para CN = 100, S = 0 pulgadas;
y para CN = 1, S = 990 pulgadas.
Por lo tanto, la capacidad para abstracción de precipitación
es inversamente proporcional al número de la curva.
Para Reemplazando la Ec. 19 en la Ec. 18:
la cual está sujeta a la siguiente restricción: Q = 0 para P < [ (200/CN) - 2]. En la Ec. 20, los valores de P y Q están expresados en pulgadas. En unidades SI, la Ec. 20 se convierte a:
la cual está sujeta a la siguiente
restricción: Q = 0 para P <
R [(200/CN) - 2].
Con La Figura 16 muestra un gráfico de la Ec. 20 (pulgadas) y Ec. 21 (centímetros). Cabe notar que el escurrimiento [directo] Q está graficado en función de la precipitación [total] P y del número de la curva CN.
2.6 El hidrograma unitario El método del hidrograma unitario es el más usado para el análisis del escurrimiento superficial en cuencas medianas. El método fue desarrollado como una alternativa para el método racional, aplicable al caso de cuencas medianas, en las cuales la difusión es apreciable (Sherman, 1932).
Cabe anotar que el método del hidrograma unitario se aplica a una cuenca determinada, utiliza sólo una tormenta, y
determina sólo un hidrograma de avenida, a la salida de la cuenca.
Por lo tanto, el método está limitado a cuencas medianas, para las cuales la tormenta
cubre toda la cuenca. Para cuencas grandes, mayores de
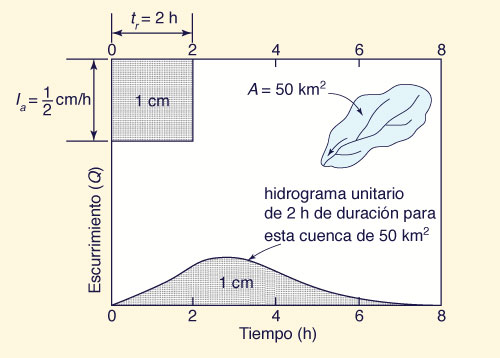
El hidrograma unitario se define como el hidrograma producido
por una unidad de escurrimiento (usualmente
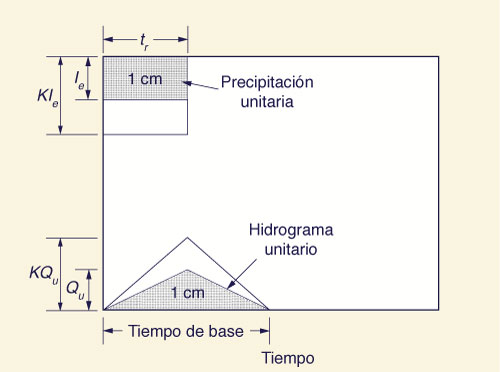
En la Fig. 17, la profundidad de precipitación es 1 cm y
la duración es tr = 2 h; por lo tanto,
la intensidad de precipitación es Ia = 0.5 cm/h.
El hidrograma unitario correspondiente tiene un volumen de 1 cm,
que es igual al volumen escurrido La forma del hidrograma unitario, incluyendo descarga pico y tiempo al pico, describe la difusión de la precipitación efectiva unitaria (1 cm) para una duración dada tr. El hidrograma unitario es el elemento básico en el proceso de convolución (Sección 2.6.5), por medio del cual se calcula el hidrograma de avenida.
2.6.1 Hidrogramas unitarios sintéticos Un hidrograma unitario se puede construir de dos maneras:
El primer método
es poco usado, pues requiere de mediciones de aforos,
que son generalmente escasas. La función de hidrograma unitario sintético es predecir la forma del hidrograma, particularmente la descarga pico Qp y el tiempo pico tp, es decir, el tiempo transcurrido desde el inicio del hidrograma hasta la ocurrencia de la descarga pico. A mayor difusión, menor es la descarga pico y mayor el tiempo transcurrido; contrariamente a esto, a menor difusión, mayor es la descarga pico y menor el tiempo transcurrido. En el límite inferior, cuando la difusión es nula, la descarga pico es la máxima posible y el tiempo transcurrido es igual a la duración de la precipitación unitaria, es decir, a la duración del hidrograma. En resumen:
Nótese que para el caso de ausencia de difusión, la descarga pico del hidrograma unitario sintético es la misma que la del método racional (Sección 2.4). Para el caso de difusión apreciable, es decir, para cuencas medianas, existen dos hidrogramas unitarios sintéticos:
El desarrollo de un hidrograma unitario sintético está basado en el siguiente principio:
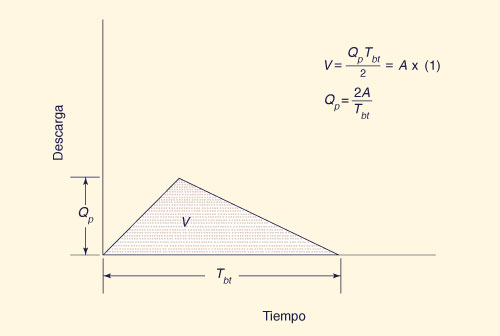
Por ejemplo, si se asume un hidrograma triangular, el volumen es igual a:
en la cual Tbt = tiempo de base del hidrograma unitario triangular (Fig. 18). Por lo tanto, la descarga pico es:
Los hidrogramas unitarios sintéticos relacionan el tiempo del base con un parámetro empírico que caracteriza la difusión, denominado tiempo de retardo, definido como el tiempo transcurrido entre una medida de la precipitación y una medida del escurrimiento; por ejemplo, entre el centroide de la precipitación y el pico del escurrimiento. El tiempo de retardo está directamente relacionado con las longitudes de la cuenca (Fig. 10) e inversamente con la pendiente predominante. A mayor tiempo de retardo, mayor la atenuación del hidrograma unitario y, por lo tanto, mayor la difusión generada por la cuenca.
2.6.2 Hidrograma unitario de Snyder
El hidrograma unitario sintético de Snyder tiene las siguientes propiedades:
En resumen, el hidrograma unitario sintético de Snyder tiene dos parámetros:
A mayor valor de Ct y menor valor de Cp, mayor la magnitud de difusión incorporada en el hidrograma de Snyder. Además, la relación Ct /Cp es directamente proporcional a la magnitud de difusión. Los valores de Ct y Cp se determinan mediante análisis regional, o en base a experiencia local. Las Ecuaciones 24 a 28 pueden utilizarse para estimar la forma del hidrograma unitario de Snyder, teniendo cuenta que el volumen subtendido debe corresponder a 1 cm de escurrimiento.
2.6.3 Hidrograma unitario NRCS A diferencia del hidrograma de Snyder, el cual tiene dos parámetros por determinar, el hidrograma unitario sintético NRCS tiene un solo parámetro, el cual es fijo. Esto resulta en un método simple, pero inflexible. A pesar de esto, el método se mantiene popular, habiendo sido aplicado en los últimos 60 años a nivel global.
El hidrograma unitario NRCS difiere del de Snyder en que usa un valor constante de la relación tiempo-de-base triangular a tiempo
al pico
Para calcular el tiempo de retardo, el método de NRCS utiliza los siguientes procedimientos alternativos:
El método del número de la curva se limita a áreas de menos de 8 km2, aunque la evidencia sugiere que puede extenderse hasta 16 km2 (McCuen et al., 1984). El tiempo de retardo se expresa mediante la siguiente fórmula:
en la cual tl = tiempo de retardo, en horas; L = longitud hidráulica, en m (Fig. 10); CN = número de la curva (Sección 2.5); y Y = pendiente media, en m/m.
Alternativamente, el método de la velocidad se utiliza para cuencas mayores de 8 km2,
o para cuencas con números de la curva fuera del rango
En el hidrograma unitario NRCS, la relación de tiempo al pico tp a duración tr es fija:
Por definición, el tiempo al pico es:
Eliminando tr de las Ecs. 31 y 32:
Por lo tanto:
y, combinando las Ecs. 30 y 34, sólo para el caso del método de la velocidad:
Reemplazando Tbt /tp = 8/3 en la Ec. 23:
En el sistema de unidades SI, la descarga pico es:
en la que Qp = descarga pico del hidrograma unitario NRCS, en m3/s; A = área de la cuenca, en km2; y tp = tiempo al pico, en horas.
Teniendo en cuenta las Ecs. 30 y 32, el tiempo al pico se puede calcular
de la siguiente manera:
2.6.4 Cambio de duración del hidrograma unitario
Toda cuenca tiene varios hidrogramas unitarios, correspondientes a varias duraciones posibles
(usualmente 1 h, 2 h, 3 h, 6 h,
12 h, y El Ejemplo No. 5 detalla el cálculo del método de superposición para calcular los hidrograma unitarios de 2 h y 3 h, dado el hidrograma de 1 h. El Ejemplo No. 6 detalla el cálculo del método del hidrograma S para calcular los hidrograma unitarios de 3 h y de 1 h, dado el hidrograma de 2 h.
2.6.5 Convolución
Mediante la convolución, el hidrograma unitario se usa junto con
la tormenta efectiva para calcular el hidrograma de avenida, es decir, el hidrograma
aplicable para el diseño del drenaje de carreteras en cuencas medianas.
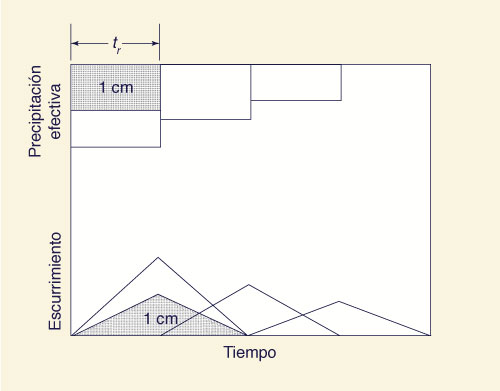
La convolución tiene tres componentes: (a) linearidad, Linearidad. Dado un hidrograma unitario (profundidad = 1 cm), se puede obtener un hidrograma para una profundidad K multiplicando las ordenadas del hidrograma unitario por K, como se muestra en la Fig. 20 (a). El tiempo de base se asume constante e independiente de la profundidad.
Retardo. El tiempo de base constante de todos los hidrogramas obtenidos mediante linearidad es igual al del hidrograma unitario. Por lo tanto, dado un hietograma de tormenta efectiva, se puede calcular un hidrograma parcial para cada incremento de tormenta, cada uno retrasado un intervalo del anterior, como se muestra en la Fig. 20 (b).
Superposición. La suma de las ordenadas correspondientes de estos hidrogramas parciales produce el hidrograma compuesto, como se muestra en la Fig. 20 (c).
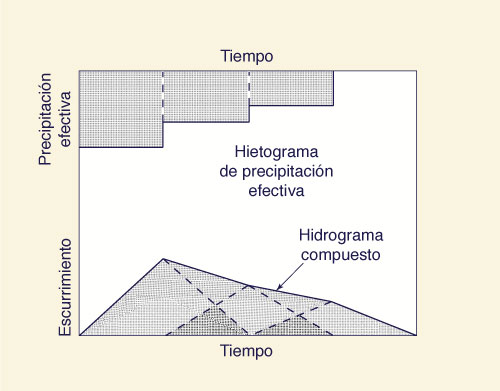
El procedimiento completo [Figs. 20 (a), (b) y (c)]
se conoce como la convolución
del hidrograma unitario con el hietograma de tormenta efectiva, y el resultado es el hidrograma
compuesto.
Ejemplo No. 7.
El siguiente hidrograma unitario de 1-h se aplica
a una cuenca de 10 km2:
Una tormenta de 6-h de duración,
con un total de 5 cm de precipitación efectiva, cubre toda la cuenca
y tiene la siguiente distribución:
Calcular el hidrograma compuesto utilizando convolución.
Solución.
Los cálculos se muestran en la Tabla 6. La Col. 1 muestra el tiempo en horas.
La Col. 2 muestra las ordenadas del hidrograma unitario.
La Col. 3 muestra el producto de la
precipitación de la primera hora (0.1 cm)
por las ordenadas del hidrograma unitario.
La Col. 4 muestra el producto de
la precipitación de la segunda hora (0.8 cm)
por las ordenadas del hidrograma unitario,
con un retraso de 1 h con respecto a la Col. 3.
El patrón de cálculo establecido por las
Cols. 3 y 4 se repite para las Cols. 5 a 8.
La Columna 9, la suma de las Cols. 3 a 8, es el hidrograma compuesto
calculado para el hidrograma unitario (Col. 2) e
hietograma de tormenta efectiva dados.
La suma de la Col. 2 es 280 m3/s y es equivalente a 1 cm de precipitación efectiva.
La suma de la Col. 9 es
CÁLCULO EN LÍNEA. Usando el calculador
ONLINE
CONVOLUTION, con CN = 100,
pues el hietograma dado es de
precipitación efectiva, el hidrograma compuesto calculado es el mismo
de aquél mostrado en la Col. 9
de la Tabla 6.
2.6.6 Resumen
Los siguientes pasos son necesarios para determinar el hidrograma de avenidas
de una cuenca mediana:
Determinación
de la intensidad y duración de la tormenta de diseño en el caso de
cuencas pequeñas; o, alternativamente, la profundidad y duración en el caso de
cuencas medianas [Sección 2.3.1].
Determinación del hietograma
de la tormenta de diseño, en intervalos de Y horas Estimación del número de la curva CN
aplicable a las condiciones hidrológicas de la cuenca
[Sección 2.5; Ejemplo No. 2].
Utilizando el
número de la curva CN, determinación del hietograma
de la tormenta efectiva [Sección 2.5; Cálculo del hidrograma unitario
de X horas de duración
aplicable para la cuenca dada [Sección 2.6.2 ó 2.6.3; Ejemplo No. 4].
Confirmación
de que X = Y.
De no ser así, cambiar la duración inicial del hidrograma unitario,
de tal manera que la duración final del hidrograma unitario
sea igual a Y horas
[Sección 2.6.4; Ejemplo No. 5 ó 6].
Convolución del
hidrograma unitario con el hietograma de la tormenta efectiva para calcular
el hidrograma compuesto, es decir, el hidrograma de la
avenida de diseño
2.7 Métodos estadísticos
Los métodos estadísticos se utilizan en el análisis de cuencas medianas
y grandes, cuando existen datos de descarga medidos en una estación de aforos.
La precisión de los resultados depende de la longitud de la serie de descargas máximas.
Por ejemplo, para asegurar la confiabilidad de una avenida de 50 años de período de retorno,
calculada con métodos estadísticos, se requiere que
la longitud del registro sea de por lo menos de 25
a 50 años.
Cabe anotar que debido al cambio climático, la confiabilidad
del análisis estadístico se ha visto
reducida en los últimos años en forma considerable.
Por lo tanto, esta realidad debe ser tomada
en cuenta en el análisis.
La frecuencia de avenidas se refiere al uso de análisis de frecuencia para el cálculo
de avenidas de diseño. A través del último siglo, se han desarrollado varias
distribuciones estadísticas para el análisis de frecuencia
(Ponce, 2014).
En la práctica, los métodos más usados son
los métodos de Gumbel y
2.7.1 Selección de la serie de descargas máximas
El registro completo de los caudales en una estación de aforo
se denomina la serie completa. Para el
análisis de frecuencia de avenidas, es necesario seleccionar una
serie de avenidas, es decir, una muestra de los eventos de
avenidas extraídos de la serie completa.
Existen dos tipos de series de avenidas: (1) la serie de duración parcial, y (2)
la serie de valores extremos. La serie de duración parcial
consta de avenidas cuya magnitud es mayor que un valor base
elegido. Cuando el valor base es tal que el número de eventos de la
serie es igual al número de años de registro, la serie se denomina
serie de excedencia anual.
En la serie de valores extremos, cada año de registro contribuye con un
valor a la serie, ya sea el valor máximo (en el
caso del análisis de avenidas), o el valor mínimo (en el
caso del análisis de la permanencia de flujos bajos). El primero es la serie
máxima anual; el segundo es la serie mínima anual.
La serie de excedencia anual tiene en cuenta todos los eventos extremos
por encima de un cierto valor base, independientemente del momento en que
ocurrieron. Por el contrario, la serie máxima anual considera sólo un evento
extremo por cada año de registro. La diferencia entre estas
dos series es más marcada para los registros cortos, en los que los segundos
eventos anuales mayores pueden influir fuertemente en el carácter de la
serie de excedencia anual. En la práctica, la serie de excedencia anual
se usa para el análisis de frecuencia con períodos de retorno
cortos, de 2 a 10 años. Para períodos de retorno más largos, la
diferencia entre las series de excedencia anual y máxima anual es pequeña. La
serie máxima anual se utiliza para períodos de retorno mayores de
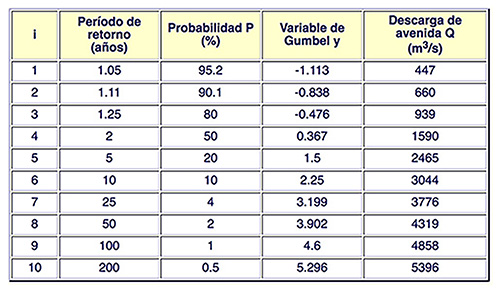
2.7.2 Método de Gumbel
La distribución de valor extremo Tipo I, conocido como
el método de Gumbel, ha sido ampliamente utilizado a nivel global
La probabilidad acumulativa del método de Gumbel es:
en la cual F(x) = probabilidad de no excedencia, e y = variable de
Gumbel.
En el análisis de frecuencia de avenidas, la probabilidad de interés es la probabilidad de excedencia, es decir, la probabilidad complementaria a F(x):
El período de retorno T es el
recíproco de la probabilidad de excedencia
[T = G -1 = P -1].
Por lo tanto:
Resolviendo para y:
La fórmula de frecuencia es:
en la cual x = variable de análisis; x̄ = media de x;
s = desviación estándar de x; y K = factor de frecuencia.
Este último se evalúa aplicando la
fórmula de frecuencia a la variable de Gumbel (y):
en la cual ȳn y σn
son la media y la desviación estándar de la variable
de Gumbel, respectivamente (ver
Tabla A-1).
Reemplazando la Ec. 43 en la Ec. 42:
Reemplazando la Ec. 41 en la Ec. 44:
La aplicación del método de Gumbel consiste de los siguientes pasos:
Selección de la serie de avenidas, con longitud de registro n.
Cálculo de la media x̄ y la desviación estándar
s de la serie de avenidas.
Determinación de la media ȳn
y la desviación estándar σn
de la variable de Gumbel utilizando la Tabla A-1.
Selección de varios períodos de retorno Tj y sus correspondientes probabilidades de
excedencia Pj.
Cálculo de
la descarga de avenida Qj
para cada período de retorno Tj
utilizando la
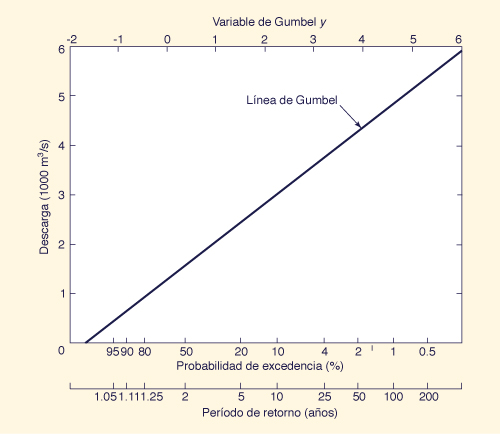
Los valores de Q vs T (o P) se grafican
en un papel de probabilidad de Gumbel
y se traza una línea recta a través de los puntos.
El papel de probabilidad de Gumbel
muestra la variable de
Gumbel (y) en las abscisas y
la descarga de avenida (Q)
en las ordenadas.
Ejemplo No. 8.
Aplicar el método de Gumbel a la siguiente serie
de descargas máximas anuales, con n = 16:
Solución. La media y la desviación estándar son, respectivamente:
x̄ = 1704 m3/s y s =
La Tabla 7 resume los resultados.
Las Cols. 1 y 2 muestran, respectivamente, los períodos de retorno seleccionados y sus
correspondientes probabilidades de excedencia.
La Col. 3 muestra los valores de la variable de Gumbel calculados utilizando la Ec. 41.
La Col. 4 muestra las descargas de avenida calculadas utilizando la
Fig. 21
Análisis de frecuencia de avenidas por el método de Gumbel.
CÁLCULO EN LÍNEA.
Utilizando EN LÍNEA GUMBEL,
se obtienen los resultados mostrados en la tabla que sigue, confirmándose
que son prácticamente los mismos de
la Tabla 7.
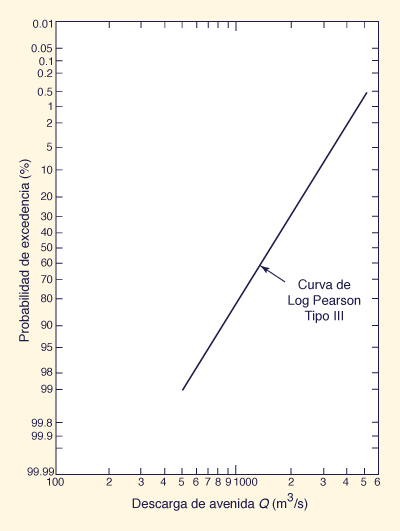
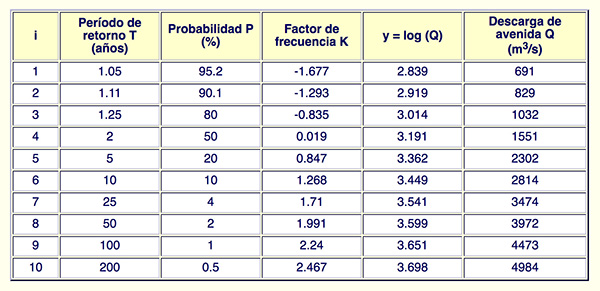
2.7.3 Método de Log Pearson Tipo III
El método de Log Pearson Tipo III
es usado a nivel global
para el análisis de frecuencia de avenidas.
El método ha sido recomendado por el Boletín 17B del Comité Consultivo Intergubernamental
de Registros de Agua de los EE.UU.
La aplicación del método Log Pearson Tipo III consiste de los siguientes pasos:
Selección de la serie de descargas máximas
anuales xi, con período de registro n.
Cálculo de la serie de logaritmos yi :
Cálculo de la media ȳ, desviación estándar sy,
y coeficiente de asimetría
Csy de la serie de logaritmos yi .
Cálculo de los logaritmos de las descargas de avenida log Qj,
para varios niveles de probabilidad seleccionados Pj, utilizando
la fórmula de frecuencia:
En esta ecuación (Ec. 47), el factor de frecuencia Kj es función de la probabilidad
Pj y el coeficiente de asimetría Csy (Tabla A-2).
Cálculo de la descargas de avenida Qj para cada nivel de probabilidad
Pj (o período de retorno Tj correspondiente)
tomando los antilogaritmos:
Representación gráfica de las descargas de avenida Qj versus las probabilidades
Pj en papel logarítmico de probabilidades,
con las descargas en la escala logarítmica y las probabilidades en
la escala de probabilidades. El resultado del método Log Pearson
La Tabla A-2
muestra los factores de frecuencia
K para diez (10) niveles de probabilidad seleccionados
en el intervalo de 0.5 a 95 por ciento
(con períodos de retorno correspondientes de 200 a 1.05 años)
y coeficientes de asimetría en el rango de -3.0 ≤ Csy ≤ 3.0.
Ejemplo No. 9.
Aplicar el método de Log Pearson Tipo III a la serie de descargas máximas
del Ejemplo No. 8 (método de Gumbel).
Solución. Se toman los logaritmos de la serie de descargas máximas,
y se calculan la media, desviación
estándar y coeficiente de asimetría de la serie de logaritmos:
ȳ = 3.187, sy = 0.207,
y
La Tabla 8 resume los resultados. La Col. 1 muestra
los períodos de retorno seleccionados. La Col. 2 muestra las
probabilidades de excedencia correspondientes en porcentaje.
La Col. 3 muestra los factores de frecuencia
K, para Csy = - 0.116
y para cada período de retorno y probabilidad de excedencia.
Fig. 22 Analisis de frecuencia de avenidas por el método de Log Pearson Tipo III.
CÁLCULO EN LÍNEA.
Utilizando EN LÍNEA PEARSON,
se obtienen los resultados mostrados en la tabla que sigue, confirmándose
que son prácticamente los mismos de
la Tabla 8.
Comparación de métodos. Se observa que los resultados de la aplicación de los métodos
de Gumbel (Tabla 7) y Log Pearson Tipo III
(Tabla 8) a la misma serie de avenidas son comparables, mas no iguales.
Por lo tanto, el analista debe ejercitar su juicio y usar su experiencia para determinar
el valor de descarga más apropiado para el diseño.
2.8 Métodos regionales
El análisis regional comprende el estudio
de fenómenos hidrológicos con el fin de desarrollar relaciones
matemáticas que puedan ser aplicadas en un contexto regional. El objetivo
es permitir que la información existente
en cuencas aforadas o de registro largo pueda ser transferida fácilmente
a cuencas no aforadas o de series de registros cortos, con
características hidrológicas similares.
En el caso de flujos de avenida, el objetivo del análisis regional
es relacionar la descarga pico de una frecuencia dada
con parámetros descriptivos de la cuenca, tales como: (a) área de drenaje,
(b) precipitación media anual, y (c) elevación media de la cuenca.
Siguiendo este procedimiento, el Servicio Geológico de los EE.UU.
(USGS por sus siglas en Inglés)
ha desarrollado
a través de las últimas décadas las llamadas
Ecuaciones de Estados,
las cuales relacionan, para cada estado de la unión,
las descargas pico
con parámetros descriptivos de la cuenca.
Por ejemplo, para California, la Ecuación del Estado USGS es
la siguiente:
QT = a A b P c E d
en la cual QT = descarga pico correspondiente al período de retorno T,
a la salida de la cuenca;
A pesar de su popularidad y uso extensivo, la confiabilidad de las Ecuaciones de Estado USGS
no está claramente establecida.
Por ejemplo, en el caso de California, la primera versión de las ecuaciones, publicada en el año
1977, ha sido recientemente (2012) reemplazada por un nuevo grupo de ecuaciones, con mayor cantidad de
datos y, por consiguiente, supuestamente de mayor confiabilidad. Sin embargo, la diferencia entre
las dos versiones puede ser marcada; ver Ejemplo
En general, el análisis
regional se recomienda para uso en drenaje
de carreteras para proyectos preliminares, o en los casos en que
la ausencia de datos dificulta una evaluación
más detallada.
Ejemplo No. 10.
Calcular la descarga pico Q100 aplicable a una cuenca en el condado de San Diego,
California, EE.UU., con los siguientes datos: Área de drenaje A = 182 km2,
precipitación media anual P = 22 cm; elevación media
CÁLCULO EN LÍNEA. Usando el calculador
ONLINE USGS FLOODS CALIFORNIA, en la Región 5 (Costa Sur), correspondiente a San Diego,
2.9 Modelación del escurrimiento
En cuencas grandes, a menudo es necesario modelar separadamente todos los componentes
del proceso, incluyendo precipitación, abstracciones hidrológicas, transformación hietograma efectivo-escurrimiento,
y flujo en corrientes, ríos, y
Determinación del área de la cuenca;
Identificación de la red de drenaje;
División de la cuenca en varias subcuencas;
Generación del
hidrograma de avenida a la salida de cada subcuenca;
Tránsito de los
hidrogramas a través de la red de drenaje;
Combinación de los hidrogramas de las subcuencas, en el tiempo
y en el espacio; y
Cálculo del hidrograma de avenida
en el punto de interés.
La modelación comprende los siguientes pasos:
Selección de la
tormenta total [Sección 2.3.1];
Para cada subcuenca, abstracción de la tormenta total con el fin
de
calcular la tormenta efectiva [Sección 2.5];
Para cada subcuenca,
transformación del hietograma efectivo en
el hidrograma de avenidas [Sección 2.6];
Tránsito de los flujos
de avenida en las corrientes, ríos, y embalses;
En el paso No. 3, la transformación hietograma/hidrograma puede hacerse de dos maneras:
Método conjunto: Convolución
del hietograma efectivo con el hidrograma unitario, lo cual genera un solo hidrograma
a la salida de la cuenca (Sección 2.6.5); y
Método distribuido: Modelación con libro abierto (Fig. 11) y ondas cinemáticas
o difusivas, con la cual se puede
generar hidrogramas en varios puntos de la cuenca (Sección 2.2.2).
En el paso No. 4, el tránsito de avenidas a través de
corrientes se puede hacer con uno de varios métodos, entre otros:
Ondas cinemáticas (Sección 2.2.2);
Ondas difusivas (Sección 2.2.2);
Muskingum; y
Muskingum-Cunge.
El método Muskingum calcula el tránsito de avenidas usando
una ecuación empírica que relaciona el almacenamiento S (volumen) del tramo de canal
o río
con dos parámetros: K = tiempo de tránsito, y X = factor de
ponderación (Chow, 1959).
El método Muskingum-Cunge simula la onda difusiva igualando: (a) las celeridades
analíticas y numéricas, y (b) las difusividades
analíticas y numéricas,
de la ecuación de conveccion-difusión de la descarga o caudal de avenida
(Cunge, 1969;
En la práctica, la modelación
del escurrimiento en cuencas se hace con modelos hidrológicos establecidos a
través de los años.
El modelo más utilizado es el
3. HIDRÁULICA
3.1 Flujo en canales abiertos
El flujo en quebradas, corrientes, ríos, y canaletas de drenaje es de superficie libre y,
por lo tanto, está sujeto a la presión atmosférica, denominándose también
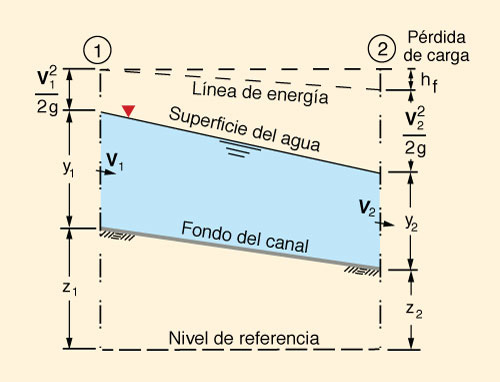
flujo en canales abiertos (Fig. 23).
La profundidad de flujo
medida sobre el fondo del cauce o canal define la elevación
de la superficie del agua. La carga total de
la línea de energía incluye la carga
de velocidad
Existen dos tipos de secciones transversales:
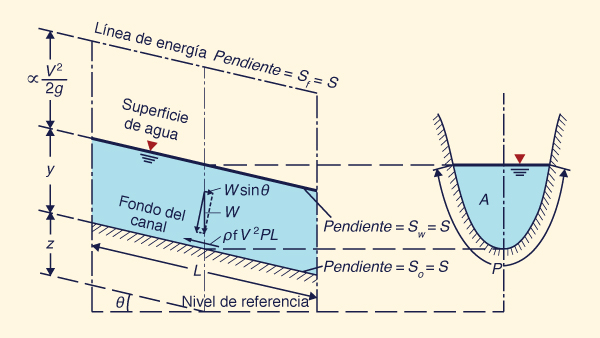
Los canales artificiales son por lo general prismáticos, de forma y tamaño constantes a lo largo de gran parte de la longitud del canal. Por el contrario, generalmente los canales naturales son no prismáticos, es decir, la forma y tamaño de la sección transversal varían a lo largo del canal. Las siguientes propiedades geométricas e hidráulicas describen un canal o cauce (Fig. 25):
En las secciones prismáticas, el tirante d generalmente se describe como y, particularmente cuando no se puede confundir con la elevación de la superficie libre (sobre el nivel de referencia). Además, el talud del canal se describe como z H: 1 V, particularmente cuando no se puede confundir con la elevación del fondo del canal. El flujo en canales abiertos se puede clasificar como sigue:
El flujo es uniforme cuando el canal es prismático y las variables hidráulicas (Q, A, V, d, etc.) son constantes en el tiempo y en el espacio. El flujo está en equilibrio cuando el canal no es prismático y las variables hidráulicas son aproximadamente constantes en el tiempo y el espacio. El cálculo del flujo uniforme es relativamente sencillo en comparación con el de otros estados de flujo. El flujo es gradualmente variado cuando la descarga Q es constante pero las otras variables hidráulicas (A, V, d, etc.) varían gradualmente en el espacio. En el flujo gradualmente variado, la distribución de presiones en la dirección vertical, normal al flujo, es aproximadamente igual a la hidrostática, es decir, es proporcional a la profundidad de flujo. El flujo es rápidamente variado cuando la descarga es constante pero las otras variables hidráulicas (A, V, d, etc.) varían rápidamente en el espacio. Por lo tanto, no es posible asumir que la presión es hidrostática en la dirección vertical. El cálculo del flujo gradualmente variado es complicado pero factible, mientras que el cálculo del flujo rápidamente variado es generalmente más complejo, y está basado en fórmulas empíricas, en ausencia de una solución teórica. El flujo es permanente cuando las variables hidráulicas (flujo, área de flujo, velocidad media, profundidad del flujo, etc.) no varían con el tiempo. Por el contrario, el flujo es no permanente cuando las variables hidráulicas varían con el tiempo y el espacio. El flujo permanente es relativamente más sencillo de calcular que el flujo no permanente. El flujo es espacialmente variado cuando la descarga Q varía en el espacio solamente, es decir, a lo largo del canal. Generalmente, dicha variación se debe a la entrada o salida lateral de flujo. El flujo permanente gradualmente variado comprende los perfiles de la superficie del agua, a los cuales se les conoce como curvas de remanso. El flujo no permanente gradualmente variado está representado por los flujos de inundación, o tránsito de avenidas. El flujo permanente rápidamente variado comprende el flujo sobre vertederos y el resalto hidráulico. El flujo no permanente rápidamente variado está representado por el resalto hidráulico en movimiento y las ondas de rollo en canales de pendiente alta.
3.2 Estado de flujo
El estado de flujo puede ser descrito en base a ciertas velocidades y viscosidades características.
Dos relaciones de velocidad y dos de difusividad completan la caracterización del flujo en canales. Las relaciones de velocidad dan lugar a los números de Froude y Vedernikov; las relaciones de difusividad dan lugar a los números de Reynolds y de onda adimensional. 3.2.1 Relaciones de velocidad Existen tres velocidades características en el flujo en canales:
La velocidad media del flujo uniforme se define con la ecuación de Manning (unidades SI):
en la cual n = coeficiente de fricción de Manning, R = radio hidráulico, y S = pendiente de fricción. Alternativamente, con la ecuación de Chezy, la velocidad media es:
en la cual C = coeficiente de Chezy.
El volumen de control del flujo en canales está sujeto a la acción de cuatro fuerzas: (1) fricción,
La celeridad de la onda cinemática, o celeridad de Seddon,
es (Seddon, 1900;
en la cual β = exponente de la relación entre descarga y área de flujo:
Las ondas dinámicas son aquéllas para las cuales el balance de la cantidad de movimiento se define solamente en base a las fuerzas de inercia y el gradiente de presiones. La celeridad de la onda dinámica es:
en la cual g = aceleración de la gravedad, y D = profundidad hidráulica, D = A /T. De la Ec. 52, la celeridad relativa de la onda cinemática es:
De la Ec. 54, el valor absoluto de la celeridad relativa de la onda dinámica es:
En canales rectangulares, para los cuales D = d, o en canales hidráulicamente anchos, para los cuales D ≅ d, y d = y para canales prismáticos, la celeridad relativa de la onda dinámica es:
La Ec. 57 es la celeridad relativa de Lagrange, en honor a Lagrange (1788), quien fue el primero en derivarla. Las tres velocidades u, v, y w conducen a dos relaciones independientes de velocidad, los números de Froude y Vedernikov. El número de Froude se define como sigue (Chow, 1959):
El número de Froude clasifica al flujo en:
En el flujo subcrítico, las ondas superficiales (perturbaciones) pueden trasladarse aguas arriba, ya que la celeridad -w es mayor que la velocidad media del flujo u. En el flujo crítico, las ondas superficiales (perturbaciones) permanecen estacionarias, ya que su celeridad (absoluta) w es igual a la velocidad media del flujo u. En el flujo supercrítico, las ondas de superficiales (perturbaciones) pueden trasladarse únicamente aguas abajo, debido a que su celeridad -w es menor que la velocidad media del flujo u.
El número de Vedernikov se define como sigue (Vedernikov, 1945; 1946; Powell, 1948; Craya, 1952):
El número de Vedernikov clasifica al flujo en:
En el flujo estable, la celeridad relativa de la onda cinemática v es menor que la celeridad relativa de la onda dinámica w; por lo tanto, las ondas superficiales (perturbaciones) tienen la capacidad de disiparse. En el flujo neutralmente estable, la celeridad relativa de la onda cinemática v es igual a la celeridad relativa de la onda dinámica w; por lo tanto, las ondas superficiales (perturbaciones) no se atenúan ni se amplifican. La amplificación y la disipación se cancelan mutuamente. En el flujo inestable, la celeridad relativa de la onda cinemática v es mayor que la celeridad relativa de la onda dinámica w. Por lo tanto, las ondas superficiales (perturbaciones) tienden a amplificarse. En la práctica, la condición V ≥ 1 conduce al desarrollo de las ondas de rollo, un tren de ondas que se traslada aguas abajo, en canales de pendiente pronunciada (Cornish, 1907) (Fig. 26).
La tercera relación, dependiente de las otras dos, es:
en la cual β - 1 es la celeridad relativa adimensional de la onda cinemática. Por lo tanto, el exponente β de la Ec. 53 es una función de ambos números: el de Froude y el de Vedernikov. El valor de β varía con el régimen de fricción (laminar, transicional, o turbulento, y Manning o Chezy) y con la forma de la sección transversal. En el flujo laminar, β = 3. En el flujo turbulento con la fricción de Manning: 1 ≤ β ≤ 5/3, dependiendo de la forma de la sección transversal. En el flujo turbulento con la fricción de Chezy: 1 ≤ β ≤ 3/2, dependiendo de la forma de la sección transversal. En la hidráulica de canales existen tres tipos asintóticos de secciones transversales:
Para la estabilidad neutral, el número de Vedernikov V = 1. Por lo tanto, de acuerdo con la Ec. 60, el número de Froude correspondiente al flujo neutralmente estable es:
La Tabla 9 muestra los valores de Fns para diversos valores de β.
Se observa que cuando β varía de
3 (flujo laminar) a 1 (sección
inherentemente estable),
los valores de Fns varían de Fns = 1/2 a
En la práctica, el valor de fricción tiene un límite inferior. Por lo tanto, el número de Froude tiene un limite superior, aproximadamente F ≅ 25. Así, en la mayoría de los casos, un valor de β = 1.04 ya sería estable para propósitos prácticos.
La Tabla 9 indica que los valores de β para canales y para flujo laminar están
limitados
en el rango
3.2.2 Relaciones de viscosidad Existen tres clases o tipos de viscosidad en el flujo en canales abiertos:
La viscosidad cinemática ν del fluido varía en función de la temperatura (Tabla A-3). El concepto de difusividad hidráulica νh se debe a Hayami (1951). Hayami combinó las ecuaciones que gobiernan el comportamiento del flujo en canales abiertos, obteniendo una ecuación de convección-difusión, es decir, una ecuación que describe la convección (un proceso de primer orden) y la difusión (un proceso de segundo orden) de una onda de avenida. La difusividad hidráulica se define como sigue:
en la cual qo = descarga de equilibrio, por unidad de ancho, y So = pendiente de fricción (pendiente de la línea de energía). La Ec. 62 se expresa en términos de la velocidad y la profundidad del flujo como sigue:
Una variable relacionada con la difusividad, pero independiente de la pendiente, es:
Por lo general, para cualquier forma de sección transversal:
en la cual Ro = radio hidráulico. En la teoría de la onda cinemática, la longitud característica de tramo se define de la siguiente manera (Lighthill y Whitham, 1955):
en la cual Lo es la longitud del canal en la cual el flujo de equilibrio tiene una pérdida de carga (caída) igual a su profundidad. Por lo tanto, en términos de la longitud característica de tramo, la difusividad hidráulica es:
De manera semejante a la difusividad hidráulica, la difusividad de onda se define de la manera siguiente:
en la cual L = longitud de onda. El número de Reynolds R es (Chow, 1959):
El número de Reynolds R clasifica al flujo en:
Bajo flujo permanente, el flujo laminar
está representado por R ≤ 500 y el flujo turbulento con R > 2000. El flujo de
transición comprende el rango intermedio: En la práctica, la mayoría de los casos de flujo en canales se encuentran sujetos a un régimen turbulento. Por el contrario, la mayoría de los casos de flujo en planos de superficie libre se encuentran bajo régimen laminar o laminar-turbulento mixto. El número de onda adimensional σ se define como sigue (Ponce y Simons, 1977):
El número de onda σ describe la escala adimensional de longitud de onda en términos de: (a) ondas cinemáticas, (b) ondas dinámicas, y (c) ondas cinemáticas-dinámicas mixtas, como se muestra en la Fig. 7, aplicable a la fricción de Chezy en canales hidráulicamente anchos. Bajo el flujo cinemático, el cual se muestra en el lado izquierdo de la Fig. 7:
Bajo el flujo dinámico, el cual se muestra en el lado derecho de la Fig. 7:
Bajo el flujo cinemático-dinámico mixto, el cual se muestra hacia el centro de la Fig. 7:
La difusividad hidráulica dinámica considera el balance completo
de la cantidad de movimiento (Dooge et al., 1982;
Ponce, 1991a; 1991b), a diferencia de la
difusividad hidráulica cinemática (
Para números de Vedernikov bajos, V ⇒ 0, la difusividad hidráulica dinámica se reduce a la difusividad hidráulica cinemática, es decir, a la Ec. 62. Por el contrario, para número de Vedernikov altos, V ⇒ 1, la difusividad hidráulica desaparece por completo. La ausencia total de atenuación es una condición necesaria para la formación de las ondas de rollo (Fig. 26).
3.3 Flujo crítico
El flujo crítico ocurre bajo las siguientes condiciones (Fig. 30):
La condición del flujo crítico representa el límite entre el flujo subcrítico, para el cual F < 1, y el flujo supercrítico, para el cual F > 1. En el flujo de canales, las ondas dinámicas tienen dos componentes: (1) primario, y (2) secundario (Ponce and Simons, 1977). Las ondas primarias viajan con velocidades absolutas:
Las ondas secundarias viajan con velocidades absolutas:
Mientras que las ondas primarias siempre viajan en dirección aguas abajo, las ondas secundarias pueden viajar en dirección aguas arriba o aguas abajo, dependiendo de las condiciones del flujo. En el flujo subcrítico, w > u, y las ondas secundarias son capaces de viajar en dirección aguas arriba. En el flujo supercrítico, w < u, y las ondas secundarias no pueden viajar en dirección aguas arriba, por lo que siempre viajan aguas abajo. En la práctica, esto significa que el flujo subcrítico es controlado desde aguas abajo, ya que las perturbaciones superficiales son capaces de viajar en dirección aguas arriba. Por el contrario, el flujo supercrítico no puede ser controlado desde aguas abajo, debido a que las perturbaciones superficiales no son capaces de viajar en dirección aguas arriba. El flujo supercrítico siempre es controlado desde aguas arriba. El flujo crítico puede ocurrir de dos maneras:
3.3.1 La ecuación de Darcy-Weisbach para el flujo en canales La ecuación de Darcy-Weisbach es generalmente aplicable al flujo en conducto cerrados (tuberías). Para el flujo en tuberías, la longitud de fricción característica es el diámetro do. Para su aplicación al flujo en canales, la longitud de fricción característica es el radio hidráulico R:
El área de flujo de un conducto circular cerrado (un tubo que fluye lleno)
es A = π (do2/4),
y el perímetro mojado es
en la cual f = factor de fricción de Darcy-Weisbach, L = longitud del canal, V = velocidad media del flujo, g = aceleración de la gravedad. Bajo flujo permanente, la pendiente de la línea de energía en el flujo en canales es la misma que la pendiente de fricción, del lecho o del fondo. La pendiente es:
Para una sección transversal cualquiera, el número de Froude es:
en la cual la profundidad o tirante hidráulico D es: D = A /T. La Ecuación 76 se puede expresar en términos del número de Froude de la siguiente manera:
La Ec. 78 establece la proporcionalidad entre la pendiente de la línea de energía y el número de Froude. El factor de proporcionalidad es función del factor de fricción de Darcy-Weisbach y el factor de forma D/R. En un canal hidráulicamente ancho, para el cual D ≅ R, la Ec. 78 se reduce a:
En el caso de un canal hidráulicamente ancho, el factor de proporcionalidad entre la pendiente de la línea de energía y el número de Froude es solamente una función del factor de fricción de Darcy-Weisbach. Por conveniencia, para el flujo en canales se puede utilizar un factor de fricción modificado de Darcy-Weisbach f, igual a 1/8 del factor de fricción convencional. Por lo tanto, la ecuación modificada de Darcy-Weisbach aplicable al flujo en canales es:
3.3.2 La pendiente crítica La pendiente crítica es aquélla para la cual F = 1. La Ec. 78 para F = 1 es:
en la cual Sc = pendiente crítica. Para un canal hidráulicamente ancho, la Ec. 81 se reduce a:
Es decir:
Las Ecuaciones 81 a 83 demuestran que el factor de fricción
y la pendiente crítica están muy relacionados.
La Ec. 81 se utiliza para canales de sección transversal arbitraria, mientras que la En general:
en la cual Sc se puede definir por cualquiera de las Ecs. 81, 82, o 83. La Ecuación 84 es una modificación de la ecuación de Darcy-Weisbach aplicable al flujo en canales. En el flujo uniforme, esta ecuación muestra claramente el concepto de pendiente crítica. En el flujo gradualmente variado, la Ec. 84 permite un mejor entendimiento de los límites asintóticos de las curvas de remanso.
3.3.3 Ocurrencia del flujo crítico Tal como indica la Ec. 84, el flujo crítico ocurre cuando la descarga es tal que la pendiente crítica (pendiente de fricción) es igual a la pendiente de fondo. Esto es posible en un canal revestido, donde a medida que aumenta la descarga, la pendiente de fricción disminuye hasta coincidir con la pendiente de fondo. Por lo tanto, en un canal prismático artificial, es posible lograr profundidades de flujo críticas, e inclusive supercríticas. Los flujos supercríticos no son comunes, pero tampoco son imposibles. Por ejemplo, en el caso de la fricción de Chezy en los canales hidráulicamente anchos, las ondas de rollo se forman cuando el número de Vedernikov V = 1, el cual corresponde al número de Froude F = 2. Lo anterior no ocurre en un canal natural, donde el flujo es capaz de interactuar libremente con los materiales del fondo del canal, lo cual aumenta la pendiente "actual" o la fricción efectiva. En la práctica, la pendiente de fricción no disminuye hasta coincidir con la pendiente de fondo, por lo cual el flujo permanece subcrítico. De acuerdo a Jarrett (1982), es muy raro que se presente el flujo crítico o supercrítico en un canal natural (Fig. 32).
3.3.4 Cálculo del flujo crítico El cuadrado del número de Froude (Ec. 77) es:
Al sustituir V = Q /A y D = A /T se obtiene:
En el flujo crítico, F = 1, por lo cual la Ec. 86 se puede expresar de la siguiente manera:
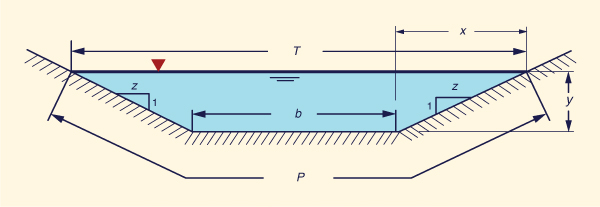
Con referencia a la Fig. 33, el ancho de superficie T es:
El área A del flujo es:
Sustituyendo las Ecs. 88 y 89 en la Ec. 87:
Dados g = aceleración de la gravedad, y los
datos de descarga Q, ancho de fondo b, y pendiente lateral
z [z:H a 1:V, Fig. 33], la profundidad crítica yc se encuentra resolviendo
la
La Ec. 90 se expresa como sigue:
La Ec. 95 es la fórmula general para el flujo crítico,
aplicable a canales trapezoidales. Para un canal
rectangular: Con el fin de simplificar la Ec. 95, se hace el cambio de variable x = yc , obteniéndose:
La solución de la Ec. 96 se obtiene
mediante un procedimiento iterativo.
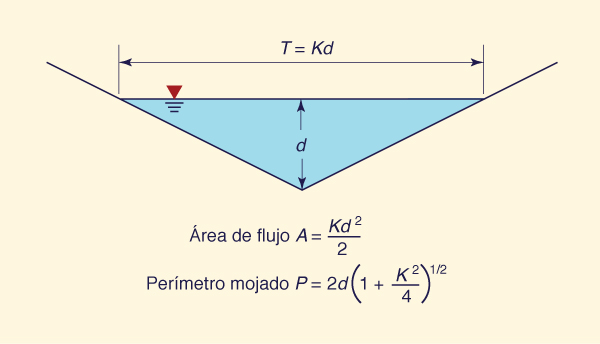
3.3.5 Profundidad crítica en un canal hidráulicamente ancho Para un canal hidráulicamente ancho, al igual que para un canal rectangular: Q = qb, y z = 0. Sustituyendo estos valores en la Ec. 95, se obtiene una expresión para la profundidad crítica yc en función solamente de la descarga por unidad de ancho q:
3.3.6 Vertederos de cresta ancha En un vertedero de cresta ancha, el flujo crítico ocurre cerca de la cresta. La descarga por unidad de ancho es:
Por definición, la profundidad crítica es igual a 2/3 de la carga total H medida sobre la cresta del vertedero:
Sustituyendo la Ec. 100 en la Ec. 99:
en la cual C es un coeficiente de descarga definido como sigue:
En unidades SI, C = 1.704; y en unidades acostumbradas en EE.UU., C = 3.087. Por diversas razones, un valor práctico de diseño Cd puede diferir del valor teórico C. La experiencia ha demostrado que el rango aproximado es: 0.8 ≤ Cd /C ≤ 1.3. La Figura 34 muestra un vertedero de cresta ancha para el cual Cd = 1.45 (unidades SI). En la práctica, H se toma como la elevación de la superficie del agua por encima de la cresta del vertedero. Esto asume que la velocidad de aproximación Va en una sección localizada suficientemente aguas arriba del vertedero es nula: Va = 0.
3.4 Flujo uniforme
El flujo uniforme se presenta únicamente en canales prismáticos. En el flujo uniforme, la profundidad de flujo, el área de flujo, la velocidad media, y la descarga (o caudal) son constantes a lo largo del canal. El término flujo de equilibrio se utiliza para describir la condición de flujo en canales no prismáticos (naturales) de sección transversal no uniforme, el cual es equivalente al flujo uniforme en canales prismáticos. En el flujo uniforme, todas las pendientes, la pendiente de fricción Sf, la pendiente de energía Se, la pendiente de la superficie del agua Sw, y la pendiente de fondo So, son constantes e iguales:
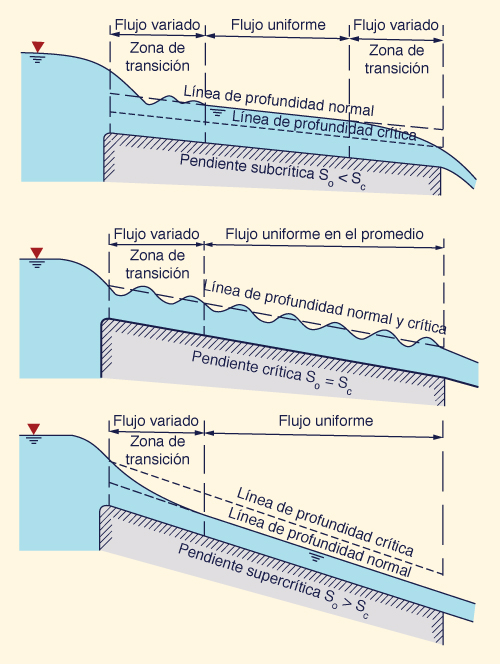
El flujo uniforme no permanente no existe; si el flujo es no permanente, entonces no es uniforme. Sin embargo, para el número de Vedernikov V = 1, el flujo uniforme se convierte en neutralmente estable, lo cual conduce a las ondas de rollo. Esta condición es la inestabilidad del flujo uniforme descrita por Chow (1959). Cuando V < 1, las perturbaciones del flujo se atenúan y, por consiguiente, las ondas de rollo no se desarrollan. Desde un punto de vista mecánico, el flujo uniforme ocurre en un volumen de control cuando la fuerza de fricción es igual a la fuerza gravitacional. En ausencia de controles de sección, todos los flujos en canales tienden a ser uniformes; podría decirse que a la Naturaleza le gusta el flujo uniforme. En el flujo uniforme, la característica única de la curva de gasto, es decir, la singularidad de la relación descarga-área (o descarga-profundidad), lo califica como control. Por lo tanto, el flujo uniforme crítico es un tipo de control muy fuerte. La profundidad del flujo uniforme se conoce como profundidad normal. La Figura 35 muestra la formación de flujo uniforme en un canal relativamente largo. La figura superior representa el flujo normal subcrítico, con las secciones de control aguas arriba y aguas abajo. La figura central representa el flujo crítico, con las secciones de control aguas arriba y aguas abajo. La figura inferior representa el flujo normal supercrítico, con la sección de control aguas arriba únicamente.
3.4.1 Fórmula de Chezy Para derivar la fórmula de Chézy, el esfuerzo cortante τb desarrollado a lo largo del fondo del canal se modela con la siguiente ley de fricción cuadrática:
en la cual ρ = densidad de la masa,
f =
factor de fricción,
y La fuerza de fricción desarrollada a lo largo del perímetro mojado P de un volumen de control de longitud L es (Fig. 36):
El peso del agua contenido en el volumen de control es W. Esta fuerza gravitacional se resuelve a lo largo de la dirección del movimiento de la siguiente manera:
Para un canal de pendiente pequeña: sen θ ≅ tan θ = S. Por lo tanto:
Igualando las fuerzas de fricción (Ec. 105) y gravitacional (Ec. 107):
lo cual se reduce a:
en la cual R = radio hidráulico. Resolviendo para V:
en la cual C = coeficiente de Chézy:
Por lo tanto, el factor de fricción f en la Ec. 73 es:
La Ec. 111 es la fórmula de Chézy. De la Ec. 110 se puede derivar una variante de la fórmula de Chézy:
lo cual equivale a:
El último término de esta ecuación es el cuadrado del número de Froude. Por lo tanto:
Para un canal hidráulicamente ancho, D ≅ R, y la Ec. 116 se reduce a:
La Ec. 117 es la ecuación modificada de Chezy. Nótese que es la misma que la Ec. 80, la ecuación modificada de Darcy-Weisbach. La Tabla 10 muestra los valores correspondientes de f, f y el coeficiente de Chézy.
3.4.2 Fórmula de Manning La fórmula de Manning, en unidades SI, es la siguiente:
en la cual n = coeficiente de fricción de Manning, factor de fricción, o simplemente n de Manning. A fin de comparar con la fórmula de Chezy, la ecuación de Manning se expresa como sigue:
La relación entre los coeficientes de Manning y Chezy se encuentra comparando las Ecs. 111 y 119:
La Ec. 120 implica que mientras C varía con el radio hidráulico, el valor de n es constante. Esto puede ser aproximadamente cierto para los canales prismáticos (artificiales), pero por lo general no lo es para los canales naturales. En estos últimos, el valor de n puede variar con el nivel de la superficie del agua y la profundidad del flujo. Esto es atribuible a:
En términos de rugosidad relativa y rugosidad absoluta, la expresión general para el n de Manning es (Chow, 1959):
Strickler utilizó una constante (0.0342) para la rugosidad relativa f(R/ks), y
el tamaño medio de la partícula
d50 (en pies) como el diámetro representativo
de grano, para derivar la ecuación
La Tabla 11 muestra los valores de n de Manning calculados con la fórmula de Strickler (Ec. 91).
3.4.3 Estimación empírica del n de Manning No existe un procedimiento exacto para estimar el n de Manning. Las siguientes son algunas recomendaciones probadas en la práctica:
Chow (1959) ha presentado una colección ilustrada de veinticuatro (24) canales para los cuales los valores de n han sido establecidos. El rango de valores documentados por Chow es de n = 0.012 (un canal revestido con placas de concreto), a n = 0.150 (un río natural en suelo de arcilla arenosa, con taludes y fondo irregulares). Chow documentó valores tan bajos como n = 0.008 (plástico acrílico) y tan altos como n = 0.200 (llanuras de inundación de corrientes naturales, con vegetación densa en el verano) (Tabla A-4). Estos valores se aplican al flujo turbulento.
Barnes (1967) ha presentado una colección
ilustrada a colores de cincuenta (50) cauces fluviales para los cuales el n de Manning
ha sido calculado.
La colección de Barnes
se puede ver en línea en
Manning's n Pictorial.
El valor más pequeño de n documentado por Barnes es
En la práctica, el valor de n de Manning varía en forma considerable. En los cauces naturales puede variar desde aproximadamente 0.02
para algunos ríos muy grandes con fondo liso
Cowan (1956) ha desarrollado una metodología racional para
la estimación del n de Manning.
en la cual:
La Tabla 13 muestra los valores que deben ser usados en la Ec. 123.
3.4.4 Cálculo del flujo uniforme
De la Fig. 33 se deduce la siguiente proporción: z /1 = x /y. Por lo tanto, el ancho de superficie T es:
El área de flujo A es:
El perímetro mojado P es:
Simplificando:
A partir de la ecuación de Manning, la descarga Q es:
en la cual k = 1 en unidades SI, y k = 1.486 en el sistema de unidades acostumbradas en EE.UU. Dado que R = A /P, la Ec. 128 se reduce a:
Sustituyendo las Ecs. 125 y 127 en la Ec. 129:
Simplificando:
La profundidad o tirante normal y se calcula por medio de la Ec. 131 con los siguientes datos de entrada: (1) descarga Q, (2) ancho de fondo b, (3) talud z [z: H a 1: V, Fig. 33], (4) pendiente de fondo S, y (5) n de Manning. Por lo tanto, con las Ecs. 124 y 125:
La Ecuación 131 es la fórmula general para el flujo uniforme o normal, aplicable a los canales prismáticos de sección transversal trapezoidal. Para un canal rectangular: z = 0; asimismo, para un canal triangular de sección simétrica: b = 0. Para resolver la Ec. 131, se expresa de la siguiente manera:
Sustituyendo la variable x = y:
La Ecuación 135 se resuelve mediante un procedimiento iterativo. A continuación se describe un algoritmo basado en el valor de la función. La Figura 42 es un ejemplo del flujo normal.
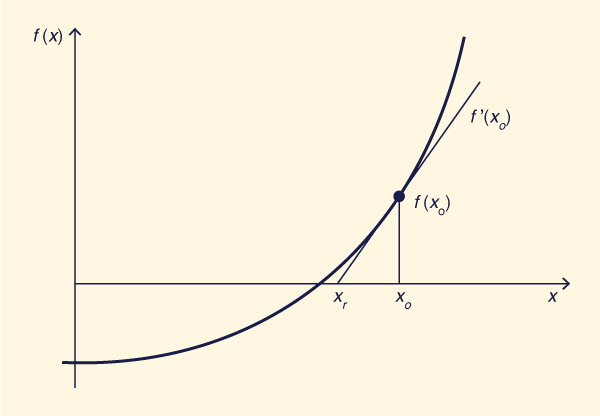
El algoritmo anteriormente descrito utiliza únicamente el valor de la función para la aproximación a la raíz. Como alternativa, la aproximación de Newton basada en la tangente converge más rápidamente. Sin embargo, para que el método de Newton funcione correctamente, es necesario primero acercarse a la raíz usando la iteración basada en el valor de la función. De lo contrario, es probable que el método de Newton no converja. Con referencia a la Fig. 43, el valor de la tangente en xo es:
en la cual xo = valor de prueba de x, f(xo) = valor de la función en xo, xr = nuevo valor de x, que se aproxima más a la raíz.
Resolviendo para xr de la Ec. 136:
Como se muestra en la Fig. 43, cuando f (xo) aumenta con xo (como es el caso de la Ec. 137) al pasar por la raíz, el valor de la función y el valor de la tangente son positivos; por lo tanto, el denominador de la Ec. 136 también es positivo, y xr se encuentra a la izquierda de xo. Con cada iteración subsecuente, la raíz es aproximada en forma de zig-zag, hasta que la tolerancia especificada sea satisfecha. Se puede mostrar fácilmente que la Ec. 137 también se aplica cuando f (xo) disminuye a medida que xo aumenta, como en el caso del flujo crítico, ver la Sección 4.2. El valor de f '(x) es:
Simplificando:
El procedimiento para la aproximación de Newton se describe a continuación.
3.5 Flujo permanente gradualmente variado El flujo permanente es gradualmente variado cuando la descarga Q es constante pero las demás variables hidráulicas (A, V, D, R, P, etc.) varían gradualmente en el espacio. Las suposiciones básicas de flujo permanente gradualmente variado son:
Otras suposiciones del flujo gradualmente variado son:
3.5.1 Ecuación del flujo permanente gradualmente variado
En el flujo gradualmente variado, el gradiente de la carga hidráulica es (Fig. 44):
El signo negativo para la pendiente de fricción Sf es necesario ya que la dirección de flujo es de izquierda a derecha, mientras que por costumbre, la derivada se toma de derecha a izquierda. La pendiente de fricción es:
en la cual ΔL = longitud del tramo del canal. El gradiente de la energía específica es:
El gradiente del lecho del canal, o la pendiente del fondo, es:
Combinando las Ecs. 142 y 144:
En el flujo permanente: Q = V A = constante. Por lo tanto:
Dado que dA/dy = T, el ancho de la superficie libre (Fig. 25):
Por lo tanto, el gradiente de profundidad es:
La pendiente de fricción basada en la ecuación de Chezy es:
Debido a que R = A / P :
Sustituyendo la Ec. 153 en la Ec. 151, el gradiente de profundidad es:
El cuadrado del número de Froude es:
Substituyendo la Ec. 156 en la Ec. 155:
Sustituyendo la Ec. 113 en la Ec. 157:
Por lo tanto, el gradiente de profundidad (dy/dx) es una función de:
Para dy/dx = 0, la Ec. 158 se reduce a la ecuación de flujo uniforme:
Para F = 1, la Ec. 159 se reduce al flujo uniforme crítico:
en la cual Sc = pendiente crítica, es decir, la pendiente del canal para la cual el flujo es crítico. En términos de la pendiente crítica, el gradiente de profundidad es:
Para (P / T ) ≅ (Pc / Tc ), es decir, para una relación constante (P / T), la Ec. 161 se reduce a:
El gradiente de profundidad se puede escribir como sigue:
Sustituyendo la Ec. 163 en la Ec. 162:
La Ecuación 164 (o la Ec. 162) es la ecuación
de flujo permanente gradualmente variado (Fig. 45).
3.5.2 Curvas de remanso
En la Ecuación 164, el signo del lado izquierdo (SLI) es el de Sy (numerador), ya que Sc (denominador) es siempre positivo (la fricción es siempre positiva). El signo de Sy puede ser una de tres posibilidades:
En el lado derecho de la Ec. 164, hay tres posibilidades para el numerador (USDA Soil Conservation Service, 1971):
Asimismo, existen tres posibilidades para el denominador:
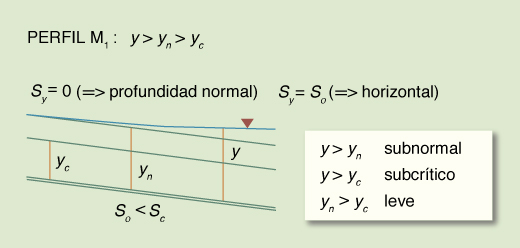
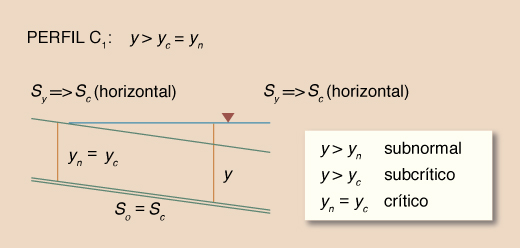
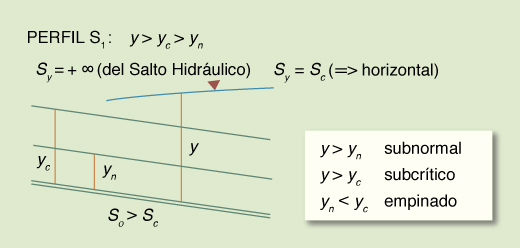
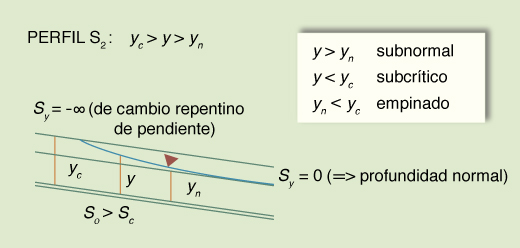
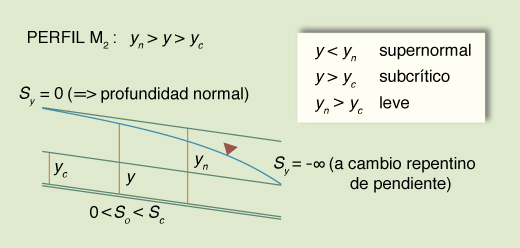
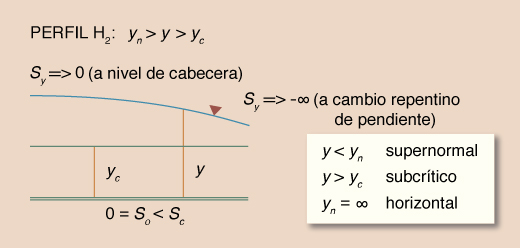
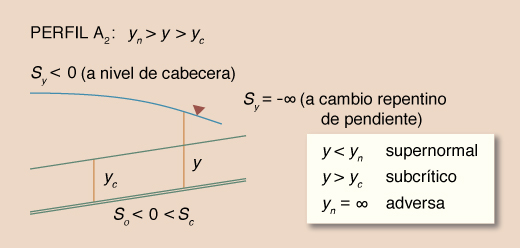
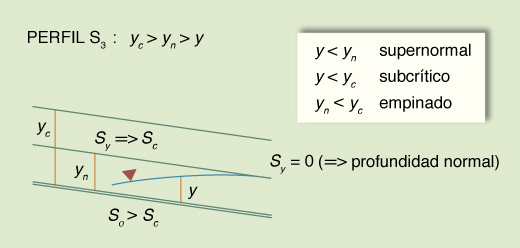
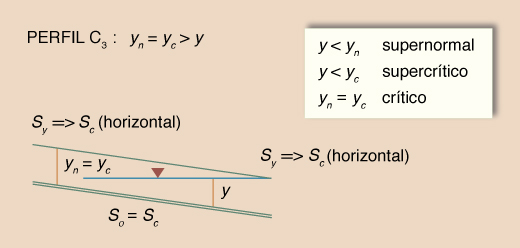
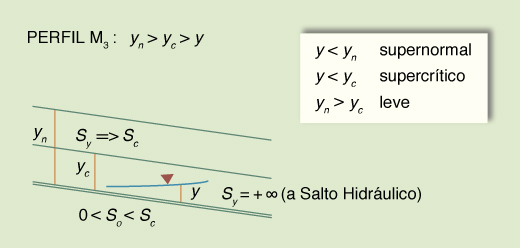
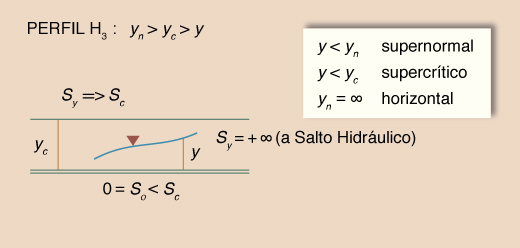
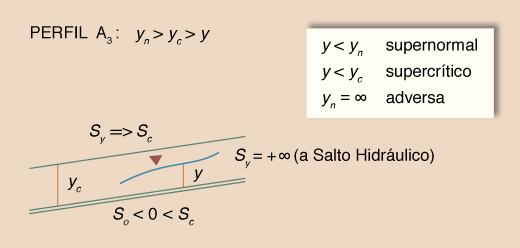
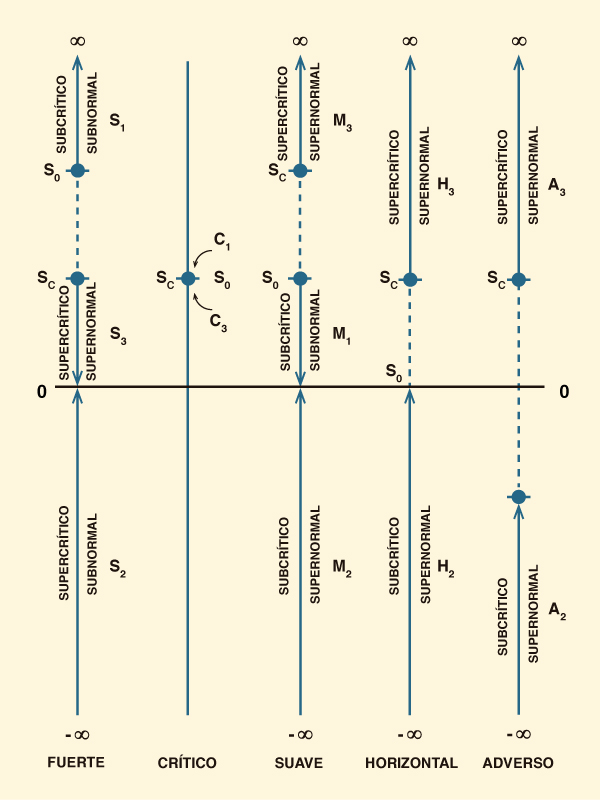
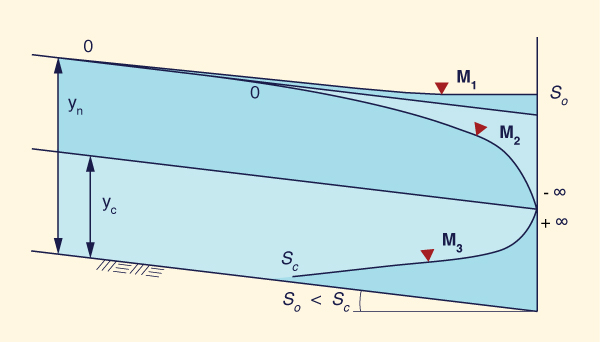
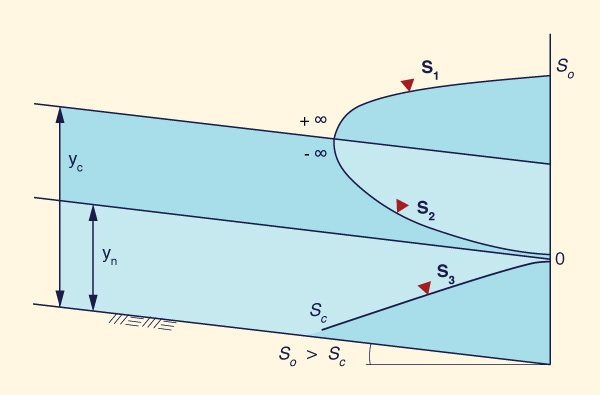
Dadas las desigualdades mencionadas, surgen tres tipos o familias de perfiles de superficie del agua, los cuales se muestran en la Tabla 14. La Tabla 15 muestra un resumen de los perfiles. El número total de perfiles es 12.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||