La onda cinemática desmitificada, Victor M. Ponce

Fig. 1 Río Alto Paraguay en Porto Murtinho, Mato Grosso do Sul, Brasil,
el cual presenta un hidrograma de inundación de un año de duración (el máximo posible),
claramente la onda de inundación cinemática por excelencia.

LA ONDA CINEMÁTICA DESMITIFICADA

Víctor M. Ponce

Profesor Emérito de Ingeniería Civil y Ambiental

Universidad Estatal de San Diego, San Diego, California

11 de mayo de 2024

RESUMEN. Hemos aclarado el concepto de onda cinemática y su aplicación en la ingeniería hidráulica e hidrológica. Nos hemos centrado en la naturaleza de las ondas cinemáticas y su importancia como método apropiado para modelar ondas de inundación. Dada la capacidad de la onda cinemática difusiva para explicar adecuadamente la difusión de la onda, se considera que su aplicabilidad mejora sustancialmente. Otros tipos de ondas, como las ondas cinemático-dinámicas mixtas y las ondas dinámicas de Lagrange, carecen del tamaño (escala) y/o permanencia de las ondas cinemáticas. Por lo tanto, consideramos que la onda cinemática es el método más apropiado para modelar la propagación de ondas de inundación.

1. INTRODUCCIÓN

Las ondas cinemáticas continúan siendo motivo de controversia (Ponce, 1991). Si bien se han utilizado en la teoría y la práctica durante casi seis décadas (desde la década de 1960), a menudo no se comprende completamente sus ventajas y desventajas. En consecuencia, el objetivo del presente artículo es arrojar luz adicional sobre el tema de las ondas cinemáticas, explicando su origen, naturaleza, características, y utilidad. Completamos el tratamiento considerando las formas de modelar ondas cinemáticas en forma adecuada y precisa.

2. ORIGEN DE LAS ONDAS CINEMÁTICAS

El fundamento teórico de lo que actualmente conocemos como onda cinemática se originó en el trabajo pionero de Lighthill y Whitham (1955), quienes formularon matemáticamente un cierto tipo de movimientos ondulatorios que aparentemente no eran de naturaleza dinámica. Estas ondas podrían interpretarse fácilmente como cinemáticas, ya que se derivan deliberadamente de la ecuación de continuidad del movimiento unidimensional del flujo en canales. Además, a diferencia de las ondas dinámicas, que característicamente transportan energía, las ondas cinemáticas transportan masa. Diferentes términos en las ecuaciones de gobierno describen cada una de estas ondas, cinemática y dinámica; por lo tanto, sus propiedades de celeridad y atenuación difieren sustancialmente (Ponce y Simons, 1977).

Boussinesq (1877) menciona a Breton (1867) y Graëff (1875) como pioneros de la teoría. Chow (1959) atribuye a Kleitz (1877) el mérito de ser el primero en derivar la fórmula para la celeridad de la onda cinemática. Unos años más tarde, Seddon (1900) evaluó dicha celeridad a partir de mediciones en los ríos Mississippi y Missouri, concluyendo que la celeridad (m) de una onda cinemática en una sección transversal dada es igual a la pendiente (dQ/dh) de la curva de gasto, dividida por el ancho (W). En la práctica, la fórmula de Seddon para la celeridad de una onda cinemática se ha denominado ley de Kleitz-Seddon, o simplemente ley de Seddon. Más de 50 años después, los hallazgos de Seddon fueron ampliamente confirmados por Lighthill y Whitham (1955).

3. NATURALEZA DE LAS ONDAS CINEMÁTICAS

Las ondas cinemáticas son ondas de inundación. La afirmación opuesta también es cierta: Las ondas de inundación son cinemáticas; aunque con algunas excepciones que trataremos en la Sección 5. Lighthill y Whitham (1955) expresaron esto claramente cuando afirmaron: "En algunas aplicaciones, incluido el caso de las ondas de inundación, las ondas cinemáticas y las ondas dinámicas son posibles juntas. Sin embargo, las ondas dinámicas tienen una velocidad de onda mucho mayor y también una atenuación rápida; por lo tanto, aunque cualquier perturbación envía alguna señal aguas abajo a la velocidad de onda normal para las ondas de gravedad [sic], esta señal es demasiado débil para ser notada en cualquier momento a una distancia aguas abajo, y la señal principal llega en forma de onda cinemática a una velocidad mucho más lenta". Así, en muchos problemas de interés práctico, se ve que las ondas dinámicas están completamente subordinadas a las ondas cinemáticas, las cuales viajan sólo aguas abajo, con masa y volumen significativamente mayores y a una velocidad mucho más lenta.

Ponce y Simons (1977). han aclarado las diferencias entre los distintos tipos de ondas en el flujo unidimensional en canales abiertos. Ellos utilizaron la teoría de la estabilidad lineal para determinar las funciones de celeridad y atenuación para todo tipo de ondas en aguas poco profundas, incluidas: (1) cinemáticas, (2) cinemático-dinámicas mixtas y (3) dinámicas. El elemento unificador es, sin duda alguna, el número de onda adimensional σ_{_*}, definido multiplicando el número de onda aplicable (2π /L) por la longitud de referencia del canal L_o, es decir, la longitud que le tomaría al flujo de equilibrio perder una carga igual a su profundidad.

Las ondas cinemáticas son las de Seddon (1900), mientras que las ondas dinámicas son las de Lagrange (1877). [Nótese que estas últimas son efectivamente las "ondas de gravedad" a las que se refieren Lighthill y Whitham; ver el párrafo anterior]. Las ondas cinemático-dinámicas mixtas son aquéllas que se encuentran en el centro-derecha del espectro del número de onda adimensional formulado por Ponce y Simons (1977) (Fig. 2). Estas ondas "mixtas" aparecieron en los modelos numéricos desarrollados a partir de la década de 1970 para resolver las ecuaciones completas de St. Venant (Fread, 1985). Estos modelos han sido ampliamente denominados "ondas dinámicas", aunque el nombre es un tanto inapropiado, pues ha llevado a confusión con las ondas clásicas de Lagrange (1877).

Ponce y Simons (1977)

Fig. 2 Celeridad de onda relativa adimensional c_{_{_r}}_{_{_*}} vs número de onda adimensional σ_{_{_*}}.

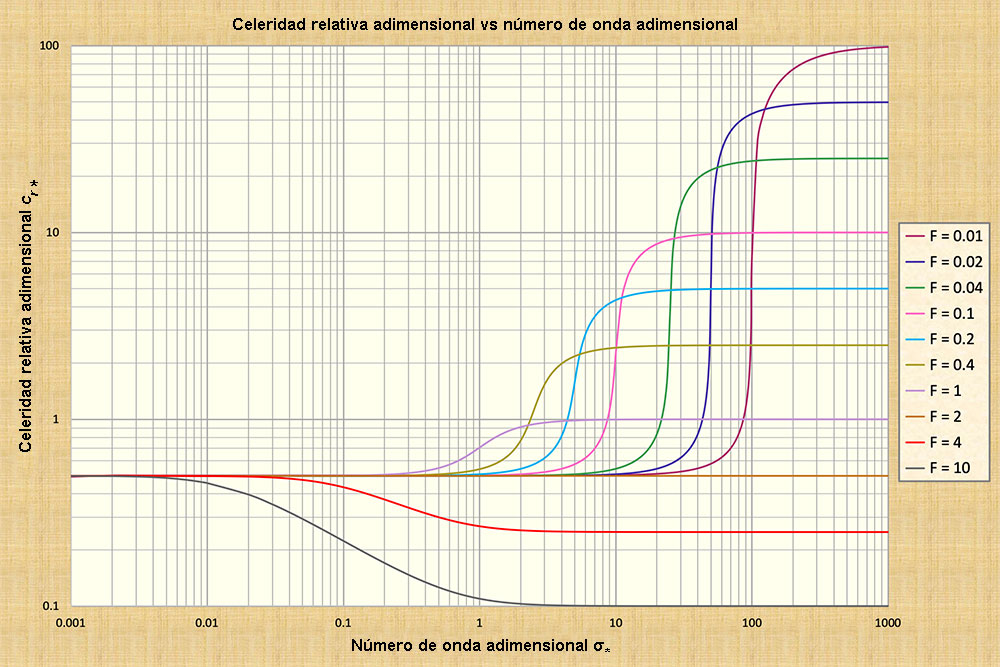
Reiterando, las ondas cinemáticas de Seddon, las cuales se encuentran hacia la izquierda del espectro del número de onda adimensional, presentan una celeridad de onda constante y, por lo tanto, no son difusivas. Siguiendo el mismo razonamiento, las ondas dinámicas de Lagrange, situadas hacia la derecha, tampoco son difusivas. Sin embargo, se ha demostrado que las ondas cinemático-dinámicas mixtas, que se encuentran hacia el centro-derecha y que presentan una celeridad variable, son fuertemente difusivas. La cantidad de difusión varía con el número de Froude predominante, correspondiendo una mayor difusión a los números de Froude más bajos, siempre que este último permanezca por debajo del valor umbral F = 2, aplicable para la fricción de Chezy en canales hidráulicamente anchos (Fig. 2).

Para terminar, reiteramos que Lighthill y Whitham (1955) ahondaron sobre la competencia entre ondas cinemáticas y mixtas, para mostrar cuán completamente subordinadas están estas últimas a las primeras en el caso de mayor interés práctico, es decir, cuando la velocidad del flujo es baja en el régimen subcrítico. Esto subraya lo inadecuado que son las ondas mixtas como base para los cálculos de ondas de inundación y, por extensión, enfatiza la importancia práctica de las ondas cinemáticas.

4. ONDAS CINEMÁTICAS CON DIFUSIÓN

Y aquí es donde la trama se complica! Las ondas cinemáticas se denominan así porque ocurren aparentemente en ausencia de inercia, excluyendo también el gradiente de presiones [Tabla 1, Fila 1]. Por el contrario, la onda dinámica (exactamente lo contrario, a juzgar por sus componentes) se produce significativamente en ausencia únicamente de fricción y gravedad [Fila 4].

Cabe mencionar que la existencia del gradiente de presiones complica la definición de onda cinemática. Este hecho llevó a Lighthill y Whitham (1955) < a distinguir entre dos tipos de ondas cinemáticas: (1) aquéllas con fricción y gravedad únicamente, excluyendo la inercia y el gradiente de presiones, denominadas simplemente ondas cinemáticas [Fila 1]; y (2) aquéllas con fricción, gravedad y gradiente de presiones, excluyendo sólo la inercia, denominadas ondas cinemáticas con difusión o, para abreviar, ondas de difusión o difusivas [Fila 2] (Ponce y Simons, 1977). Las ondas mixtas cinemático-dinámicas, que presentan todos los términos de la ecuación de movimiento [Fila 3], completan la lista de ondas de aguas poco profundas en la práctica de la ingeniería hidráulica.

Tabla 1. Tipos de ondas en flujo no permanente en canales abiertos.
No.	Onda	Términos de la ecuación de movimiento que participan en la onda.					Nombre común
No.	Onda	Inercia local	Inercia convectiva	Gradiente de presiones	Fricción	Gravedad	Nombre común
1	Cinemática				✓	✓	Cinemática
2	Cinemática con difusión			✓	✓	✓	Difusión
3	Cinemático-dinámica mixta	✓	✓	✓	✓	✓	Mixta
4	Dinámica (Lagrange)	✓	✓	✓			Dinámica

Observamos que dado que las ondas cinemáticas no se atenúan [Fila 1], y que las ondas de difusión sí lo hacen [Fila 2], se deduce que el término gradiente de presiones debe ser el responsable de la atenuación, es decir, la limitada cantidad de difusión experimentada por ondas de inundación típicas. Esta conclusión ha sido ampliamente confirmada por la teoría y la práctica.

Hemos establecido que las ondas dinámicas (Lagrange) [Fila 4] son demasiado pequeñas para constituir ondas de inundación. También hemos establecido que las ondas cinemático-dinámicas mixtas [Fila 3] son demasiado difusivas para desempeñar un papel práctico en aplicaciones de ondas de inundación. Por lo tanto, sólo las ondas cinemáticas [Fila 1] y las de difusión [Fila 2] probablemente sean lo suficientemente voluminosas y a la vez permanentes como para ser modelos apropiados de la propagación de ondas de inundación.

Ponce (2023a) ha calculado las cantidades precisas de difusión de las ondas de inundación mostradas en la Tabla 2. Para este propósito, el rango de números de onda adimensionales aplicables varía cinco órdenes de magnitud, desde σ_{_{_*}} = 0.0001 hasta σ_{_{_*}} = 10 (Fig. 2). Para σ_{_{_*}} = 0.0001, las ondas son cinemáticas y experimentan atenuación cero; para σ_{_{_*}} = 0.001, las ondas son cinemáticas a difusivas, experimentando muy poca atenuación (0.002); para σ_{_{_*}} = 0.01, las ondas son de difusión, experimentando una atenuación pequeña pero perceptible (0.021); para σ_{_{_*}} = 0.1, las ondas son definitivamente de difusión, experimentando una atenuación considerable (0.189); para σ_{_{_*}} = 1, las ondas son mixtas, experimentando una atenuación muy fuerte (0.877); y para σ_{_{_*}} = 10, las ondas se han atenuado completamente (1.0), es decir, �han dejado de existir!

Tabla 2. Cantidades de difusión de ondas a lo largo del espectro de números de onda adimensional.
[1]	[2]	[3]	[4]	[5]	[6]
No.	*Número de onda adimensional σ_{_{_}}**	Decremento logarítmico δ_d	e^δ_d	Atenuación de onda (1 - e^δ_d)	Tipo de onda
0	0.0001	0.00020944	1	0	Cinemática
1	0.001	0.0020944	0.998	0.002	Cinemática a difusión.
2	0.01	0.020944	0.979	0.021	Difusión
3	0.1	0.20944	0.811	0.189	Difusión
3a	0.17	0.35604	0.700	0.300	Difusión a mixta
4	1	2.0944	0.123	0.877	Mixta
5	10.	20.944	0	1.0	Mixta

Confirmamos que las ondas cinemáticas no están sujetas a atenuación, aunque pueden sufrir cambios de forma debido a la no linearidad (Ponce y Windingland, 1985). También confirmamos que para el valor medio del número de onda adimensional σ_{_{_*}} > 0.17, la atenuación de la onda es mayor que 0,30 (30%). Este umbral es considerado como el límite entre las ondas de difusión (de difusión de onda limitada, menos del 30%) y las ondas mixtas (de difusión de onda ilimitada, que podría llegar a 1,0 (100%) (Natural Environment Research Council, 1975). Por lo tanto, se confirma que las ondas mixtas son muy fuertemente difusivas y, en la mayoría de los casos de interés práctico, es probable que no estén allí para que podamos calcularlas (Ponce, 1992).

Antes de concluir el tema de las ondas cinemáticas en comparación con las ondas de inundación, nos queda poner en el contexto adecuado la naturaleza de las ondas de rollo. �Estas ondas son cinemáticas o dinámicas? Ya ha quedado firmemente establecido que las ondas de rollo ocurren en canales revestidos empinados de sección transversal rectangular, cuando la celeridad de la onda cinemática (celeridad de Seddon) excede la celeridad de la onda dinámica (celeridad de Lagrange) (Craya, 1952). En el flujo inestable en canales abiertos, esta condición se presenta cuando el número de Vedernikov excede el valor umbral V = 1, típicamente en flujos empinados de sección transversal rectangular (Ponce, 1991b). Téngase en cuenta que esta condición es equivalente a un número de Froude F = 2, aplicable a la fricción de Chezy en canales hidráulicamente anchos.

La cuestión de si un evento de onda de rollo puede considerarse una onda de inundación es una evaluación que es mejor dejar para cada caso individual. Si las ondas de rollo logran superar los límites del canal, pueden considerarse peligrosas y, por lo tanto, una especie de "onda de inundación". De lo contrario, si las ondas de rollo permanecen restringidas dentro de los límites del canal, dentro de lo razonable, no pueden considerarse ondas de inundación. El riesgo de inundación que surge de un evento de onda de rollo tiende a ser altamente específico, y las determinaciones individuales probablemente varíen en el espacio y en el tiempo.

Para finalizar, afirmamos que las ondas cinemáticas y de difusión encuentran su aplicación práctica en la propagación de ondas de inundación. Éstas son generalmente masivas y de movimiento lento, a diferencia de las ondas dinámicas (Lagrange), que no lo son. Además, las ondas mixtas son tan difusivas que desaparecen rápidamente y su masa se une a las ondas cinemáticas subyacentes, las cuales continúan creciendo a medida que se propagan aguas abajo.

5. USO DE LAS ONDAS CINEMÁTICAS Y DIFUSIVAS

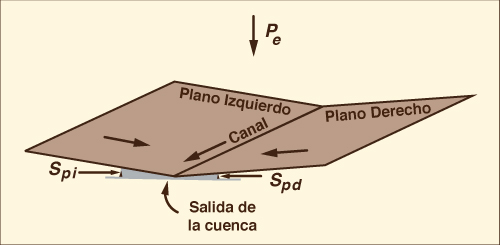
Las ondas cinemáticas encuentran su mejor aplicación en la propagaión de las ondas de inundación. Sin embargo, también se han utilizado en el tránsito de flujos de superficie libre, las cuales debido a su escala generalmente reducida, pueden no constituir ondas de inundación. Wooding (1965) fue el primero en aplicar la onda cinemática en modelos numéricos de flujo sobre el terreno, utilizando una configuración de libro abierto que ha sido ampliamente reconocida como plano de Wooding (Fig. 3).

Fig. 3 El plano de Wooding, una configuración geométrica de libro abierto
utilizada en la modelación del flujo de superficie libre.

La aplicación más general de las ondas cinemáticas es el tránsito de las ondas de inundación, es decir, el cálculo numérico de la progresión de una onda a medida que viaja aguas abajo, a lo largo de una corriente, río o canal. La onda de inundación real puede ser una onda cinemática, con difusión nula o, en su defecto, una onda de difusión, con una cantidad pequeña pero perceptible de difusión, es decir, de atenuación o disipación (Tabla 2). Las ondas de inundación se forman así como la aglomeración de un número infinito de ondas mixtas de diferentes tamaños, con sus fuertes tendencias difusivas actuando para convertir las ondas mixtas, de escala relativamente pequeña, en una onda de inundación cinemática o de difusión mucho más grande (Lighthill y Whitham, 1955).

La propiedad que caracteriza a las ondas de inundación es que generalmente son masivas y están sujetas a poca o ninguna atenuación. En una aplicación práctica, las contribuciones de los flujos laterales, de todas las fuentes, aseguran que las ondas de inundación continúen aumentando en masa y tamaño, volviéndose más masivas y, por lo tanto, menos atenuantes, a medida que la onda se propaga aguas abajo.

Actualmente se utilizan modelos numéricos de ondas cinemáticas y difusivas. Estos modelos han existido desde la década de 1970, pero no están exentos de problemas. Las soluciones analíticas de la ecuación de la onda cinemática carecen de difusión; las soluciones numéricas, sin embargo, muestran invariablemente una cantidad perceptible. Esto último se atribuye a la difusión que se origina en el propio esquema numérico, ya que aquélla está ausente en la ecuación de la onda cinemática. Los esquemas que se basan en la ecuación de onda cinemática no tienen forma de relacionar la difusión numérica observada con la difusión física real (U.S. Army Corps of Engineers, 2024). Por lo tanto, son, en el mejor de los casos, conceptuales, y generalmente no alcanzan la precisión que normalmente se esperaría en un modelo matemático con base física.

El dilema fue resuelto por Cunge (1969), quien propuso hacer coincidir la difusión numérica del esquema mismo con la difusión física de la ecuación de onda cinemática relacionada con la difusión, es decir, la ecuación de la onda de difusión. Este desarrollo condujo al método de Muskingum-Cunge para el enrutamiento de inundaciones (Ponce, 2014), una mejora del método clásico Muskingum (1938).

La característica de independencia de la cuadrícula (en Inglés, grid independence) una ventaja importante del método Muskingum-Cunge, lo distingue de los métodos basados únicamente en la ecuación de la onda cinemática (Ponce, 1986; Ponce, 2023b). Por lo tanto, los modelos de flujo de superficie con componente de onda de difusión son claramente el siguiente paso en el modelado de cuencas (Aguilar, 2014).

6. UN EJEMPLO SINGULAR

A estas alturas, seguramente el lector se habrá familiarizado completamente con la naturaleza y utilidad de las ondas cinemáticas y, por extensión, de las ondas difusivas. Todas las ondas de inundación dignas de ese nombre están sujetas a modelación utilizando la teoría de la onda cinemática. Debería ser obvio que cuanto mayor es la cuenca, más cinemática es la onda y más daño puede causar una inundación. Las ondas cinemáticas no sólo son grandes, sino que también decaen o se atenúan lentamente y, en algunos casos, carecen completamente de atenuación (consultar la Tabla 2, Fila 0). No es de extrañar que investigadores como Seddon (1900) pudieran documentar únicamente ondas cinemáticas en su trabajo pionero. Consideramos que Lighthill y Whitham (1955) fueron muy oportunos al exponer la teoría de ondas cinemáticas, lo que facilitó ampliamente las investigaciones posteriores. Desafortunadamente, el subtítulo del artículo de Lighthill y Whitham es algo confuso: "Movimiento de inundaciones en ríos largos". Tal vez debería decir: "Movimiento de inundaciones en todos los ríos".

Concluimos centrándonos en el ejemplo de la inundación anual del río Alto Paraguay, que drena 496.000 kilómetros cuadrados en las llanuras del Centro Oeste de Brasil y el Este de Bolivia. La parte central de la cuenca drena un delta continental, con pendientes muy suaves de los ríos y arroyos, las cuales se han documentado tan bajas como 0,00001, es decir, 1 cm/km. La onda cinemática resultante es tan grande que la onda de inundación medida en Porto Murtinho, Mato Grosso do Sul, normalmente tiene sólo un pico anual, constituyendo básicamente "la onda de inundación cinemática por excelencia" (Fig. 4).

Fig. 4 Río Alto Paraguay en Porto Murtinho, Mato Grosso do Sul, Brasil, en el cual el hidrograma de inundación tiene una duración de un año.

7. OBSERVACIONES FINALES

Hemos aclarado el concepto de onda cinemática y sus aplicaciones en la ingeniería hidráulica e hidrológica. Nos hemos centrado en la Naturaleza de las ondas cinemáticas y su importancia como método apropiado para modelar ondas de inundación. Dada la capacidad de la onda cinemática para explicar adecuadamente la difusión, su aplicabilidad mejora sustancialmente. Otros tipos de ondas, como las mixtas cinemático-dinámicas y las ondas dinámicas de Lagrange, carecen del tamaño (escala) y/o permanencia de las ondas cinemáticas. Por lo tanto, la onda cinemática se considera el método más apropiado para modelar la propagación de ondas de inundación.

BIBLIOGRAFÍA

Aguilar, R. 2014. Diffusion wave modeling of catchment dynamics using online calculation. M.S. thesis, Department of Civil, Construction, and Environmental Engineering, San Diego State University, San Diego, California, Spring.

Boussinesq. J. 1877. Essai sur la théorie de eaux courantes (Essay on the theory of running waters), Mém. prés. Acad.Sci., Paris, 23.

Breton, Ph. 1867. Sur les barrages de retenue des graviers dans les gorges des torrents (On gravel retention dams in torrent gorges), Paris.

Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, New York, NY.

Craya, A. 1952. The criterion for the possibility of roll wave formation. Gravity Waves, National Bureau of Styards Circular No. 521, National Bureau of Styards, Washington, D.C. 141-151.

Cunge, J. A. 1969. On the Subject of a Flood Propagation Computation Method (Muskingum Method). Journal of Hydraulic Research, 7(2), 205-230.

Fread, D. L. 1985. "Channel Routing," in Hydrological Forecasting, M. G. Anderson y T. P. Burt, eds., Wiley, New York.

Graëff, J. 1875. Sur l'application des courbes de débits à l'etude du regime des rivières (On the application of flow curves to the study of the regime of rivers), Mém. prés. Acad.Sci., Paris, 21.

Kleitz, M. 1877. Note sur la théorie du mouvement non permanent des liquides et sur application à la propagation des crues des rivières (Note on the theory of unsteady flow of liquids y on application to flood propagation in rivers), Annales des ponts et chaussées, ser. 5, Vol. 16, 2e semestre, 133-196.

Lagrange, J. L. de. 1788. Mécanique analytique, Paris, part 2, section II, article 2, 192.

Lighthill, M. J. y G. B. Whitham. 1955. On kinematic waves. I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.

McCarthy, G.T. . 1938. "The Unit Hydrograph y Flood Routing," unpublished manuscript, presented at a Conference of the North Atlantic Division, U.S. Army Corps of Engineers, June 24. (Cited by V. T, Chow's text "Open-channel Hydraulics," page 607).

Natural Environment Research Council. 1975. Flood Studies Report. Vol. III: Flood Routing Studies, London, England.

Ponce, V. M. y D. B. Simons. 1977. Shallow wave propagation in open channel flow. Journal of Hydraulic Engineering, ASCE, 103(12), 1461-1476. En Español: Propagaci�n de ondas poco profundas en canales abiertos.

Ponce, V. N., y D. Windingland. 1985. Kinematic shock: Sensitivity analysis. Journal of Hydraulic Engineering, ASCE, 111(4), April, 600-611. En Español: Choque cinem�tico: An�lisis de sensibilidad.

Ponce, V. M. 1986. Diffusion wave modeling of catchment dynamics. Journal of Hydraulic Engineering, 112(8), August, 716-727. En Español: Modelado de la din�mica de cuencas utilizando la onda difusiva.

Ponce, V. M. 1991a. The kinematic wave controversy. Journal of Hydraulic Engineering, 117(4), April, 511-525. En Español: La controversia de la onda cinemática.

Ponce, V. M. 1991b. New perspective on the Vedernikov number. Water Resources Research, 27(7), July, 1777-1779. En Español: Nueva perspectiva del número de Vedernikov.

Ponce, V. M. 1992. Kinematic wave modeling: Where do we go from here? International Symposium on Hydrology of Mountainous Areas, Shimla, India, May 28-30. En Español: Modelado de onda cinem�tica: �Hacia d�nde vamos desde aqu�?.

Ponce, V. M. 2014. Engineering Hydrology: Principles y Practices. Online textbook.
https://ponce.sdsu.edu/enghydro/index.html

Ponce, V. M. 2023a. When is the diffusion wave applicable? Online publication.

Ponce, V. M. 2023b. Why is the Muskingum-Cunge the best flood routing method? Online publication.

Seddon, J. A. 1900. River Hydraulics. Transactions, American Society of Civil Engineers, Vol. XLIII, 179-243, June; Extract: pages 218-223.

U.S. Army Corps of Engineers. 2024. HEC-HMS Technical Reference Manual: Synopsis of Program Methods.
https://www.hec.usace.army.mil/confluence/hmsdocs/hmstrm/program-components/synopsis-of-program-methods>

Wooding, J. 1965. "A Hydraulic Model for the Catchment-stream Problem, I. Kinematic Wave Theory," Journal of Hydrology, Vol. 3, Nos. 3/4, 254-267.

240518